广义一维势热声发动机微循环的性能分析

鄂青，吴锋，雷霆

(1.武汉工程大学光电信息与能源工程学院，湖北武汉，430205；2.武汉工程大学热科学与动力工程研究所，湖北武汉，430205)

有限时间热力学(finite time thermodynamics，FTT)[1−5]作为经典热力学的延伸，主要研究非平衡系统中能量流和熵流的规律。在低温系统和微纳米能量转换装置的进一步研究和工程实践中[6−7]，系统的量子特性变得越来越重要。在有限时间热力学与量子热力学的基础上，人们建立并分析了不同种类的量子能量转换系统，这代表了热力学的一个重要的发展方向。

人们在研究量子卡诺[8]、奥托[9]、斯特林[10−11]、迪塞尔[12]和热声[13]循环时，将其工质视为一系列粒子的集合。这些粒子有的是囚禁于一个一维无限深势阱的，也可以是被囚禁于谐振势或者四次势的，甚至可以是箱势中的极端相对论粒子[8−17]。王建辉等[18−19]验证了循环性能计算中粒子的能量谱简化式，并据此得出了广义量子奥托循环的效率及做功量的表达式。本文作者进一步对由2个等压过程和2 个等熵过程组成的热声发动机微循环展开分析。

1 广义量子热声发动机微循环模型的建立

1.1 系统的量子力学基础

普朗克的量子理论给出了粒子的能量表达式为εn=nℏω。可将处于1个广义一维势场内的粒子所具有的能量谱公式简化[18]为

式中：εn为粒子的能量；ℏ 为约化普朗克数；ω=λL-θ，是为了满足量子化的能量表达形式而构建出的频率；L为势阱宽度；λ为特定势场所固有的常数；θ和σ为由势阱种类决定的指数；n为量子数。λ，θ和σ在不同势阱条件下的取值见表1。表1中，c和m分别为粒子的速度与质量；L1为系统处于所示循环的宏观状态1时粒子所处势阱的宽度；ε1g为系统处于宏观状态1 时其中处于基态(n=1)的粒子能量。这里选用了4 种特殊势：一维无限深势阱、谐振势阱、包含相对论粒子的一维势阱以及四次势阱，它们代表了广义一维势的典型情况。系统在宏观状态i的内能εi计算式为

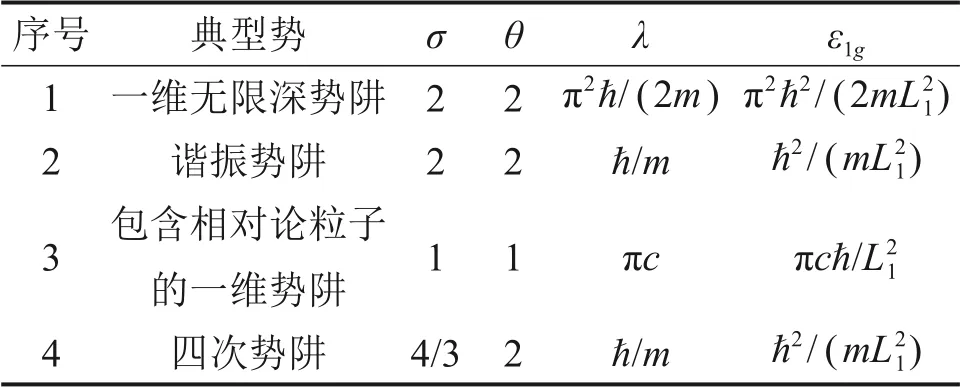
表1 不同势阱的参数比较Table 1 Comparisons of different potential parameters

式中：εin为处于状态i时n级本征态的粒子的能量；pin为状态i时处于n级本征态的粒子的概率。pin应满足如下归一化条件：

在经典热声热力过程中，外界通过振动膜片的运动对系统做功。与振动膜片的经典运动类似，可以假设广义一维势阱的壁面在有限的速度下运动，这样，当系统消耗外界功量或对外界输出功量时，其施加于势阱壁面的合力Fi就可以写为

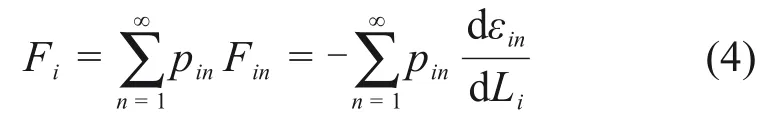
式中：Fin为处于状态i时n级本征态的粒子施加于势阱壁面的力；Li为处于状态i时的势阱宽度。

将式(1)代入式(4)可得

1.2 理想广义量子热声发动机微循环

图1所示为在理想情况下，热声回热器间气体微团与固体工质的热作用微循环过程。其中，热声板叠两端存在明显的温度梯度，板间距小于或等于气体工质热渗透深度的2倍[20]。设Tx为气团在平衡位置处的平均温度(下标x表示微团的当地坐标)，Tm为温度幅值，p0为系统静压，pm为压力波动幅值，ξm为振荡的位移幅值，dTx/dx为热声回热器固体壁的纵向温度梯度，T′i为气团处于状态i(i=1，3)时的温度与平均温度偏差的绝对值。当气体微团处于最右端状态1 时，气团的温度Tx+T′1低于与之相接触的器壁温度为Tx+ξm(dTx/dx)，因而有热量Q1从固体壁面流向气团使其温度升高，变为Tx+Tm，并因膨胀而对邻近气团做功。这一过程可近似为定压吸热过程，即图1中的过程1—2。当气团由于振荡和热弛豫快速从右端向左端运动时，此气团无法与器壁进行热交换，因而可近似认为该过程是绝热的。当气团到达左端时，温度变为Tx-T′3，压力从右端的p0+pm变为p0−pm，与气团相接触的当地壁温为Tx-ξm(dTx/dx)，气团由于膨胀而对邻近气团做功，这就是图1中的过程2—3。当气团到达左端时，由于气团温度比当地壁温高，因而有热量Q2流出气团，使其温度降低为Tx−Tm，并因被压缩而消耗邻近气团的功。这一过程可近似为定压放热过程，即图1中的过程3—4。图1(b)中的过程4—1 为近似的绝热压缩过程，当气团因振荡而从左端向右端快速运动时，由于热弛豫，它无法与器壁交换热量。当到达右端时，气团的温度变为Tx+T′1，压力变为p0+pm，此时，气团的状态回复到初始状态，完成了1个热力学循环。根据循环命名传统，可将热声发动机微循环简称为热声微循环。由热力学第一定律可知，在循环的每个过程中，气体微团作为闭口系统应满足能量守恒方程Q=Δε+W(其中，Q和W分别为在任意过程中热力系与外界交换的热量与功，ε为系统内能)。当系统自外界吸热时，Q>0；当向外界放热时，Q<0；当系统消耗外功时，W<0；对外界做功时，W>0。

图1 理想热声发动机微循环示意图Fig.1 Schematic diagrams of ideal thermoacoustic engine micro-cycle

本文从量子力学的角度分析，可将上述气体微团视为1种被限制在广义一维势阱中的粒子。为了简单，在分析量子热声微循环的过程中，只考虑由出现概率较高的2个特征态粒子构成的二能级系统。1台真正的发动机中的工作介质是由无数这样的粒子组成的。从粒子的量子行为角度分析，每个微循环都可归纳为由2个量子绝热过程和2个量子等压过程环绕而成，由此得到本文的主要研究对象即理想广义量子热声微循环(Ideal generalized quantum thermoacoustic micro-cycle,IGQTAC)，如图2所示。

图2 理想广义量子热声微循环示意图Fig.2 Schematic diagram of ideal generalized quantum thermoacoustic micro-cycle

在过程1—2中，系统与1个功源及1个高温热源(温度为TH)相偶联。随势阱壁外推，系统在相同作用力下膨胀，此时，它会从高温热源吸收大量热量，同时向功源输出体积功。通常势阱壁的运动耗时比高温热源的量子弛豫时间(约ℏ/E)长得多，即系统能够保持与高温热源的充分热接触，以确保其始终处于热平衡状态。在系统中，处于激发态(n=2)的粒子的占有概率pie与处于基态(n=1)的粒子的占有概率pig=1−pie之间应满足玻尔兹曼分布规律：

式中：k为玻尔兹曼常数；Ti为系统平衡温度。

由式(6)可求得系统处于激发态的概率为

由式(7)可得

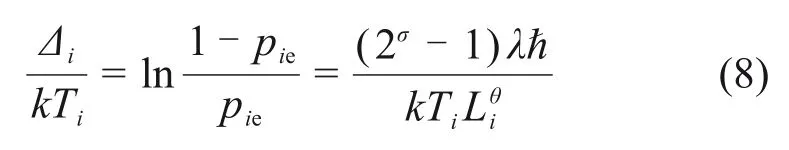
联立式(1)，(3)和(5)可得出在此过程中系统做功W12的计算式为

由于系统始终处于热平衡状态，所以，气团从高温热源的吸收的热量Q12为

式中：εi(i=1，2)为图2所示状态1 和状态2 的系统内能。由式(1)～(3)可得

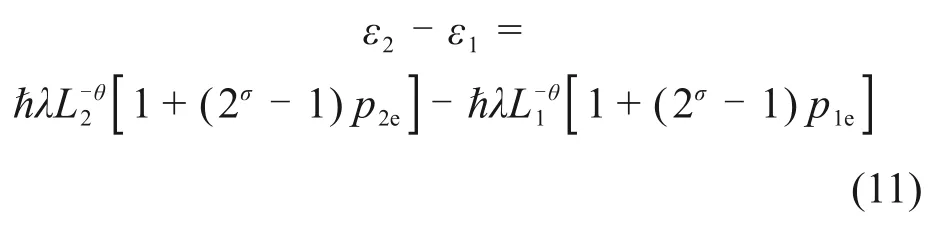
将式(9)和式(11)代入式(10)可得

在过程2—3 中，系统与外界没有热交换，系统对外界做的功将全部来自系统自身内能。在量子绝热过程中，系统内部粒子不会发生能级跃迁，即各能级粒子的占有概率维持不变，即p2e=p3e。由式(1)～(3)和式(5)可得交换的功W23为

在过程3—4 中，系统在等作用力状态下向低温热源(温度为TL)释放热量。同时，气团自身体积随势阱壁的内移被压缩，从而消耗外界功。采用类似过程1—2 的分析方法可得此过程中交换的功W34和热量Q34分别为：

在过程4—1 中，由系统绝热压缩有p4e=p1e，故消耗的功W41为

根据热力学第一定律，在理想广义量子热声微循环过程中，系统从高温热源吸收的热量QH为

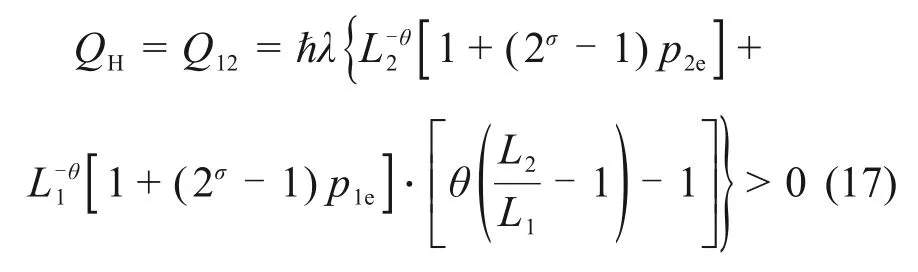
系统输出净功Wnet为

1.3 循环周期

为了计算完整的循环周期，可假设势阱宽度变化的平均速度为vˉ，这里，势阱宽度的平均变化速度很慢，因此其变化时间远大于系统及热源的弛豫时间(约为ℏ/E)，从而使系统能够始终处于热平衡状态下。则系统经历循环过程1—2—3—4—1所需的时间，即循环周期τ[21]为

1.4 循环性能参数

由式(1)～(3)可得1个二能级系统的内能ε为

由式(5)可知：1个二能级系统施加在势阱壁上的力F可写为

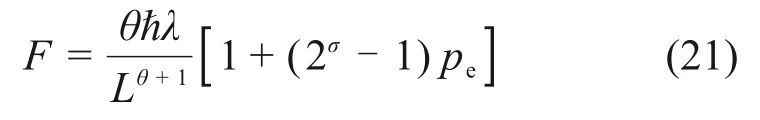
由F1=F2和F3=F4，可得

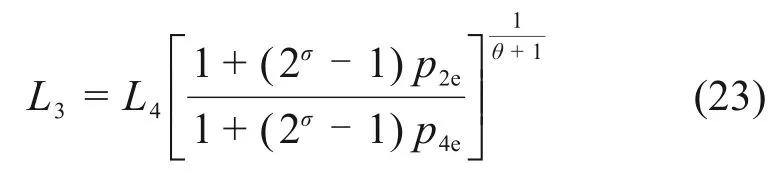
由式(7)可知当系统处在宏观状态2 和状态4时，其内部激发态粒子的占有概率分别为：

式中：y′=L2/L4>1，为势阱宽度比；T2和T4分别为状态点2和状态点4的系统温度。

在理想情况下，可取状态点4和状态点2的温度分别为冷、热端温度(图2)，即

显然，对于特定势场，p4e=p1e，它们是由L4，Tx，Tm及λ决定的。对于p4e，σ以及θ已给定的情况，p2e=p3e仅由y′决定，因此，y′是1个重要的控制参数。

将式(22)和式(23)代入式(17)和式(18)可将循环从高温热源获得的热量及做功计算式改写为：

即可得出广义量子热声微循环的效率η为

将式(22)和式(23)代入式(19)得

循环的输出功率为

对于任意特定的势场，σ和θ都是常数。当冷热端温度T4和T2已知时，由式(25)可知，式(26)和式(28)所描述的效率与量纲一功率都仅仅是p4e和势阱宽度比y′的函数。

2 广义量子热声微循环性能分析

式(26)和式(28)指出了广义量子热声微循环的性能与系统参数间的关系，在给定了一部分参数的情况下，可用图线的形式对其性能与重要参数间的关系进行研究。

对于工作介质气体微团被束缚于各种一维势阱(如一维无限深势阱、包含相对论粒子的一维势阱、谐振势阱、四次势阱等)中的量子热声微循环，可统称为一维量子热声微循环(1D quantum thermoacoustic cycle,1DQTAC)，即一维量子热声微循环包括工作于一维无限深势阱的量子热声微循环(1D infinite potential quantum thermoacoustic cycle,1DIQTAC)、相对论粒子系统量子热声微循环 (relativistic particles quantum thermoacoustic cycle,RQTAC)、谐振系统量子热声微循环(harmonic potential quantum thermoacoustic cycle,HQTAC)和四次势系统量子热声微循环(quartic potential quantum thermoacoustic cycle,QQTAC)。

由表1可见：一维无限深势阱系统与谐振系统具有相同的θ和σ，但λ与基态能量本征值ε1g是有差别的，因此，当L4和T4给定时，这2种系统唯一的区别在于具有不同的p4e。又由式(7)可推得ln(1/p1D4e- 1)/ln(1/phar4e- 1)=π2/2，其中p1D4e(phar4e)为图2中宏观状态4 时一维无限深势阱系统(谐振系统)中激发态粒子的占有概率。换言之，当一维无限深势阱系统和谐振系统的p4e相同时，由式(26)和式(28)可知，这2类量子热声微循环的性能也相同。因此，下面的分析中合并考虑这2种情况。为了便于比较，在对各种不同势场系统进行分析时，采用以下条件：Tx=600 K，Tm/Tx=0.1。

由式(26)可绘出图3所示的粒子在特定量子力学势场中运动时的热声微循环效率η与p4e及y′之间的关系曲面。由图3可见：当p4e给定时，η会随y′的增大呈单调递增的变化；而当y′取值较大时，3种不同系统的η都会随p4e的取值变化而出现较明显的变化；但当y′不断减小时，p4e对η的影响会变得非常微弱。y′在任意取值下，由∂η/∂p4e=0可求出ηmax和ηmin，此时对应的p4e分别为p4emaxη和p4eminη。由图3可见：在相同参数条件下，相对论粒子系统中的ηmax和ηmin明显比谐振系统的低；而谐振系统中的ηmax和ηmin比四次势系统的略高，即粒子处于谐振势中时，热声发动机效率较高。

图3 η与p4e及y′的关系Fig.3 Relationship among η,p4e and y′

由式(28)可绘出图4所示的气体微团在特定势场中运动时的P*与p4e及y′之间的关系曲面。由图4可见：当p4e一定时，P*与y′呈类抛物线关系；而当y′一定时，P*与p4e亦呈类抛物线关系；并且P*−y′曲线及P*−p4e曲线对于3 种势场条件都具有相似的形状；此外，存在最大值P*max以及相应的参数值p4emaxP*和y′maxP*(可根据2 个极值条件方程∂P*/∂y′=0，∂P*/∂p4e=0 联立得出)。在相同参数下，谐振系统的输出功率远比四次势系统的高；而四次势系统的输出功率又比相对论粒子系统的略高，即粒子处于谐振势中时热声发动机输出功率较高。此外，由于热声发动机的目的是对外输出有效功量，因此，若要保证P*≥0，则p4e的取值应满足0.5≤p4e≤1。

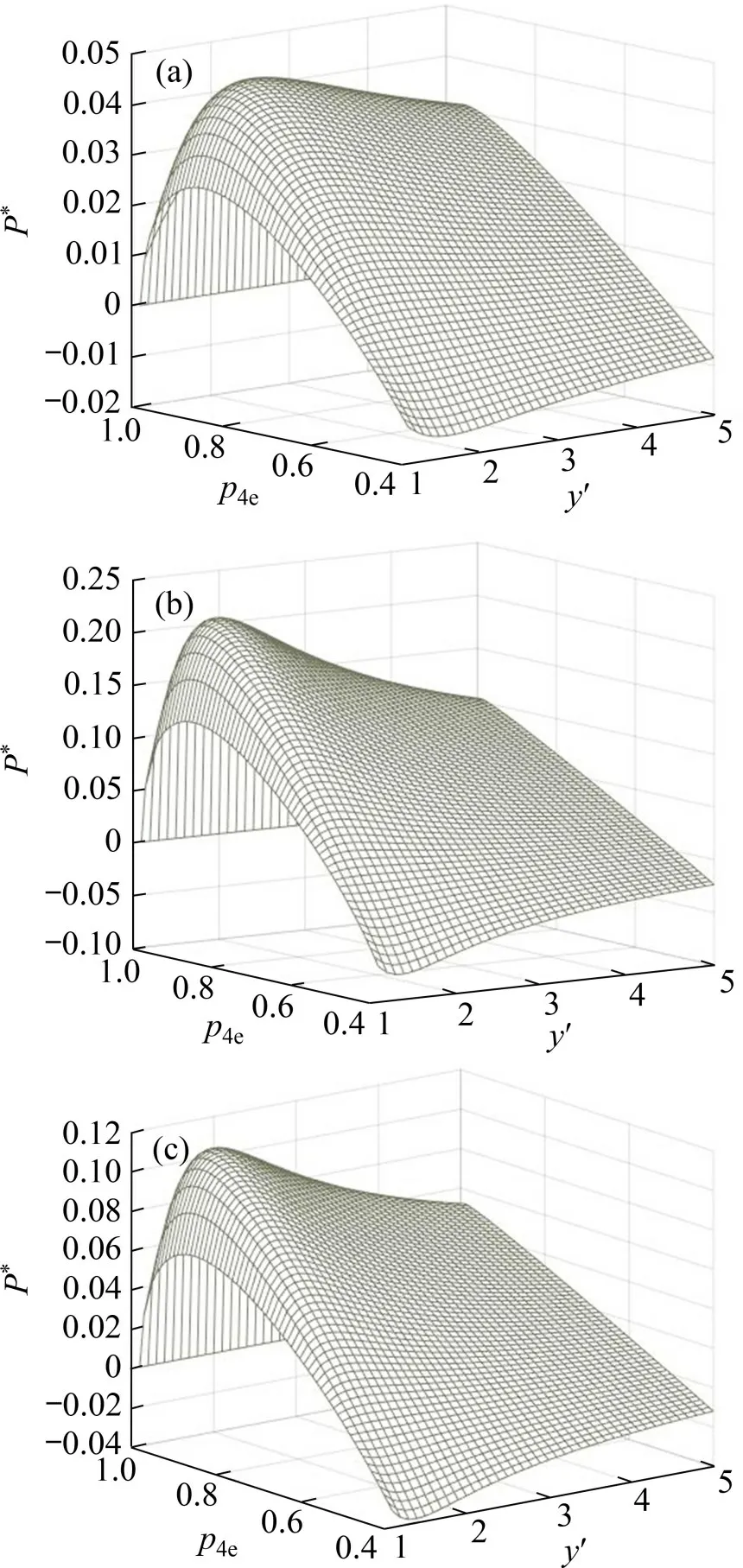
图4 P*与p4e及y′的关系Fig.4 Relationship among P*,p4e and y′

图5所示为p4e取不同数值时P*与η之间的关系。由图5可知：在3 种情况下，同一η所对应的P*会先随p4e增加而增大，达到极限p4emaxP*后继续增大p4e反而会使P*下降；在相同参数下，3种系统中循环的输出功率最大值满足P*Hmax>P*Qmax>P*Rmax，其中下标H，R及Q分别代表谐振系统、相对论粒子系统和四次势系统；且3种系统中对应于P*max的η虽然很接近但依然满足ηHmaxP*>ηQmaxP*>ηRmaxP*。可见，当粒子气体微团在谐振势中工作时，循环的输出功率与循环效率均比其他2种势场系统的高。

图5 P*与η的关系Fig.5 Relationship between P*and η

3 结论

1)当p4e给定时，工作于一维无限深势阱的量子热声微循环与工作于谐振势的量子热声微循环的性能是相同的。而当L4和T4给定时，这2种系统中的p4e会因为λ不同而不同。

2)当p4e给定时，3种势场条件下循环的η都会随y′的增大呈单调递增趋势；而当y′给定时，3 种势场条件下循环的η都会随p4e的变化而分别达到最大值ηmax和最小值ηmin。通常，ηmax出现在p4e>0.5 的区间中，而ηmin出现在p4e<0.5的区间。在相同参数下，处于3种不同势场的量子热声微循环满足ηH>ηQ>ηR。

3)当p4e一定时，P*与y′呈类抛物线关系；而当y′一定时，P*与p4e亦呈类抛物线关系；P*−y′曲线及P*−p4e曲线对于3 种势场条件下的微循环都具有相似的形状。在相同参数下，处于3种不同势场的量子热声微循环满足P*H>P*Q>P*R，并且P*达最大值时对应的p4e大于0.5。输出功率P*达最大值时循环效率η也接近最大值，此时热机性能达最好。

4)在相同参数下，当工质粒子工作于一维无限深势阱或谐振势场时，循环的效率和输出功率均比其他2种势场系统的高。