基于贝叶斯推理的数据中心用精密空调故障软修复方法研究
2021-07-14刘志强黄振霖王加强崔燕萍仝小溪
刘志强,黄振霖,2,王加强,2,崔燕萍,仝小溪
(1.中南大学能源科学与工程学院,湖南长沙,410083;2.西安建筑科技大学西部绿色建筑国家重点实验室,陕西西安,710055)
随着信息和通信技术的进步和发展,数据中心数量显著增大。2017年,数据中心用电量约占全球总用电量的2%,预计到2024年,这一比例将达到5%[1]。由于数据中心高密度散热特性,冷却系统需要全年制冷,其能耗占数据中心总能耗30%~50%,高能耗问题已成为制约信息通信技术发展的主要问题[2]。然而,制冷设备性能下降、传感器故障等原因导致控制低效,进一步增加了15%~30% 的能耗[3]。精密空调(precision air conditioner)作为数据中心冷却系统最重要的设备之一,在保证信息通信设备高效、安全运行的同时也消耗了大量的能源[2],占冷却系统能耗的40%左右。传感器故障不仅影响精密空调设备自身的运行,而且会干扰其他设备和系统的正常运行。例如,当空调末端送风温度传感器的测量值偏低时,会导致送风机转速减小、制冷量不足,造成服务器过热而“宕机”;与此同时,回水温度增高导致冷水机组频率增加,造成不必要的能源浪费。识别并移除精密空调的故障对系统节能、延长设备寿命和提高信息通信设备运行安全具有至关重要的作用。近年来,故障检测和诊断技术(fault detection and diagnosis,FDD)在暖通空调领域得到了广泛关注和发展[4−7]。WANG等[8]提出了基于主成分分析方法以检测和诊断空气处理机组故障。HAN等[9]采用了一种支持向量机与多标签技术相结合的策略,用于冷水机组故障检测和诊断。ZHAO等[10−11]提出了基于贝叶斯网络的方法以诊断空气处理机组故障。现有方法虽然能够成功地检测故障的状态并识别故障的具体类型,但故障的修复方法仍需要进一步研究[12]。另一方面,从故障的研究对象来看,人们对于数据中心用精密空调故障的少有研究。为此,本文作者综合考虑数据中心用精密空调传感器及部件的故障特征,提出一种基于贝叶斯推理的故障软修复方法。贝叶斯推理作为一种统计方法,可以利用少数现场测量数据和先验知识推导出待校正参数的后验分布,在建筑能量模型不确定性校正领域备受关注[13−14]。本文通过构建精密空调故障软修复的目标函数,将故障修复问题转化成贝叶斯推理的后验分布求解问题。当故障修复的目标函数中各项基准函数和校正函数的差值趋近于0 时,后验分布均值为故障修复值,从而实现故障软修复。
1 方法
本文采用贝叶斯推理来解决精密空调的故障软修复问题,通过目标函数来表示偏差,将目标函数引入到贝叶斯推理的似然函数中,待研究参数的目标函数可以设定为空调系统或该参数的基准输出与校正输出之间的差值。当目标函数最小即似然函数最大时,求解待研究参数的偏差。随后,将求解的偏差引入故障参数的校正函数中,实现故障软修复。
贝叶斯推理的目的是推导出一组值,使待校正参数的修正值与待校正参数真实值之间尽可能匹配。贝叶斯推理故障软修复方法的流程如图1所示。待校正参数x的后验分布P(x|Y)由全概率函数P(Y)、先验分布π(x)和似然函数P(Y|x)共同定义,其基本数学表达如式(1)~(3)所示。基于中心极限定理[15],设定每个待校正参数的先验分布π(x)服从正态分布。全概率函数P(Y)是一个标准化常数,似然函数P(Y|x)通常设定为均值为零的正态分布概率密度函数。式(3)中目标函数D(x)表示基准函数与校正函数之间的差值。

图1 贝叶斯推理耦合马尔科夫链蒙特卡罗算法流程Fig.1 Flow diagram of Bayesian Inference coupling with Markov chain Monte Carlo algorithm


式中:x为待校正参数;Y为观测值;P(x|Y)为后验分布函数;P(Y)为全概率函数;P(Y|x)为似然函数;π(x)为先验分布函数;σ为标准差;D(x)为目标函数。
为避免求解全概率函数P(Y)过程中的复杂积分问题,本文采用马尔科夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法[16−17]生成待校正参数后验分布的等效样本,从而获得待校正参数后验分布的均值、标准差等统计特征。通常,马尔科夫链蒙特卡罗算法的步骤如下。
步骤1:选择马尔科夫链的初始参数X1。初始参数由待校正参数先验分布的均值组成。
步骤2:假设概率密度函数f(Xt*|Xt-1)采用高斯概率密度函数,中心为上一个采样参数Xt-1,协方差矩阵为待校正参数先验分布的标准差。在第t步迭代中,从假设的概率密度函数中选择候选参数Xt*,候选参数Xt*通过在上一个参数Xt-1中添加1个随机变量ε得到:

式中:g为随机变量。
步骤3:根据式(5),计算候选参数的接受率α。

式中:P(Xt*|Y)为候选参数Xt*的后验分布函数;P(Xt-1|Y)为上一个参数Xt-1的后验分布函数;f(Xt-1|Xt*)表示中心为Xt*的高斯概率密度函数;f(Xt*|Xt-1)表示中心为Xt-1的高斯概率密度函数。
步骤4:根据接受率α判断是否接受新的参数。在每次迭代中,比较接受率α与随机数δ,随机数δ在[0,1]中随机生成。若接受率α大于等于随机数δ,则在第t次迭代中接受新的参数Xt*,否则,参数仍为Xt-1。
步骤5:重复步骤2 到步骤4,直到规定的采样设定值Nmcmc为止,得到后验分布的等效样本。
步骤6:对参数样本进行统计,得到待校正参数的统计特征,包括均值和标准差等。
2 仿真研究
2.1 数据中心用精密空调模型
典型的数据中心用精密空调由冷却盘管、送风风机、调节阀、空调区域等组成,主要的测量仪器为供回水温度传感器和送回风温度传感器。受工作环境的影响,温度传感器测量可能会存在一定偏差。另外,空气和水在冷却盘管表面不断流动换热的过程会造成盘管表面产生结垢。传感器的测量偏差和冷却盘管结垢问题会导致机房服务器处于高温的工作环境、增加不必要能耗等问题。为此,本文提出一种基于贝叶斯推理方法用于精密空调温度传感器及冷却盘管结垢故障的软修复研究。基于文献[18],该精密空调详细的技术参数如表1所示。

表1 精密空调的技术参数Table 1 Technical parameters of precision air conditioner
2.2 目标函数定义
基于贝叶斯理论,故障软修复的问题通过目标函数来驱动。对于应用在数据中心的精密空调传感器测量偏差及冷却盘管结垢的修复问题,目标函数包含传感器项和冷却盘管项的基准函数和校正函数,其数学表达式为

式中:和分别为传感器基准函数和校正函数;和分别为冷却盘管基准函数和校正函数;N和n分别为数据集的数量和序号;i为传感器序号。
在传感器项,基于能量守恒定律(见式(7)),传感器基准函数由其他传感器测量值及它们的补偿常数(偏移常数)组成。例如,供水温度传感器的基准函数的设定如式(8)所示。传感器校正函数由传感器自身测量值和偏移常数组成,如式(9)所示。

式中:t1,t2,t3和t4分别为供水、回水、送风和回风温度传感器温度测量值,℃;x1,x2,x3和x4分别为供水、回水、送风和回风温度传感器偏移常数,即温度传感器测量偏差,℃;ca为空气的比热容,kJ/(kg·℃);cw为水的比热容,kJ/(kg·℃);Ma,rated为额定送风量,m3/h;Mw,rated为冷水额定水流量,m3/h;f为传感器的基准函数;I为传感器数量。
在冷却盘管项,冷却盘管污垢状态下的结垢程度难以直接测定[19]。虚拟传感方法基于简单的物理传感器和数学模型可以开发一系列特定的虚拟传感器[20−22],用于评估部件的实际性能,避免了由于非连续性或周期性的手动调试而带来的设备停运时间增加及运维成本增加的问题。基于虚拟传感方法建立冷却盘管结垢虚拟传感器,表征其结垢程度。
冷水侧和冷却盘管侧的能量守恒方程为:

式中:Mw为冷冻水流量,m3/h;Δtw为供回水温差,℃;UAfault为冷却盘管污垢状态下的传热系数,kW/K;Δtm为对数平均温差,℃;ΔtA为送风温度和供水温度的差值,℃;ΔtB为回风温度和回水温度的差值,℃。
基于式(10)和式(11),得到冷冻水流量Mw:

将式(12)作为冷却盘管结垢虚拟传感器的表征量,则冷却盘管项的基准函数和校正函数的定义分别为

式中:xm为虚拟冷却盘管结垢传感器偏移常数。
2.3 先验分布定义及故障场景设定
基于文献[15],温度传感器偏差和冷却盘管结垢度的先验分布设定如表2所示。

表2 传感器偏差及冷却盘管结垢度的先验分布Table 2 Prior distributions of sensor errors and fouling fault of cooling coil
按故障发生位置及数量的不同,设置6种故障场景,见表3。

表3 故障场景设定Table 3 Settings of fault scenarios
3 结果与分析
3.1 单故障软修复
分别选取冷水侧供水温度传感器故障(Scenario 1)、风侧送风温度传感器故障(Scenario 2)和冷却盘管结垢故障(Scenario 3)作为单故障场景,验证本文提出的故障软修复方法在单故障场景下的有效性。图2所示为供水温度传感器t1偏差值的修复结果。由图2可见:供水温度传感器的偏差设定值为3.0 ℃,经过基于贝叶斯推理的故障软修复方法,识别出传感器t1偏差值为2.981 ℃,约等于偏差设定值,表明故障修复成功。

图2 Scenario 1 t1偏差的后验分布Fig.2 Posterior distribution of deviation value t1 of Scenario 1
图3所示为Scenario 2和Scenario 3的故障修复结果。由图3可知:当故障发生时,待校正参数先验分布均值为0,与偏差设定值相差较大;基于贝叶斯推理的故障软修复方法生成的后验分布样本分布密集,且均值约等于偏差设定值。Scenario 2中,送风温度传感器的偏差设定值为3.0 ℃,生成的后验分布均值为3.002 ℃;Scenario 3 中,冷却盘管的结垢程度为0.25,生成的后验分布均值为0.253。

图3 Scenario 2和Scenario 3的故障软修复结果Fig.3 Fault soft-repair results of Scenario 2 and Scenario 3
3 个单故障场景的软修复精度如表4所示。从表4可见:单故障发生的情况都被准确修复,其中,Scenario 1,Scenario 2 和Scenario 3 的软修复精度分别为99.37%,99.93%和99.20%。结果表明,在单故障场景下,本文提出的故障软修复方法都能够有效地识别精密空调的温度传感器测量偏差和冷却盘管结垢度。

表4 3个单故障场景的软修复精度Table 4 Soft-repair accuracy of three single fault scenarios
3.2 双故障软修复
分别选取同侧双传感器故障(Scenario 4)、异侧双传感器故障(Scenario 5)和单传感器+冷却盘管结垢故障(Scenario 6)作为双故障场景,验证本文提出的故障软修复方法在双故障场景下的有效性。Scenario 4 中供回水温度传感器测量偏差的修复结果如图4所示。从图4可见:供回水温度传感器的偏差设定值为3.000 ℃,先验分布均值设定为0,经过本文所提出的故障软修复方法后,识别出传感器t1的偏差值为2.773 ℃,传感器t2的偏差值为2.767 ℃。
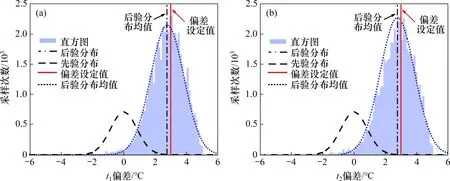
图4 Scenario 4 t1偏差和t2偏差的后验分布Fig.4 Posterior distributions of deviation values t1 and t2 of Scenario 4
图5所示为Scenario 5和Scenario 6的故障软修复结果。从图5可见:在Scenario 5 中,供水温度传感器t1的偏差设定值为3.000 ℃,回风温度传感器t4的偏差设定值为3.000 ℃;经过本文所提出的故障软修复方法后,t1偏差的后验分布均值为3.001 ℃,t4偏差的后验分布均值为2.989 ℃;Scenario 6 中,供水温度传感器t1的偏差设定值为3.000 ℃,冷却盘管设定的结垢程度为0.250;经过本文所提出的故障软修复方法后,t1偏差的后验分布均值为2.999 ℃,结垢程度的后验分布均值为0.242。

图5 Scenario 5和Scenario 6的故障软修复结果Fig.5 Fault soft-repair results of Scenario 5 and Scenario 6
表5所示为3个双故障场景的软修复精度。由表5可知:在双故障场景下,本文所提出的故障软修复方法依然具有较高的修复精度,Scenario 4 的故障软修复精度不低于92.23%,Scenario 5的故障软修复精度不低于99.63%,Scenario 6的故障软修复精度不低于96.80%。

表5 3个双故障场景的软修复精度Table 5 Soft-repair accuracy of three double-fault scenarios
由以上分析可知,无论是数据中心用精密空调同侧双传感器故障还是异侧双传感器故障或传感器+冷却盘管双故障,本文提出的故障软修复方法都能够有效地进行识别和修复。
4 结论
1)贝叶斯推理耦合马尔科夫链蒙特卡罗算法用于推导待校正参数的后验分布等效样本,避免了求解全概率函数的复杂积分问题,其中,虚拟传感方法可用于建立冷却盘管结垢度的虚拟传感器。
2)基于贝叶斯推理的故障软修复方法是一种统计的方法,该方法无需大量的数据进行训练且支持多种故障同时修复,仿真结果验证了该方法的有效性,故障软修复方法在单故障场景中的故障修复率达到99.20%以上,在双故障场景中的故障修复率也高于92.23%。
