钢管输电塔K节点承载力算法的优化研究
2021-07-14苏志钢刘海锋朱彬荣李清华
苏志钢,刘海锋,朱彬荣,李清华
(中国电力科学研究院有限公司,北京 100192)
近年来,钢管塔以其良好的受力性能在输电线路工程中得到了广泛应用,其中K形节点具有传力直接、受力性能好、加工简便、用钢量小以及经济指标优越等独特的优点,成为常用的节点形式。崔钦淑等[1]用ABAQUS对Z形柱框架节点进行仿真分析,得到等效塑性应变云图。陈继祖等[2]在分析各国规范承载力公式的基础上,考虑我国新规范设计原则、材质以及焊接条件,提出了设计承载力公式。赵必大等[3-4]建立了T形、高艳林[5]建立了十字形圆钢管-横向板相贯节点的有限元模型。陈以一等[6-7]建立了相贯节点极限承载力分析的三重屈服线模型,并建议以主管管壁塑性变形达到0.2%作为节点的极限变形。中国现行《钢结构设计规范》[8]和《架空输电线路钢管塔设计技术规定》[9]中均给出了无加劲K型相贯焊节点承载力计算方法,然而该公式的计算结果均与钢材屈服强度成线性关系,由于输电塔节点破坏是一个弹塑性稳定问题,而不仅仅是一个强度破坏的问题。因此,需要对节点承载力与钢材的屈服强度关系展开研究。
1 K节点区域内承载力计算方法
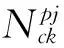
(1)
受拉支管在管节点处的承载力设计值为
(2)
式中:ψn,ψd,ψa分别为主管的轴力影响系数、支管外径与主管外径比值影响系数、两支管间隙影响系数;f为钢材的强度设计值;D,t为主管外径和壁厚;θc,θt分别为受压支管、受拉支管轴线与主管轴线的夹角。
2 K节点承载力仿真分析
2.1 节点受压承载力的加载方法
主材节点的受力简图如图1所示。图1中:F1,F2分别为支管1和支管2的轴力;θ1,θ2分别为支管1,2与主管的轴线夹角;F3为节点板的荷载;θ3为节点板对称轴与主管轴线的夹角;B为节点板长度;M,P,Q分别为节点板在底面中心所所受的弯矩、轴力和剪力。

图1 主材与斜材的连接示意图
弯矩计算式为
(3)
拉压力计算式为
P=|F1sinθ1-F2sinθ2|+F3sinθ3
(4)
剪力计算式为
Q=F1cosθ1+F2cosθ2+F3cosθ3
(5)
各加劲板上的作用力计算式为
(6)
(7)
主斜材作用在节点板上的力可以等效为图2所示的弯矩M和剪力P。

图2 斜材受力等效图
为了保证主材轴力在弯矩施加过程中保持不变,以得到轴力为特定值时所对应的节点承载力,笔者采用了2 阶段加载方法,加载过程为
1)第1加载步,主材轴向荷载加载。在主节点6上施加轴向压力,将轴力增大至N,如图3所示。

图3 第1荷载步
此时,构件的边界条件为
节点1:Ux=0,Uy=0,Uz=0,ROTx=0,Fx=N;节点6:Uy=0,Uz=0。
其中:Ux,Uy,Uz分别为x,y和z方向的移动自由度;ROTx为x方向的转动自由度;Fx为支座反力。
主材轴向荷载加载完毕后,要保证:(1)主材轴线与节点板中线的交点处的弯矩为0,主材不会发生公式所示的压弯破坏;(2)节点板形心处的弯矩不为0,随着弯矩的增大,结构1在主材4点或5点会发生局部屈曲,导致节点破坏;(3)在6点的弯矩增大过程中,主材的轴力保持不变。
2)第2加载步,支管轴力加载。第2荷载步采用如图4所示的加载方法。
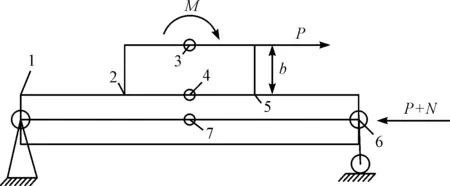
图4 第2荷载步
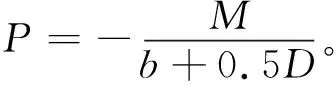
在M和P的作用下,节点4即节点板底面形心的弯矩为
(8)
在节点7处,施加在节点3处的弯矩和力P产生的弯矩相抵消,所以主材轴线上节点7处的弯矩为
M7=0
(9)
在节点6处施加力P,在受力过程中,主材的轴力始终保持N不变。因此,在第二荷载步中结构的边界条件为

2.2 节点有限元模型
采用实体单元SOLID185单元离散如图1所示的主管和插板,在主材两端横截面形心处设置节点作为主节点1和6,并将该截面上其他节点的自由度依据平截面假定凝聚在主节点上。在插板外自由面的形心处设置主节点3,利用刚性梁单元将该截面上的节点扭矩在该节点上,如图5所示。在ANSYS中,在两个荷载步中,为同一节点施加两次力会造成力的替代,而非叠加。因此,在节点6处Z方向,设置一个长度为1 mm的刚性梁单元,并将轴力施加在刚性梁单元的另一个节点上。

图5 主材-节点板的有限元模型
2.3 节点有限元仿真分析
当主材的直径D为273 mm,B为300 mm,t为6 mm,屈服强度为235 MPa时,在第1荷载步和第2荷载步,试算得到的应力云图如图6所示,TIME为节点板的弯矩载荷倍数。将主节点1的正应力沿面积进行积分后,得到的横截面弯矩、轴力等数据,结果如表1所示,其中的弯矩为节点板左侧,即图4横截面处内力对圆心积分的弯矩,预期弯矩和和预期弯曲应力为0。为了定义轴力和弯矩对结构的强度和稳定性的影响,定义等效弯曲正应力和等效轴向正应力为

表1 结构在加载过程中横截面轴力和弯矩的变化

图6 MISES应力云图
σbZ=F/A
(10)
σaZ=M/W
(11)
式中:A为钢管的横截面面积;W为钢管横截面的抵抗矩。
由表1结合图6可知:当TIME=1时,即第1个荷载步加载完毕时,主材的应力很大且分布非常均匀,而节点板的应力几乎为0;当TIME=1.2时,主材的应力很大但分布很不均匀,节点板两端的应力明显增大。因此,该现象可以说明在第1荷载步仅施加了轴力,在第2个荷载步在第1个荷载步的基础上施加了弯矩。在TIME小于1时,即在第1荷载步中,主材轴力和轴向应力随这个荷载步的增加均匀增加;在TIME大于1时主材轴力和轴向应力随这个荷载步的增加保持不变,且在整个加载过程中,主材轴力和轴向应力的预期值与有限元计算值非常接近,说明该有限元模型实现了轴力的加载目标;在加载过程中,有限元计算得到的弯矩看似与预期值相差很大,但有限元计算得到的等效弯曲应力与钢材屈服强度的比值是非常趋近于0的,根据构件压弯稳定计算公式,该弯矩对主材稳定性的影响基本为0,可见,该有限元模型实现了弯矩的加载目标。
3 K节点承载力修正
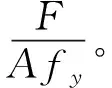

图7 弯矩峰值应力云图(TIME=1.688 8)

图8 弯矩峰值塑性应变云图(TIME=1.688 8)

表2 屈服强度与承载力的关系
由图7,8可知:在节点的受力过程中,插板上下两端和主材的交点处的应力和应变明显大于其他部位。由表2可知:节点破坏时的压弯应力均小于材料的屈服强度,没有发生压弯破坏,可见节点发生了因钢管局部承载力不足引起的破坏。
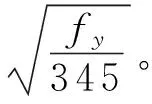
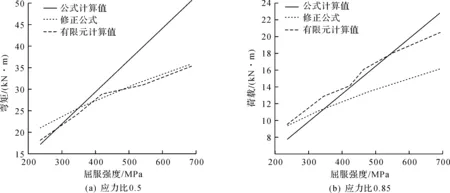
图9 屈服强度与承载力的关系
由图9可知:当节点板的荷载为35.38 kN·m时,节点板的最大位移为6.58 mm。当节点板的荷载为51.01 kN·m时,节点板的最大位移达到了31.92 mm,与直径之比达到了11%。因为确定轴压钢管稳定系数时需要假设钢管横截面是圆形的,过大的局部变形会导致钢管发生轴压或压弯破坏,所以实际钢管主材是不可能容许这么大的局部变形的。可见K节点的承载力涉及到钢管的局部稳定承载力,在轴压比较低时,有可能发生延性破坏。因此,采用最大承载力和最大变形双重控制的方法来确定它的承载力是合适的,而修正后的公式更符合有限元计算结果。
4 结 论
针对《钢结构设计规范》中K节点计算公式与屈服强度成线性关系而未考虑弹塑性稳定破坏,利用有限元仿真分析了屈服强度对节点承载力的影响,给出了K节点承载力计算的弹塑性修正系数,通过计算后与原规范公式对比,该弹塑性修正系数更符合有限元仿真结果。同时,笔者仅对管径273 mm的钢管进行了仿真分析,若要应用于工程实际还需要补充其他管径的钢管仿真分析以验证修正系数的通用性。
