匹配层高频宽带水声换能器研究

潘 晶，刘 佳，戴思思，王 艳

（上海船舶电子设备研究所，上海 201108）

0 引言

随着水声信号处理技术的快速发展，为了获取更多的水下信息，提升声呐的探测和识别效果，须使得脉冲激励下的声呐的余震信号尽量小，即机械品质因数 Qm值较低，这就要求设计制作高频宽带声呐。高频宽带换能器是高频宽带声呐信号产生和获取的基础。一方面，可以提升整个声呐系统的性能，携带更多的信息进行水下探测与识别[1-2]；另一方面在信号传输上也具有显著优势，如减少波形畸变、提高可靠性和保密性、提高系统分辨率等[3-6]。

提高换能器带宽的方法有很多种，其中匹配层技术应用较为广泛，同时也是一种行之有效的方法。采用匹配层技术，通过在换能器压电元件的辐射面添加具有一定声阻抗值的无源材料，产生双谐振或多谐振方式可以实现拓宽带宽的效果。

本文从理论数值计算和有限元仿真入手，对匹配层技术应用于拓宽换能器带宽方面进行了研究。分析制作了双匹配层水声宽带换能器，实现了换能器的宽带发射。

1 匹配层换能器的设计

1.1 匹配层的理论研究

匹配层理论实际上是利用了声波的反射和透射原理。高效率宽带换能器实现的主要困难在于压电材料（特性阻抗约35 MRayls）与水（特性阻抗约1.5 MRayls）之间的声阻抗失配，从而降低了换能器在水中的透射效率[7]。声波由压电材料垂直传递到水介质中时，由于两者的声阻抗相差较大，大部分声波在界面处被反射，只有小部分声波能够透射。通过在压电晶片的辐射端添加匹配层，能够实现压电材料的声阻抗与工作介质（例如水）之间声阻抗的过渡，有利于声能的传播。匹配层换能器在水中工作的物理结构模型如图1所示。

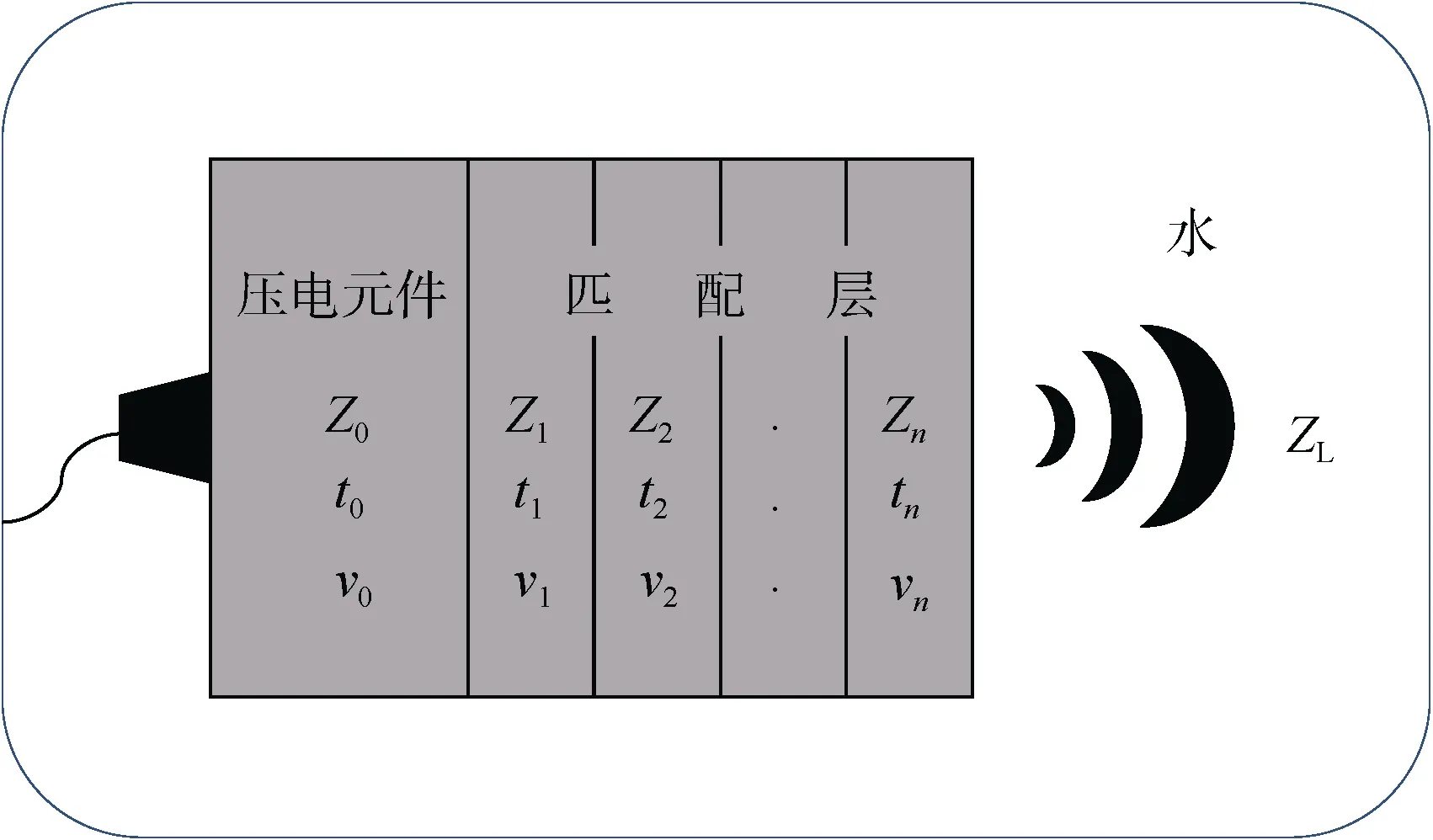
图1 多匹配层换能器水中工作的物理结构模型Fig.1 Physical structure model of multi-matching layer transducer working in water

图1中，Z0和ZL分别为压电元件和负载的特性阻抗，Z1…Zn分别为各层匹配层的特性阻抗；t0为压电元件的厚度，t1…tn分别为各层匹配层的厚度；υ0为压电元件的声速，υ1…υn分别为各层匹配层的声速。

当压电元件受到电激励时，振动产生的声波通过匹配层传播到负载中。根据Chebyshey理论[8]，实现最佳透射条件所需匹配层的特性阻抗，计算公式为

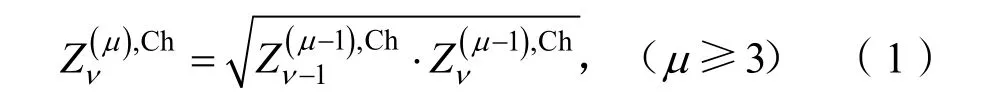
式中：μ表示媒质的层数（包括压电片和传播介质）；υ表示第υ层媒质；为含有μ层媒质的换能器中第υ层媒质的特性阻抗。

利用上述公式（1），可计算出不同层数匹配层对应的特性阻抗值。理论上来说，在不考虑声波衰减的情况下，假设所有匹配层的厚度均为匹配层材料的1/4波长，随着均匀匹配层层数的增加，声透射效率会逐渐增加，拓展带宽的效果会越好[9-11]。但是，实际中随着匹配层层数的增加，衰减会逐渐增加，所以在选择时需衡量利弊。在实际工程中，通常采用添加单层或者双层匹配层的方式来拓展换能器的带宽。

本文以实现水声换能器宽带性能为目的，考虑工艺的可操作性及普遍适用性，设计双层匹配层水声换能器。选用 PZT-4压电陶瓷作为换能材料，以水作为传播介质。为了减少压电陶瓷和水的声阻抗差异，对压电陶瓷进行切割灌注环氧树脂，制成1-3复合材料作为压电元器件。与常规的压电陶瓷相比，1-3复合材料具有较低的特性阻抗、低介电常数、高静压电常数、低机械品质因数Qm值、较小的机电耦合系数、良好的柔韧性等优点[12]。在理论计算的基础上研制了双层匹配层材料，其核心参数如表1所示。

表1 换能器材料参数Table 1 Parameters of materials for transducer

1.2 匹配层的机电等效电路计算

机电等效电路[13]是换能器研究的常用方法，它将机械振动、电振荡以及机电类比原理形象地组合在1个等效图中。将换能器作为电路的一部分进行分析，等效电路方法十分有效且简便。图2为考虑损耗的双层匹配层条件下的等效电路图，其中虚线框中的为匹配层的等效电路。

图2 双层匹配层换能器的等效电路图Fig. 2 Equivalent circuit diagram of double matching layer transducer

图2中各参数为

其中：C0为静态电容；n为机电耦合系数；Z1、Z2为压电陶瓷的等效阻抗；Zai、Zbi为第i层匹配层的等效阻抗；w、l、t0分别为压电陶瓷的宽度、长度和厚度；ti为第i层匹配层的厚度；0ρ、C0、k0为压电陶瓷密度、声速和波数；iρ、ci、ki为第i层匹配层的密度、声速和波数。考虑到介电损耗和机械损耗，上述的静态电容、机电转换系数、声速和波数均为复数，其虚部决定了衰减。

本文选用 9.6 mm高的 PZT-4压电陶瓷制成1-3复合材料作为换能元件，其空气中实测谐振峰频率为162 kHz。与压电陶瓷相比，制成的1-3复合材料降低了横向振动的强度，使得厚度振动更加纯净，并有效降低了密度和声阻抗，从而更容易与水相匹配。利用机电等效电路进行数值计算，分别计算无匹配层、单匹配层和双匹配层换能器自由振动条件下的电导，所有匹配层的厚度均为匹配层材料的1/4波长。

由图3-5可以看出，等效电路数值计算的方法下，无匹配层的压电复合材料其谐振频率为161 kHz，与复合材料实物实测结果相比误差率为0.6%，一致性较高。随着粘接匹配层的层数增加，换能器出现了多个谐振峰，这是因为当压电材料粘接匹配层后，相当于对换能器自身增加了参与振动的部件，或者说增加了负载质量，换能器的基频就会降低。由于匹配层材料的特性阻抗小于换能元件的特性阻抗，故而其高频谐振频率也会降低，这样在工作频带范围内就形成了靠近的谐振峰，从而拓展了工作频带。

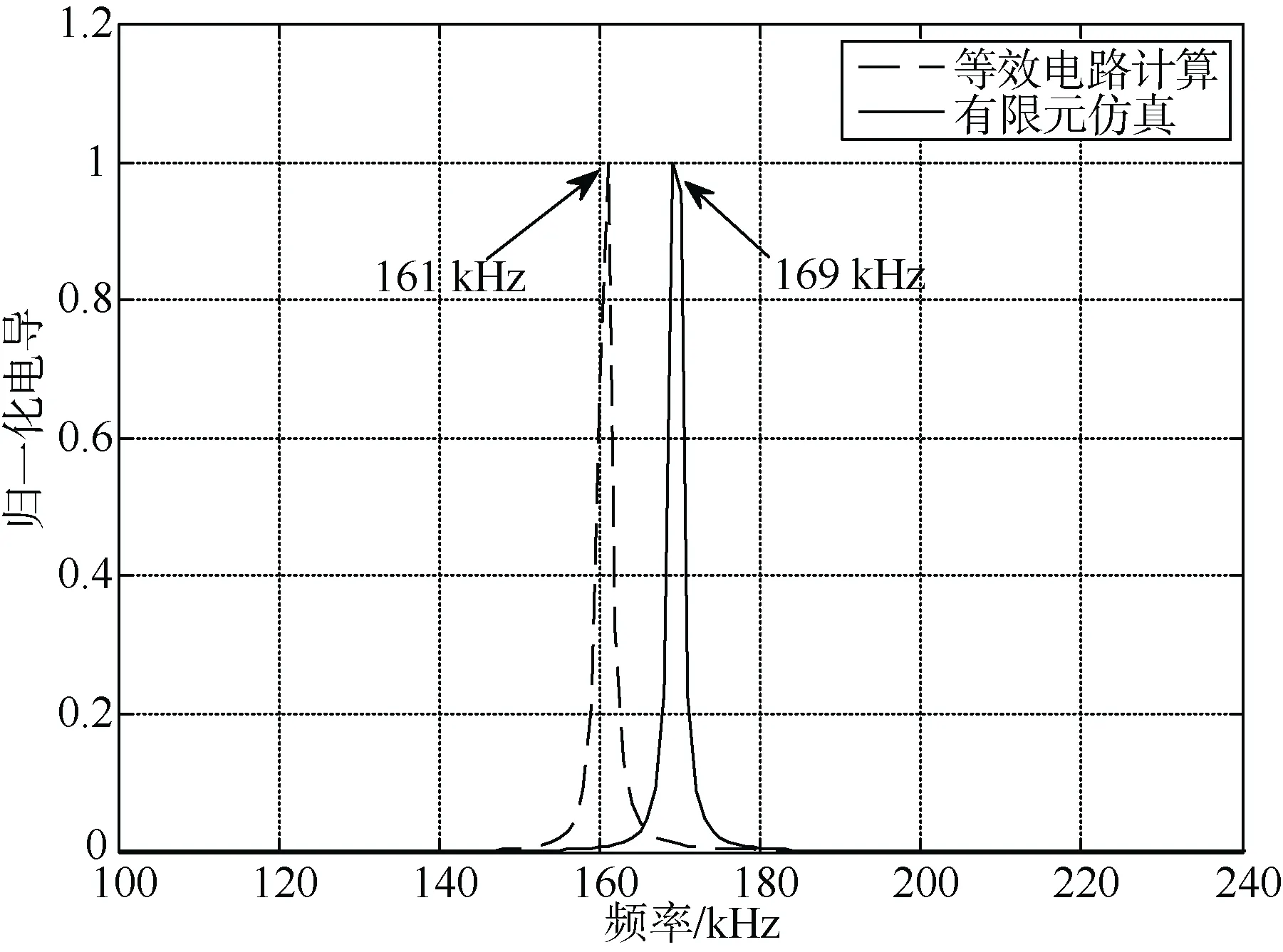
图3 空气中无匹配层换能器等效电路计算和有限元仿真电导图Fig. 3 Conductance diagram of equivalent circuit calculation and finite element simulation for the non-matching layer transducer in air

图4 空气中单匹配层换能器等效电路计算和有限元仿真电导图Fig. 4 Conductance diagram of equivalent circuit calculation and finite element simulation for the single matching layer transducer in air

1.3 匹配层的有限元仿真

采用与数值计算相同的材料参数，考虑压电陶瓷、填缝材料以及匹配层的衰减损耗，对换能器进行有限元仿真分析，研究匹配层对换能器性能的影响。由于1-3型复合材料具有周期性和对称性，因此可以通过只建立 1个周期的复合材料进行有限元仿真，以便节省计算时间，其有限元模型图见图6。图6（a）中，蓝色部分为PZT-4压电陶瓷，灰色包裹压电陶瓷的为环氧树脂，组成 1-3复合材料；图6（b）在图6（a）的 1-3复合材料上添加了1层匹配层；图6（c）添加了2层匹配层。

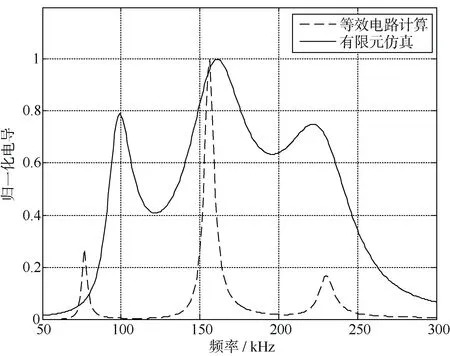
图5 空气中双匹配层换能器等效电路计算和有限元仿真电导图Fig. 5 Conductance diagram of equivalent circuit calculation and finite element simulation for the double matching layer transducer in air

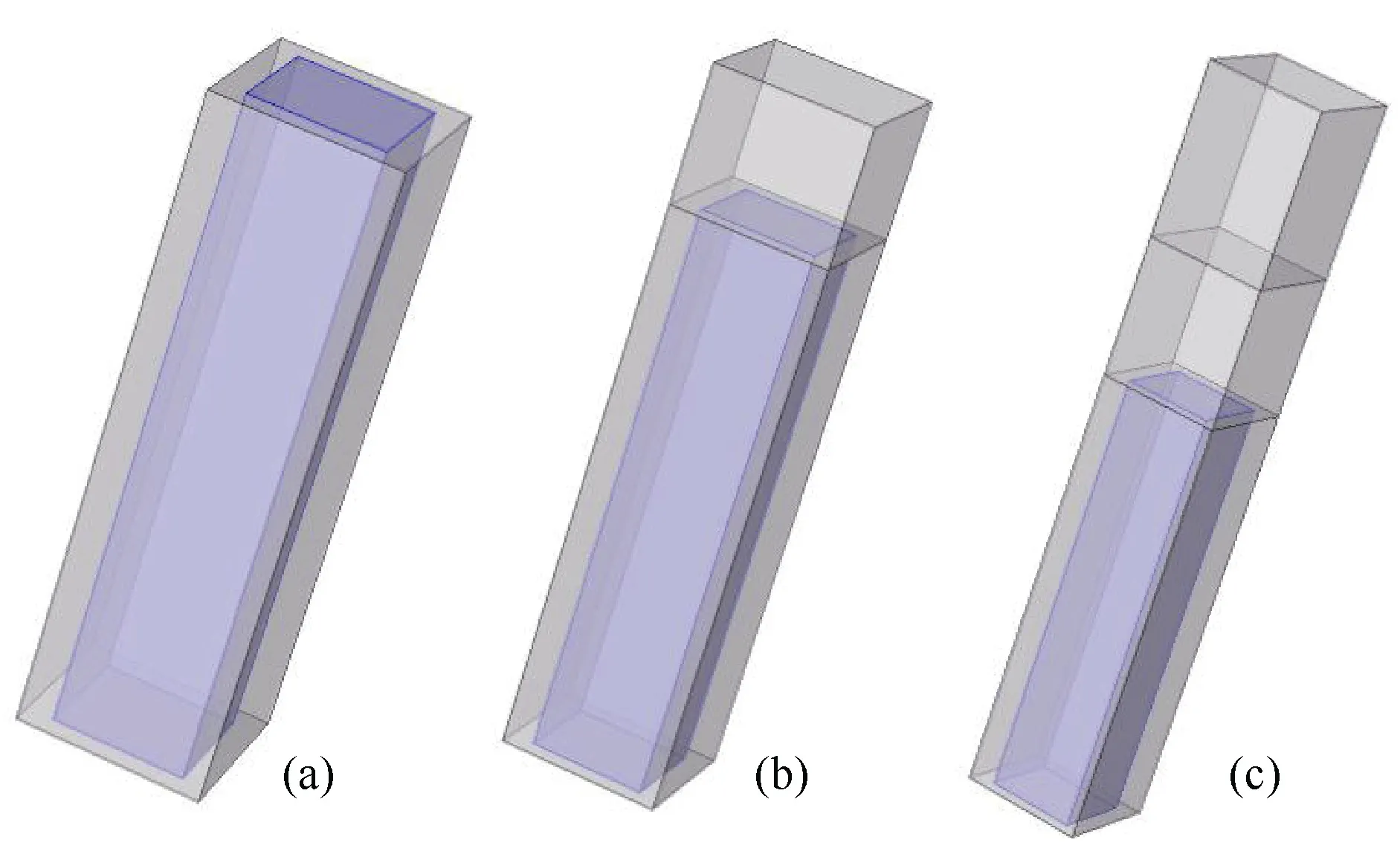
图6 无匹配层、单匹配层和双匹配层的1个周期单元的有限元模型（蓝色部分为压电陶瓷）Fig. 6 Finite element model of a periodic element for non-matching layer model，single matching layer model and double matching layer model（The blue part is piezoelectric ceramic.）

从图3-5的有限元仿真的电导图可以看出，无匹配层时仿真的谐振频率为169 kHz，相对实测误差率为0.43%，与实际较为接近。对双匹配层高频宽带换能器进行模态分析。由图5可以看出，该换能器存在3个振动模态。图7则为对应的3个谐振频率的振动模态。

图7 双匹配层高频宽带换能器的振动模态（位移/mm）Fig. 7 Vibration mode of double matching layer high frequency broadband transducer（displacement /mm）

由图 7（a）可以看出，只有 1个节点在靠近第1层匹配层与压电元件的交界处，振动位移的最大值在单周期换能器单元的两端，且相位相反，为换能器的纵向振动模态，谐振频率为100 kHz。从图 7（b）可以看出，换能器的两端以及第 1层匹配层与第2层匹配层的交界处有大的振动位移。其中，最大振动位移在靠近第1层匹配层与第2层匹配层的交界处，且节点约在压电元件与第1层匹配层整体的中间部分，为该整体的纵振动模态，谐振频率为163 kHz。从图7（c）可以看出，换能器单元有2个节点，对应着高阶纵振动模态，谐振频率为223 kHz。

对比数值计算和有限元仿真的结果，二者在无匹配层和单层匹配层的条件下虽有差异，但一致性较高。当增加的匹配层为2层时，二者出现较大差异。相比于等效电路的数值计算，有限元仿真在工作频带内形成的3个谐振峰更加靠近平稳，这可能是由于有限元仿真更真实地反映了实际的材料参数和边界条件等情况。

1.4 匹配层宽带换能器研制

为实现换能器的宽带性能，研究设计双层匹配层的水声换能器。本文利用有限元仿真，模拟换能器在水介质中的性能，调整优化换能器2层匹配层的厚度参数分别为2.5 mm和4 mm，形成多谐振峰，谐振峰之间相互耦合，形成宽带。设计出1个中心频率为 187.5 kHz、最大发送电压响应为150.3 dB、-3 dB频带范围为115～260 kHz、带宽宽度为 145 kHz的水声换能器，实现了相对带宽为77.3%的宽频带效果。其中，换能器振子的厚度、宽度和长度分别为16.2 mm、22.4 mm和42 mm，封装后如图8所示。

图8 双匹配层换能器实物图Fig. 8 Picture of double matching layer transducer

由图9-10可以看出，双层匹配层换能器在水中的有限元仿真的电导和发送电压响应与实测结果相比，二者吻合度非常高，说明有限元仿真对于匹配层换能器的研究具有良好的指导作用。

图9 水中双层匹配层换能器有限元仿真与实测电导图Fig. 9 Finite element simulation and measured conductance diagram of the double matching layer transducer in water

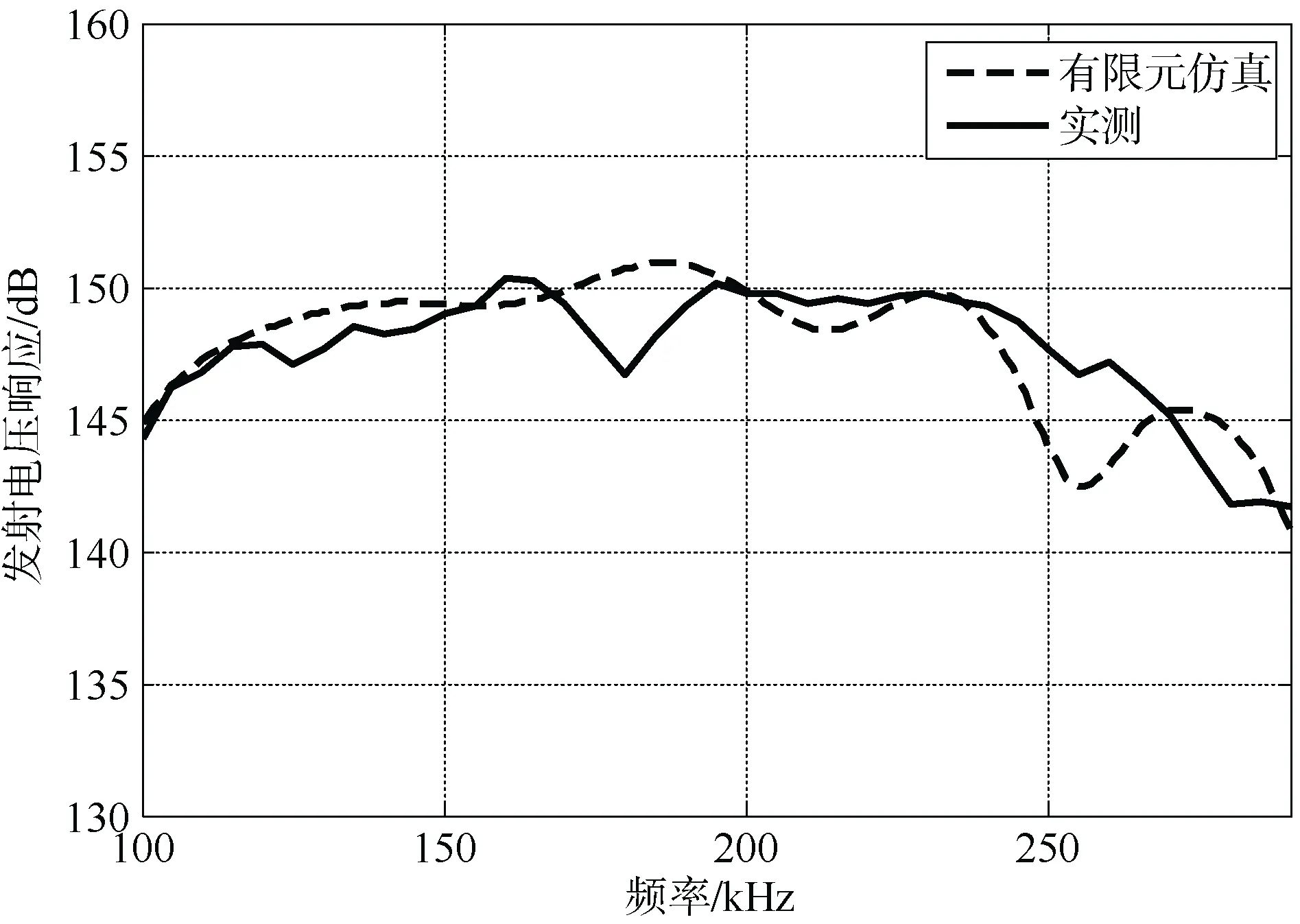
图10 水中双层匹配层换能器有限元仿真与实测发送电压响应图Fig. 10 The finite element simulation and measured emission voltage response diagram of the double matching layer transducer in water

2 结束语

本文通过对换能器拓宽带宽的有效方法——匹配层技术，进行了理论分析，得到所需双层匹配层的材料参数。利用所得的材料参数，从机电等效电路数值计算和有限元仿真入手，对比分析了无匹配层、单层匹配层和双层匹配层对换能器性能的影响。最后，利用有限元仿真，分析换能器的振动模态，优化双层匹配层的厚度参数，指导设计换能器样机并进行测试，得到的电导和发送电压响应的实际测试结果与仿真结果高度吻合。

根据数值计算和有限元仿真，设计出一款中心频率为187.5 kHz，频带范围为115～260 kHz的双层匹配层宽带水声换能器，其相对带宽为77.3%。

本文通过数值计算、有限元仿真和实验测试证明了双层匹配层拓宽换能器带宽的有效性。粘接2层匹配层后，在压电陶瓷的谐振频率两侧出现2个谐振峰。由于添加的匹配层为无源材料，且存在机械损耗，谐振峰之间靠近耦合，实现了拓宽频带的效果。利用双层均匀匹配层，换能器的带宽得到了大大的提高，且使用均匀匹配层，操作更便捷，可以满足更加广泛的工程需求。