水声时变信道下OFDM系统运动多普勒补偿
2021-07-14王婷婷王正伟王沫然何桂萍蒋洪福
王婷婷,陈 洲,王正伟,王沫然,何桂萍,蒋洪福
(四川九洲电器集团有限责任公司,四川 成都 621000)
0 引言
水声通信系统受限于水声信道特性的影响,其工作频率多为窄带,这导致了各个子载波间的载波间隔很小,抗多普勒性能较差。而且,水声频偏是非一致频偏,即对不同子载波产生的频率偏移不同,难以准确估计出每个子载波的频偏并进行多普勒补偿,多普勒估计和补偿技术是水声 OFDM通信技术的关键技术之一。多普勒估计技术主要由多普勒因子预估计和多普勒因子块估计2部分组成。传统的多普勒估计技术主要通过循环前缀、OFDM符号的持续时间以及插入的 CW(Continuous Wave)或单频序列等来估计多普勒因子[1]。这些方法对一致多普勒因子估计效果较好但是对于时变信道下的非一致多普勒因子的估计效果较差。对多普勒因子估计之后需要根据多普勒因子的大小去补偿由多普勒效应导致的子载波频移,常见的多普勒补偿方法有变采样滤波器、高分辨率 DFT(Discrete Fourier Transform)[2-3]等。此外,研究人员研究出不同的技术方法来对抗多普勒频偏,主要包括多普勒分集接收,两步多普勒补偿,基于压缩感知的信道均衡技术,分段傅里叶变换等[4]。其中,Hyungjoon Song提出的多普勒分集接收的方法来抑制载波间干扰,其主要思想是对接收信号进行人为的不同频移,通过将多路不相关信号 FFT解调后进行加权判决,进而得到更好的性能,但更多分集带来更好性能的同时也会增加算法运算的复杂度[5-6]。Ma Xuefei等人提出一种基于小波函数的 OFDM数据水下声信道多普勒失真补偿方法(WFFT),小波函数中平滑变化的多项式极大地降低了处理数据的相关性,使信道估计和均衡更加准确[7]。本文根据M. Stojanovic、S. Zhou等人提出的两步多普勒补偿技术来应对时变信道,即将宽带多普勒补偿和窄带多普勒补偿结合使用[8-10]。经验模态分解法(EMD)可以将待分析的非线性、非平稳信号分解为数个平稳信号,并按照其频率由高到低进行排列,本文将使用EMD算法配合完成宽带多普勒补偿,在粗补偿处理后,使用 WFFT算法完成窄带多普勒补偿。与WFFT单步多普勒补偿算法相比,本文使用的方法在更大的移速条件下具有较大的优势。
1 多普勒补偿算法
1.1 收发端相对运动情况下的频偏分析
假设接收端与发送端的相对运动速度表示为v,发送信号频率表示为 f0,波达方向与发射机运动的方向之间的夹角为θ,声速设定为c,那么多普勒因子可以表示为 a =v c osθ /c ,此时的多普勒频移 fd为
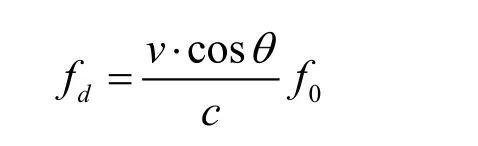
当收、发节点相对匀速运动时,即无加速度时,产生的Doppler为恒定Doppler,OFDM的每个子载波上对应非一致 Doppler。即每个子载波产生的Doppler按比例变化,产生的频偏量不一致。以1 500 Hz信号为例,图1给出了OFDM子载波产生了非一致的Doppler频偏示意图。
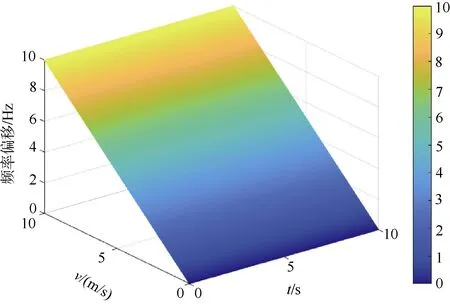
图1 OFDM子载波非一致Doppler时频图Fig. 1 Time-frequency diagram of OFDM sub-carrier non-uniform Doppler
当传输OFDM符号时,节点的速度产生变化,即有加速度情况,就会产生时变宽带 Doppler,这种 Doppler会使信号产生严重的衰落和畸变。以1 500 Hz信号为例,图2给出了OFDM子载波时变Doppler示意图。
图2是时变多普勒情况下的OFDM子载波频率变化情况,与恒定多普勒不同的是,时变多普勒对于每一个子载波在不同时间下所产生的多普勒频偏不同,且加速度越大,频偏变化越快,这对OFDM的解调造成了很大的困扰。

图2 OFDM子载波时变Doppler时频图Fig. 2 Time-frequency diagram of OFDM sub-carrier time-varying Doppler
1.2 EMD频偏估计原理
经验模态分解法(EMD)可以将待分析的数据信号分解为数个平稳信号,并按照其频率由高到低进行排列。其分解过程是按照基于数据信号时间线本身进行信号分解,没有任何固定的先验知识,也不需要建立任何基础函数。EMD算法将信号分解后会得到可以体现信号频率特征本质的有限个本征模函数(IMF,Intrinsic Mode Function)和1个剩余分量(RC,Residual Component)。EMD分解结束之后,对获得的数个有限特征函数执行希尔伯特变换(HT,Transform Hilbert),从而获取即包含时间信息又包含频域信息的希尔伯特频谱图。具有时频信息从而满足信号时间频率分析的要求。EMD分解过程如下:
1)寻找待分解信号数据序列x( t)全部的极大值点,并且通过使用3次样条插值函数进行拟合结合全部极大值点形成原始待分解数据的上包络线;
2)寻找待分解信号数据序列x( t)全部的极小值点,并且通过使用3次样条插值函数进行拟合结合全部极小值点形成原始待分解数据的下包络线;
3)计算上包络线和下包络线的均值(在实际应用中,有的研究人员将平均值改用中位值,对于非平稳时间序列此种方法也可行);
4)将待分解数据信号序列x( t)与求出的平均包络做减法,得到一个全新的数据序列;
5)用待分解数据信号减去上一步获得的新数据得到一组信号,若此信号中还存在负的局部最大值和正的局部最小值,则认为该信号并不是一个本征模函数,则需要继续进行。
假设单频信号频率为fc的余弦信号可表示为
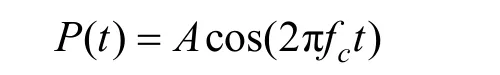
经过水声信道后,接收端接收到的信号可表示为
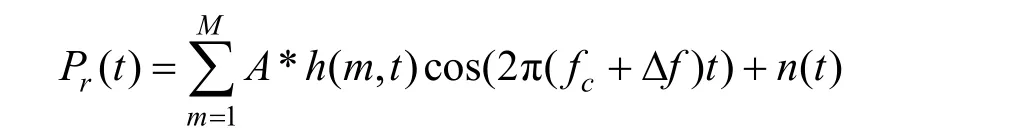
式中:M为信道多径数;h( m, t)表示第K/2个子载波的信道衰落系数;ΔfK/2为频率偏移量;n( t)是加性噪声。

式中,nc( t)和 ns( t)为噪声的同相分量和正交分量。可知,经过相干检测后即可获得含有频率分量的信号。对该信号进行EMD分解,即可观测频偏量。
对数据进行EMD分解即是为了获得函数本质频率特征,上述通信系统模型中的单通道信号首先在经过相干检测后,得到的输出信号中将会混淆有多个带频率偏移量的频率信息。之后再结合 EMD算法的频率筛选性能,就可以将混合的频率信息按照从高频到低频的流程识别出来,以此来获得被分解信号的频率信息。
1.3 基于PEMD-WFFT的多普勒补偿算法
通过上述分析可知,OFDM中心频率的信号具有相对平均的频偏。宽带多普勒补偿时可将中心频率的频偏当作 OFDM信号的频偏进行估计。本文将估计 OFDM信号中心频率点的频偏,并以此为依据进行重采样宽带多普勒补偿。具体做法是在OFDM信号前放置一段中心频率的单频信号,用来估计信号多普勒频偏。采用的信号结构如图3。
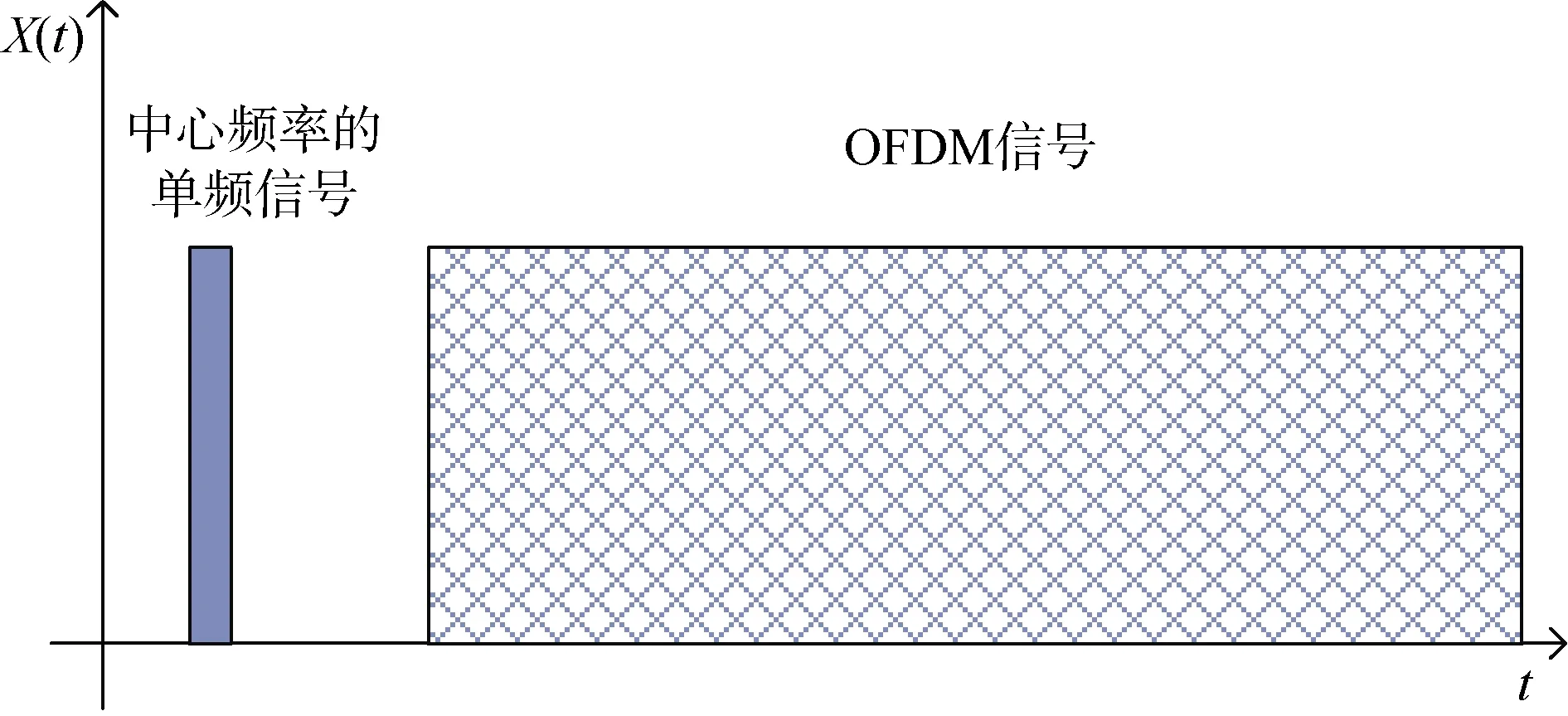
图3 信号帧结构Fig. 3 Signal frame structure
即经过串行到并行转换、编码、符号映射等调制过程的发送信号为
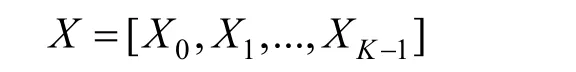
经过IFFT后变成频域信号,通过换能器传输的信号表示为

式中:K为载波数;N表示逆傅里叶变换点数;T为信号OFDM符号的持续时间跨度。
接收端接收到的信号为
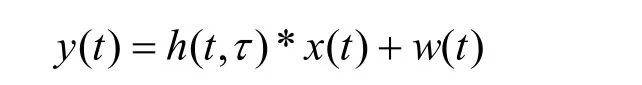
此时截取多普勒粗估计信号,该信号带有频偏信息。将通过相干检测处理后的信号输入EMD算法,分析频谱成分,进而获得频偏信息,通过重采样完成多普勒粗补。
经过下变频去掉循环前缀(CP)后,得到的信号建模为
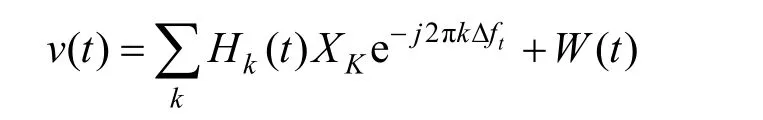
水声信道是一个时变信道,根据增益和延迟,可以建立信道函数为
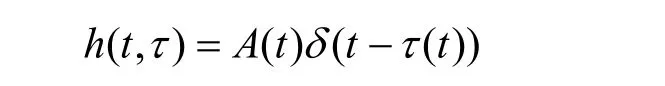
在WFFT算法中,信道被看作是时间和频率的平滑变化函数,这个平滑的变化函数可以用一组基函数来表示。根据函数逼近思想,信道函数可以使用某组基函数进行逼近,也可以理解为将信道函数分解到该组基函数上,表示为
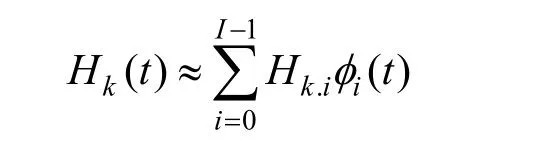
WFFT算法通过对 Morlet母波进行平移和尺度变换得到一组 Morlet小波函数,采用该组小波函数进行信道函数分解,该基函数表达式为

式中,i的最大值为一组小波函数的个数,即WFFT算法阶数。
将 WFFT算法处理后的数据输入自适应梯度算法,通过载波进行均衡,完成窄带多普勒补偿。
2 仿真结果
图 4是当收发端相对速度变化,信噪比为14 dB时的仿真结果。起始位置附近相对运动速度低,产生的多普勒偏移小,PEMD算法增益不明显。随着运动速度的增加,ICI也在增加。PEMD-WFFT算法性能逐渐优于WFFT算法。
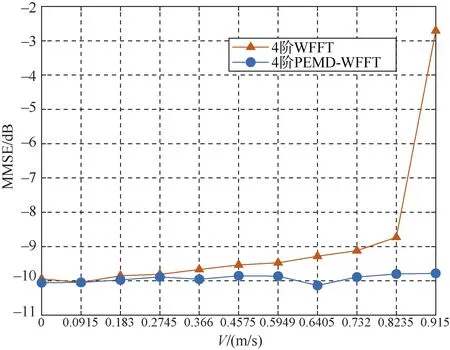
图4 相对速度为0~0.915 m/s的仿真结果Fig. 4 Simulation results at a relative speed of 0~0.915 m/s
图 5是当收发端相对速度更大,信噪比为14 dB时的仿真结果。可以看出当相对速度较大时,WFFT算法性能较差。

图5 相对速度为1.83~18.3 m/s的仿真结果Fig. 5 Simulation results at a relative speed of 1.83~18.3 m/s
图6是在不同信噪比下的仿真结果,其中相对速度为 0.183 m/s。可以看出随着信噪比的增加 2种算法的性能都在优化,且由于相对运动速度较小二者的性能差别不大。
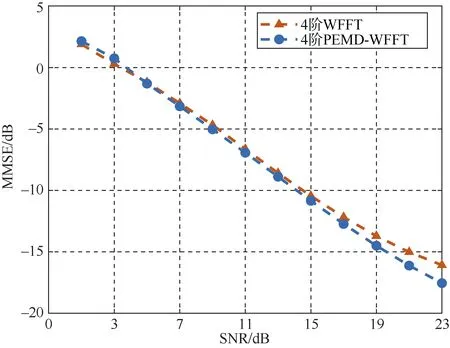
图6 相对速度0.183 m/s时信噪比变化仿真结果Fig. 6 Simulation results of the change of signal-to-noise ratio at a relative speed of 0.183 m/s
图7是在不同信噪比下的仿真结果,其中相对速度为7.32 m/s。在此仿真条件下,WFFT算法几乎不收敛。随着信噪比的增加,PEMD-WFFT算法的性能逐渐优化。
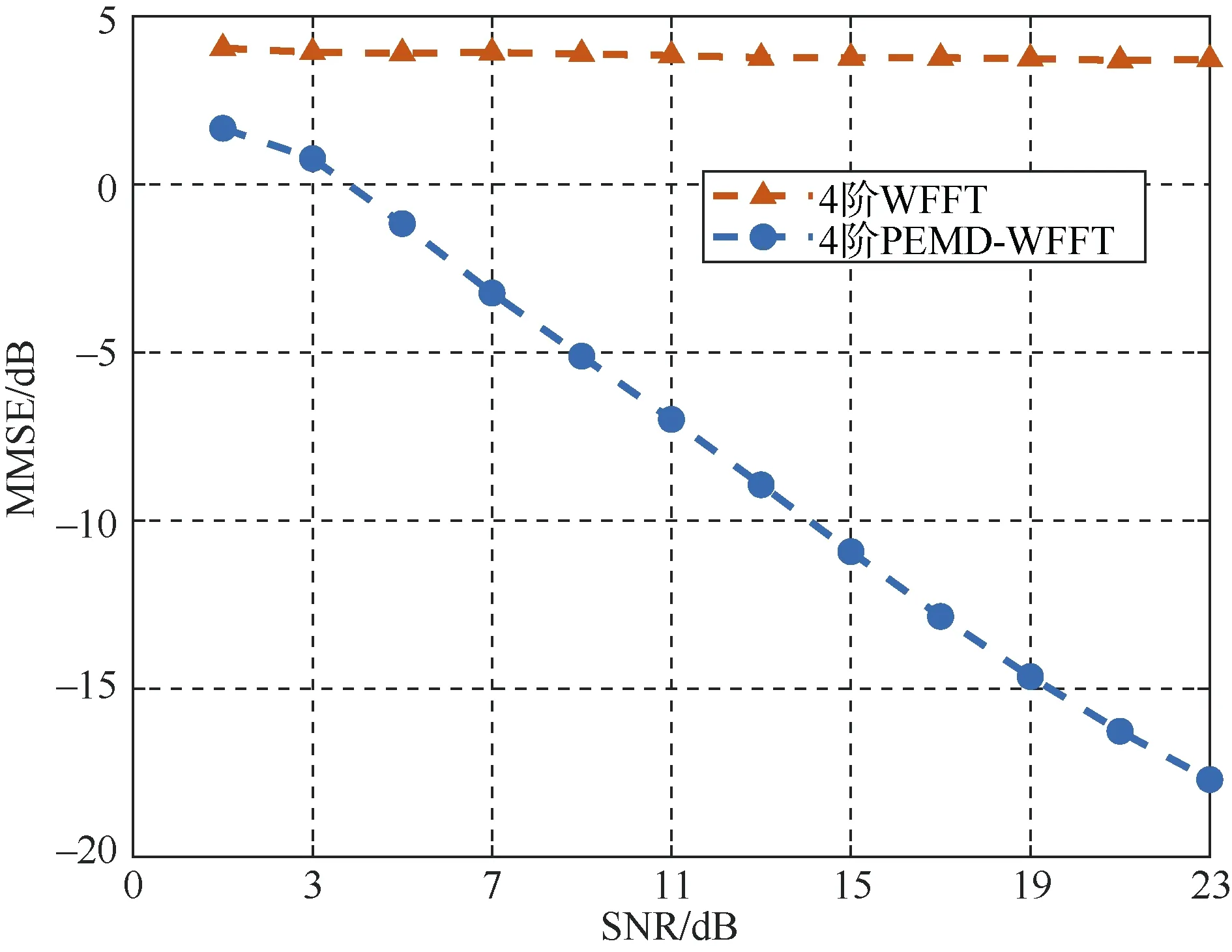
图7 相对速度7.32 m/s时信噪比变化仿真结果Fig. 7 Simulation results of the change of signal-to-noise ratio at a relative speed of 7.32 m/s
3 水池实验
为了验证算法性能,在水池进行了水声通信实验。发射换能器与接收水听器初始相距8 m,实验过程中水听器由人手持步行引入多普勒,人步行速度约为 0.6 m/s(因试验条件有限,仅采集了约0.6 m/s速度下的数据)。换能器为5~8 kHz换能器,水听器为标准水听器。子载波采用QPSK映射。
水池实验布放图如图 8所示,发送端与接收端初始相距 8 m,换能器与水听器分别置于水深3.5 m处。
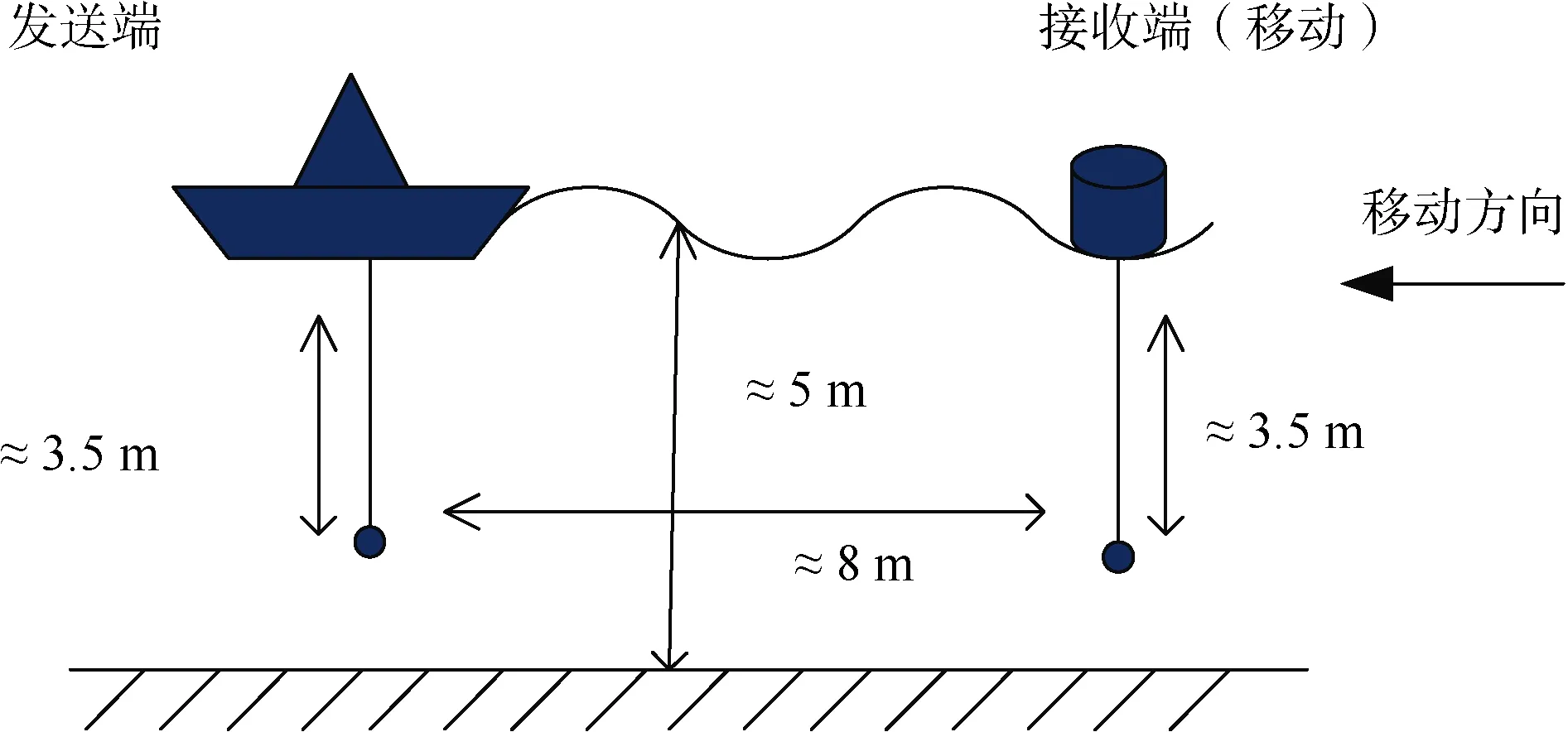
图8 实验布放图Fig. 8 Diagram of experimental deployment
图9为实际实验中的换能器位置。

图9 换能器位置Fig. 9 Location of transducer
实验中收发端的相对速度约为0.6 m/s。图10(a)为使用PEMD-WFFT算法解调星座图,图10(b)为WFFT解调后的信号星座图,由于接收端相对运动速度较小,产生的多普勒频移较小,2种算法的结果差距不大。

图10 水池数据解调结果Fig. 10 Demodulation results of pool data
4 结束语
本文对于多普勒补偿技术进行改进提出PEMD-WFFT多普勒补偿算法,仿真分析显示,在本文的仿真条件下,PEMD-WFFT算法可以对相对均匀运动速度不超过36 m/s的情况下引起的多普勒进行补偿。
尽管对现阶段的研究内容取得了一定成果,但鉴于时间有限和专业知识积累不足,本文研究的水声 OFDM多普勒补偿技术还需要进行更深一步的研究,如:
1)当收发端不再相对匀速运动,而是存在加速运动时,应进一步研究如何补偿加速度所带来的多普勒影响。
2)当OFDM系统载波个数增加,多普勒带来的影响更严重时,又该如何补偿。
