基于SWMM的不同坡度路侧生物滞留带水文性能分析
2021-07-13郑骁奇邵知宇龚华凤
郑骁奇,邵知宇,龚华凤
(1.林同棪国际工程咨询(中国)有限公司,重庆市401121;2.重庆市山地城市可持续交通工程技术研究中心,重庆市401121;3.重庆大学环境与生态学院,重庆市400045;4.重庆大学三峡库区生态环境教育部重点实验室,重庆市400045)
0 引言
海绵城市作为生态文明建设的重要组成部分,正逐步从规划阶段走向实施阶段。在这一过程中,政府对海绵城市建设的投入和支持力度逐年加大。2013年,习近平总书记提出“建立自然积存、自然渗透、自然净化的海绵城市”,首次提出了“海绵城市”的概念;2016年中共中央、国务院发布的《关于进一步加强城市建设管理工作的若干意见》明确提出应重点推进海绵城市建设,住房城乡建设部印发了《海绵城市专项规划编制暂行规定》,标志着海绵城市迈出了从概念到规划到实施的第一步;2016年至今,随着多个海绵城市项目在全国相继建成实施,海绵城市的重点也逐步从规划阶段进入实施阶段。
在实施阶段,路侧生物滞留带、雨水花园、透水铺装以及生态树池是市政工程中应用最广泛的海绵城市措施。掌握海绵城市措施的使用效果,明确影响使用效果的因素是成功建立自然积存、自然渗透、自然净化的海绵城市的先决条件。
路侧生物滞留带作为兼具路侧景观绿化、雨水净化以及下渗缓排功能的低影响开发措施,被广泛应用于国内外市政道路海绵城市建设中。国内对市政道路路侧生物滞留带的研究,侧重于水文特性影响因素的研究,主要集中在雨型条件、土壤特性、结构层厚度以及组合形式[1-15];对路侧生物滞留带坡度这一因素的研究较少,因而知之甚少。
同时,在日常的路侧生物滞留带设计过程中,“容积法”是目前计算路侧生物滞留带调蓄容积常用的一种方法,存在明显的局限性。由于我国海绵城市起步较晚,水文模型的普及率较低,为顺利推进海绵城市相关设计工作,在国家及地方相关设计导则中,提出了“容积法”这一简化方法,用于确定所需的海绵城市设施规模(面积、容积等)。“容积法”虽然简便、直观,但由于未考虑雨型、集流时间、地形坡度,生物滞留带坡度等因素,仅仅能计算总径流量,无法模拟峰值流量、外排流量等对海绵城市实施效果影响较大的指标。
因此,为研究路侧生物滞留带坡度对其使用效果的影响,探究滞留带纵向坡度的敏感性,同时比较简化后的日常路侧生物滞留带设计方法“容积法”与模型计算的差异,本研究将利用SWMM模型,对不同道路坡度下的路侧生物滞留带水文性能进行分析。研究主要分为以下四个部分:
(1)搭建正交分析模型:搭建不同比例不透水下垫面下的多个坡度道路的水文模型,模拟针对某一固定雨型和降雨量的生物滞留带蓄水调蓄效果,并通过试算法确定最小的所需海绵城市设施面积;
(2)通过“容积法”,计算不同比例不透水下垫面所需的最少海绵城市设施面积;
(3)对比模型和“容积法”得出的海绵城市设施面积;
(4)分析两种计算方法设施面积差异的原因,对改进“容积法”提出合理化建议。
1 模型搭建
1.1 基本参数
本研究通过SWMM搭建道路范围内的水文模型,模拟了4种不透水比例以及不同坡度正交组合的80个子汇水区的产流汇流的过程。80个子汇水区除坡度及不透水比例不同外,其他参数均相同。模型主要参数见表1,设计降雨序列见图1。

表1 模型参数表

图1 设计降雨序列图
1.2 正交组合模型
为探求道路坡度以及不透水比例对产流汇流过程的影响,本研究以坡度以及不透水比例为研究参数,模拟80个正交试验。
在不透水比例参数中,设置了4种不透水比例:60%、70%、80%以及90%;每一种不透水比例均设置了20种不同坡度,分别为:0.5%、1.0%、1.5%……9.5%以及10.0%。
在模拟完上述模型后,添加路侧生物滞留带海绵措施,针对每一种不透水比例,合理设置最小设施面积,使其在0.5%坡度的条件下不产生外排流量,并将该面积应用于剩余坡度的子汇水区中,计算模拟在不同坡度下,添加海绵城市措施后的径流及产流过程。
2 模型结果
2.1 不考虑海绵城市设施的模型结果
当未设置海绵城市措施时,在设计降雨序列下,每一种不透水面积模型均产生外排径流量。本研究总结整理了外排径流量时程变化,最大流量以及外排总量与坡度以及不透水比例的关系曲线。
就外流径流量时程变化而言,不同坡度在相同不透水比例条件下,外排径流量时程变化不大,因此仅列举0.5%、5%以及10%坡度条件下的外排径流时程变化见图2~图6。

图2 60%不透水比例外排径流量时程变化

图3 70%不透水比例外排径流量时程变化

图4 80%不透水比例外排径流量时程变化

图6 各个透水比例外排流量时程图
2.2 不同坡度、不透水比例的最大流量关系
针对最大流量与坡度及不透水比例的关系曲线而言,列举了从0.5%以0.5%坡度作为递增直至10%的20种坡度情况下的关系曲线,见图7~图11。

图7 60%不透水比例最大流量图

图8 70%不透水比例最大流量图

图9 80%不透水比例最大流量图

图11 不同不透水比例、坡度最大流量图
2.3 不同坡度、不透水比例的外排总流量关系
针对外排总量与坡度及不透水比例的关系曲线,列举了从0.5%以0.5%坡度作为递增直至10%的20种坡度情况下的关系曲线,见图12~图15。

图12 60%不透水比例最大流量图

图13 70%不透水比例最大流量图

图14 80%不透水比例最大流量图
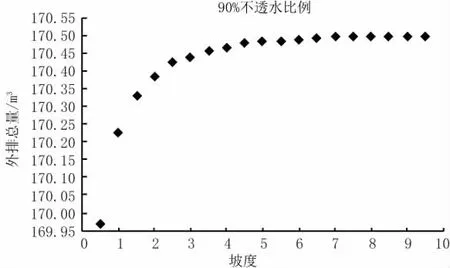
图15 90%不透水比例最大流量图
2.2 考虑海绵城市措施的模型结果
根据海绵城市设计要求,应设置海绵城市措施,使研究区域在设计降雨的条件下,不产生任何外排。针对不同的不透水比例,本研究通过试算法确定了在0.5%坡度情况下的最小的不产生外排的海绵城市设施面积。在确定了0.5%坡度情况下不产生外排的最小的海绵城市设施面积情况下,即在布置海绵城市设施后,研究区域最大径流量以及径流总量均为0。将此面积应用于1.0%~10.0%坡度的其他模型,以验证坡度是否对不产生外排的最小的海绵城市设施面积有影响,见表2。

表2 海绵城市设施面积
3 “容积法”计算方法
根据《海绵城市建设技术指南——低影响开发雨水系统构建(试行)》要求,实际工程中,常常使用“容积法”确定某一条市政道路所需的海绵城市设施面积。主要过程如下:
第一步:确定年径流总量控制率目标,该目标应根据地块类型,结合所在区域上位规划确定,以重庆为例,工业用地控制率65%,交通设施用地70%。
第二步:根据前述所确定的年径流总量控制率确定对应的降雨量。同样,该降雨量应根据地块所在城市降雨特性所确定,以重庆为例,见图16。
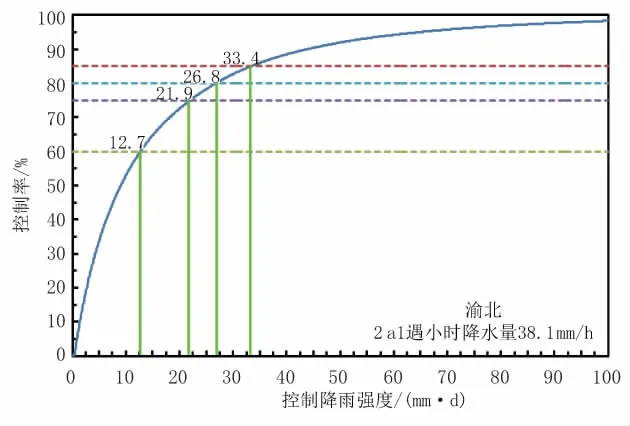
图16 年径流总量控制率与设计降雨量关系图
第三步:确定所需的调蓄容积。可根据以下公式确定:

式中:V为所需调蓄容积,m3;H为设计降雨量,mm,可根据第二步确定;φ为综合雨量径流系数,该雨量径流系数应根据地块不同下垫面及对应雨量径流系数根据面积加权确定;F为汇水面积,hm2。
第四步:合理布置海绵城市措施的位置及面积,就市政项目而言,由于用地较为紧张,应避免为了海绵城市而单独拟定用地,宜结合道路及绿化范围确定。充分利用绿化用地,结合景观综合打造。尽量靠近车行道,实现雨水源头控制的既定功能。
第五步:合理拟定路侧生物滞留带的结构形式参数,应尽量减少生物滞留带下凹深度,避免造成安全隐患。在确定结构形式后,应计算单位面积调蓄能力。
第六步:根据第四步确定的海绵设施面积、第五步海绵城市单位面积调蓄能力共同确定海绵城市措施能够提供的调蓄容积。
第七步:应对比第六步计算的海绵城市设施能够提供的调蓄容积及第三步所需的调蓄容积,确保海绵城市设施能够提供的调蓄容积大于所需的调蓄容积。当不满足时,应增大海绵设施面积或调整海绵城市结构参数提高单位面积调蓄雨水能力。
3.1 “容积法”计算参数选取
3.1.1 设计降雨
选取70%年净流总量控制率作为目标,对应设计雨量为18.9 mm。该设计雨量同图2设计降雨序列图降雨总量数值相同。
3.1.2 下垫面雨量径流系数
道路红线范围内,一般分为不透水路面、透水铺装以及绿化三种类型下垫面,为简化计算并使其下垫面面积分布同前文模型计算保持一致,在“容积法”计算中,将绿化面积全部作为海绵城市设施面积:即不透水路面面积、透水铺装面积、绿化面积(海绵城市设施面积)三者之和等于研究区域总面积。
此外,在不同类下垫面雨量径流系数选取方面,由于“容积法”计算中,考虑到了透水铺装下垫面仅承担降落到自身上的雨水,储存在透水铺装空隙中,并不产生外排,对整个研究区域径流无影响,因此径流系数取0,相反由于海绵城市设施不仅承担降落在自身上的雨水,还会承担由于不透水路面产生的雨水,因此径流系数取1。对于不透水路面而言,模型中未考虑其蓄水能力,因此全部产生径流,因此径流系数取1。
3.1.3 生物滞留带结构参数
为保证“容积法”和模型计算结果具有可比性,生物滞留带结构采取和模型中相同结构,设置见表3。

表3 生物滞留带结构参数
3.2 “容积法”计算结果
通过单变量求解,确定最小的海绵城市设施面积见表4、图17。

表4 海绵城市设施面积(“容积法”)

图17 不同不透水比例海绵城市设计面积比例图
4 结果分析与对比
4.1 模型结果分析
对同一不透水比例区域而言,其径流产流时程曲线随降雨强度变化而变化,趋势上保持高度一致,但整体时间上略有滞后,即降雨一段时间后产生径流,降雨结束后一段时间依然产生径流。在相同不透水比例下,不同坡度对其径流产流时程曲线的影响不明显,见图2~图5。相反,当坡度一定时,径流产流时程曲线同不透水比例呈正相关关系:即不透水比例越大,径流产流量越大,见图6。

图5 90%不透水比例外排径流量时程变化
对同一不透水比例区域而言,其最大径流量随着坡度呈正相关关系,但整体而言增加趋势并不明显。当研究区域坡度小于5%时,最大径流量随坡度的增加而增加;当研究区域坡度大于等于5%时,最大径流量几乎不随坡度变化,见图7~图10。因此,可以判断坡度对于最大径流量影响较小。相反当坡度一定时,最大径流量同不透水比例关系较大:不透水比例越大,径流产流量越大,见图11。
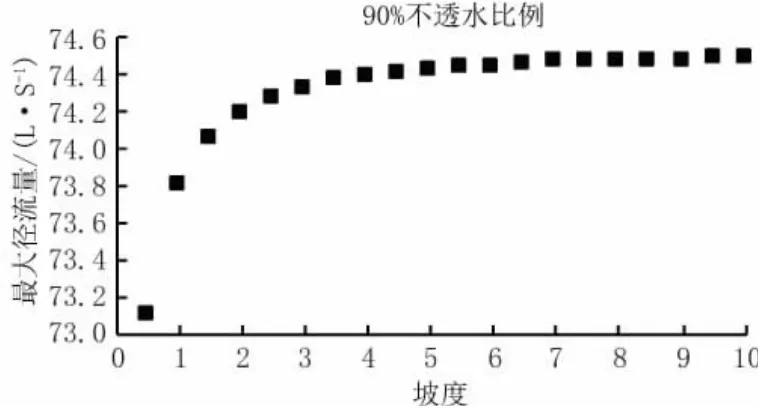
图10 90%不透水比例最大流量图
对同一不透水比例区域而言,其外排总径流量随着坡度的增加而先增加后减少,但整体而言增加趋势并不明显。当研究区域坡度小于5%时,外排总径流量随坡度的增加而增加;当研究区域坡度大于等于5%时,外排总径流量随坡度的增加而减少,见图12~图15。当坡度一定时,外排总径流量同不透水比例关系较大:不透水比例越大,外排总径流量越大。
对同一不透水比例区域而言,海绵城市措施面积大小同坡度无关系,按照0.5%坡度设计的海绵城市措施面积能够满足1.0%~10%的所有模型的海绵城市目标要求。相反当坡度一定时,不同不透水比例对海绵城市措施面积大小有明显影响,不透水比例越大,海绵城市措施面积越大,见表2。
根据正交模型结果分析可以看出,无论是从径流时程、最大径流量还是海绵城市设施面积、外排径流总量来讲,坡度对以上四者影响因素均较小;相反,不透水比例影响较大:不透水比例越大,最大径流量、外排径流总量、径流时程流量以及海绵城市设施面积均越大。根据上述分析可知,生物滞留带坡度对其水文影响较小,在进行生物滞留带设计时,应优先考虑设施面积、结构层性质以及设置位置等因素,坡度可作为次要因素进行考虑。相反,在进行生物滞留带设计时,应重点考虑不透水比例,根据不透水比例,确定所需调蓄容积,进而确定设施面积。
场地水文过程受不透水面积比例影响较大,受坡度影响较小。针对该模型结果,本文进行了如下分析并间接论证了模型的正确性。首先,SWMM模型采用考虑水量平衡及曼宁公式的非线性水库法。根据SWMM软件帮助手册可知,模型在进行地表水径流模拟的时候,采用的是非线性水库法,即通过水量平衡法以及曼宁公式试算确定地表径流:V进=V出+V储。
根据图18所示:进入场地的水(V进)有:降雨;上游场地来水。针对所有场地,降雨都相同,且所有场地均无上游场地来水,因此针对所有场地,进入场地的水量均相同。离开场地的水;离开场地的水(V出)有:下渗;地表径流。针对所有场地,下渗采用Horton模型且所有参数均相同,因此下渗水量相同。储存于场地的雨水(V储存)根据模型设计,不透水下垫面有一定的下凹深度ds,用于模拟不透水下垫面蓄水能力,因此,不透水比例一定的情况下,其下凹蓄水量相同。因此,根据水量平衡原理,在不透水比例一定的情况下,海绵城市设施面积、外排径流总量均基本相同。

图18 S WMM计算模型原理示意图
其次,在确定最大流量时,可通过国家规范进行简化计算,该简化计算仅考虑曼宁公式,并未考虑水量平衡。该方法能够验证坡度对设计峰值流量(即最大流量)影响较小。具体计算过程如下:根据《公路排水设计规范》(JTG/T D33—2012)9.1.4坡面汇流历时计算公式可知:坡面汇流在地表粗度系数、坡面流长度一定的情况下,仅和坡面坡度有关。计算公式如下:

式中:t为汇流时间,min;M为地表种类参数,沥青路面取0.13;L为汇流长度,m;i为道路坡度。
在计算汇流时间后,应根据重现期及汇流时间,计算各地区暴雨强度(重现期5 a)。公式如下:

式中:q为暴雨强度,单位为L/s;P为暴雨重现期,取5;T为汇流时间,单位为min。
根据上述公式,计算了该场地的暴雨强度与场地坡度之间的关系(以60%不透水率为例),见图19。

图19 暴雨强度与坡度关系图
根据图19可知,坡度对最大暴雨强度影响较小,因此对最大径流量影响也较小。其内在原因在于坡度仅影响地表径流汇流时间,且该时间对暴雨强度影响较小。
综上所述,可以得出以下结论:(1)通过国家规范进行简化计算的结果同模型法计算趋势是一致的,能够进一步证明坡度对水文过程影响较小;(2)基于SWMM的模型法同基于国家规范的简化计算相比,在考虑曼宁公式的基础上,进一步考虑了水量平衡,结果更准确。
4.2 “容积法”结果分析
根据“容积法”计算过程可知,在计算研究区域所需调蓄容积时,无法计算径流时程变化、无法计算最大外排流量。在计算生物滞留带调蓄容积时,未考虑生物滞留带表层植物对蓄水体积的占用,在计算土壤层蓄水时,将整个土壤空隙均纳入蓄水计算范围,与实际下渗过程存在误差。因此综上所述,“容积法”计算结果和实际情况具有一定的系统误差。根据“容积法”计算结果可知,海绵城市设施规模随着不透水比例增加线性增加:即不透水比例增加10%,设施规模增加0.62%,见图16。
4.3 模型结果与“容积法”计算结果对比
根据模型结果与容积法结果,针对不同不透水比例,见表5。

表5 模型法、容积法面积对比
根据以上结果可知,“容积法”和模型计算结果有较大出入,针对同一不透水比例,模型法计算结果均为“容积法”计算结果的1.4倍左右,不随不透水比例变化而变化,具有较强的一致性。由此可见,“容积法”在确定海绵城市设施规模时,计算结果偏小,偏“不安全”。如按照该容积进行设计和建造,在设计雨量的情况下,会导致研究区域产生外排,不满足海绵城市设计要求。
4.4 改进的“容积法”
根据4.3模型结果与“容积法”计算结果对比可知,“容积法”计算结果同模型结果相比偏小,调蓄容积不足,导致研究区域产生外排,不满足海绵城市设计要求。因此有必要对“容积法”进行改进。
通过“容积法”确定海绵城市设施规模的过程中,其误差主要来自于单位面积海绵设施调蓄能力计算。在通过“容积法”计算单位面积海绵城市调蓄能力过程中,进行了若干假设:生物滞留带蓄水层深度为设计下凹深度,未考虑种植灌木、乔木等植物对生物滞留带蓄水层深度的影响。实际工程中,由于植物影响,会导致生物滞留带有效蓄水深度小于设计下凹深度;渗透系数为常量,不随土壤含水率变化,根据《海绵城市建设技术指南——低影响开发雨水系统构建(试行)》,计算调蓄容积可考虑两小时土壤下渗水量,渗透系数为常量。实际工程中,渗透系数随初期土壤含水率、饱和含水率以及下渗时间影响,是一个变量,相反,SWMM模型在计算该部分下渗量时,采用的是改进的霍顿模型,比“容积法”中直接采用常量更加准确;土壤有效孔隙率,在“容积法”中,土壤孔隙率用于计算土壤空隙蓄水量,由于土壤厚度较大,孔隙率的合理选择对土壤空隙需水量有较大影响,并且该参数在实际工程中,具有很大的不确定性。因此,建议在进行“容积法”计算中,不考虑土壤蓄水,偏于保守的计算海绵城市设施单位面积蓄水能力。改进后的“容积法”在计算海绵城市设施单位面积蓄水过程中,采用了如下假设:设计下凹深度考虑20%折减作为有效下凹深度;透系数根据SWMM模型计算结果计算两小时平均渗透系数;不考虑土壤空隙蓄水。基于此,计算了海绵城市设施面积。改进后的“容积法”结果与模型结果,汇总见表6。

表6 模型法、改进容积法面积对比
从两者结果的对比上来看,改进后的容积法,能够较好的计算出所需的海绵城市设施面积。能够解决一般容积法计算结果偏小这一不足,具有一定的工程应用价值和意义。
5 结论及建议
本研究通过搭建考虑海绵城市措施的道路水文水动力模型,模拟了四种不透水比例下的二十种不同纵坡的道路径流产流过程,分析了坡度和不透水比例对径流过程、最大径流量、外排总径流量的影响;在此基础上,通过试算法确定了针对每种不透水比例下的海绵城市设施面积。此外,根据模型的相关参数,通过“容积法”确定了每种不透水比例下的海绵城市设施面积。最后,比较和分析了考虑海绵城市设施的模型法和容积法计算结果的差异及原因,对“容积法”进行了改进。通过本研究,得出了以下结论:(1)针对同一降雨序列,坡度越大,最大径流量、径流过程流量以及总的外排流量越大,但影响不显著;(2)针对同一降雨序列,不透水面积比例越大,最大径流量、径流过程流量以及总的外排流量越大,且影响显著;(3)海绵城市设施面积不受坡度影响,但受不透水面积比例影响,且线性相关;(4)针对四种不透水比例下的海绵城市设施面积计算,“容积法”均偏小,应进行修正,修正后的“容积法”能够更加准确的计算海绵城市设施规模。
在海绵城市设计中,除年径流总量控制率这一指标外,还有污染物去除率指标。因此,未来的研究可以通过模型探求坡度、生物滞留带结构形式以及类型对不同污染物去除率的影响。并且可以将模型结果同“容积法”计算结果进行比较和分析,对“容积法”计算污染物去除率的结果进行优化
