主从遥操作手术机器人的主手附加位移补偿

2021-07-13贠今天李浩然

天津工业大学学报 2021年3期

贠今天，李浩然

（1.天津工业大学机械工程学院，天津 300387；2.天津工业大学天津市现代机电装备技术重点实验室，天津300387）

遥操作机器人技术是现今机器人技术发展的前沿，在未来的医疗领域极具应用价值[1-3]。遥操作手术机器人技术解决了医生与患者远距离手术的问题，使患者能够在最佳时间得到救治，节省了时间和人力成本。

遥操作手术机器人技术中准确的力反馈与精确的位置控制，即遥操作中良好的透明性[4]，一直是遥操作所追寻的目标。准确的力反馈能够使医生在手术过程中更加具有沉浸感[5]，使医生能够更真实地感受手术器械与患者身体组织之间的相互作用力[6-7]；精确的位置控制[8-9]使得医生操作手术刀切割患者身体组织更为理想和安全。目前，在实际的遥操作运行过程中还存在定位精度和误差的问题[10]。凌颢等[11]选用拉格朗日方程建模，并依据模型特征在模型中补入Stribeck摩擦模型，对机器人主操作手的杆件重力、惯性力以及摩擦力进行补偿，提高了主操作手的精确性。Meli等[12]运用皮肤反馈代替触觉反馈“感觉减法”，超越了其他非运动性的遥控操作中的反馈技术，使遥操作力反馈更为准确。Park 等[13]发现如果环境刚度小于基于无源能量边界法稳定的可显示刚度，就可以通过设置能量边界法中的第2 个控制参数来提高遥操作系统的透明性。桑宏强等[14]针对现有微创外科手术机器人缺乏力感知和力反馈问题，提出了基于外力观测器的微创机器人鲁棒滑模双边力反馈控制结构，提高了微创手术的操作精度。Li 等[15]在假设电机编码器读数和电机输出转矩已知的情况下使用无传感器卡尔曼滤波器估算操作者握力、从动马达和夹爪位置和速度，提高反馈系统的透明性。宋莹莹等[16]采用BP 神经网络对力反馈模型误差进行补偿。

为减小遥操作中主操作手附加位移对手术精度的影响，本文针对遥操作过程中人体手臂反应延迟和由于采用力反馈-位置型控制结构导致的力-位耦合而产生附加位移的问题，采用质量-弹簧-阻尼模型来模拟遥操作过程中人体手臂的反应、主操作手的响应以及它们之间的交互关系，建立了附加位移补偿模型，通过仿真与实验验证该补偿方法的施行效果。

1 主操作手动力学模型建立

1.1 主操作手动力学基础模型

本文只考虑主操作手的位置信息，故建立三自由度动力学模型。主操作手PHANToM Desktop 的结构简图如图1 所示。

图1 主操作手结构简图Fig.1 Structural sketch of master manipulator

主操作手的基础模型可以表示为：

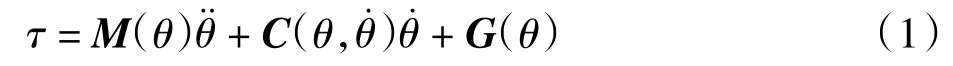
式中：τ∈R3为关节力矩，即控制输入为主操作手的关节位置、速度、加速度；M（θ）∈R3×3为正定惯性矩阵为哥氏力及离心力矩阵；G（θ）∈R3为重力矢量。

1.2 含关节摩擦力的主操作手动力学模型

为了使操作者感受更真实的反馈力信息，考虑在主操作手的基础模型中加入摩擦力模型。摩擦力模型本身具有复杂性与不确定性，同时选定的摩擦力模型也要便于线性化处理，Coulomb+Viscous 组合摩擦模型为该研究摩擦力模型的最佳选择。

Coulomb+Viscous 摩擦模型可表示为：

式中：Fc为 Coulomb 摩擦因数；Fv为 Viscous 摩擦因数；为接触过程中接触面的相对速度。本次研究中的主操作手具有3 个关节，故整体的摩擦模型可以表示为：

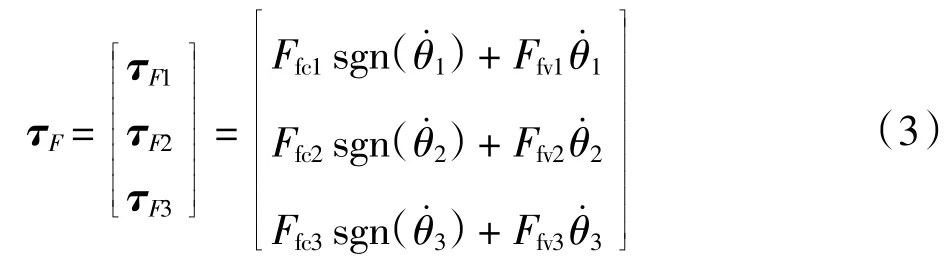
得到的主操作手完整动力学模型为：

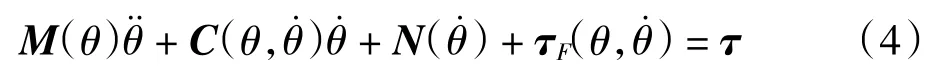
将得到的完整动力学模型进行线性化处理：

式中：Y 为 3 × 18 维回归矩阵；ψ为 18 × 1 维动力学参数向量。依据文献[17]确定相关动力学参数。

2 主操作手附加位移补偿策略

2.1 主操作手附加位移产生原因

为了更好地实现主从控制和力反馈，主从遥操作手术机器人系统采用力反馈-位置型主从控制结构。但实际运行过程中，反馈过程会受到力信息和位置信息相互耦合的影响而产生附加位移。另一方面，人体对于外界环境的反应存在延迟效果，延迟时间大概在100~300 ms，在这期间主操作手自由运动产生附加位移。人体接到反馈力信息后，至少在100 ms 后，神经网络系统开始反应，主操作手的附加位移被抑制。主操作手附加反馈如图2 所示。

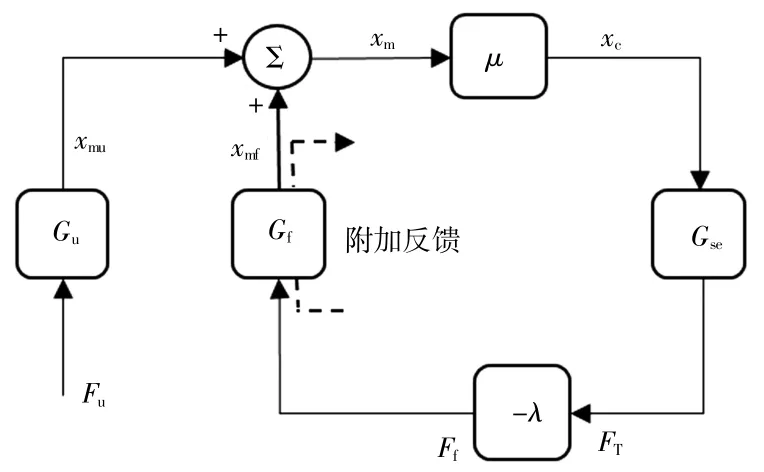
图2 主操作手附加反馈Fig.2 Additional feedback from master manipulator

图2 中，Gu为操作者输出力转化为期望位移的传递函数；Gf为从端力转化主端位移的反馈函数；Gse为从端环境与从操作手力与位移转化的传递函数。

2.2 主操作手附加位移补偿策略

本文在原有控制结构的基础上加入能够计算附加位移量的附加位移模型，进而形成附加位移补偿策略，如图3 所示。在反馈过程中，将从端反馈力通过附加位移模型获得附加位移将附加位移与主操作手的实际位移叠加作为指令传递给从端。补偿策略中表示主操作手位移的预测模型表示附加位移模型估计的附加位移量表示操作者施加力后的期望位移。

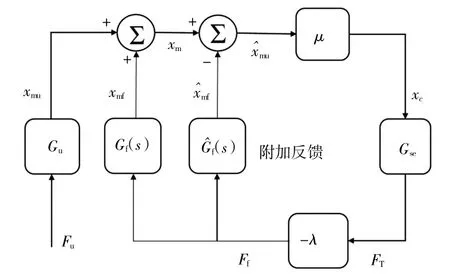
图3 主操作手附加位移补偿策略Fig.3 Additional displacement compensation strategy of master manipulator

根据上述主操作手附加位移补偿策略，得到该主手附加位移补偿策略的系统传递函数为：

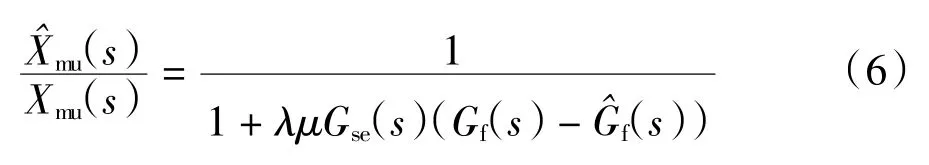
在研究过程中发现，在人手带动主操作手运动的过程中，主操作手内部的响应、主操作手与人手之间的交互（如图4 所示）以及人体反应延迟的过程，可以运用如图5 所示的质量-弹簧-阻尼模型来模拟。图5中：Fm为主操作手关节电机的输出力；Fh为主操作手末端所受到的力；FH为操作者手部所受的力；mm为主操作手关节电机的等效质量；mh为主操作手杆件的等效质量；Mh为在操作者抓持主操作手运动过程中人手的等效质量；b1、b2为操作者的手操作主手的等效阻尼；km、bm为主操作手的等效刚度与阻尼；k1、k2为操作者的手操作主手的等效刚度；xm为主手编码器所测量的关节电机的运动位移；xh为力反馈主手末端点的运动位移；xH为操作者手的运动位移。

图4 人手与主操作手的实际交互Fig.4 Actual interaction between human hand and master manipulator

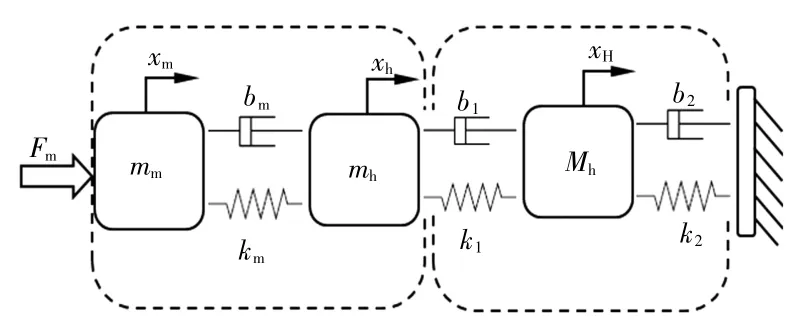
图5 人手-主操作手的质量-弹簧-阻尼模型Fig.5 Mass-spring-damping model of human hand-master manipulator

为了便于研究，本文将图5 所示质量-弹簧-阻尼模型分解为图6 所示的主操作手模型和图7 所示的人手模型。

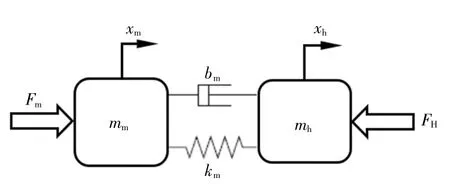
图6 主操作手模型Fig.6 Master manipulator model

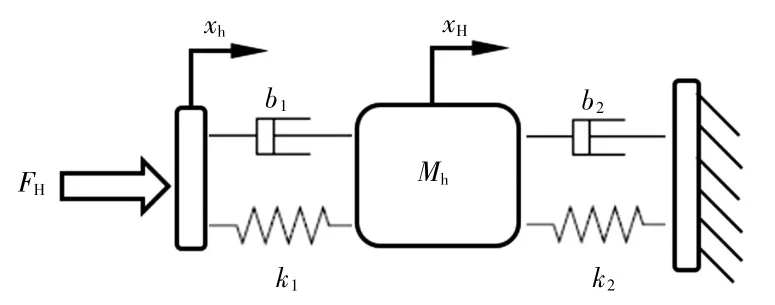
图7 人手模型Fig.7 Human hand model

经过计算得到人手的传递函数模型Gh和主操作手的传递函数模型Gm：

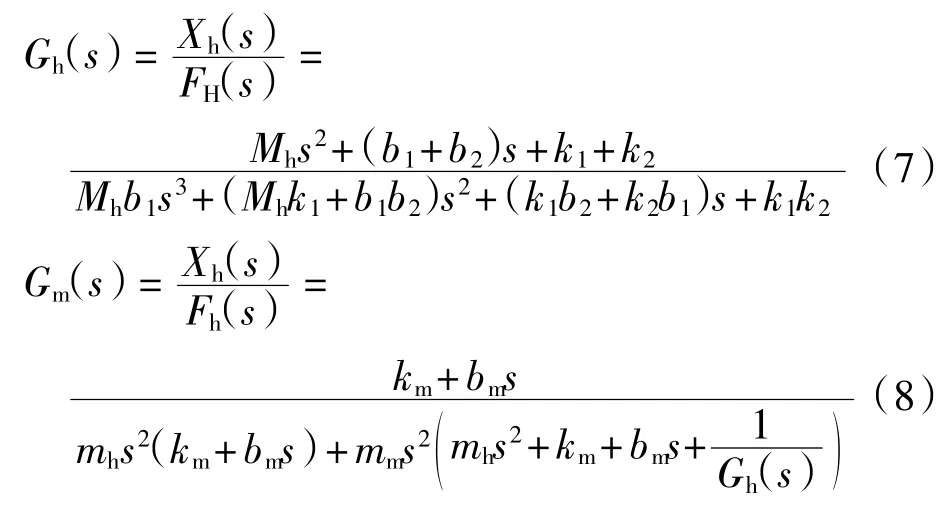
人手与主操作手的交互关系模型如图8 所示。

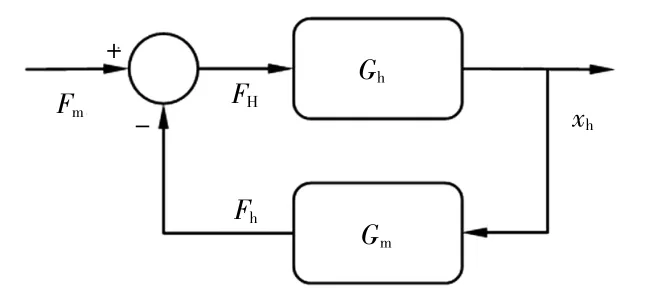
图8 人手与主操作手的交互关系Fig.8 Interaction between human hand and master manipulator

根据图8 可得到人手与主操作手构成的闭环传递函数模型：

参考文献[18]通过实验所辨识的主操作手相关参数，如表1 所示。另外考虑人手的反应时间，确定质量-弹簧-阻尼模型的相关参数为：km=39 500 N/m，bm=3.6 N·s/m，mh=0.471 6 kg，mm=0.010 75 kg，b2=7 N·s/m，k2=330 N/m。

表1 人手-主操作手模型相关参数Tab.1 Related parameters of human hand-master manipulator model

对本文建立的人体手臂模型的响应部分给予1 N的激励，模拟手臂从接到力反馈信息开始到达到稳定阶段的响应情况，结果如图9 所示。

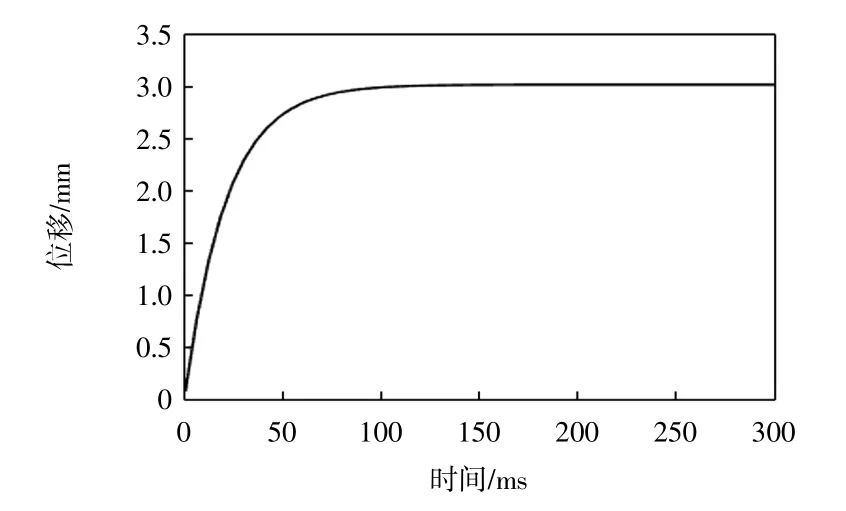
图9 人手模型响应曲线Fig.9 Response curve of human hand model

由图9 可以看出，从手臂响应开始到响应稳定时间大约为100 ms，符合手臂响应的实际情况（100~300 ms），说明该模型可用。

3 主操作手附加位移补偿策略仿真与实验

3.1 主操作手附加位移仿真

为了更为直观地反映受主操作手内部响应以及人体反应延迟的影响而产生的附加位移，本文假设实际手术过程中，医生手臂的反应时间为100 ms。在反馈力为1 N 的情况下，100 ms 内主操作手末端在X、Y、Z 3 个方向上的位置变化如图10 所示。

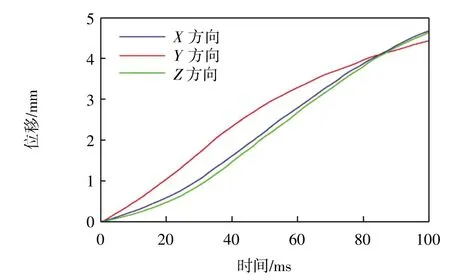
图10 主操作手末端位置在X、Y、Z 3 方向的附加位移Fig.10 Additional displacement of end position of master manipulator in X，Y，and Z directions

由图10 可以看到，主操作手因为自身特性以及操作者反应延迟，在X、Y、Z 3 个方向产生了不可忽略的附加位移，故对附加位移的补偿研究是十分必要的。

3.2 主操作手附加位移补偿实验研究

实验室现有的实验平台如图11 所示，包括主操作手PHANToM Desktop、从操作手WAM Arm 从手以及PC 机一台。其中，主操作手能够记录操作过程中主手的关节位置、速度及力矩，从操作手编码器能够记录从操作手关节位置，其末端的触感球根部的传感器能够采集从操作手末端的三位轴向力和力矩。

图11 主从遥操作力反馈实验平台Fig.11 Experiment platform for force feedback of master-slave teleoperation

本次实验共进行2 次：

（1）在第1 次实验中，在没有附加位移补偿的原始控制系统下，人手带动主操作手从标定点A 运动到标定点B，如图12 所示，从而控制从操作手末端的触感球推动在指定位置放置好的纸箱。从操作手编码器所记录的从操作手运动为补偿前位移。

图12 实验中的标定点Fig.12 Calibration points in experiments

（2）第2 次实验中，在含有附加位移补偿的控制系统下，同样使主操作手由标定点A 运动到标定点B，带动从操作手推动在同样位置放置的纸箱，此次从操作手编码器记录的从操作手运动为补偿后位移。主操作手运动通过模型理论计算映射到从操作端的运动为期望位移。

将实验数据导入MATLAB 中进行处理，得到X、Y、Z 3 个方向上的补偿前位移、期望位移与补偿后位移对比图，如图13 所示，图13 中红色虚线代表补偿前位移，黑色点划线代表期望位移，蓝色实线代表补偿后位移。

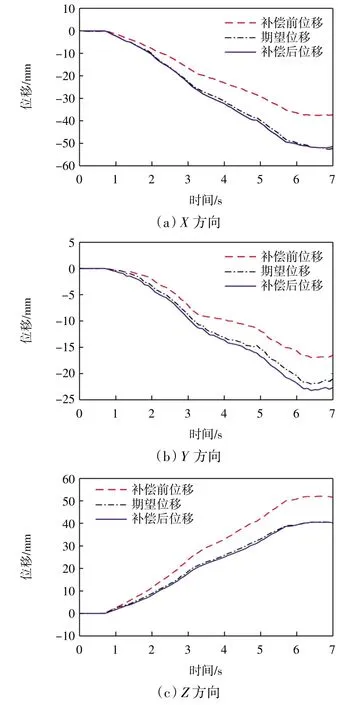
图13 X、Y、Z 方向补偿前位移、期望位移与补偿后位移对比Fig.13 Comparison of pre-compensation displacement，expected displacement and compensated displacement in X,Y and Z directions

由图13 可以发现：主操作手带动从操作手运动的过程中，由于操作者反应时间和主从控制结构的影响而产生了不可忽略的误差。图13 中，补偿前位移（红色虚线）在一定程度上偏离了期望位移（黑色点划线），而经过补偿后的位移（蓝色实线）与期望位移（黑色点划线）拟合程度非常高。从操作手运动在补偿前后的均方根误差如表2 所示。

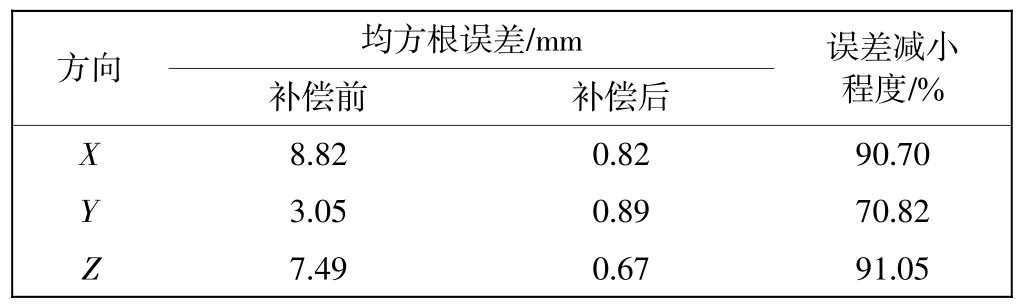
表2 主操作手附加位移补偿前后的均方根误差对比Tab.2 Comparison of root mean square error before and after additional displacement compensation of master manipulator

由表2 可知, 该控制策略将主从遥操作在X、Y、Z 3 个方向上的运动控制精度分别提高了90.70%、70.82%和91.05%，进而说明所提出的主操作手附加位移补偿策略是有效的，通过采用质量-弹簧-阻尼模型模拟人体手臂的反应特性、人手与主操作手的交互特性以及主操作手本身特性所建立的附加位移补偿模型是正确的。