一类非线性分数阶微分方程的数值解

金艳玲

(山西大学商务学院，数学教研部，太原 030031)

分数阶微积分是一个古老的课题，分数阶微分方程在高能物理、化学、医学、生物学等方面都有着广泛的应用。探讨微分方程的求解方法尤为重要，但精确解却很难获得。很多学者在分数阶微分方程的数值解方面都做了大量的研究。文献[1]采用了基本的分数差分法、Adomain分解法、和变分迭代法对一类线性分数阶微分方程的数值解进行了讨论，并利用实例给出各种方法计算效果的对比。文献[2]利用样条插值方法讨论了一类非线性微分方程的数值解。[3]则用分数样条法解决了分数阶线性微分方程组的数值解。文献[4]-[9]讨论了小波分析方法在分数阶微分方程求解中的应用。则在文献[1]所讨论的方程中，改变其分数阶导数项，并利用分数差分法探讨其解。

1 基本概念

在分数阶微积分的发展过程中，出现过以下几种基本定义Riemann-Liouville分数阶积分算子：

(1)

J0f(x)=f(x)，

(2)

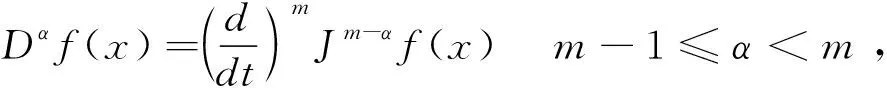
(3)

Caputo意义下函数f(x)的分数阶导数

(4)

注：DαJαf(x)=f(x)

(5)

Gr-nwald-Letnikov意义下的分数阶导数

(6)

2 主要方程

主要讨论了如下方程：

(7)

文献[1]中讨论的方程为下列方程中g(t)=1的情况。

特别地，当g(t)=1,n=1,0<α≤1时，此方程的形式恰为分数阶弛豫方程：

(8)

当g(t)=1,n=2,1<α≤2时，此方程的形式恰为分数阶振荡方程：

(9)

3 方法讨论

差分法是解决微分方程数值解的有力工具。对于分数阶微分方程，利用Grnwald-Letnikov意义下的分数阶微分的定义及其等价性，使用分数差分法也是行之有效的。所以，对于上述微分方程，我们利用定义3可以得到以下差分形式：

(10)

其中：tn=nhun=u(tn)

(11)

(12)

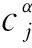
4 数值算例

我们考虑如下方程

(13)

其中

(14)

经过探讨可知，该方程的精确解为u(t)=t3-t2

利用分数差分法，使用递推公式

(15)

利用Matlab软件，分别取步长为0.1和0.01，可得到数值解与真值对比图如下:

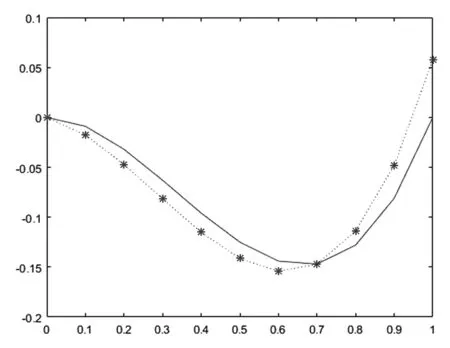
通过上述例子的讨论，并由图表可以看出，数值解与精确解的对比数据，误差随着h的减小而减小，进一步说明该算法在求解此类分数阶微分方程中很有效。