考虑脉动风下弓网离线影响的高速铁路接触网可靠性分析*

朱鹏宇，万后林，张 鹏

(1.淮阴工学院 建筑工程学院，江苏 淮安 223000；2.江苏东辰建材有限公司，江苏 淮安 223000)

0 引言

高速铁路牵引供电系统中，因接触网设备长期户外运行，易受自然环境影响。至2020年底，我国铁路运行里程达14.6万km，其中高铁约占20%[1]。列车高速运行对弓网间良好受流要求较高，弓网间良好受流决定供电质量好坏及行车可靠性[2]。国内外学者针对接触网抗风稳定性做大量研究，但仅停留在通过建立受电弓、接触网模型研究两者间相互作用，关于风与弓网2者干扰问题研究较少[3-5]。文献[6]表明接触网系统受脉动风影响形成抖振，增加弓网间离线率。弓网离线使受流不连续影响列车平稳运行，离线电弧产生高温，降低接触线使用寿命以及供电稳定裕量。目前，针对接触网结构研究，忽略自然环境尤其是西北地区脉动风对接触网系统可靠性影响。

因此，本文通过谐波叠加法模拟西北地区脉动风风速时程，对风速区间分布概率进行统计，将脉动风下弓网接触压力及弓网离线率作为衡量接触网系统可靠性新指标，利用接触网系统GO-FLOW模型对脉动风下接触网可靠性进行分析。

1 脉动风场模拟

自然风具有随机性与不确定性，在顺向时程曲线中，将自然风分为平均风和脉动风：平均风频率低，对接触线产生作用力为静力[7]；脉动风强度随机更替，周期短，对接触线作用力引起弓网振动。因此，本文主要集中于脉动风研究。

在三维空间内，某处自然风速如式(1)所示：

(1)

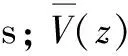
时域法需通过现场实测、风洞试验等获取风速时程样本，过程比较繁琐。因此，本文采用数值模拟法模拟风速时程。

1.1 脉动风场数值模拟方法

常用脉动风速时程仿真手段包括[8]线性自回归滤波(AR)法、谐波积累(WAWS)法、随机傅里叶特征法及小波重构法。其中，WAWS法具有适用范围广、模拟精度高等优点，适用于接触网脉动风场模拟。脉动风概率符合高斯分布，将脉动风变换为一维零均值平稳高斯随机过程向量，如式(2)所示：

v(t)={v1(t),v2(t),…,vM(t)}T

(2)

则互谱分布函数矩阵如式(3)所示：

(3)

对式(3)进行Cholesky分解，结果如式(4)～(5)所示：

S(ω)=G(ω)·G*T(ω)

(4)

(5)

空间中任意点x时程曲线如式(6)所示：

(6)

式中：Δω=ωup/N为频率增量；ωup=ωmax-ωmin为截止频率；i=1,2,3,…,n；N为数值足够大的正整数；Gim为G(ω)中元素；θim为|Gim(ωml)|幅角，(°)；ωml为双索引频率。

1.2 脉动风速功率谱函数选取

本文将Davenport谱作为脉动风速功率谱函数[8]，如式(7)所示：

(7)

式中：f为脉动风频率；S(f)为Davenport谱函数；k为风区所在地的地面粗糙度系数；v10为标准高度为10 m某点平均风速，m/s。

在空间中，任意两点间互功率谱如式(8)所示：

(8)

式中：Saa(ω)、Sbb(ω)分别表示a、b自功率谱函数；coh(Δab,ω)为a、b相关性函数；ω为角频率；Cx表示空间任意两点相关性在x方向衰减程度系数；U(z)为导高处平均风速，m/s；φ(ω)为风速相位角。其中，φ(ω)如式(9)所示：

(9)

式中：Δx=|xa-xb|表示a、b在x方向距离。

将风区参数数据代入式(7)～(9)得到自功率谱及该风区互功率谱系数，构成互功率谱函数矩阵；对互功率谱函数作Cholesky分解，将结果汇总代入式(6)，通过MATLAB仿真模拟得到风速时程曲线。

2 接触网脉动风场仿真

2.1 接触网脉动风风速时程仿真

基于MATLAB平台，采用脉动风速功率谱函数对西北某风区单点脉动风速进行仿真[9-10]。WAWS法模拟脉动风仿真参数见表1。

表1 WAWS法模拟脉动风仿真参数

脉动风风速时程曲线如图1所示。由图1可知，脉动风分布于-30～30 m/s，正负号代表脉动风风向。

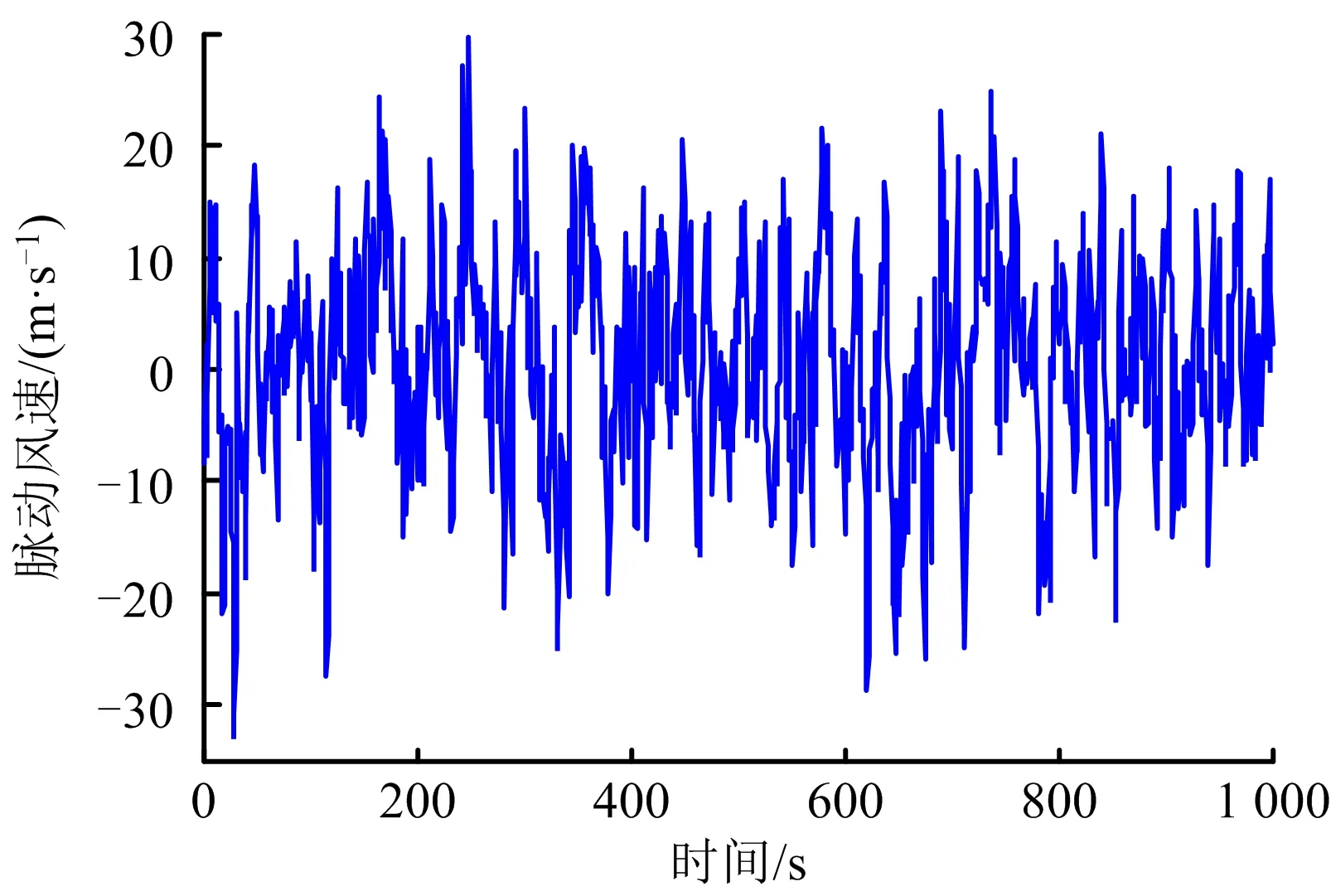
图1 脉动风风速时程曲线

2.2 脉动风风速概率分布

脉动风风速时程曲线符合高斯分布，由图1可知，高斯分布参数μ=0.563 9，σ2=9.603。利用MATLAB绘制脉动风速概率分布如图2所示。

图2 脉动风风速概率分布

利用Normspec函数计算得到脉动风风速概率，脉动风风速概率分布统计见表2(正负号代表风速方向)。

表2 脉动风风速概率分布统计

3 脉动风下弓网离线特性

3.1 脉动风对弓网受流影响

接触网系统在脉动风作用下发生抖振，影响行车可靠性。通过对某段铁路弓网接触压力进行动态仿真，得到不同风速下接触压力，见表3。

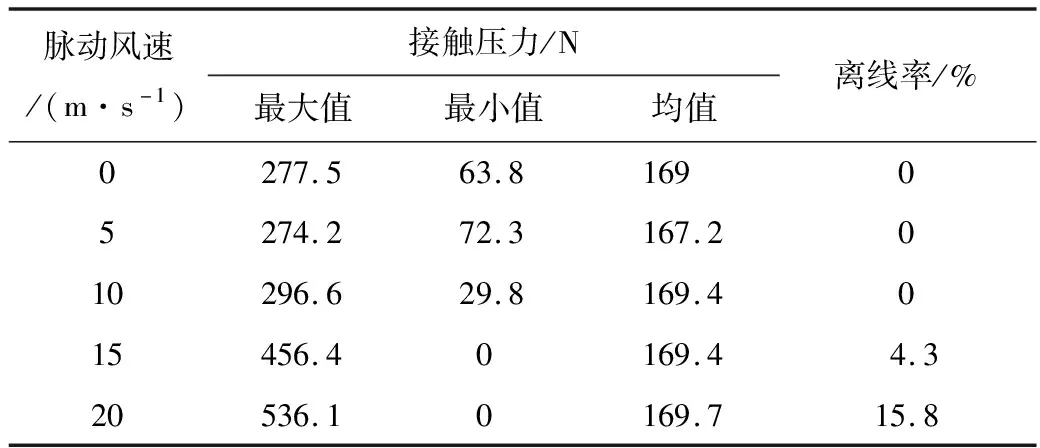
表3 不同风速下接触压力

由表3可知，当脉动风速大于10 m/s时，弓网间接触压力明显增大；当风速为20 m/s时，接触压力差值为536.1 N，离线率15.8%，将影响行车安全。

3.2 脉动风下弓网离线故障率

不同脉动风速下离线率不同。分别计算不同脉动风速下弓网离线率，见表4。

表4 脉动风下弓网离线率

4 脉动风下接触网系统可靠性分析

传统接触网系统可靠性研究没有将西北地区大风运行环境因素考虑在内，导致可靠性计算结果与实际偏差较大。因此，本文将脉动风下弓网离线故障率纳入接触网系统可靠性分析指标，并对其可靠性进行分析。

4.1 高速铁路接触网系统可靠性模型建立

接触网系统主要由6部分串联组成：接触悬挂装置、定位装置、支持装置、附属悬挂、补偿装置以及支柱与基础装置等[11]。

本文采用GO-FLOW法进行接触网系统可靠性分析[12]。GO-FLOW法由日本学者在GO法基础上提出，是1种新的可靠性分析方法[13-14]。

首先根据接触网系统结构，以接触网能够正常运行为导向，建立计及脉动风下弓网离线因素接触网系统GO-FLOW图，如图3所示。其中A、B、C、D、E、F分别表示接触网6个组成部分，M表示脉动风下弓网离线因素，箭头信号流代表接触网系统可靠度。操作符25、21、35分别表示信号制造单元、接触网6个组成部件以及随时间发生失效的工作单元。假定P、Po分别表示操作符本身固有故障率及输出故障率；R、Ro为操作符固有稳定性及相应传递稳定性；Pi、Ri为输入操作符信号故障率及可靠度。则每个操作信号计算逻辑：

图3 计及脉动风下弓网离线的接触网系统GO-FLOW图

1)25号操作符即信号制造单元，其输出可靠性大小和故障可能性，如式(10)～(11)所示：

R=Ro

(10)

P=Po

(11)

2)21号操作符代表2个状态单元，其输出信号和故障率如式(12)～(13)所示：

Ro=Ri+R

(12)

Po=Pi+P

(13)

3)35号操作符代表随时间失效的工作单元，若失效单元故障率为常数K，则其输出可靠度与故障率如式(14)～(15)所示：

Ro=Rie-Kt

(14)

Po=Pie-Kt

(15)

式中：t为持续时间，s；e为常数。

4.2 接触网系统可靠度计算

接触网系统GO-FLOW图共包括21个操作符，根据文献[15]得到接触网系统各组成单元操作符可靠性参数，见表5。

表5 接触网系统各组成单元操作符可能性参数

利用GO-FLOW计算规则得到接触网系统GO-FLOW图对应信号流强度，见表6。

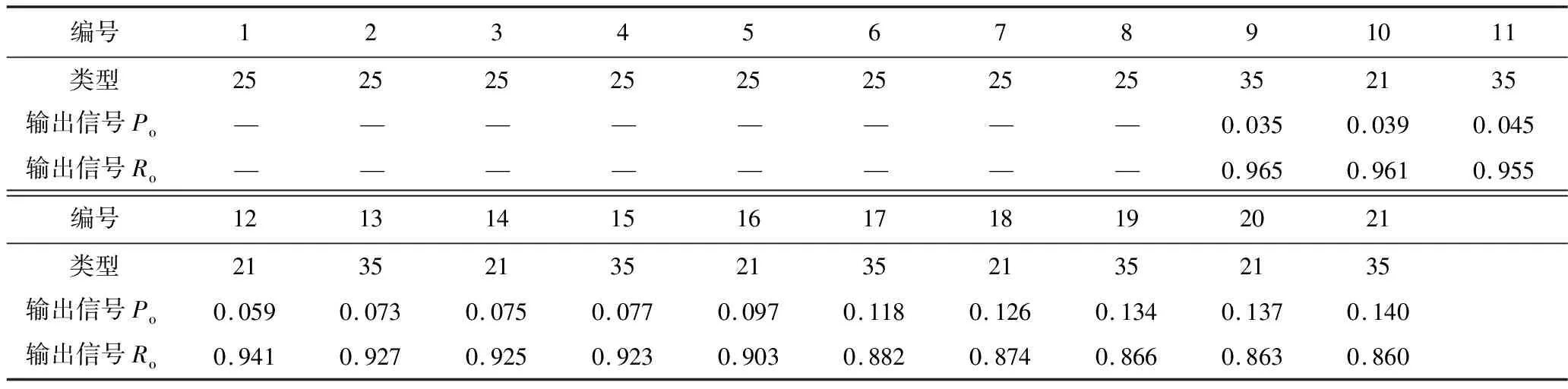
表6 接触网系统GO-FLOW图中信号流强度

4.3 接触网可靠度对比分析

对比考虑脉动风前后接触网可靠度计算结果，如图4所示。由图4可知，当未考虑脉动风因素时，接触网系统最终可靠度R=0.896；考虑脉动风时接触网系统最终可靠度R=0.860，相差3.6%，且脉动风下弓网离线故障率为0.026，与接触网系统某些部件故障率相当。因此，对大风区接触网系统可靠性分析时，必须考虑脉动风对弓网离线影响。

图4 考虑脉动风前后接触网系统可靠度对比

通过对西北地区接触网故障数据统计可知，初步设计阶段可以通过增加防舞鞭、防风墙等增强腕臂结构和接触线强度，降低脉动风影响作用。

5 结论

1)脉动风风速在10～35 m/s分布概率高达29.82%，需有针对性采取防风措施，例如增设防舞鞭等。

2)考虑脉动风下弓网离线影响，接触网系统可靠度略有下降，且故障率高达0.026，与接触网系统组成部件故障率相当，严重影响列车运行安全。

3)为满足高速行车需求，保障列车安全运行，需从多方面着手解决西北风区脉动风影响，例如改进接触网配件性能、定期对接触网系统进行检修维护以及对接触网关键设备服役状态进行监测与预警。