城市供水管网漏损动态预测的Bootstrap-Lee-Carter模型*

王 威，丛 旭，武佳佳，马东辉

(北京工业大学 城市建设学部，北京 100124)

0 引言

为减少管网失效事件发生，提高城市供水管网韧性，诸多学者在对城市供水管网爆管率，漏点率以及剩余寿命进行大量预测工作，对城市安全具有重大意义。

管道破损的影响因素较多，Barton等[1]将其归纳为3大类：管道本身性质；环境因素；运行因素。

王圃等[2]将方差—协方差优选组合模型应用于对给水管网年漏损件数的预测并进行实例分析，结果表明组合模型具有较高的预测精度；邱云龙[3]针对给水管网漏损特点，用方差-协方差优选组合模型将灰色GM(1,1)模型、二次指数平滑模型、自回归移动平均模型应用于漏损频率的预测，提高单个模型的预测精度；王丽娟等[4]在此基础上结合漏点数的季节性周期特点，建立基于差分自回归移动平均模型的管网漏损预测模型。

基于管道自身性质的漏损模型预测方面，Kang等[5]根据GRA的主要程序，对城市供水管网基本渗漏数据进行处理，结果反映与渗漏有较大关系的前3个因素为管径、管道压力以及深度；包涵等[6]同样利用灰色模型对管道漏损率进行预测，得出使用等维灰色模型相比传统灰色模型和无偏灰色模型进行供水管网漏损率预测效果更好；王志红等[7]针对城市管网漏损率数据的非线性和随机波动性特点，建立以马尔可夫链修正灰色GM(1,1)的预测模型，比较分析灰色和灰色马可夫链预测结果，指出经马尔可夫链修正后的模型预测精度更高。

除了以上几种预测方法，国内外学者还从神经网络理论出发在管道漏损率的预测中进行应用分析。Dongwoo等[8]采用主成分分析(PCA)和人工神经网络(ANN)用于估计配水管网中的漏水量，并通过Z评分法获得标准化数据，设计并证明PCA-ANN方法比单个ANN模拟更准确地估计泄漏率；邵圆媛[9]在常规BP神经网络模型基础上，结合平行拓扑结构和最小均方误差识别模式，构建单因素的嵌套GMS神经网络模型用来进行管网的漏损预测；汪健[10]在人工神经网络理论基础上，通过对小波变化的研究，建立小波神经网络模型对供水管网的压力及管道进行预测研究。

综上，国内外学者目前针对供水管网漏损方面均进行了卓有成效的研究，但是在相关讨论过程中，目前关于管网漏损率的研究方法大多数停留在静态分析阶段，刘晓然等[11]应用动态分级方法对管网漏损分类分级控制，但并无预测由于时变因素对管网漏损率的影响，所以本文在Lee-Carter模型[12]的基础上结合曾燕等[13]选用的Bootstrap方法，充分考虑Lee-Carter模型所有参数的变动性，对昆明市某供水管网的漏点率进行动态分析，以便弥补静态分析模型的不足。

1 供水片区管网概况

基于前期调研资料[14]，截止到2016年，昆明市某片区供水管网约413 km，2016年平均日供水量约1.46×104m3，供水面积约106 km2，并供约36.2万人口使用。不同管径和管材管道占比统计如表1所示，不同管材管道占比统计如表2所示。

表1 不同管径管道统计情况

表2 不同管材管道统计情况

2 Lee-Carter模型动态分析及其参数估计

2.1 模型简介

以供水管网的管龄时间作为影响管道漏点率的主要影响因素，Lee-Carter模型如式(1)所示:

lnmx,t=ax+bxkt+εx,t

(1)

式中：mx,t为t年管径/管材为x的管道漏点率；kt为依赖于时间t的参数；ax为依赖于管径/管材的参数；bx为各管径/管材漏点率对kt的敏感度；εx,t为误差项。

(2)

式中：c为任意常数。

对模型参数进行归一化处理，如式(3)所示：

(3)

式中：t为年份；T为年份总数；x为管径或管材。

Lee-Carter模型预测供水管网漏损预测实现步骤：1)通过往年漏点率数据估计参数ax，bx，kt；2)通过ARIMA方法得到kt在未来的预测值；3)将kt及ax,bx代入模型，以获得漏点率的预测值。

2.2 参数估计

1)最小二乘法(OLS)

基于Lee-Carter模型的假设，如式(4)所示：

(4)

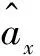
将式(1)两边对管径/管材x进行求和，如式(5)所示：

(5)

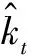
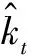
(6)

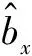
2)加权最小二乘法(WLS)

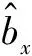
(7)

式中：dx,t为管道漏点数。

2.3 数据与拟合结果

采用OLS和WLS对该片区供水管网数据分析，可得不同管径管道的Lee-Carter模型参数的估计值，如图1所示。不同管材管道的Lee-Carter模型参数的估计值如图2所示。kt值整体上变化幅度较小；ax代表管道的中心漏点率，随着管径增大漏点率减小；从bx的波动可以看出，小管径管道对时间因子的敏感度较低，大管径管道对时间更为敏感。

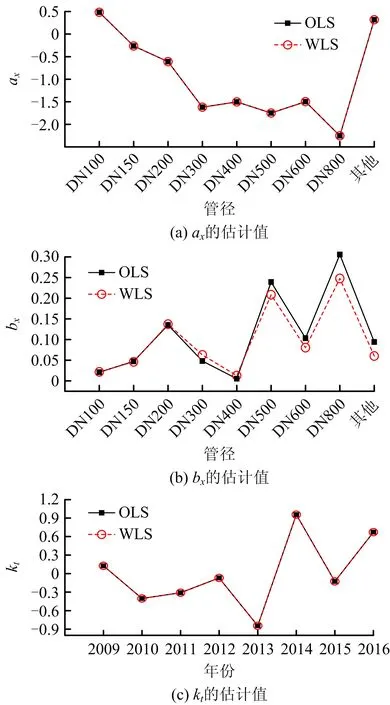
图1 不同管径管道经典模型的参数估计值

针对球墨铸铁管(DIP)、灰口铸铁管(GCIP)、钢管(SP)、PE管(PEP)和水泥管(CP)进行模型参数估计，由图2可知，2种估计方法得到的管材kt值整体上变化幅度比较小；ax的参数值反映出，DIP的管道漏点率较低，其余5种管材类型的管道均具有较高的漏点率；DIP，PEP和CP受时间因子影响较小，而GCIP和SP受时间因子影响较大。

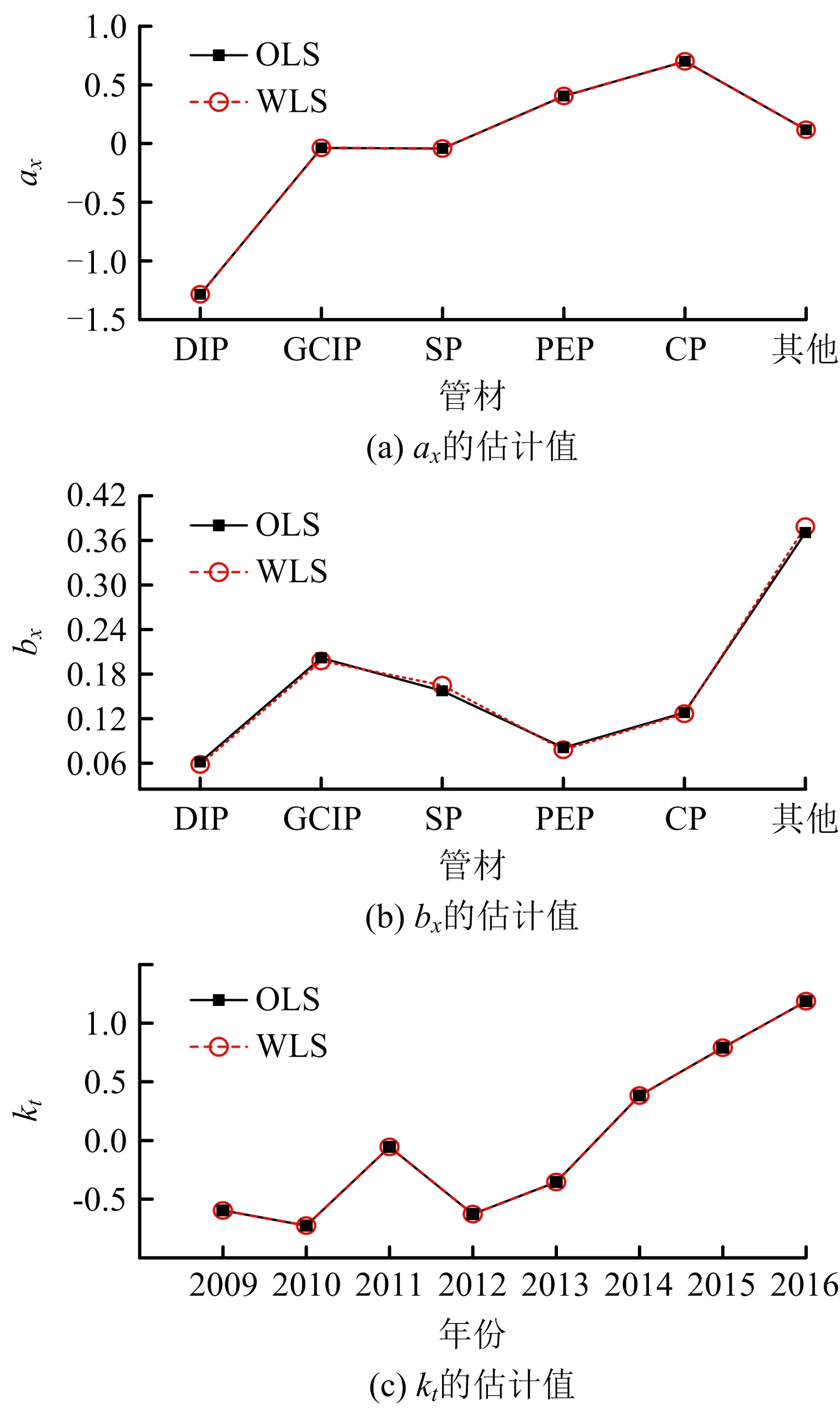
图2 不同管材管道经典模型的参数估计值

在2种参数估计方法中，OLS假设残差独立同分布；WLS假设残差独立，但方差与管道漏点数有关。为检验2种方法的残差是否满足各自的残差假设，可根据参数估计时做的分布假设对2种方法残差进行修正。若残差的分布假设成立，则修正后的残差应具有明显的独立同分布性。因此修正后残差的独立同分布性质可用来判别这2种估计方法的优劣。

根据式(1)可知，OLS估计的残差假设为独立同分布，因此不用对残差进行修正，如式(8)所示：

(8)

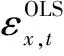
WLS的残差平方以管道漏点数作为权重，因此定义其修正后的残差，如式(9)所示：

(9)

利用MATLAB编程，可得到不同管径管道的残差等高线图如图3所示，不同管材管道的残差等高线图如图4所示。从图3中管径的残差等高线图中可以看出OLS和WLS均具有一定的聚集特性，而图4中管材的残差等高线图都表现出了较好的随机性。本文采用Levene方差齐性检验方法[15]对其进行分析，结果如表3所示。

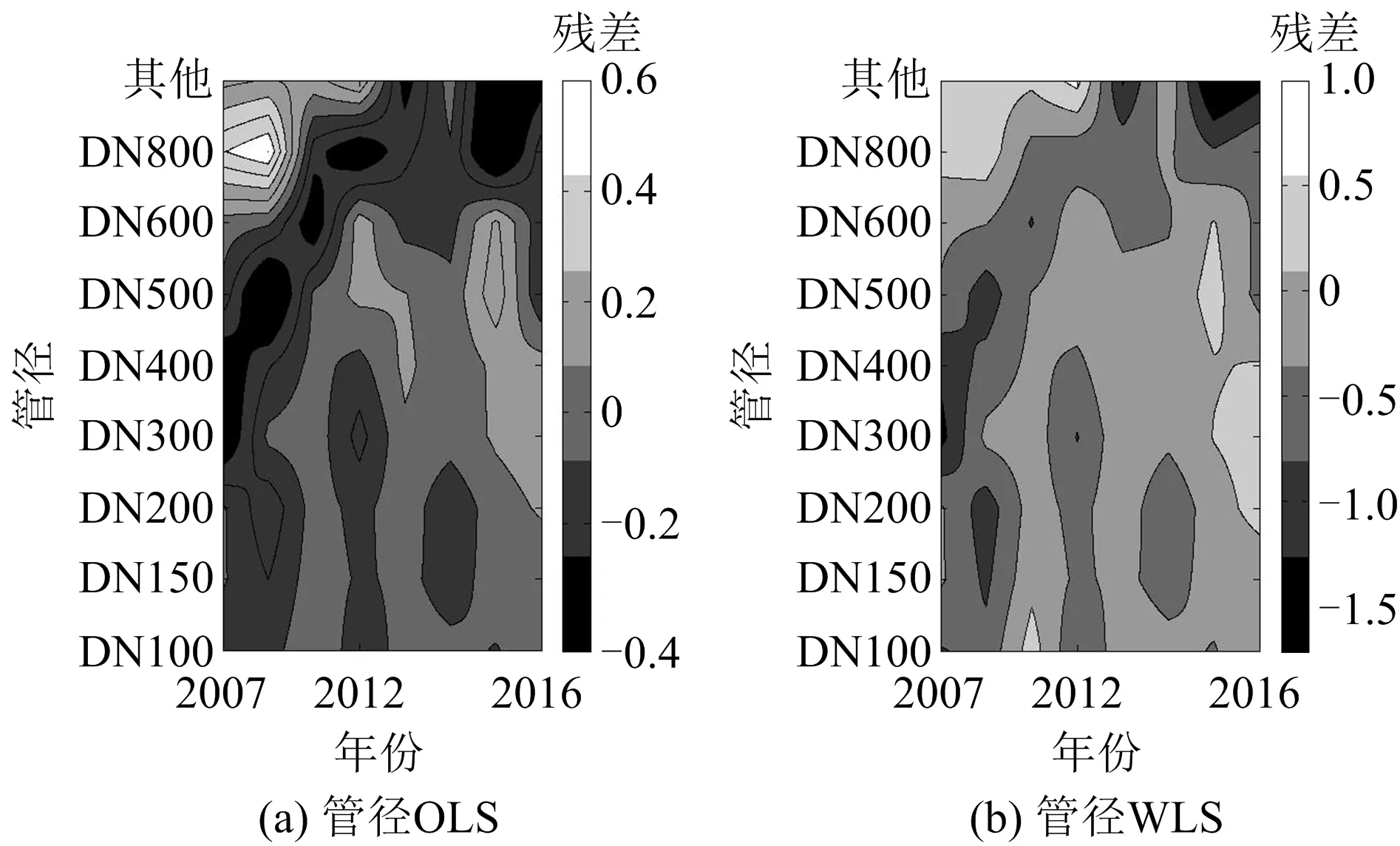
图3 不同管径管道的2种参数估计方法的残差等高线

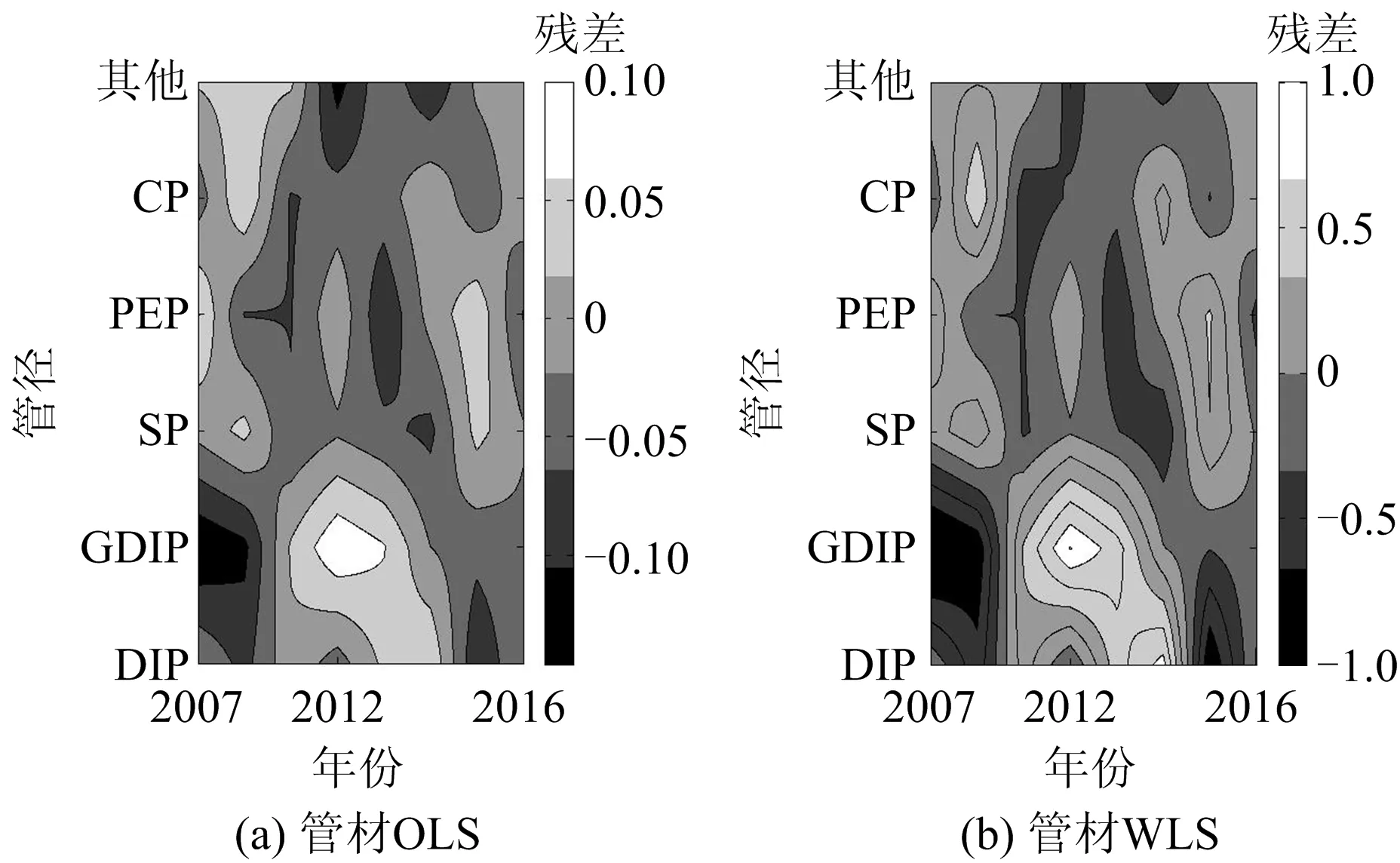
图4 不同管材管道的2种参数估计方法的残差等高线

基于Levene检验的参数值如表3所示。可知，无论按照管径类别或管材类别，还是按照年龄，F>P，即第1列都大于最后1列，说明接收H0，不接受H1，不同方差齐性，各个样本方差不相同。考虑时间因子，WLS的p值更大，结合残差等高线图，综合考虑WLS作为参数的估计方法更优。

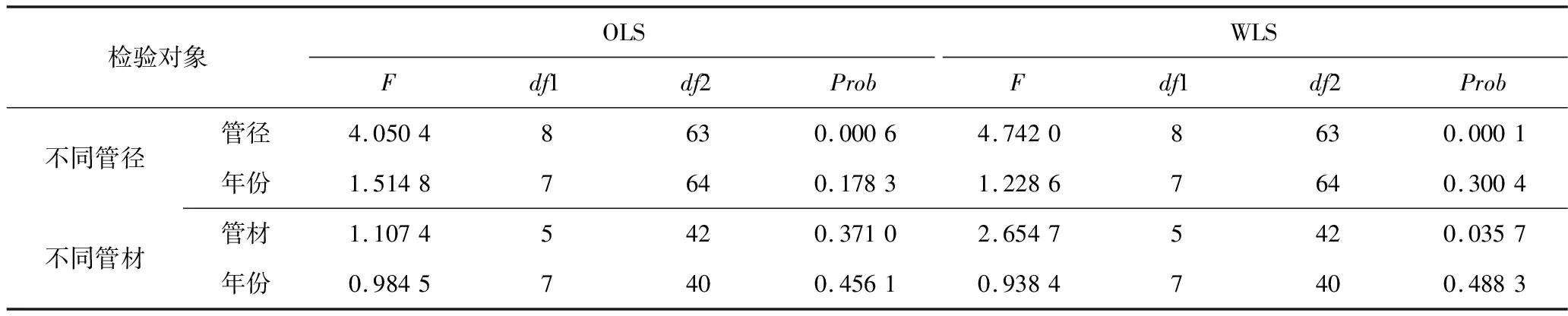
表3 基于Levene检验参数值

3 经典Lee-Carter模型预测管道漏点率

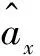
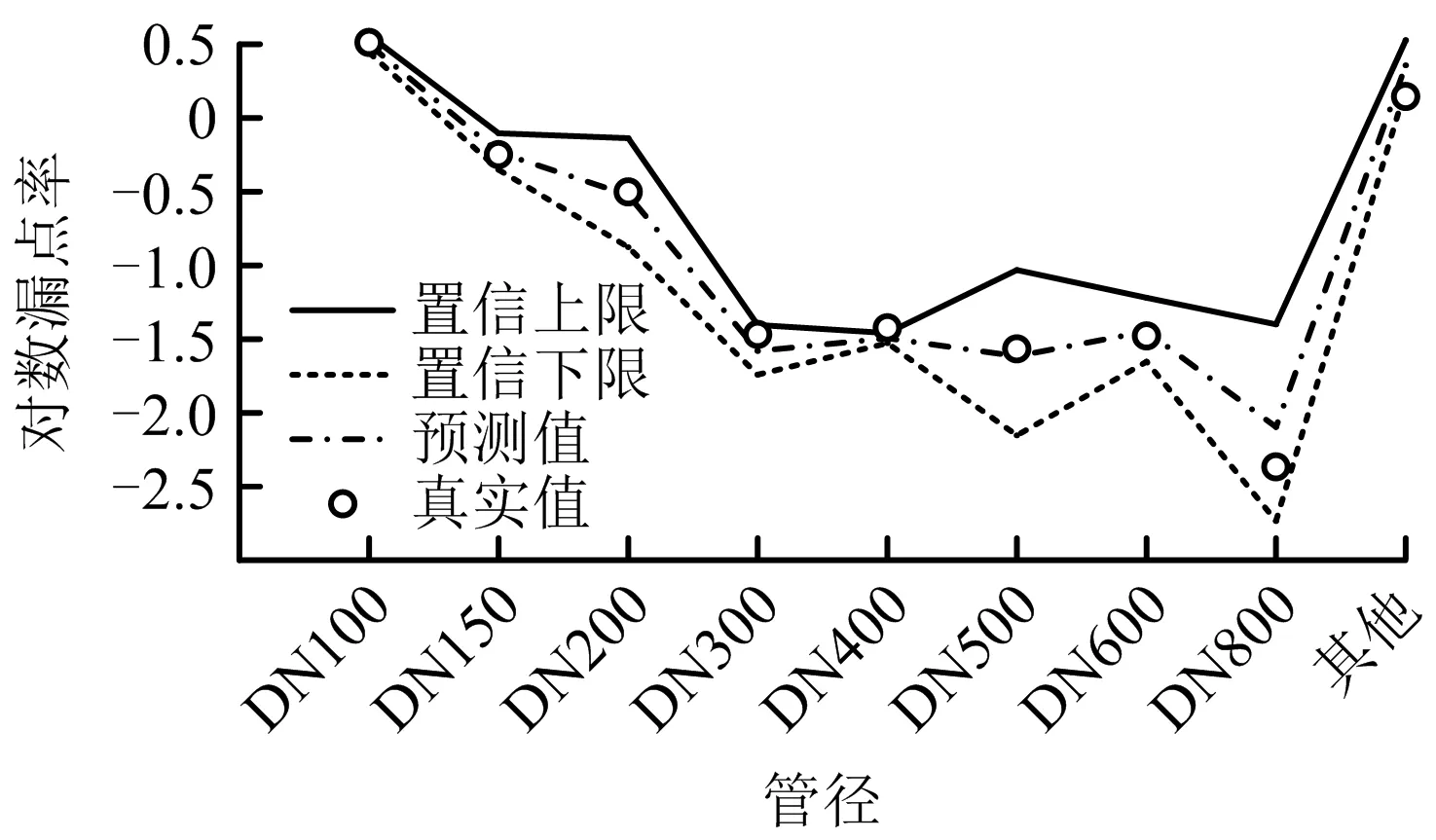
图5 2017年不同管径管道漏点率预测值置信区间

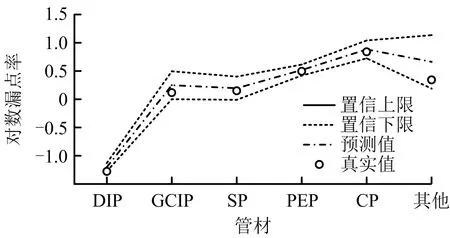
图6 2017年不同管材漏点率预测值置信区间

由图5和图6可知，供水管道漏点率预测值的置信区间并不太准确，原因在于传统的Lee-Carter模型没有考虑其他2个参数ax，bx的变动性。而Lee-Carter模型不能通过传统的检验方法对参数进行检验，其参数的分布不能由已知的分布函数进行描述，因此可结合Bootstrap方法对模型参数进行估计，并计算参数及漏点率的置信区间。

4 结合Bootstrap方法预测漏点率

以传统Lee-Carter模型作为漏点率预测模型，基于Bootstrap方法计算参数置信区间的稳健性，同时在考虑所有参数变动性的基础上预测未来漏点率的置信区间。具体实现步骤如下[13]：

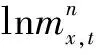
(10)

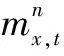
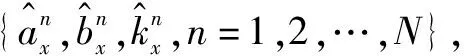
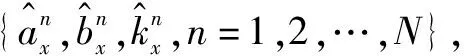
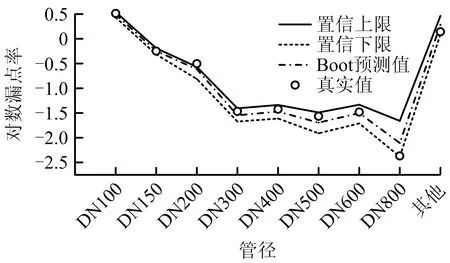
图7 2017年不同管径管道Bootstrap漏点率预测值置信区间

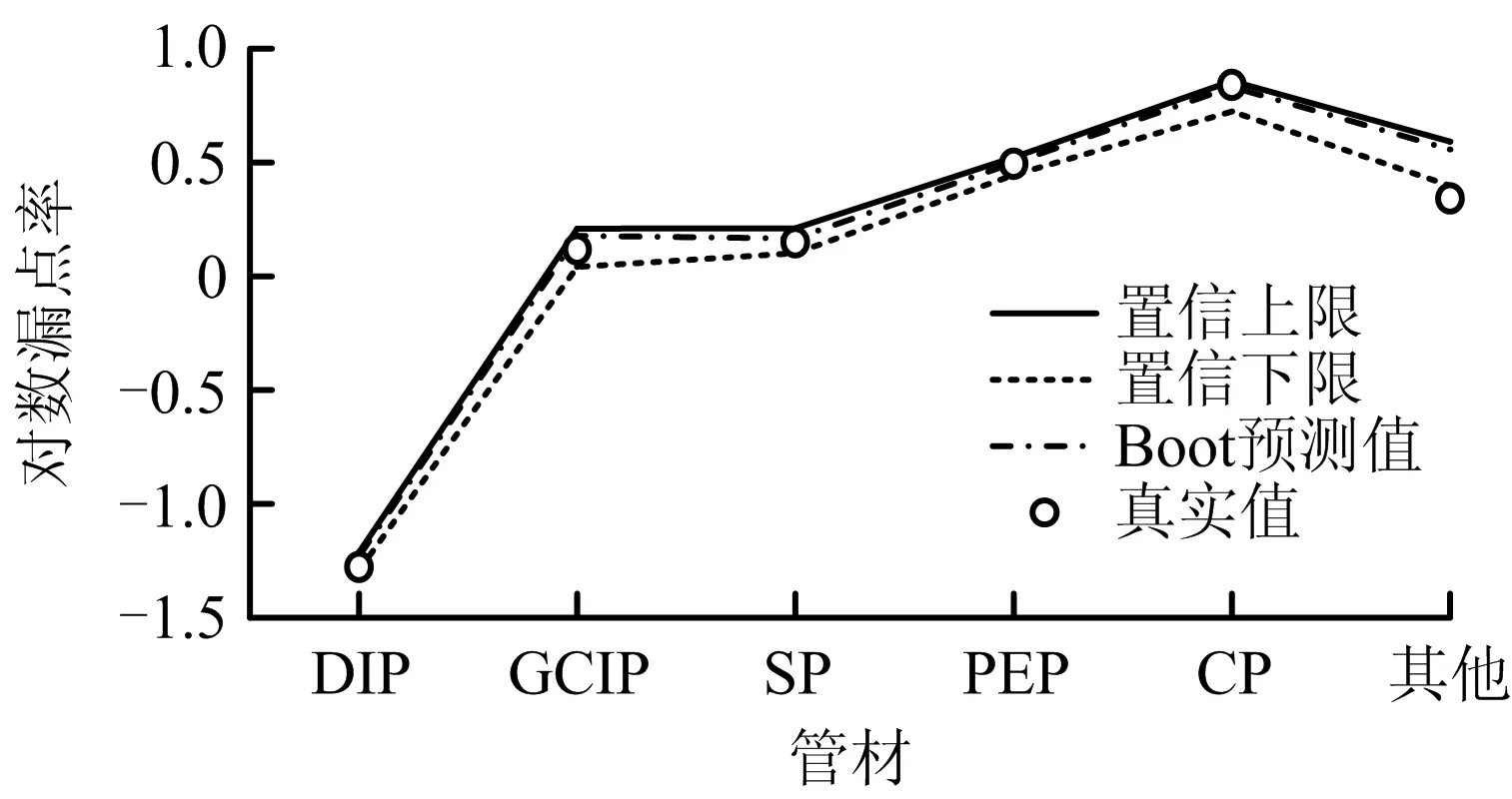
图8 2017年不同管材管道Bootstrap漏点率预测值置信区间

将2017年不同管径以及不同管材的管道Bootstrap预测的漏点率预测与实际的漏点率进行对比，误差统计如表4所示。

由表4可知，DN800的管道的预测值和实际值之间误差较大，其余管径类型误差较小，这是由于大管径管道实际漏点率较低，计算相对误差时作为分母较小，导致误差增大，但就漏点率本身而言，预测值与实际值接近。对于不同管材的管道，计算结果显示其他管材类型的管道误差稍高，主要考虑到种类较多，因而漏点数的累积值较大，但预测值与实际值接近。

表4 2017年的Bootstrap漏点率预测值误差统计

综上，结合Bootstrap方法的Lee-Carter模型预测管道漏点率在精度上有较大提高，拟合效果贴近实际情况。

5 结论

1)基于Lee-Carter模型对昆明市某供水片区的管道漏点率进行拟合与预测，分析得到加权最小二乘法的残差具有较好的独立同分布性质。结果表明，利用Bootstrap方法预测的管道漏点率置信区间能够包含真实的漏点率，具有较高的精度。

2)从分析结果可以得到影响管道剩余寿命的2个危险因子——管龄和管径：管道的年限越长，管径越小，管道剩余寿命愈短，即管道的漏损率越高。在城市供水管网系统中，为避免爆管事故的频繁发生，需要采取针对性措施降低管道的渗漏风险，延长管道经济剩余寿命。