基于多重平衡体系的索辅梁拱桥设计

马振栋，姚 龙，闫福成

(林同棪国际工程咨询(中国)有限公司，重庆 401121)

拱桥是所有桥梁体系中最富于变化的结构，现代拱桥不仅向大跨径发展，也向造型多样化发展，如斜靠式拱桥、蝴蝶拱等空间异形拱桥应用越加广泛[1-2]。拱桥尽管形态各异，结构上大多属于大跨径缆索承重桥梁[3]，即主拱和吊索是提供整体刚度及承载受力的主要结构，梁体主要起提供局部刚度、传递活载的作用。当今城市建设中，常要求结合城市整体设计和景观需求，把桥梁建成能反映该城市历史文化、人文风貌等地标性或景观性的桥梁[4]，这类桥梁的典型特征是：1)桥面较宽，常在40 m以上；2)因造型要求较高，常出现异形或非对称形态的结构。随着梁拱组合体系桥梁的发展,特别是邓文中院士在2007年提出“以充分发挥梁体自身承载能力为前提，把缆索设计成辅助受力结构”的索辅梁桥设计理念[5-7]，使拱的形体更轻型化，为造型丰富的异形或非对称拱结构设计创造了条件。非对称且与多吊索面结合的空间异形组合拱桥的构造及受力均较复杂，可参考的研究成果及设计经验较少。为此，本文以前海合作区11号景观桥为例，采用索辅梁桥的理念和多重平衡体系的分析思路，阐述此种组合体系拱桥达到理想状态，即“面内受力平衡、面外受力平衡、梁体横向受弯平衡”的分析过程，对利用分析成果优化后的结构在使用状态下的受力性能进行评价，并对异形组合拱桥的设计做出总结、给出建议。

1 多重平衡体系设计思路

异形或非对称形态拱结构的拱轴线不是抛物线、悬链线等规律性很强的曲线[8-9]，拱肋常为倾斜及设有多吊索面布置。多重平衡体系的设计思路，就是在利用吊索的布置位置、角度、吊索力调整等方式，将吊索的合力调整到拱平面内，并将拱轴线向吊索合力的压力线靠拢及重合[10]，使异形或非对称形态的拱结构达到平衡的受力状态，具体可按下述过程思考及分析。

1)面外受力平衡状态

采用多索面倾斜布置的拱肋，自重G产生的外倾力会造成拱的面外受弯，需吊索F1与F2形成的合力F3，与拱平面形成一个恰当的反向角度(F3与F4间夹角)来平衡；平衡拱结构自重产生的外倾力，G与F3的合力F4位于拱肋的平面内，使拱达到面外受力平衡状态，如图1(a)所示。

2)面内受力平衡状态

面内结构非对称的拱肋，根据吊索S1～Si在拱肋上的布置特点，吊索需相应倾斜地布置，使拱轴线尽量与压力线重合，达到面内受力平衡的状态，如图1(b)所示。

3)梁体横向受弯平衡

多索面锚固于梁体横向不同位置，如图1(a)所示，为超宽型桥面在竖向提供多点支撑，减小梁体横向弯曲受力。

(a)平衡示意1

2 工程概况

深圳前海合作区11号景观桥，简称11号桥，为下承式非对称索辅梁拱桥，桥梁主跨80 m，全宽53 m。该桥以高低拱喻山、以结构流动的线条比水、以非对称布置代表城市融合，满足了突出“山、水、城”三元素的景观要求，设计效果图如图2所示。

图2 桥梁实景

受路线高程和通行游船的要求，主梁限高为2.0 m、高跨比1/40，采用分离式钢箱梁结构，并用多道横梁连接为整体，在中分带处镂空。根据索辅梁桥的理念，采用跨度经验公式：

(1)

式中：L辅为采用缆索辅助后可达到的跨径，m；L梁为该梁体用在梁式桥时的跨径，m；K为综合系数；η为梁体的承载比。该桥K=1，L辅=80 m，L梁=50 m，算出η=0.4，得到η缆索=1-0.4=0.6，即缆索只需承担60%的荷载效应，故采用轻型化的钢拱结构设计。

高低拱均为正六边形钢箱截面，在桥梁平面内为非对称布置，拱脚于A1台处分设在两边人行道的内侧，于A0台处收拢并均设于中分带，如图3(a)、(b)所示。高低拱在自身平面内均为非对称结构，高拱拱顶向A0台处偏移9.12 m，低拱拱顶向A1台处偏移2.12 m。高低拱的面外倾斜角受车行道通行界限的限制，约在垂直～外倾10°间具有布置条件；两拱均采用双吊索面稀索布置，也只有在拱的上半部分才具有设置条件，如吊索均匀设置在该区域，如图3(c)中虚线所示，则会造成严重的空间割裂感，影响行车视觉。因此，吊索以2 m为间距集中布置在拱顶局部区域，在梁体上均集中布置在对单跨结构最有效的跨中1/3桥长区域，横向上分别锚于人行道内侧及中分带。

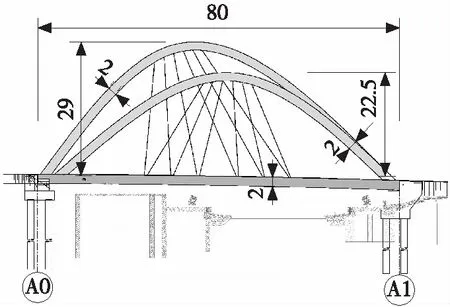
(a)立面布置

3 平衡体系分析

3.1 桥梁有限元建模

为研究该桥体系的受力过程，采用有限元程序Midas Civil对全桥建模。将主梁及横梁离散为纵横向网格单元,采用三维梁单元模拟；高低拱肋采用三维变截面梁单元模拟；吊索采用只受拉桁架单元模拟。为准确反映受力情况，构件截面特性均按实际结构取值，考虑变形中的P-Δ效应[11]，模型共646个节点、880个单元，如图4所示。施加的静力荷载包括自重、二期恒载，汽车及人群活载，并以移动荷载方式施加，考虑整体及局部温度效应，按设计规范取值[12]。

图4 有限元模型

3.2 面外受力平衡影响分析

对于宽度53 m且中分带镂空的梁体，4个索面在横桥向为梁体提供均匀一致的竖向支撑对其受力最有利。因此，以梁体横向受弯平衡为基本目标，在此条件下，拱肋采用垂直于平面还是倾斜布置对拱的面外受力影响较大。为此，在其它结构参数不变的情况下，分别研究高低拱的倾角对拱肋受力的影响，以确定结构影响的敏感性及应力的变化规律。拱脚、1/4拱及拱顶处这3个特征位置，常为弯矩最大或受弯曲影响最敏感的位置[13-14]，且随着倾角的变化其结果变化较大，因此将这3个位置的应力作为3个控制目标来研究其受力变化。以拱平面的夹角0°～10°变化作为研究范围，计算出控制目标随着角度变化的取值，从而得出一系列的控制点并用图形表示，经分析比较得出变化规律，并对11号桥高低拱的合理外倾角取值给出建议。

3.2.1 高拱应力的变化规律

高拱的拱脚、1/4拱、拱顶处应力的变化规律如图5所示。

由图5可知：1)恒载作用下(成桥状态)，高拱的拱脚处应力受倾角变化影响显著，即拱肋面外弯曲效应受倾角变化影响显著，且在拱脚处为极大值，在倾角0°～10°变化时呈现出应力逐渐增大的趋势，增速较快，整体上应力增加了28 MPa；对1/4拱及拱顶处应力均影响微弱，应力变化在4 MPa之内；高拱恒载下总体应力水平为60 MPa～93 MPa；2)活载作用下，对3个位置均影响微弱，整体上应力变化在3 MPa之内，总体活载应力水平为21 MPa～38 MPa，约为恒载的1/3，说明梁体的刚度较大，是主要承重结构，高拱的吊索及拱肋辅助受力作用较为明显；3)使用状态标准组合下，3个控制目标呈现的变化规律与恒载作用下规律一致；高拱的应力水平为102 MPa～127 MPa，达到JTG D64—2015《公路钢结构桥梁设计规范》[15]中应力允许值210 MPa的49%～60%，应力结果比较理想，说明按以梁体横向受弯平衡为基本目标，有条件达到高拱面外受力平衡的目的，为优化高拱面外受力，其外倾角度应尽量取较小值。

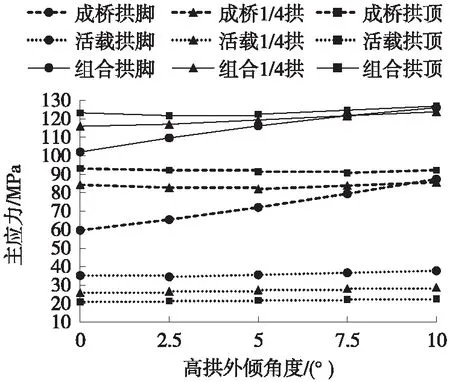
图5 高拱应力的变化规律

3.2.2 低拱应力的变化规律

低拱的拱脚、1/4拱、拱顶处应力的变化规律如图6所示。

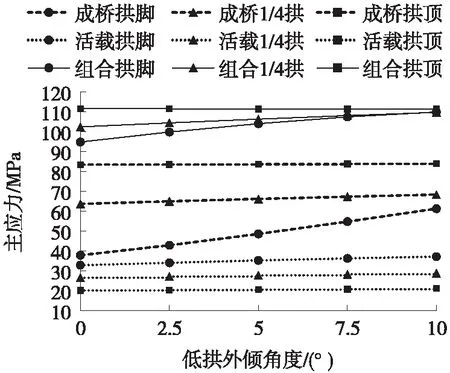
图6 低拱应力的变化规律

由图6可知：1)恒载作用下(成桥状态)，低拱的拱脚处应力受倾角变化影响显著，即拱肋面外弯曲效应受倾角变化影响显著，且在拱脚处为极大值，在倾角0°～10°变化时呈现出应力逐渐增大的趋势，增速较快，整体上应力增加了23.4 MPa；对1/4拱及拱顶处应力均影响微弱，整体上应力变化在4.3 MPa之内，低拱恒载下总体应力水平为 38 MPa～84 MPa；2)活载作用下，对3个位置均影响微弱，整体上应力变化在2.5 MPa之内，总体活载应力水平20 MPa～37 MPa，约为恒载的40%，同样说明梁体为主要承重结构；3)使用状态标准组合下，3个控制目标呈现的变化规律与恒载作用下规律一致；低拱的应力水平为95 MPa～111 MPa，达到规范应力允许值的45%～53%，应力结果比较理想，说明按以梁体横向受弯平衡为基本目标，可以达到低拱面外受力平衡的目的，为优化低拱面外受力，其外倾角度也应尽量取较小值。

11号桥，因受车行道通行界限的控制，高低拱的倾斜角度在0°(即拱面垂直于桥面)时，拱结构的外轮廓刚好与界限角点重合。为适当留出安全距离，高低拱均取外倾2.5°时，可保证结构与界限角点有20 cm的额外安全距离，因此选用外倾2.5°作为高低拱的倾角值。

3.3 面内受力平衡影响分析

高低拱在自身平面内均为左右非对称结构，吊索也是呈非对称斜向布置的特点，如图3(a)所示。在以梁体横向受弯平衡为基本目标，且吊索在桥面处及拱上布置位置基本确定的条件下，高低拱的拱轴线是否合理对拱的面内受力影响较大。因此，在高低拱外倾角度取2.5°，且其它结构参数不变的情况下，分别研究高低拱的拱轴线对拱肋受力的影响，以确定结构影响的敏感性及应力的变化规律，并以拱脚、1/4拱、拱顶处的应力作为3个控制目标。

拱轴线对比示意如图7所示。由图7可知，因空间及异形拱的拱轴线不是规则曲线，无法用方程描述，故高低拱的面内拱轴线以“接近于三角刚架”向“接近于圆弧”的规律取5条编号为1号～5号的拱轴线作为研究范围，即每2条曲线间1/4点处弓高差为0.5 m～0.6 m，计算出控制目标随着拱轴线变化的取值，得出一系列的控制点并用图形表示，经分析比较得出变化规律，并对11号桥高低拱的合理拱轴线给出建议。

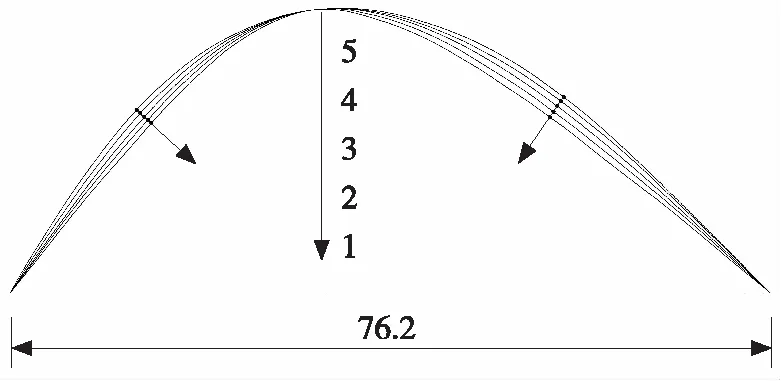
(a)高拱面内拱轴线

3.3.1 高拱应力的变化规律

高拱的拱脚、1/4拱、拱顶处应力在不同拱轴线下的变化规律如图8所示。

由图8可知：1)恒载作用下(成桥状态)，高拱的拱脚、1/4拱、拱顶处3个位置均受拱轴线变化影响显著，尤以1/4拱处最为显著，拱轴线1号～5号的变化过程中均呈现出应力直线增大的趋势，且增速较快，应力增幅分别为30 MPa、57.6 MPa、39 MPa，高拱恒载下总体应力水平为53 MPa～113 MPa；从变化曲线可见，高拱的拱轴线呈现出越接近于三角刚架形态拱肋应力越小的趋势，反映出集中在拱顶局部区域且斜向布置的吊索形成的压力线趋向于三角刚架的形态；2)活载作用下，3个位置受影响均较为敏感，拱轴线1号～5号的变化过程中均呈现出应力直线增大的趋势，但增速较慢，应力增幅分别为7.3 MPa、14 MPa、8.5 MPa，总体活载应力水平14 MPa～37 MPa，约为恒载的1/4～1/3；3)使用状态标准组合下，3个控制目标呈现的变化规律与恒载作用下规律一致；5条拱轴线所得的高拱应力水平为76 MPa～154 MPa，达到规范应力允许值的50%～73%，高拱面内受力可控，说明按以梁体横向受弯平衡为基本目标，有条件达到高拱面内受力平衡的目的，为优化高拱面内受力，拱轴线应尽量向接近于三角刚架的形态取用。

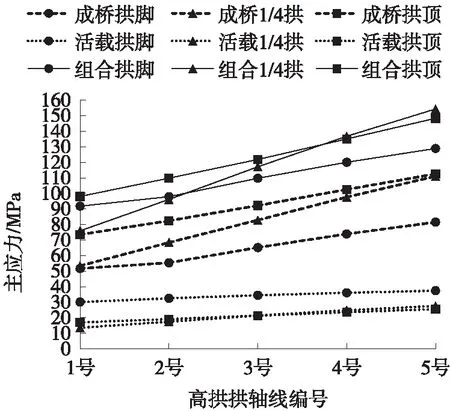
图8 高拱应力的变化规律

3.3.2 低拱应力的变化规律

低拱的拱脚、1/4拱位置、拱顶处应力在不同拱轴线下的变化规律如图9所示。

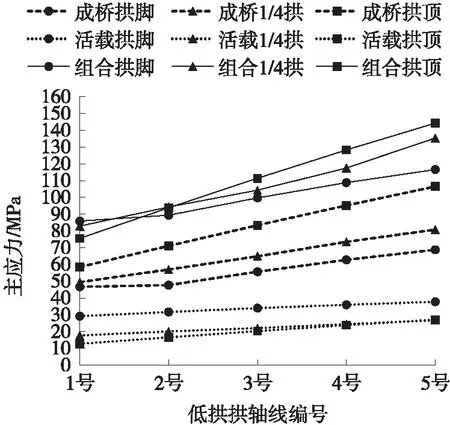
图9 低拱应力的变化规律

由图9可知：1)恒载作用下(成桥状态)，低拱的拱脚、1/4拱、拱顶处3个位置均受拱轴线变化影响显著，尤以拱顶处最为显著，拱轴线1号～5号的变化过程中均呈现出应力直线增大的趋势，且增速较快，应力增幅分别为22 MPa、31.3 MPa、48 MPa，低拱恒载下总体应力水平50 MPa～107 MPa；从变化曲线可见，低拱的拱轴线也呈现出越接近于三角刚架形态拱肋应力越小的趋势，反映出集中在拱顶局部区域且斜向布置的吊索形成的压力线趋向于三角刚架的形态；2)活载作用下，3个位置受影响均较为敏感，拱轴线1号～5号的变化过程中均呈现出应力直线增大的趋势，但增速较慢，应力增幅分别为8.6 MPa、9 MPa、14.4 MPa，总体活载应力水平13 MPa～38 MPa，约为恒载的1/3；3)使用状态标准组合下，3个控制目标呈现的变化规律与恒载作用下规律一致；5条拱轴线所得的高拱应力水平为76 MPa～144 MPa，达到规范应力允许值的50%～69%，低拱面内受力可控，说明按以梁体横向受弯平衡为基本目标，也有条件达到低拱面内受力平衡的目的，为优化低拱面内受力，拱轴线也应尽量向接近于三角刚架的形态取用。

由本节分析可知，高低拱最优的拱轴线均为尽量向趋近于三角刚架的形态取用。对11号桥车行道通行界限分析可知，在高低拱的拱轴线过分地向三角刚架的形态逼近时不能满足其要求，故高低拱均取3号曲线作为设计拱轴线，可满足拱肋与界限角点有20 cm的额外安全距离。

综上分析，对11号桥高低拱进行优化，均选用外倾2.5°作为倾斜值，均选用3号拱轴线进行拱肋设计，并对Midas Civil程序所建的有限元模型进行对应的修改，在标准荷载组合下分析所得的主要结论如表1所示。

表1 全桥关键位置内力、应力

由表1可见，主梁应力发挥充分，符合索辅梁桥的设计前提；横梁受拉及受压应力基本一致且均较小，吊索力比较均匀，以梁体横向受弯平衡为目标设立正确；高低拱应力在满足规范的前提下，应力相对较小，主要以轴向压应力为主，基本达到了面内受力平衡和面外受力平衡的状态，多重平衡体系设计思路及方法正确，结构受力状态较为理想。

4 结束语

通过对11号桥这种典型的“在布置及结构上均为非对称且与多吊索面结合”的空间异形组合拱桥的理想受力状态论述分析及验证过程，总结出对该类桥梁设计方法的建议为：

1)通过优化拱面倾斜角度和吊索面角度，在平衡拱肋的横向倾斜受力后将拉索的合力调整到拱肋平面内，使布置上非对称的拱肋达到面外受力平衡的状态。

2)结合吊索在拱上及梁上的布置特点优化拱轴线设计，将拱轴线向吊索合力的压力线尽量靠拢及重合，使面内结构非对称的拱肋达到面内受力平衡的状态。

3)超宽型扁平梁体可利用多索面锚固于梁体横向不同位置,为其在竖向提供多点支撑，减小梁体横向弯曲受力，达到横向受弯平衡的状态。

4)索辅梁桥的梁体自身刚度较大，辅助作用的吊索在纵桥向需设在跨中区域等最有效的位置，与非对称空间异形拱组合时，可达到梁、索、拱三者协同受力的效果。

5)多重平衡体系这种使拱结构达到“面内受力平衡、面外受力平衡、梁体横向受弯平衡”的设计思路，是分析“非对称空间异形拱桥”的有效手段，具有参考意义。