显化科学方法教育 发展学生科学思维
——以 “正交分解法”复习为例
2021-07-12徐汉超李俊永王长江
徐汉超 李俊永 王长江
(1. 江苏省苏州市吴江中学,江苏 苏州 215200;2. 贵州省仁怀市周林高级中学,贵州 仁怀 564500;3. 安徽师范大学物电学院,安徽 芜湖 241002)
1 引言
高中物理教学因其自身的特殊性,在发展学生科学思维方面具有不可替代的作用。遗憾的是高中物理教育在这些方面的工作难以令人满意,具体表现在一些高中生的物理问题解决能力弱,不能有效地运用科学方法解决具体的物理问题,学生的科学思维能力较弱。鉴于此,笔者提出:物理教学活动应该围绕学生的思维活动而展开,通过显化科学方法的策略来发展学生的科学思维。
物理教育家阎金铎、乔际平先生在《高中物理:概念·规律·方法》中,从力学到电磁学的各个单元分别对科学方法教育进行了分析与说明,邢红军教授也提出了科学方法中心论、显化科学研究方法等观点,《普通高中物理课程标准(2017年版)》将“科学思维”作为核心要素的四个方面之一。
科学思维贯穿于问题解决的全过程,笔者认为科学方法的教育在适当时机需要显化,现以高三“正交分解法”的复习为例,探讨显化科学方法教育、发展学生科学思维的途径。
2 教学案例分析
高三物理教学特别是二轮复习教学更加注重方法的积累与总结,大多数高三学生科学思维能力没有得到较好的发展,究其原因在于他们在高中物理学习中对基本的科学方法不甚了解,笔者采用显化科学方法教育的方式来解决这个问题,从而提升学生的科学思维能力。
2.1 通过对比,引发科学思维
如图1所示,新课伊始呈现最简单的直流电路并截取一个节点上的相应电流,同时展示与之类似的共节点力的示意图,并寻求图1中各量的关系。
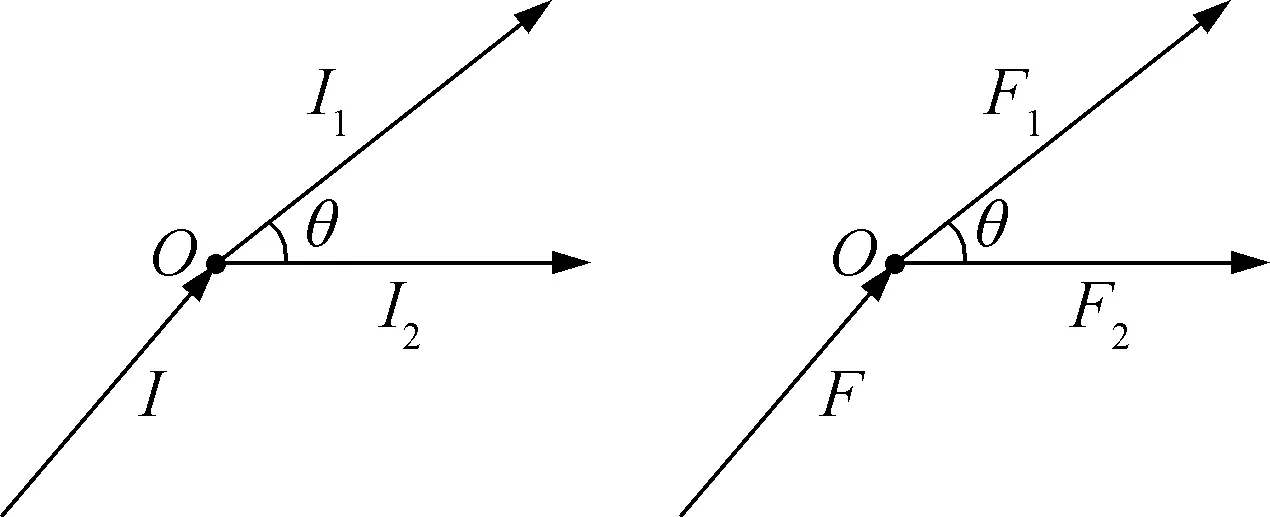
图1
让学生比较电流与力的求和规则,教师提问:I=I1+I2,F=F1+F2是否成立?学生在脑海中调用电流和力的求和规则,判断出这是在考查矢量与标量的本质区别,并确认后一公式错误。教师引出正交分解的问题:怎么才能使矢量的求和简单、便捷?
如图2所示,力的正交分解法是指把力沿着两个选定的互相垂直的方向进行分解,是力的平行四边形定则的具体应用,体现的是等效思维方法。该环节应强调正交分解过程,得出:Fy=Fsinα,Fx=Fcosα。
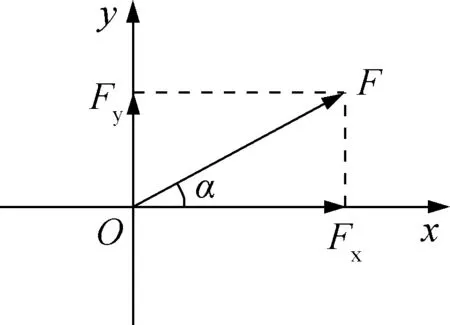
图2
设计意图:通过学生对电流与力节点图的观察,调动学生已有认知,由此启动学生的思维,对两个等式正误的判断会使学生关注物理量的求和规则,进而提出解决力求和的问题,正交分解法呼之欲出。本设计考虑到学生先前知识储备,抓住矢量、标量求和的不同,为正交分解法的复习铺平道路。
2.2 利用分解过程,培育科学思维
运用力的正交分解法解题时需要认真审视具体的物理问题,把握问题的关键特征,正确列出数理方程,显化科学方法的教育。
例1:如图3所示,物体所受重力为G,在与水平方向成α角的恒定拉力F作用下沿水平面匀速运动,求物体与水平面间的动摩擦因数。

图3
解析:运用正交分解法列出竖直方向上和水平方向上的平衡方程,再寻找两个方向上的具体联系,即建立:∑F=0或其分解式∑Fx=0,∑Fy=0,这是正交分解法的精髓。
设计意图:在教学中,学生的能力需要在实践中提高,在练习中提升,该例有利于学生对科学方法的掌握。在正交分解法依次展开的过程中,学生的科学思维能力逐渐提高,并以此为新起点将思维逐步向纵深进阶。
为了让学生对问题的认识更加深刻,也为了很好地发展学生的模型建模、科学推理等科学思维能力,实现思维的纵深进阶,可对例1进行变式处理。
变式1:若恒力向右斜向下,与水平方向夹角不变,物体做匀速运动,求物体与水平面间的动摩擦因数。
变式2:若物体在恒力的作用下产生向右的加速度a,求物体与水平面间的动摩擦因数。
2.3 正交分解牵连速度,拓展科学思维
正交分解也可以根据研究问题的需要拓展到对运动的研究中,正交分解的方向在原则上有无穷多个,但在具体的问题中要根据方便性原则灵活选取。紧接前面的教学,以牵连速度问题为载体的正交分解实例拓展学生的思维。


图4
解析:如图5所示,对小球A和B的速度进行正交分解,再结合系统的机械能守恒解决该问题。其中既有把两小球视为质点的理想化处理,也有对轻杆不可伸长的理想化处理,即沿杆方向A和B的速度相等,也涉及机械能守恒的明确表述,每一步都有科学思维方法的运用。在具体的研究方法上,力可以正交分解,速度亦可正交分解,进而任何矢量皆可正交分解,正交分解法的运用在具体问题中需灵活处理。

图5
设计意图:科学思维能力的发展不能毕其功于一役,只能循序渐进、逐步去落实。从对问题解决的每一个细节的处理来讲,不论是建模还是论证,都需要依据科学方法
教育的要求细化问题,化复杂为简洁。
2.4 在复合场中运用正交分解法,进阶科学思维
带电粒子在复合场中的运动能够较好地体现科学方法的教育价值,利于学生科学思维能力的提升,基于等效方法的正交分解法在复合场中的应用就是一例。
例3:如图6所示,一带电微粒以竖直向上的初速度v0,自A点进入场强大小为E、方向水平向右的匀强电场,微粒受到的电场力重力大小相等,当微粒到达B点时,速度大小仍为v0,但方向变为水平,那么A、B之间的电势差等于多少?从A运动到B经历的时间为多少?

图6
解析:本例比较复杂,带电微粒的运动可以分解为竖直方向上的上抛运动与水平方向上的匀加速直线运动。此外需挖掘隐含条件:B点的速度水平向右,体现了科学论证能力培养的要求,引导学生思考:为什么带电微粒在B点的速度可以水平向右,在A点竖直方向速度为什么会改变?学生会利用正交分解法去分解力和运动,探讨分运动的等时性和独立性问题。
设计意图:在具体的问题解决中显化科学方法教育,首先,准确把握水平方向与竖直方向上的运动具有等时性;其次,具体问题具体分析,在建模过程中把握正交分解法运用的基本要领;再次,以图表形式让思维可视化;最后,对物理问题解决的过程进行反思,通过科学方法的运用实现科学思维进阶。
3 显化科学方法教育的建议
3.1 物理教师应当具有研究和梳理科学方法的意识
显化科学方法并突出其中心地位,需要物理教师特别是物理备课团队深入研究和挖掘课程标准和教材中的科学方法教育因素,有意识地将科学方法在物理课堂中显化出来,物理备课组应重点研讨科学方法显化的具体方式,发挥集体的力量,摒弃单兵作战模式,提高研讨效率。
3.2 在复习中应当以科学方法的运用为关键支撑
物理核心素养的落实最终指向学生的终身发展,知识的复习与掌握离不开有效的实践,此实践主要指学生对与科学方法相联系的物理习题、原始物理问题的解决,日日有进则可至千里,在物理复习中显化科学方法的教育是落实核心素养培养的重要途径。
