基于频率分集逆合成孔径雷达的多重信号分类目标成像算法
2021-07-12贾新迪廖可非欧阳缮
贾新迪, 廖可非,2*, 欧阳缮,2, 杜 毅
(1.桂林电子科技大学信息与通信学院, 桂林 541004; 2.桂林电子科技大学卫星导航定位与位置服务国家地方联合工程研究中心, 桂林 541004)
近年来逆合成孔径雷达(inverse synthetic aperture radar, ISAR)发展迅速,由于其工作不受环境影响且能对远距离目标进行高分辨成像,在众多领域都得到了广泛应用[1-2]。目前ISAR成像系统大都采用宽带相控阵雷达系统,通过发射宽带信号来获得高的距离向分辨率,然而宽带相控阵天线系统的工程实现难度较大[3]。文献[4-5]首次提出了频率分集阵列,它是一种由相控阵演变而来的新体制雷达阵列;文献[6]分析了频率分集阵列的波束特性,并通过仿真进行了验证;文献[7]将频率分集的思想应用在ISAR成像技术中,形成了频率分集ISAR成像新体制,解决了宽带信号发射接收复杂的问题。但是频率稀疏导致了旁瓣的提高[8],并且在有较强噪声环境下,使用传统成像算法[如后向投影(back projection, BP)算法],成像效果不是很好,对于目标的识别有很大干扰。
多重信号分类(multiple signal classification, MUSIC)算法使空间谱估计技术迎来了新时代。MUSIC算法的工作原理是将阵列接收数据的协方差矩阵进行特征值分解,得到两个正交子空间,即信号子空间和噪声子空间,然后利用正交性来构成空间扫描谱,从而对信号参数进行估计[9-11]。文献[12]将MUSIC算法应用在频率分集阵列上,通过发射-接收多组不同频率增量的雷达信号,可实现波束距离-角度解耦,以此对目标进行定位;文献[13-14]则对比了对数频率增量、三角函数频率增量、随机频率增量等非线性频率增量对目标成像的不同影响;文献[15]提出了一种新的基于Toeplitz矩阵重构的波达方向估计算法,提高了空间谱中信号与噪声的区分度以及传统算法在进行波达方向估计时的精度。
基于此,现提出了一种基于频率分集ISAR的MUSIC成像算法,该方法采用随机倍频频率增量,将得到的不同频偏情况下合成阵列接收的回波信号协方差矩阵进行特征值分解,得到信号子空间与噪声子空间,利用两个空间的正交性构造谱函数对应用场景进行扫描,完成距离-方位的联合估计,从而获得目标的超分辨二维像。
1 系统模型
主要针对平稳飞行的目标,即目标的运动可视为匀速直线运动,频率分集ISAR模型几何结构图如图1所示。

图1 成像系统几何结构Fig.1 Geometric structure of the imaging system
当目标移动时,雷达在不同观测时刻t向目标发射不同频率的单频信号f,在tn时刻,雷达的发射频率为
fn=f0+mnΔf,n=0,1,…,N-1
(1)
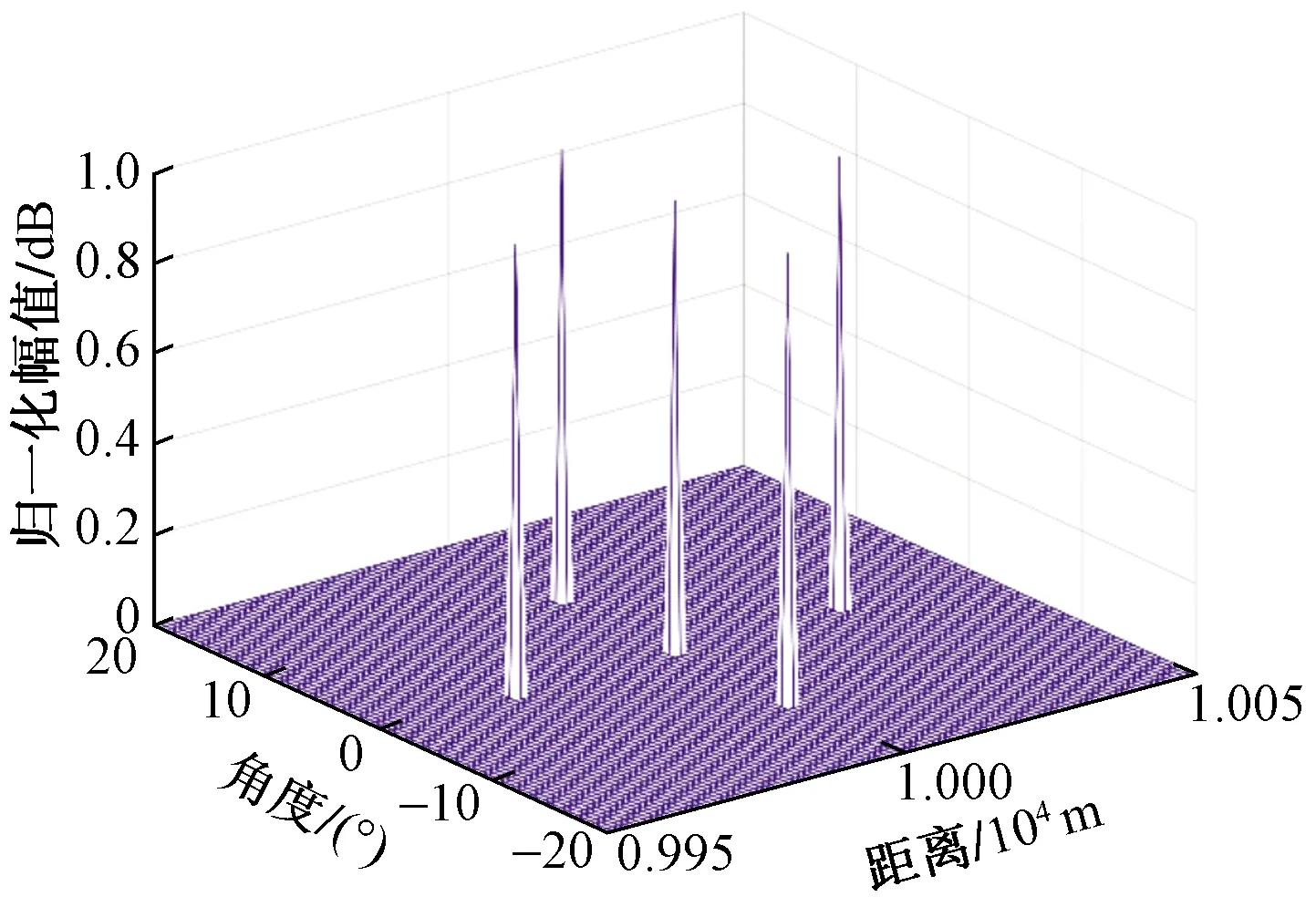
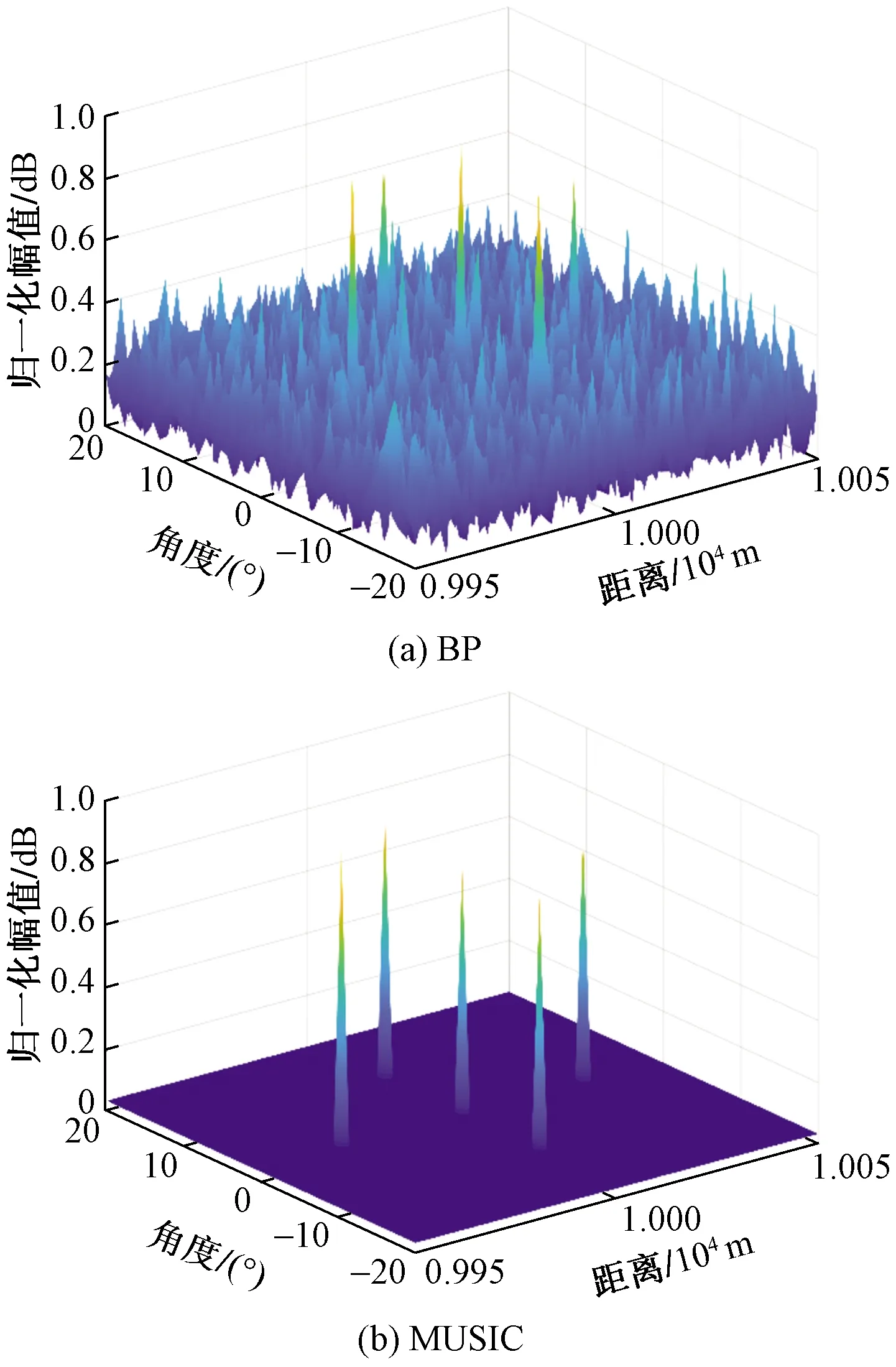
式(1)中:f0为阵列初始发射频率;mn=rand(n)表示从[0,N-1]中随机选取一个数;Δf表示频率增量,满足mnΔf< 目标飞行过程中,会产生平动和转动两个分量,如图2(a)所示,为简化分析,假设雷达和目标位于同一平面,雷达到目标中心的初始距离为R0,且目标以V0作径向运动,以ω做转向运动,tn时刻雷达到目标上某一散射点p的距离为Rp(tn),现以目标中心为原点O建立直角坐标系XOY,如图2(b)所示。 设目标上有一散射点p,在t0时刻该散射点位于p0(x0,y0)处,与X轴的夹角为θ0。当t=tn时刻该散射点将运动到一个新的位置pn(xn,yn),此时该散射点相对于X轴的夹角为θ(tn)=ωtn+θ0。ρ为该散射点到原点的距离。则t=tn时刻散射点pn(xn,yn)到雷达的距离可表示为 ω为目标转动角速度;V0为目标径向运动速度图2 目标与雷达的几何关系Fig.2 Geometric diagram of target and radar Rp(tn)= (2) 在远场条件下,式(2)中[R0+V0tn+ρcos(θ0+ ωtn)]2>>[ρsin(θ0+ωtn)]2则有 Rp(tn)≈R0+V0tn+ρcos(θ0+ωtn)= R0+V0tn+xncos(ωtn)-ynsin(ωtn) (3) 在tn观测时刻,雷达的发射波形可以表示为 x(tn)=s(tn)exp(j2πfntn),n=0,1,…,N-1 (4) 式(4)中:fn为tn时刻雷达发射频率;s(tn)为信号的复包络。某散射点p的回波信号xe可表示为 xe(tn,p)=s[tn-2Rp(tn)/c]× exp{j2πfn[tn-2Rp(tn)/c]} (5) 式(5)中:c为光速;由于发射信号是单频信号,因此s(tn)的变换相对比较慢,可得s[tn-2Rp(tn)/c]≈s(tn)。另将接收到的回波信号与exp(j2πfntn)混频后,则p点回波信号变为 xe(tn,p)=s(tn)exp{-j2πfn[2Rp(tn)/c]} (6) 在tn时刻所有散射点的回波信号可表示为 (7) 式(7)中:P为散射点个数。 雷达在不同的观测时刻发射不同频率的单频信号,目标与雷达在不同的观测时刻会产生相对位置变化,因此在成像算法中,对不同频率、不同距离的目标回波进行相位补偿后,再相参累加,可同时对距离向、方位向成像。 (8) 在第1节中,已得到tn时刻所有散射点的回波信号xe(tn,P),将其与相位补偿矩阵Φtn相乘,得到回波矩阵Atn(x,y)=xe(tn,P)Φtn,最后将N个进行时延补偿后的回波矩阵相参累加,获得目标二维像为 (9) 由第1节可知,第n个观测时刻的雷达多散射点回波信号模型可以写为 (10) 假设目标散射点个数P A(x,y)S(t) (11) 式(11)中:S(t)=[s1(t),s2(t),…,sP(t)]T;A(x,y)=[a(x1,y1),a(x2,y2),…,a(xP,yP)],其中任意一项a(xp,yp)可表示为 (12) 式(12)中:Δθ为相邻两个观测时刻目标转过的角度。 考虑各观测时刻的噪声,阵列接收矢量可以表示为 X(t)=AS(t)+N(t) (13) 式(13)中:N(t)=[n1(t),n2(t),…,nN(t)]为噪声矢量,其中nN(t)为均值为0,方差为σ2的相互独立的白噪声。回波矩阵的自相关函数被定义为 R=E[XXH]=ARSAH+σ2I (14) 式(14)中:E[·]表示求期望;[·]H表示复共轭转置运算;RS=E[SSH]表示信号S的协方差;I为N×N阶单位矩阵。对自相关矩阵R进行特征值分解,划分为信号子空间和噪声子空间,即 (15) 式(15)中:ΣX为P个大特征值构成的对角阵,其对应的特征向量构成信号子空间UX;ΣN为N-P个小特征值构成的对角阵,其对应的特征向量构成噪声子空间UN。 最后构造谱函数PMUSIC,并在空间MUSIC频谱上搜索峰值的位置来估计每个散射中心的具体位置,即 (16) 假设目标以200 m/s的速度做匀速直线运动,雷达等时间间隔对目标观测241次。雷达发射信号初始频率f0=10 GHz,频率增量Δf=1 MHz,频率增量采用随机倍频的形式。成像过程中目标相对于雷达转过的角度范围为-20°~20°,将5个目标点分别设置在(0°,10 km),(0°,9.97 km),(0°,10.03 km),(10°,10 km),(-10°,10 km),假设目标散射系数为1,目标场景图如图3所示。 图3 目标场景图Fig.3 Target scene diagram 首先用BP算法对目标场景进行仿真实验,可以得到仿真图(图4)。 重点比较在噪声存在的情况下,两种不同算法成像效果的区别,因此假设加入的噪声为彼此独立的零均值高斯白噪声,图5、图6分别为在信噪比SNR=10 dB,SNR=-10 dB情况下,两种不同算法的成像结果。 图4 无噪声BP仿真图Fig.4 Noiseless BP simulation diagram 图5 目标成像结果 SNR=10 dBFig.5 Target imaging results SNR=10 dB 图6 目标成像结果SNR=-10 dBFig.6 Target imaging results SNR=-10 dB 从仿真结果可以看出,在频率分集ISAR体制下,BP算法和MUSIC算法都可以对运动目标完成二维成像,随着噪声的增大,算法估计性能都有所下降。另外在噪声强度一样的情况下,BP算法的目标成像旁瓣更高,在噪声达到一定值时,目标信号强度易被淹没在噪声里,而导致目标无法被分辨出来。MUSIC算法相比于BP算法的成像效果更好,每个散射点处仍能形成最大增益,与其他非散射点位置有较明显的对比度,说明本文所提的MUSIC算法在有较强噪声情况下也能有较好的成像效果。 将单频信号合成宽带信号,可解决现有逆合成孔径雷达成像系统发射接收宽带信号复杂等难点,但由于频率稀疏,传统的成像算法带来了旁瓣提高等问题,因此研究基于频率分集ISAR成像体制的MUSIC算法,采用随机倍频频率增量,在雷达接收到回波信号协方差矩阵后,将其进行特征值分解,得到信号子空间与噪声子空间,再利用二者的正交性构建谱函数对目标场景逐点扫描计算,完成距离-方位的联合估计,实现对目标的二维成像,通过仿真结果分析,可得出以下结论。 (1)频率分集ISAR体制可通过单频信号合成宽带信号,解决系统发射接收宽带信号复杂的问题,但由于频率稀疏,带来旁瓣提高等难点。 (2)采用BP算法可对目标进行成像,但随着噪声的增大,旁瓣也逐渐增高,噪声达到一定强度时,目标将无法被分辨出来; (3)采用MUSIC算法在对运动目标进行二维成像时,可有效降低旁瓣,在有较强噪声情况下,目标点处仍能形成最大增益,从而实现对目标的成像与定位。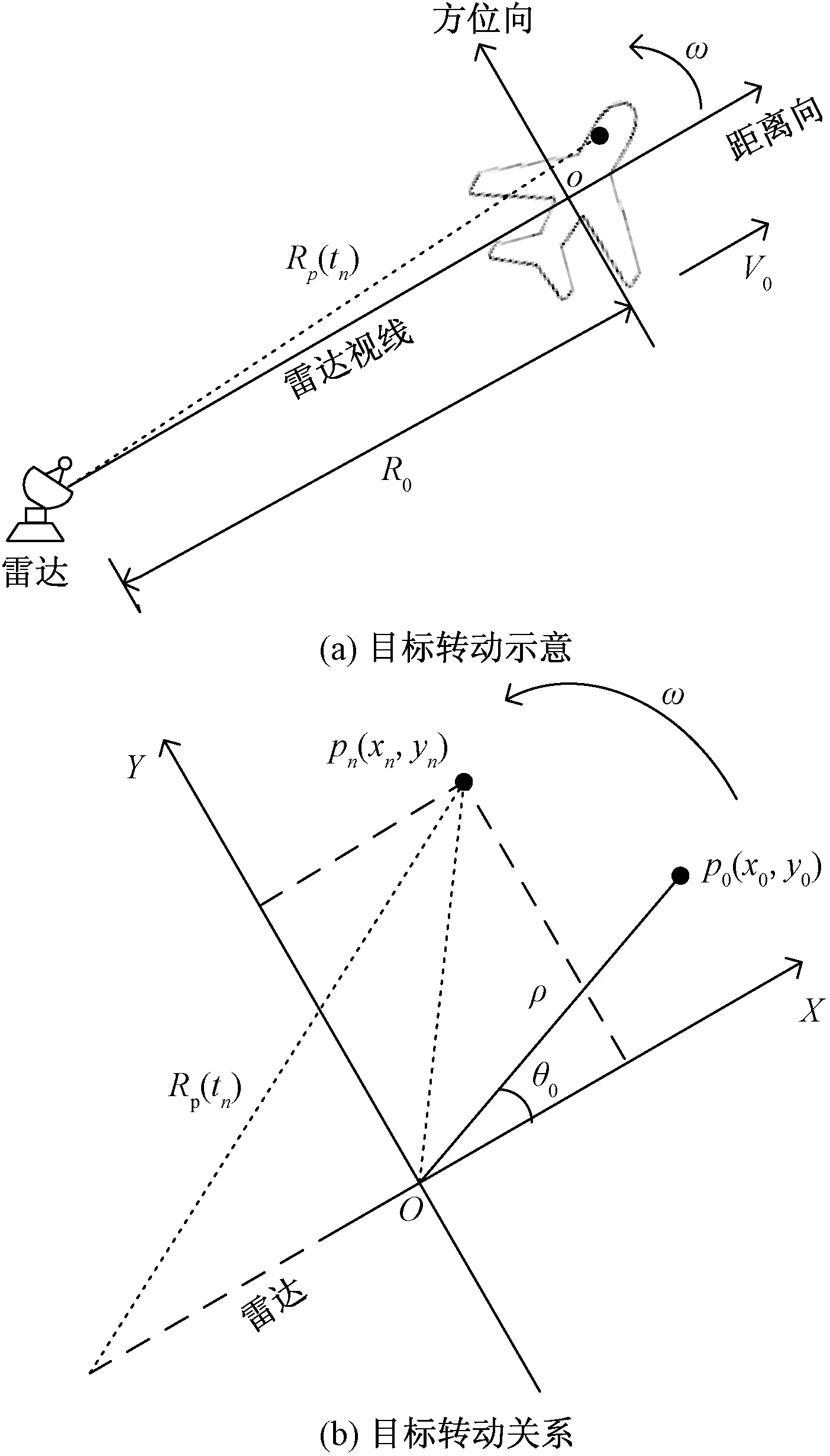


2 成像方法
2.1 后向投影算法

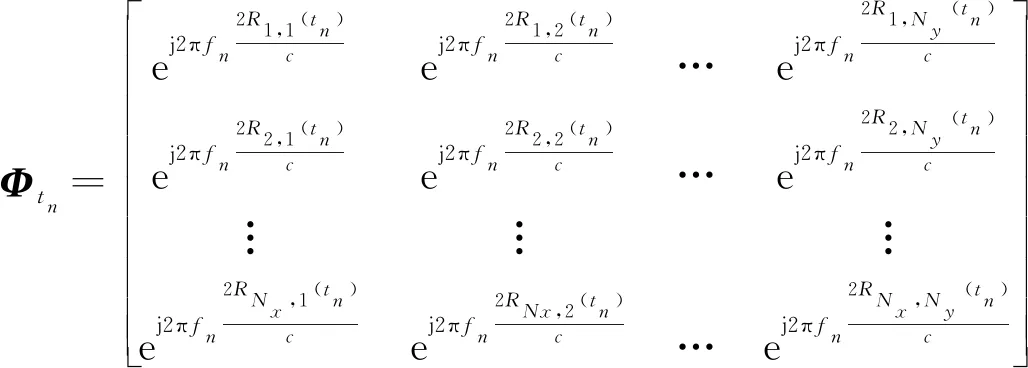

2.2 MUSIC算法

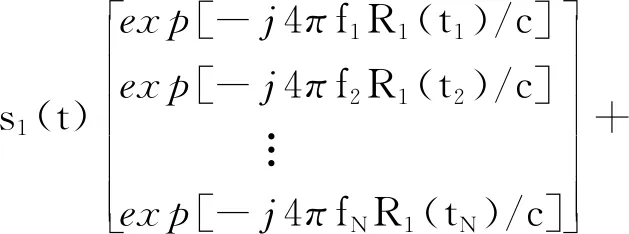
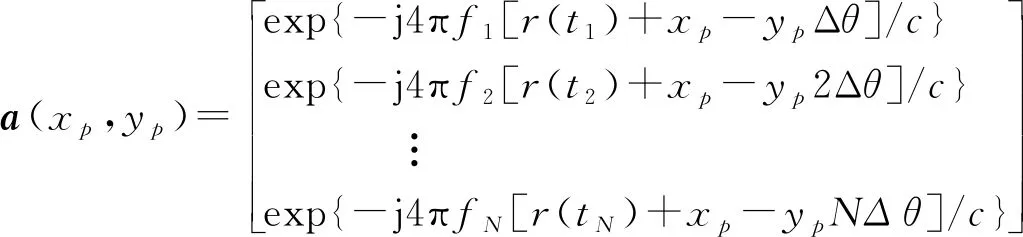

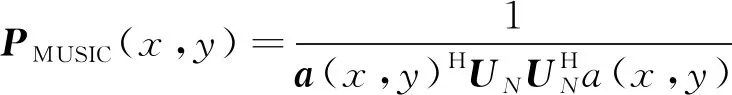
3 实验仿真
3.1 实验场景设计
3.2 不同算法仿真比较


4 结论
