飞机起落架动力学建模及地面运动仿真
2021-07-12唐瑞琳
唐瑞琳, 巩 磊, 王 博
(航空工业第一飞机设计研究院飞控系统设计研究所, 西安 710089)
在飞机研制的过程中,需要在飞行模拟器上进行飞行品质评估试验以评价飞行品质,并在后期培训飞行员以降低试飞风险。除空中飞行外,飞行模拟器还需要在飞机滑跑、离地、触地阶段能准确地模拟飞机的地面运动特性,提供给飞行员真实的起降感受。由于地面存在支反力和摩擦力,飞机在空中和地面的受力情况有着本质区别,不仅导致飞行员在空中和地面的操纵方式不同,对于电传飞机而言,一般也是依据起落架承载情况,切换飞控系统控制律的逻辑或结构。因此对起落架动力学模型的要求不仅是起着地面支反作用,而是应尽可能地精准。特别对于螺旋桨飞机,由于螺旋桨同向旋转引起不对称滑流,地面滑跑时会受到滑流和气动的侧力,需要飞行员通过偏转转向轮(或方向舵)进行纠偏,因此需要正确描述起落架在横侧向的受力情况,才能反映飞机地面运动特性。这对起落架动力学模型精准度的要求更加严格。由于无人机自主滑跑仿真的需要,通过对无人机起落架的建模[1]可用于分析无人机特定的自主滑跑仿真[2-7]及转弯操纵分析[8]。
由于起落架结构、受力、工况复杂,通过建立虚拟样机在ADAMS环境中仿真是一种行之有效的起落架系统设计手段[9-13],但飞行模拟器具有高实时性要求,因此虚拟样机的方法不适用。在以往起落架实时仿真模型中,起落架结构和受力的简化和假设造成了一定的局限性。杨春生等[14]所建立的起落架动力学模型只限于特殊姿态的解算;Sun等[15]只在二维对称平面建立了起落架动力学模型;苏彬等[16]建模假设了起落架前轮转向轴垂直安装并忽略机轮倾侧效应;徐冬苓等[17]和徐世玥[18]忽略了起落架的侧向受力;张雯等[19]独立计算机轮和缓冲器受力导致受力不平衡;袁东[20]未考虑俯仰姿态对机轮触地判断的影响且着陆时缓冲器压缩量高频振荡。
为了建立能真实仿真飞机任意状态的地面运动特性的起落架动力学模型以更好的评价飞行品质和培训飞行员,首先提出极坐标结合坐标转换的方法计算每个起落架机轮的触地点并得到承载情况,然后推导缓冲器压缩行程和压缩速率的代数计算方法,再分析得到机轮在空间的滚动方向定义,从而解析得到精准的侧向摩擦,并利用相互作用力原理在不忽略缓冲器应力的基础上解算出缓冲器受力及地面摩擦力,最后得到所有起落架相对于飞机的力和力矩,用于飞机运动参数解算,从而可模拟飞机任意状态下的地面运动。
1 模型结构
飞行模拟器飞行仿真模型的原理是将飞机的气动、发动机和起落架在飞机体轴系下的力和力矩代入到体轴系下的运动方程进行统一解算,得到飞机运动参数。为了将起落架模型与仿真模型集成,起落架模型计算的结果应该是当前状态下在飞机体轴系下的力和力矩,如图1所示。

图1 起落架动力学模型与飞行动力学模型的关系Fig.1 The relationship between landing gear dynamics model and flight dynamics model
飞机在地面运动状态下,起落架缓冲器由于压缩有行程和速度,形成了缓冲力,通过机轮作用到地面,地面再反作用给机轮支反力和摩擦力,从而形成起落架在体轴系的力和力矩。因此,起落架动力学模型首先需要根据飞机当前运动状态计算起落架承载情况及缓冲器压缩运动参数,然后根据因压缩形成的缓冲力解算机轮受到的支反力和摩擦力,最后将机轮受力投影到飞机体轴系上,输出体轴系上的力和力矩供运动方程解算,其结构示意图如图2所示,其中前轮偏转角度、前轮轮轴与转向轴的向量为前起落架所特有结构;最后将所有起落架在体轴系上的力和相对于重心的力矩进行叠加,得到起落架作用于飞机的力和力矩。

图2 起落架动力学模型结构Fig.2 The structure of landing gear dynamics model
为确保起落架动力学模型的准确性,需根据起落架原本结构进行建模,起落架模型结构如图3所示。
图3中,λ为前起落架前倾角,pm和pn分别为主起落架和前起落架在机体构造坐标系下压缩方向的向量,(xO,yO,zO)和(xo,yo,zo)分别为主起落架和前起落架未压缩时轮轴在机体构造系的坐标,R和r分别为主起落架和前起落架机轮的半径,ln为前起落架轮轴到压缩轴在机体构造坐标系下的向量。
2 轮载的判定
由于机轮外轮廓是圆形,机轮距离地面的最低点(或机轮触地点)与飞机的姿态相关,其在飞机构造系(以飞机鼻锥为原点,x轴沿机身轴线向后为正,y轴垂直于飞机对称平面向右为正,z轴垂直于x-y平面向上为正)下的坐标不固定,因此首先需要确定机轮最低点在构造系下的坐标,从而得到机轮轴的地面高度。
由于飞机在偏航时,起落架机轮跟随飞机进行偏航,所以起落架机轮最低点(触地点)只与飞机俯仰和滚转姿态相关(转向起落架还与转向角和转向轴前/后倾角有关)。先以主起落架为例,起落架机轮相对于地面的姿态角定义同飞机欧拉角一样,先俯仰后滚转。
2.1 主起落架
建立机轮构造坐标系,以机轮轴心为原点,x轴在机轮对称面内平行于机体构造系x-y面向后为正,z轴在机轮对称面内垂直机体构造系x-y面向上为正,y轴垂直于轮胎对称面向右为正,如图4所示。
机轮外轮廓可由极坐标方程表示为
(1)
式(1)中:下标w表示机轮构造坐标系坐标;R为主起落架机轮半径;ε为极坐标因子,为原点到轮廓任意一点与x轴的夹角。
建立机轮牵连地轴系,以机轮轮轴为原点,x轴为机轮构造坐标系x轴在地面的投影向后为正,z轴为垂直于地面向上为正,y轴垂直于x-z平面向右为正,如图5所示。
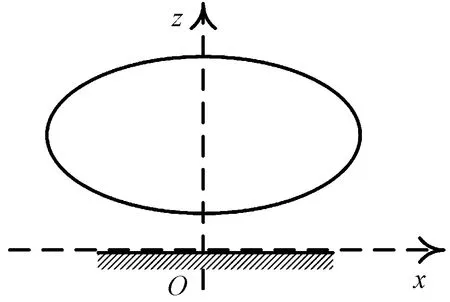
图5 机轮牵连地轴系示意图Fig.5 Schematic diagram of wheel implicated earth coordinate system
若机轮对称面和机体对称面平行,则机轮外轮廓坐标转换到机轮牵连地轴系下为
(2)
式(2)中:下标mg表示主起落架机轮牵连地轴系坐标;Lgw为机轮外轮廓坐标系到机轮牵连地轴系的转换矩阵;L′wg为机轮牵连地轴系到机轮外轮廓坐标系转换矩阵的转置。
Lwg=Lx(φ)Ly(θ)
(3)
式(3)中:Li(σ)为绕i轴旋转角σ的转换矩阵,i可以为x、y、z轴中任一个;σ可以为φ、θ中任一个,φ为滚转角;θ为俯仰角。
(4)
机轮最低点(触地点)的地轴z坐标有最小值,将z轴坐标对ε求导,可得
(5)

因此机轮最低点(触地点)在机体构造系的坐标(xm,ym,zm)为
(6)
式(6)中:(xO,yO,zO)为起落架支柱未压缩时,主起落架机轮轮轴在机体构造系的坐标。
由飞机的姿态可推出机轮最低点(触地点)在地轴系下的坐标(xmG,ymG,zmG),可表示为
(7)
式(7)中:(xg,yg,zg)为飞机重心在构造坐标系下的坐标;(xG,yG,zG)为飞机重心在地轴系下的坐标;ψ为偏航角。
如果求得zmG≥0(地轴系向下为正),则该主起落架机轮触地有轮载。
2.2 前起落架
前起落架机轮最低点(触地点)的计算与主起落架类似,不同的是前起落架机轮可偏转,而且由于前起落架有前倾角的原因,前起落架机轮偏转的旋转轴和体轴系的z轴不平行,故需先将机轮构造坐标(定义同主起落架机轮)转换到和体轴系平行,经前机轮偏转后再转换回前起落架的机轮构造坐标系。因此对于前起落架机轮,机轮外轮廓坐标转换到机轮牵连地轴系的过渡矩阵为
Lwg=Ly(-λ)Lz(δ)Ly(λ)Lx(φ)Ly(θ)
(8)
式(8)中:δ为前轮偏度(机轮左偏为正);λ为前起落架前倾角(支柱前伸为正)。

ε=arctan{(cosθcosφcosλ-sinθsinλ)cosλ+[(sinθcosλ+cosθcosφsinλ)cosδ-
cosθsinφsinδ]sinλ}{(cosθcosφcosλ-
sinθsinλ)sinλ-[(sinθcosλ+
cosθcosφsinλ)cosδ-cosθsinφsinδ]cosλ}-1
(9)
由于前起落架机轮轮轴一般不在转向轴上,所以前轮偏转时轮轴的机体构造系坐标会发生变化,令轮轴到转向轴连接处在机体构造坐标系下的向量为ln(前起落架未偏转时),则前起落架机轮最低点(触地点)在机体构造系的坐标(xn,yn,zn)为
(10)
式(10)中:(xo,yo,zo)为前起落架未转向的机轮轮轴在起落架支柱未压缩时的机体构造系坐标。
再由飞机姿态推出机轮最低点(触地点)在地轴系下的坐标(xnG,ynG,znG)可表示为
(11)
如果求得znG≥0(地轴系向下为正),则前起落架机轮触地,有轮载。
3 起落架缓冲力的计算
起落架缓冲器所提供的缓冲力是起落架提供给飞机支反力的主要组成部分,主要由随压缩行程变化的弹簧力、随压缩速率变化的阻尼力以及缓冲器内部有相对运动而产生的滑动摩擦力组成。
3.1 压缩行程
当计算得到主起落架机轮触地有轮载时,则主起落架缓冲器被压缩。令主起落架的压缩方向在机体构造系下为pm=[pmx,pmy,pmz],将其转换到地轴系下,压缩方向pmG,可表示为
(12)
由此可得主起落架压缩行程Lm为
(13)
上述计算过程对于前起落架同样适用。
3.2 压缩速率
压缩速率可通过缓冲器无压缩时(假设未触地)机轮轮轴地速和实际压缩时(实际已触地)的机轮轮轴地速在压缩方向的差求得。轮轴的地速是重心速度与绕重心转动的线速度之和。
3.2.1 无压缩时机轮轮轴沿压缩方向速度
令飞机重心的地速为Vg=[Vgx,Vgy,Vgz],则无压缩时主起落架机轮轮轴沿压缩方向的地速Vmg_uncomp可表示为
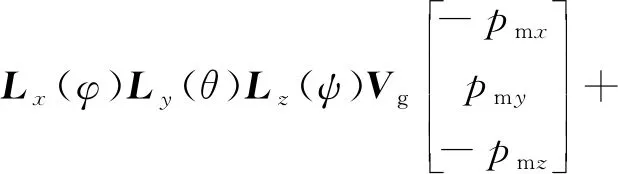
(14)

3.2.2 压缩时机轮轮轴沿压缩方向速度
压缩时机轮轮轴沿压缩方向的速度计算方法与未压缩时相似,不同点在于:①轮轴与重心在机体构造系下的相对位置有变化;②压缩时轮轴地速在机轮牵连地轴系z轴的分量为0。由此可推出主起落架压缩时机轮轮轴沿压缩方向的地速Vmg_comp可表示为

(15)
因此主起落架缓冲器的压缩速率为
Vm_comp=Vmg_uncomp-Vmg_comp
(16)
同理可计算前起落架的压缩速率,不同的是式(14)、式(15)中未压缩机轮轮轴在机体坐标系的坐标(xO,yO,zO)修正为前起落架偏转后的未压缩机轮轮轴在机体坐标系的坐标,即
(17)
3.3 缓冲力
根据起落架缓冲器的结构和参数可以得到缓冲器弹簧力、阻尼力与压缩行程、压缩速率的函数关系;滑动摩擦和压缩速率有关,即有压缩速率就有反向的固定滑动摩擦力(滑动摩擦力具有消除仿真振荡的作用,只采用弹簧-阻尼特性的缓冲器会存在振荡现象[21])。由此可得主起落架的缓冲力Fm_comp为
Fm_comp=Fm_spring(Lm)-sgn(Vm_comp)×
Fm_damp(Lm,Vm_comp)-sgn(Vm_comp)Fm_0
(18)
式(18)中:Fm_spring(Lm)为主起落架缓冲器弹簧力与压缩行程的函数关系;Fm_damp(Lm,Vm_comp)为阻尼力与压缩行程和压缩速率的函数关系;Fm_0为滑动摩擦由起落架缓冲器的设计决定,其具体形式由起落架设计方提供。同理可得前起落架的缓冲力。
4 机轮摩擦力的构成
起落架机轮和地面的受力关系除了地面提供支反力以外还有摩擦力,摩擦力根据机轮滚动的方向分为纵向摩擦力和侧向摩擦力,其中沿机轮滚动方向的摩擦分量为纵向摩擦,垂直于滚动方向的摩擦分量为侧向摩擦。
4.1 纵向摩擦
主起落架的纵向摩擦包含滚动摩擦和刹车压力摩擦,前起落架只有滚动摩擦。滚动摩擦系数根据跑道面的不同而为不同的常数,刹车压力摩擦系数是刹车压力的函数,由于刹车压力与刹车踏板偏度有近似一一对应的关系,刹车压力摩擦系数也可以认为是刹车踏板偏度的函数。由此,起落架的纵向摩擦系数为
(19)
式(19)中:μm_long为主起落架纵向摩擦系数;μn_long为前起落架纵向摩擦系数;μ0为滚动摩擦系数;μbreke(pedal)为刹车摩擦系数,其中pedal为刹车程度。
4.2 侧向摩擦
当机轮运动方向不在机轮对称平面内时,机轮存在侧向摩擦。机轮的侧向摩擦系数是机轮运动方向与机轮滚动方向夹角(即侧偏角βm)的函数,侧偏角较小时,侧向摩擦系数与侧偏角近似成线性关系。侧偏角可视为机轮运动方向和机轮地面坐标系x轴的夹角与机轮地面坐标系x轴和机轮滚动方向夹角的和。此外由于机轮存在最大摩擦系数,侧向摩擦系数应小于最大摩擦系数与纵向摩擦系数的几何差,所以主起落架机轮侧向摩擦系数的形式为
(20)
(21)
式中:μm_lat为主起落架侧向摩擦系数;μm_max为主起落架最大摩擦系数;μβ(βm)为侧向摩擦随侧偏角的函数;(Vmgx,Vmgy,Vmgz)为主起落架轮轴在地轴系的地速;δmg为主起落架机轮滚动方向与机轮牵连地轴系的夹角。
μβ(βm)有多种轮胎模型可使用,可采用魔术公式轮胎模型或Dugoff轮胎模型[22]。为求解主起落架机轮滚动方向相对于机轮地轴牵连系的偏度δmg,需明确机轮滚动方向。由于机轮在只受摩擦力的情况下,在机轮轮廓平面内滚动,因此定义一个垂直于轮轴到触地点向量并在机轮对称平面内的单位向量,其机轮构造坐标系的坐标为[-sinε,0,cosε],该单位向量在机轮牵连地轴系的投影与机轮牵连地轴系x轴的夹角即为δmg,可表示为
(22)
式(22)中:(δmgx,δmgy,δmgz)为主起落架单位向量在机轮牵连地轴系的方向。
前起落架机轮侧向摩擦系数与主起落架相似,但由于前起落架可偏转的原因,式(23)中未压缩机轮轮轴在机体坐标系的坐标修正为前起落架偏转后的未压缩机轮轮轴在机体坐标系的坐标为
(23)
式(23)中:βn为前起落架机轮的侧偏角;(Vngx,Vngy,Vngz)为前起落架轮轴在地轴系的地速;δng为前起落架机轮滚动方向与机轮牵连地轴系的夹角;Ln为前起落架的压缩行程。
前起落架机轮滚动方向相对于机轮地面坐标系偏度的计算中,也要考虑前起落架前倾角和转弯偏度的因素,可表示为
(24)
式(24)中:(δngx,δngy,δngz)为前起落架单位向量在机轮牵连地轴系的方向。
5 支反力的求解
对于机轮触地点,地面对于机轮的支反摩擦力和机轮施加于地面的压力是一对大小相等、方向相反的力。根据上述章节已求出缓冲力和地面各摩擦力的系数,其中缓冲力只是这对力在缓冲器压缩方向的分力,垂直于压缩方向还存在应力;地面各摩擦系数和地面压力的关系可确定合力的方向,因此已知分力大小和合力方向,可求解出合力的大小和方向,以主起落架为例,合力大小Fm为
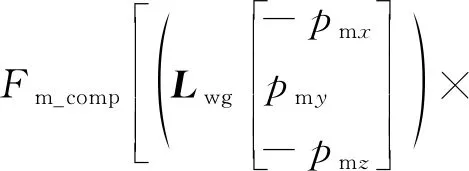
(25)
建立机轮地面坐标系,以机轮触地点为原点,x轴为轮轴滚动方向向前为正,y轴为轮轴在地面的投影向右为正,z轴为垂直于地面向下为正,如图6所示。可得到合力在主起落架机轮地面坐标系的各分力Fmg为

图6 机轮地面坐标系示意图Fig.6 Wheel earth coordinate sytem
(26)
前起落架机轮由于有转向,式(25)中Lwg的形式[式(8)]与主起落架有区别。
6 起落架相对机体的力和力矩
将机轮地面坐标系的分力转换到体轴系上,可得主起落架对机体的力FGear_m为
FGear_m=Lx(φ)Ly(θ)Fmg
(27)
前起落架有同样的形式。
主起落架对机体的力矩MGear_m由主起落架对机体的力叉乘机轮相对重心在体轴系的坐标可得
(28)
起落架的力矩计算需要将式中未压缩机轮轮轴在机体坐标系的坐标(xo,yo,zo)修正为前起落架偏转后的未压缩机轮轮轴在机体坐标系的坐标,如式(17)所示。
将所有起落架的力和力矩相加就得到起落架系统对飞机在体轴系上的力FGear和力矩MGear为
(29)
7 仿真验证
起落架动力学模型主要实现飞机在地面的落震、转弯、刹车功能,为验证该起落架动力学模型的正确性,对以上3个功能进行仿真验证。同时为了适用于有运动平台的飞行模拟器,确保着陆时的过载与实际相符,对着陆工况进行仿真验证。
7.1 落震
设置飞机初始高度稍高于地面,俯仰角为3°,呈稍抬头的姿态,确保主起落架先触地;速度为0.5 m/s,避免迎角侧滑角解算出现奇点。落震过程重心高度和俯仰角变化曲线如图7所示。
由图7可见,飞机在落震过程中,重心高度经过三次振荡后稳定(由于起落架有高度,静止后飞机重心高度为正值),并且由于抬头的初始姿态,飞机初始有俯仰的振荡,最终快速收敛稳定。这与实际试验现象相符[23]。
7.2 转弯
设置飞机在第10秒左蹬脚蹬,第14秒时收回,偏航角、滚转角、前起落架机轮侧偏角及3个起落架机轮的轨迹如图8所示。

机轮轨迹是由空中向地面俯瞰图8 转弯过程中仿真结果Fig.8 Simulation result of turning process
由图8可以看到,左蹬脚蹬后飞机航向向左偏转,脚蹬回中后航向保持在松脚蹬的时刻;转弯过程中,飞机由于向右的离心力会产生轻微的右滚转;前机轮偏转后,机轮速度方向很快靠近滚动方向。
7.3 刹车
设置初始速度为40 m/s,第5 s开始持续满刹车,速度、俯仰角变化如图9所示,开始刹车后飞机低头、速度急速减小;因为机轮位于重心以下,刹车带来低头力矩。

图9 刹车过程的仿真结果Fig.9 Simulation result of breaking process
7.4 着陆
设置初始速度为着陆速度,飞机略高于地面并以抬头姿态进行着陆。着陆时重心高度、俯仰角及重心法向过载如图10所示,着陆触地后,重心高度和俯仰角经过一次振荡就快速收敛。由于仿真初始设置为“硬着陆”,所以最大法向过载约3.5g(g为重力加速度),该过载值允许飞行模拟器带上运动平台给飞行员提供着陆触地时的过载感受。

图10 着陆过程的仿真结果Fig.10 Simulation result of landing process
8 结论
(1)在没有忽略起落架结构尺寸和受力方式的基础上建立了受力特性完整的起落架动力学模型。
(2)由仿真结果可知,飞机落震经过3次缓冲振荡后收敛稳定;飞机的航向跟随前机轮的偏转而改变,前机轮回中后保持回中时刻的航向,转弯过程中向转弯相反的方向倾斜;刹车时飞机速度快速较小并产生低头的姿态。
(3)着陆仿真的过载仿真允许将该模型加载到带运动平台的飞行模拟器中,使飞行模拟器可模拟任意状态下的地面运动并提供给飞行员真实的起降滑跑体验。
