气井积液理论预测及室内实验验证

牛 骏， 柯文奇

(中国石油化工股份有限公司石油勘探开发研究院， 北京 100083)

天然气开采井中常遇到流向反转现象，从而引发“气井积液”，积液的气井产量会显著减小，甚至提前停产[1-2]，因此需要采取一定缓解措施对井筒进行排液。目前常用的排液手段包括泡沫排液、气举排液、井下雾化器等[3]。为了更好地应用排液措施，需要知道在何时进行排水采气作业，即预测气井在何时发生“气井积液”。 此外，有学者通过现场井筒数据拟合得到临界携液流量的预测模型为后续研究提供了经验参考[4]。准确预测气井积液需要深入研究积液的机理，分析导致气井积液的原因，建立合理的积液预测模型。

液滴流动反转和液膜流动反转理论是解释气井积液机理的两种主要观点，液滴反转理论认为井筒内气速降低后，液滴在重力作用下向下流动反转，进而引发积液现象；液膜反转理论认为液体主要以液膜的形式存在于管壁，当气速较高时，气体携带液膜向上流动，当气体流速降低时，气液两相之间的剪力不足以携带液膜流动，液膜在重力作用下开始反转，从而导致积液，目前使用最广泛的液膜反转模型为Barnea[5]提出的理论。虽然液膜反转模型较复杂，但是更符合气液两相环状流动的实验现象。此外，由于积液是产量骤降的瞬态行为，近年来一些研究者也从井筒-储层耦合的角度对积液现象进行解释和分析，目前处于理论研究阶段，尚无能够推广应用的计算模型。

为此，从积液机理出发进行研究，建立理论模型，计算临界携液流量，对气井积液实现理论预测。通过室内实验模拟井筒中低气速下两相流动，测量液滴尺寸并观测分析液膜流动现象，进一步验证预测模型的有效性，并结合多井现场数据验证模型的普适性。

1 理论预测模型的建立

在现场作业中，基于液滴反转理论建立的积液预测模型已得到了广泛应用，但是一直缺乏系统的理论预测和实验证明。近年来，一些学者通过室内实验发现液膜在低气速下反转才是引发积液的原因，特别在倾斜井中，液膜反转模型的准确性更高，更能反映气液两相流动行为[2]，在液膜反转机理的基础上进行理论模型的建立。

1.1 液膜反转准则分析

液膜反转预测点的判断准则有两种方式：最小气液界面剪力和零壁面剪力，两种判断准则分别由液膜流动稳定性分析和层流速度假设得出，而两种判断方式得到的临界气速存在一定差异，因此有必要在模型建立前对液膜反转的判断准则进行分析。

1.1.1 稳定性分析

Barnea[5]提出的液膜反转模型本质是环状流到搅拌流的过渡，根据无量纲液膜厚度和气液界面剪力关系，可以对液膜的稳定性进行分析。

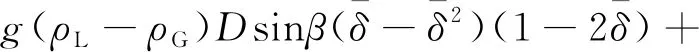
(1)

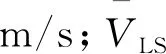
图1 无量纲界面剪力和无量纲液膜厚度关系Fig.1 The relationship between non-dimensional interface shear and non-dimensional liquid film thickness

根据分析可以得出，液相曲线的最小值为液膜稳定流动的临界点，该点对应的气相速度即为液膜反转临界速度。

1.1.2 零壁面剪力

一部分研究者认为，液膜在环状流中的流动为层流状态，当气体流速不足以携带液膜连续向上流动时，壁面附近的液膜速度会降低为零，此时对应的壁面剪力也为零，该方法可以通过N-S方程或者哈根-泊肃叶方程导出。

使用牛顿内摩擦定律和力的平衡对液膜进行分析。假设环状流状态下，附着在管壁的液膜厚度足够小，根据牛顿内摩擦定律和力的平衡，可以得到剪力和液膜速度梯度的关系。

(2)

式(2)中：τ为剪力，Pa；μL为液体动力黏度，Pa·s；y为与壁面的径向距离，m；P为压力，Pa；z为轴向距离，m；δ为液膜厚度，m。

对式(2)进行积分，得到速度V表达式为

(3)

在液膜厚度上对式(3)积分，得到液相表观流速的表达式为

(4)

对气相进行力学平衡分析，得到关系式为

(5)

将式(5)代入式(4)，得到界面剪力和液相表观流速、液膜厚度关系式为

(6)

将其无量纲化，得到关系式为

(7)

(8)

(9)

(10)

(11)

对界面剪力和液膜厚度关系求导，得到最小界面剪力准则对应的临界液膜厚度计算公式为

(12)

若壁面剪力等于零，可将式(2)改写为

(13)

结合式(4)和式(5)，可得到零壁面剪力准则对应的临界液膜厚度为

(14)

1.2 液膜反转模型建立

由最小界面间剪力准则得到液膜反转临界厚度和临界界面剪力后，结合气相的流动模型，可以导出液膜反转的临界表观气体流速。

气相流动提供的气液界面间剪力为

(15)

式(15)中：fi为界面摩擦系数，将式(15)无量纲化，可以得到无量纲临界表观气速表达式为

(16)

式(16)为计算携液临界流速的基本公式，将式(14)和式(7)得到的临界气液界面剪力和临界液膜厚度代入式(16)，即可得到临界携液气体流速。需要注意的是，准确预测临界流速还需要合理考虑倾斜角对液膜厚度的影响以及界面间摩擦系数。模型采用Belforid等[6]提出的经验关系引入倾斜角对临界携液流速的影响，用参数K表示为

(17)

与前人研究不同，根据实验数据拟合提出新的界面摩擦系数式(17)，考虑本文模型针对液膜流动计算，仍保持Wallis[7]摩擦系数形式，修正后的摩擦系数表达式为

(18)

综上，可得到临界携液表观气速表达式为

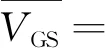
(19)

与室内实验条件不同，井筒中流体介质一般为高温高压条件下的天然气和水，其中天然气属于可压缩气体，因此需要根据非理想气体状态方程换算得到实际井筒内的天然气物性参数，再计算临界携液流量。根据天然气井工况，临界产量的表达式为

(20)

式(20)中：q为井口产量，m3/D；A为油管横截面积，m2；P为气体压力；VG为气体流速；Z为天然气压缩因子；T为环境温度，K。

2 模型分析

2.1 液体流速与液膜厚度的关系

根据式(12)、式(14)，不同液体流量下的临界液膜厚度曲线如图2所示，在同一液体流速下，零壁面剪力准则得到的临界液膜厚度大于最小界面剪力准则得到的液膜厚度，表明随着气体流速减小，液膜先达到不稳定点，再达到零壁面剪力点。考虑到液膜在达到不稳定点以后难以维持液膜形态，零壁面剪力点不一定会在物理条件下出现，因此本研究认为最小界面剪力准则决定了液膜反转的临界工况。

图2 液体流速与临界液膜厚度关系Fig.2 The relationship between liquid flow rate and critical liquid film thickness

2.2 临界携液气体流速与气液界面剪力的关系

垂直管道中，气体运动提供的气液界面剪力与气相速度密切相关，临界携液表观气相速度与气液临界界面剪力的关系如图3所示。

图3 气体速度与临界界面剪力的关系Fig.3 The relationship between gas velocity and critical interface shear

分析表明，随着界面剪力的增大，临界携液气体流速呈现增大的趋势，在界面剪力为8 Pa附近时，携液表观气相速度增至最大，此时临界携液气相流速值为管道内形成稳定液膜时对应的气体速度。随后随着界面剪力的进一步增加，临界携液气相速度变化不明显，甚至稍有下降，其原因是通过增大液相表观速度进一步增加相间界面剪力，将导致液膜稍有变厚，相间摩阻增大能量损失稍有增加，表现为携液表观气相速度有所减小。

2.3 临界表观携液气相速度与倾斜角度的关系

针对所提出的临界携液表观气相速度预测模型，进一步分析可得到临界携液表观气相速度随管道倾斜角度变化情况。由图4可知，设定管道垂直位置为倾斜角度90°，随着管道倾斜角度的减小，临界携液气相表观速度呈现先增加后减小的趋势。分析可知，在管道倾斜角度为50°～60°时，气相速度达到最大值，随后管道继续倾斜，临界携液气速逐渐减小，这一规律存在于不同液体流速下，并且与文献[8-9]调研结果一致，也进一步验证了本文提出的新模型的有效性。

图4 气体速度与管道倾斜角度的关系Fig.4 The relationship between gas velocity and pipe inclination angle

2.4 不同压力下临界产量的变化预测

由预测模型可知，压力的变化将直接影响井口产量，如图5所示。随着井口压力的增加，临界产量呈现增长的趋势，但增长速度有所减缓，直至临界产量趋于稳定。进一步分析表明，相同井口压力下，临界携液产量随着液气比的增大逐渐减小，这一规律在较大井口压力(大于14 MPa)时较为显著，而在井口压力较小时表现不明显。

图5 井口压力与临界携液产量的关系Fig.5 The relationship between wellhead pressure and critical liquid-carrying production

3 理论预测模型验证与评价

3.1 实验数据验证

开展24组气井积液室内模拟实验，模拟管道中气液两相流动现象，重现液体反转行为，通过实验观察和参数测量对气井积液机理进行研究，进而验证本文提出的理论预测模型的有效性。

实验工作在中科院力学研究所的多相流实验平台完成。该平台可实现气-液、液-液两相管流的实验模拟。积液模拟实验流程如图6所示。测试管为高3.2 m、直径50 mm的透明有机玻璃管道。液体通过管道下部的进液口注入，气体通过管道底部进入。当气流速度足够大时，气体携带液体向上流动。在流动发展段对实验参数进行观察和测量。在高度为2.5 m处通过去液膜装置剥离回收管道上部的液膜，测量液膜流量。剥离液膜后可测定气芯中夹带的液滴尺寸。

图6 实验流程图Fig.6 Experimental flowchart

实验表观液体流速设置为0.014、0.028、0.042、0.071 m/s，表观气体流速为22.64、19.81、16.98、14.15、11.32、8.49 m/s，实验工况的气液比范围1 600～120，测量参数包括流动现象摄像记录、液滴粒径以及液膜流动速度。

3.1.1 液膜反转机理验证

实验进行了5个不同气液比工况下的液滴粒径在线测量，测量结果显示，液滴尺寸随着气液比的降低而减小，但范围波动不大。最大液滴尺寸分布出现在气液比为1 463∶1时，该工况下累计体积分数90%的液滴尺寸为1 863.87 μm，图7显示当气液比为1 463∶1时，2 500 μm的液滴尺寸占比陡增为22%，这可能是因为在大气量工况下，液滴在取样管中出现了聚并行为，聚并后的液滴尺寸为2 500 μm，考虑到该次测试可能出现液滴聚并现象，实际的液滴尺寸会更小，且最大液滴尺寸不超过2 500 μm。累计体积分数50%的液滴尺寸范围为50～192 μm，累计体积分数10%的液滴尺寸范围为7.56～30.50 μm，结果表明大多数液滴尺寸较小，在液体反转工况下，液滴尺寸最大不超过2 500 μm。

图7 液滴尺寸分布Fig.7 Droplet size distribution

Turner等[10]提出的液滴反转模型计算得到最大液滴尺寸范围为3 201～9 024 μm，远大于研究实测的液滴尺寸(2 500 μm)，表明液滴反转不是形成气井积液的主导因素。由此可见，选用的液膜反转机理是合理的，得到了实验数据的佐证。

3.1.2 临界携液表观气速预测模型验证

采用高速摄像机记录不同工况下液膜流动情况，通过图像分析确定液膜出现回落的气体流动速度范围，实验摄像记录如图8所示。结果表明，当气体流速为22.64 m/s时，所有液体流速下的液膜都处于连续向上流动状态，此时液膜上的波纹较少，随着气体流速的降低，液膜变厚，界面波变得显著，液膜中夹带的气泡增加。当气体流速降低至16.98 m/s时，界面波变得显著，视频记录显示液膜开始上下震荡，表明此时液膜有回落趋势。虽然此时液体出现回落，但是液膜向下移动一段距离后很快继续向上流动，因此液膜处于反复上升-反转的流动状态。进一步减小气速为11.32 m/s和8.49 m/s，液膜厚度显著增加，甚至在大液量工况下(表观液速0.071 m/s)不能维持液膜形态，液体以块状的形式在管道中上下反复运动，表明流型逐渐向段塞流过渡，当气体流速降低至8.49 m/s以下时，段塞流出现。

图8 表观液速为0.028 m/s的图像记录Fig.8 Image recording at the superficial liquid velocity is 0.028 m/s

将液膜反转范围限定在气体流速为16.98～14.15 m/s，根据分析液膜流动轨迹和高速摄像，确定液膜流动反转临界气体流速。本文模型和室内模拟实验结果对比如表1所示，相对误差最大为8.73%，最小为6.38%，误差均不超过10%，表明新模型的准确度较高。

表1 实验值和预测值比较Table 1 Comparison of experimental and predicted values

使用已发表文献的110组室内实验数据和液膜反转模型比较，数据取自Guner等[9]、Alsaadi等[11]、Fan等[12]、Liu等[13]、Skopich等[14]、Rastogi等[15]、Vieira等[16-17]，涵盖的管道尺寸范围为30～152 mm，倾斜1°～90°，流体介质包括空气-水和空气-油。对比结果如图9所示，与前人模型相比，新模型和110组已发表实验的结果吻合效果最好，相对误差仅为11.62%。此外Shekhar模型和Liu模型的相对误差也较低，分别为11.81%和15.16%。3个模型的详细对比如图10所示，当倾斜角为90°(垂直管)～10°时，新模型的误差小于Shekhar模型和Liu模型，这表明在垂直井和定向井预测中，新模型的准确度更高。而当倾斜角小于10°时，3个模型的相对误差相近，特别当倾斜角小于10°时，相对误差都显著变大，因此目前的液膜反转模型对水平管的临界流速预测准确度还有待改进。但前人研究实验研究已经表明，积液气井的最大临界流速发生在倾斜角为60°左右，所以目前新模型满足一般气井的工程应用，可以用来预测气井携液临界流速。

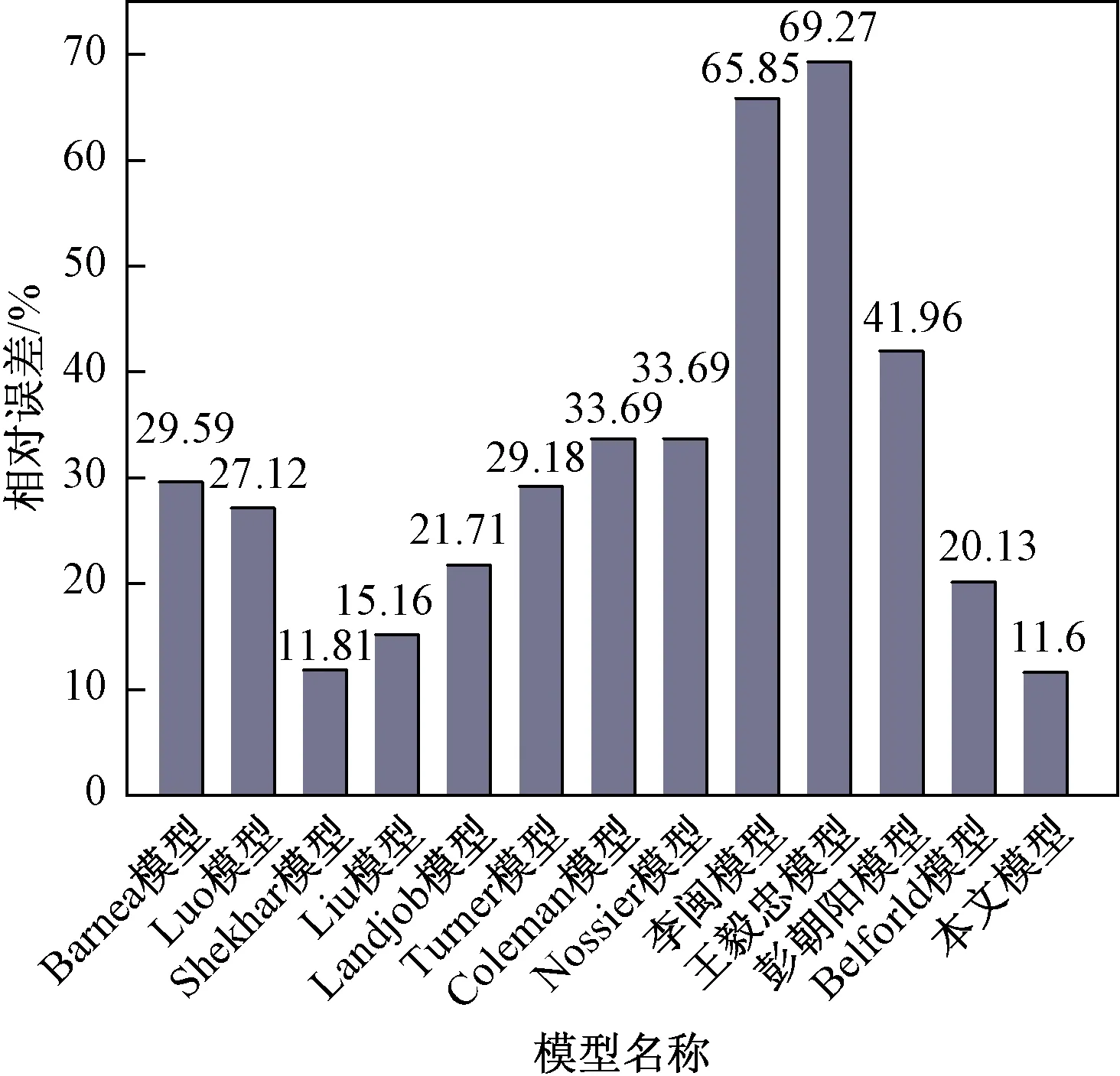
图9 各模型相对误差Fig.9 The relative error of different models

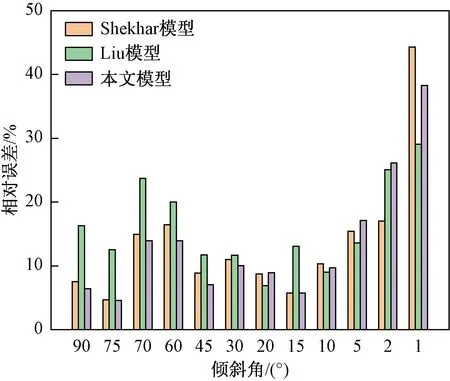
图10 不同倾斜角下不同模型的相对误差Fig.10 The relative error of different models under different tilt angles

3.2 现场数据验证

使用公开发表的气井数据对模型进行验证计算，收集了文献[10-17]中的气井数据共191口，其中积液井136口，未积液井55口。由于Barnea模型在积液预测中应用广泛，Shekhar模型在分析中准确度较高，将本文模型与Barnea模型、Shekhar模型进行比较。对比情况如图11所示，结果表明，液膜反转模型准确度：本文模型>Shekhar模型>Barnea模型。在191口气井中，新模型正确预测161口，Shekhar模型正确预测158口，Barnea模型正确预测150口。因此本文模型具有更高的精度，适用于垂直井和倾斜气井中临界携液流量的预测，有助于气井施工设计，预防气井积液的损害。

4 结论

(1)根据实验测定结果得到的最大液滴粒径尺寸证实了液膜反转是气井积液的主导因素，通过建立液膜反转模型预测气井积液情况是合理的。进一步对液膜流动进行实验分析，获得了液膜流动和反转的行为特征、压力波动规律和相含率分布，基于实验现象确定了液膜反转临界流速，结果表明液膜在气体流速低于17 m/s时出现了反转行为；研究发现液膜在低气体流速下厚度增加，界面波振荡加剧，流动随气体流量降低逐渐变得不稳定，压降出现极小值，流型逐渐向段塞流过渡。

(2)通过对液膜建模分析，结果表明使用最小界面剪力准则作为液膜反转临界点更合理，进而获得液膜反转临界厚度和界面剪力。基于牛顿内摩擦定律和力学平衡建立了临界携液新模型，该模型考虑倾斜角对液膜厚度的影响，修正得到了新的界面摩擦系数。将预测模型与实验和现场数据对照，结果表明本模型的预测精度较高，可用于气井临界产量的预测。提出的修正模型有助于现场作业人员对气井进行施工设计，提前预判气井积液风险，制定合理的排水采气措施，实现天然气采收降本增效的目标。