短线法节段预制桥梁几何线形控制的坐标变换方法研究

时学军

(中铁第四勘察设计院集团有限公司,武汉 430063)

1 概述

随着桥梁施工技术的发展，短线法桥梁节段预制拼装施工具有预制用地少、自动化程度高、运输方便、工期短等优点，在桥梁建设中的应用越来越广泛[1-4]。在基于短线法的桥梁节段预制施工过程中，需根据设计线形控制每个节段在匹配位置的空间位置和姿态，从而保证拼装后的线形满足设计和施工要求[5-6]。然而，在节段预制施工过程中，受到测量误差、模板误差、温度变化等多种因素综合影响，节段的实际位置与理论位置不可避免地存在偏差[7-9]。由于节段预制完成后线形将不可调，因此，高精度几何线形控制是短线法节段预制桥梁施工过程中的一项重要工作[10-12]。

在短线法节段预制桥梁几何线形控制过程中，通过测量浇筑在节段上的控制点坐标来计算节段从浇筑位置移动到匹配位置的几何变换关系，然后评定节段在匹配位置与理论设计位置的偏差，进而对下一节段进行相应的修正，控制误差的累积，保持线形的准确性[13-14]。由此可知，控制点坐标准确的空间变化方法尤为重要，是节段预制几何线形控制的关键因素[15]。侍刚和周凌宇等[16-17]在节段预制过程中利用6个转换参数(3个平移参数、3个旋转参数)实现2个坐标系间的空间转换，忽略了尺度参数。黄跃等[18]考虑了尺度参数，利用基于7参数的Bursa模型[19]进行节段坐标变换，然而Bursa模型是一个近似的简化线性模型，只适用于微小旋转角的坐标系变换[20]，不适用于角度较大的曲线型桥梁。

从节段不同阶段间坐标空间变换的原理出发，同时考虑3个平移参数、3个旋转参数和1个尺度参数，详细推导非线性最小二乘平差计算转换参数的方法，该转换方法适用于任意旋转角度间的坐标转换。同时，将该方法在郑许市域铁路许昌段项目中进行实际应用，验证该方法的有效性。

2 几何线形控制方法

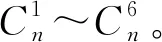
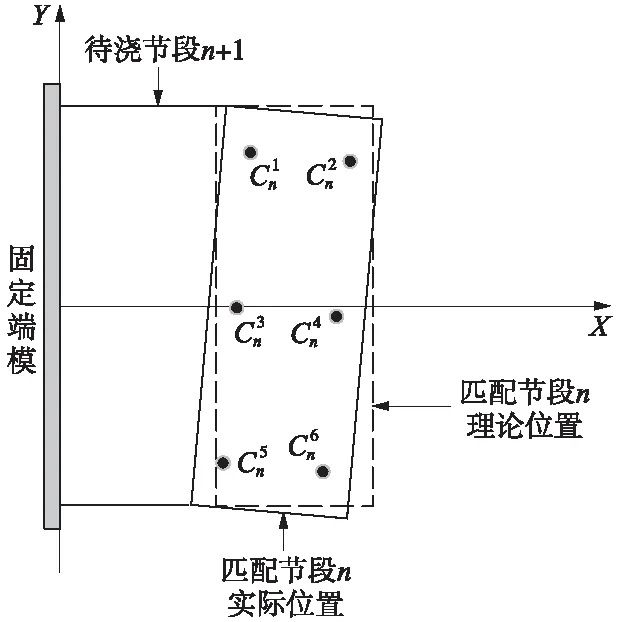
图1 短线法节段预制平面示意

将已浇筑好的节段n移动到其理论设计位置时，由于受到测量误差、人工操作、温度等各种因素综合影响，节段n无法精确移动到理论位置，不可避免地存在偏差。为保证桥梁整体线形符合设计要求，需对节段n进行误差分析，然后对待浇节段n+1进行纠偏处理，防止误差累积，短线法几何线形控制流程如图2所示。

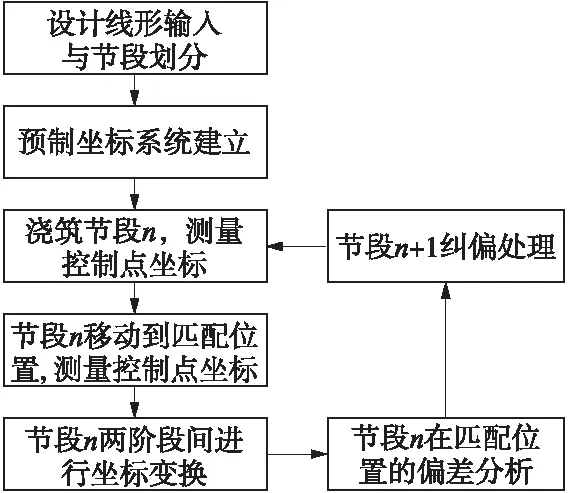
图2 短线法几何线形控制流程

3 空间坐标变换方法

3.1 空间坐标转换模型

短线法桥梁节段预制过程中关键是控制点坐标的空间变换，是进行后续误差分析与纠偏处理的基础。对空间坐标变换采用7参数模型：3个平移参数(ΔX，ΔY，ΔZ)、3个旋转参数(εx，εy，εz)和1个尺度参数K。ΔX，ΔY，ΔZ分别为X，Y，Z方向上的平移量，εx，εy，εz分别为绕X，Y，Z轴的旋转角度。由于节段从浇筑位置移动到匹配位置后，受到混凝土硬化与温度等因素影响，节段尺寸也会发生微小的变化，因此，尺度参数K也纳入坐标变换模型。基于7参数的空间坐标转换模型如式(1)所示

(1)

式中，(X1，Y1，Z1)为节段在浇筑位置时控制点的坐标；(X2，Y2，Z2)为节段移动到匹配位置后对应的控制点坐标；R(ε)为旋转矩阵。R(ε)的构建过程如下：首先将坐标轴绕X轴逆时针旋转εx，构建旋转矩阵R(εx)；再将坐标轴绕新的Y轴逆时针旋转εy，构建旋转矩阵R(εy)；最后将坐标轴绕新的Z轴逆时针旋转εz，构建旋转矩阵R(εz)。3次旋转变换合并得到旋转矩阵R(ε)

R(ε)=R(εz)R(εy)R(εx)

(2)

其中

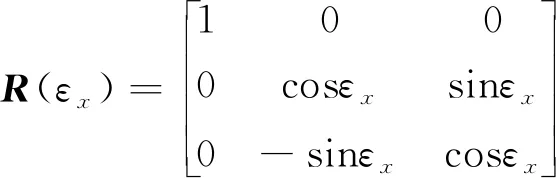
(3)

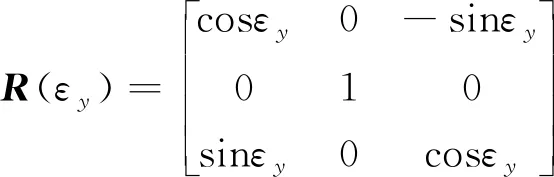
(4)

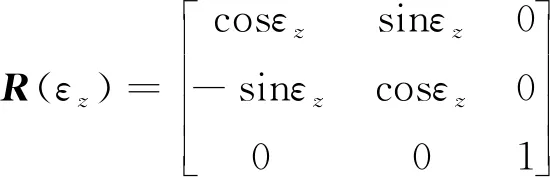
(5)

因此

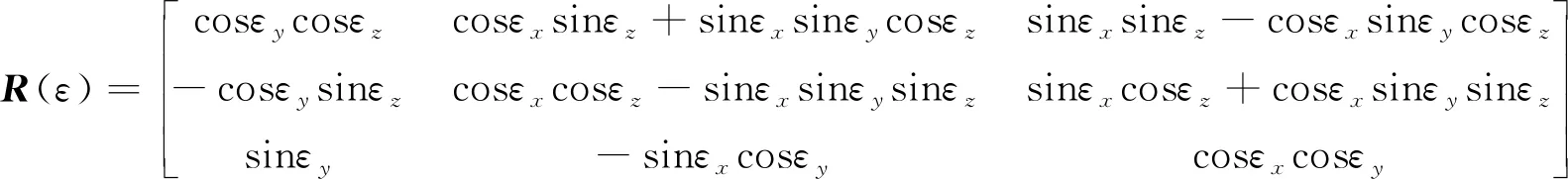
(6)

显然，式(6)代入式(1)是一个非线性方程，对于Bursa模型，认为εx，εy，εz的值很小，利用sinεx≈εx，sinεy≈εy，sinεz≈εz，cosεx≈1，cosεy≈1，cosεz≈1，sinεxsinεy≈0，sinεxsinεz≈0，sinεysinεz≈0进行近似替代，所以式(6)可以简化为

(7)

Bursa模型将简化后的旋转矩阵R(ε)代入式(1)则转换为线性方程，方便利用最小二乘进行间接平差求解计算转换7参数。

3.2 非线性最小二乘法平差

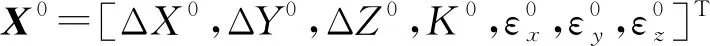
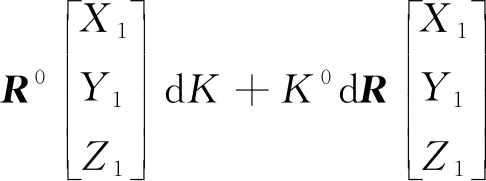
(8)

式中，dX，dY，dZ为平移参数的改正数；dK为尺度参数的改正数；dεx，dεy，dεz为旋转参数的改正数，dR为旋转矩阵的微分，其中

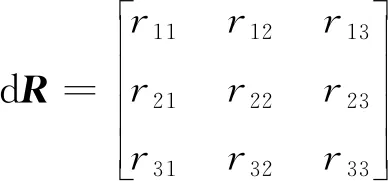
(9)

r11=-sinεycosεzdεy-cosεysinεzdεz

(10)

r12=(-sinεxsinεz+cosεxsinεycosεz)dεx+

sinεxcosεycosεzdεy+

(cosεxcosεz-sinεxsinεysinεz)dεz

(11)

r13=(cosεxsinεz+sinεxsinεycosεz)dεx-

cosεxcosεycosεzdεy+

(sinεxcosεz+cosεxsinεysinεz)dεz

(12)

r21=sinεysinεzdεy-cosεycosεzdεz

(13)

r22=-(sinεxcosεz+cosεxsinεysinεz)dεx-

sinεxcosεysinεzdεy-

(cosεxsinεz+sinεxsinεycosεz)dεz

(14)

r23=(cosεxcosεz-sinεxsinεysinεz)dεx+

cosεxcosεysinεzdεy-

(sinεxsinεz-cosεxsinεycosεz)dεz

(15)

r31=cosεydεy

(16)

r32=-cosεxcosεydεx+sinεxsinεydεy

(17)

r33=-sinεxcosεydεx-cosεxsinεydεy

(18)

式(8)依据间接平差方法可列误差方程如下

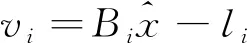
(19)

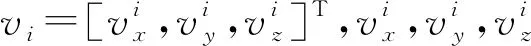
(20)

其中

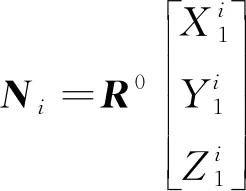
(21)

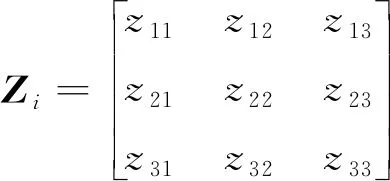
(22)

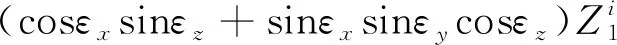
(23)

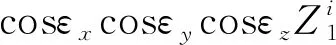
(24)

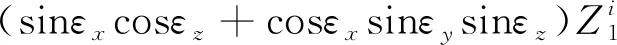
(25)

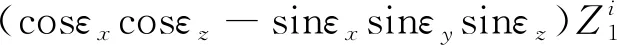
(26)

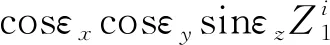
(27)

(28)

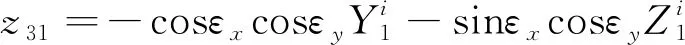
(29)

(30)

z33=0

(31)

在式(19)中，li为自由项矩阵，表示为

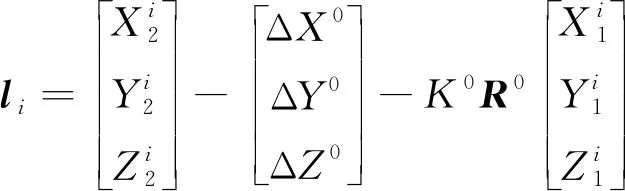
(32)

间接法平差得到参数改正数结果

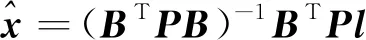
(33)

式中，P为权系数矩阵，默认P=E，另外有

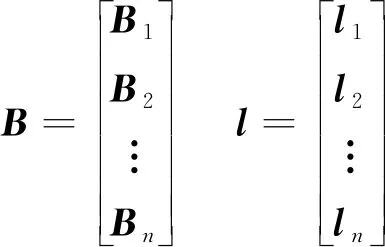
(34)

3.3 转换参数计算过程

利用最小二乘法直接平差计算得到7参数X=[ΔX，ΔY，ΔZ，K，εx，εy，εz]T的步骤如下：

(1)给定参数初值X0=[0，0，0，1，0，0，0]T；

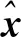
(5)计算各控制点的转换残差，判断是否有粗差点，如果有粗差点则剔除粗差点后返回步骤(1)重新迭代计算转换参数。

平差得到转换参数值后根据转换参数计算匹配节段实际位置与理论位置的偏差，然后根据设计线形对下一节段进行纠偏处理，坐标转换计算流程如图3所示。

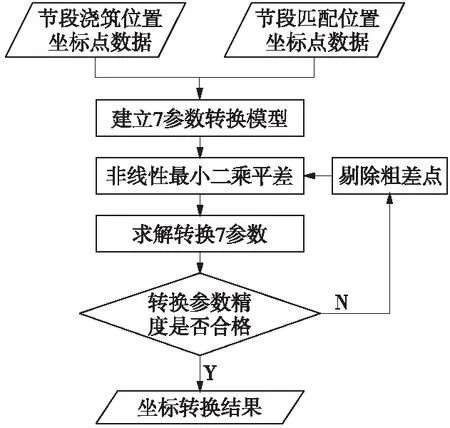
图3 坐标转换计算流程

4 工程应用实例

郑许市域铁路许昌段与郑州机场至许昌市域铁路工程郑州段接轨，线路总长33.78 km，其中，地上线长29.76 km，地下线长4.02 km，线路最小曲线半径800 m。该段线路桥梁采用后张法预应力混凝土双线简支箱梁，采用节段预制拼装法施工。简支箱梁分为12个节段进行拼接，首尾节段长度2.45 m，中间10个节段每段长度2.5 m。为进行自动化测量、数据分析计算、线形调整等工作，开发了基于安卓手机的应用程序，如图4所示。每个节段上布设6个控制点，测量操作通过手机蓝牙连接徕卡TS60全站仪进行测量。

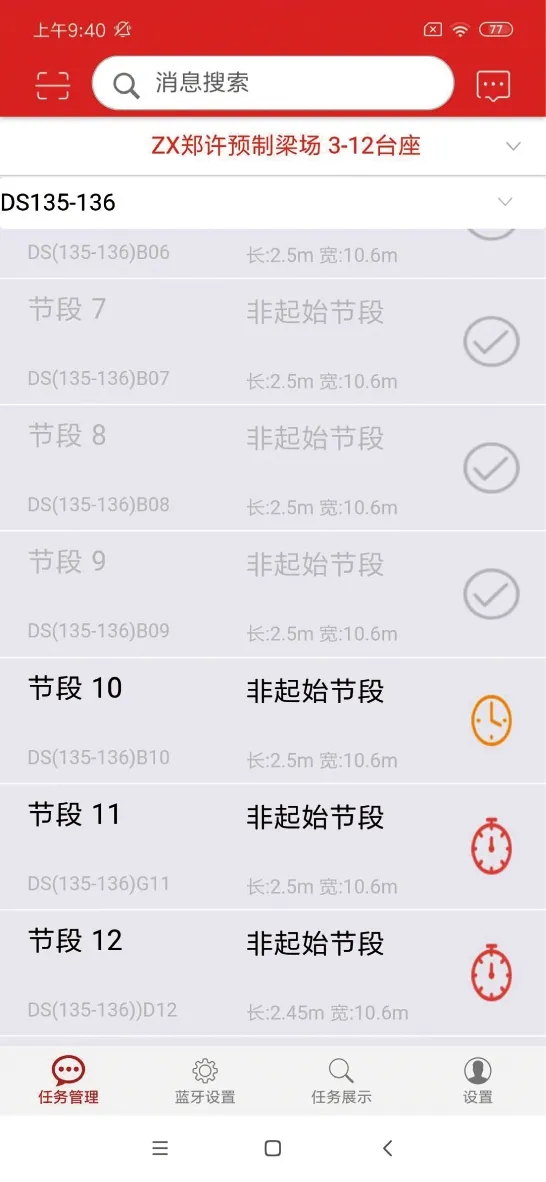
图4 手机控制程序界面

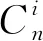
(35)

利用均方根误差RMSE(Root Mean Square Error)，来评定坐标转换算法的精度，节段n的RMSE值计算方式如下

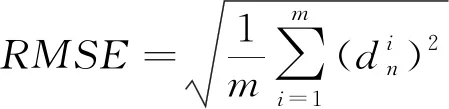
(36)

式中，m为节段上控制点数量，本文m=6。对于郑许市域铁路许昌段某一直线桥梁，计算各节段RMSE值，将该方法与Bursa模型方法对比结果见表1。

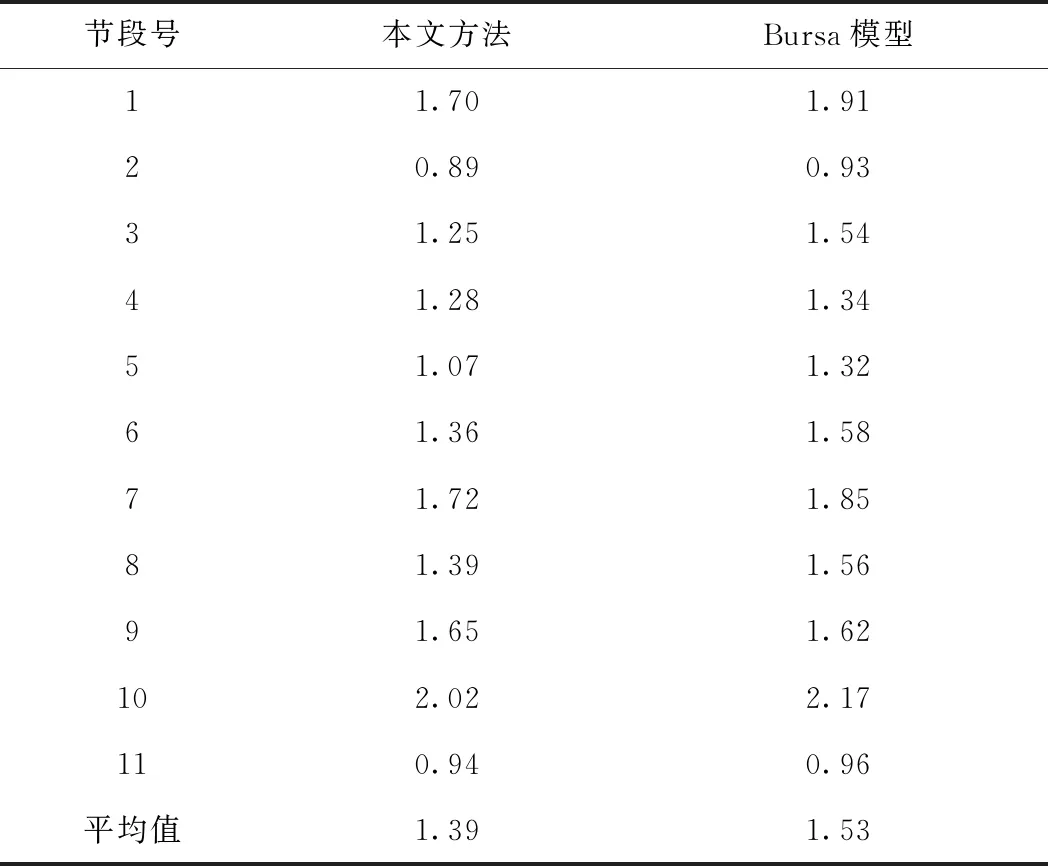
表1 直线桥梁各节段RMSE mm

从表1可以看出，在直线段桥梁上，利用本文转换算法各节段RMSE值均小于Bursa模型方法。该算法的节段RMSE平均值为1.39 mm，比Bursa模型小0.14 mm，精度提高了9%。对于某一曲线桥梁，同样计算各节段RMSE值，将该方法与Bursa模型方法对比结果见表2。

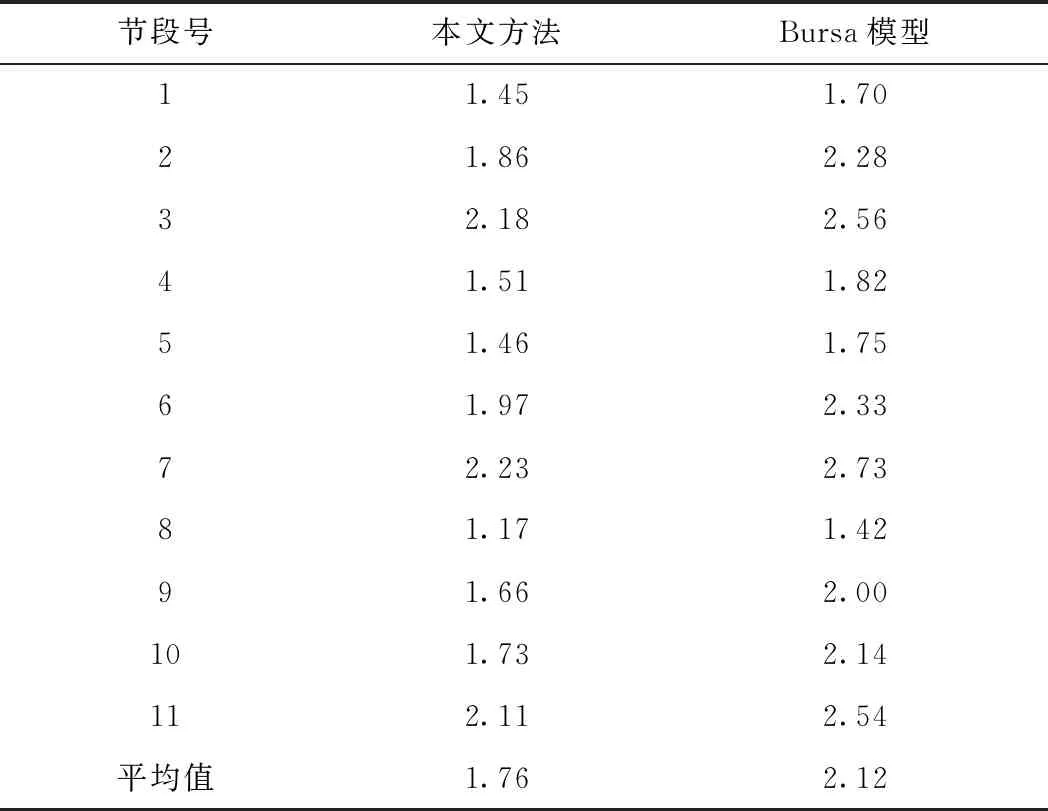
表2 曲线桥梁各节段RMSE mm

从表2可以看出，在曲线段桥梁上，本算法的节段RMSE平均值为1.76 mm，Bursa模型方法平均值RMSE为2.12 mm，本算法平均RMSE减少0.36 mm，精度提高17%，提升效果明显。本算法在曲线段上精度明显高于Bursa模型算法，主要是由于曲线桥梁上节段从浇筑位置移动到匹配位置后的偏转角度略大于直线桥梁，Bursa模型对小偏转角的计算进行了简化，而本算法采用严密的转换处理，因此在曲线段桥梁节段预制过程中坐标转换方法精度更高。

5 结语

常规基于Bursa模型的坐标转换算法只适用于微小旋转角的坐标转换，在短线法节段预制桥梁的几何线形控制过程中对于曲线形桥梁的坐标转换处理存在较大的误差。通过构建7参数坐标转换模型，详细推导了基于非线性最小二乘平差的参数求解过程，该方法适用于任意旋转角度的坐标变换，能够准确地对节段进行坐标变换，为节段误差分析和纠偏处理奠定了基础。该方法已经成功应用于郑许市域铁路许昌段的几何线形控制项目中，结果表明：该方法在短线法节段预制桥梁几何线形控制的坐标变换中具有高精度、高可靠性优势，适用于各种线形类型的桥梁线形控制，尤其在曲线段桥梁上具有更高的转换精度，能够满足实际生产过程中线形控制的精度要求。