重载机车牵引黏着控制半实物仿真平台研究*
2021-07-12寇树仁杨滨瑞李醒华刘佳璐
寇树仁,杨滨瑞,孙 铭,3,杨 宁,3,李醒华,刘佳璐
(1中国国家铁路集团有限公司 机辆部,北京100844;2北京纵横机电科技有限公司,北京100094;3中国铁道科学研究院集团有限公司 机车车辆研究所,北京100081)
重载机车是现代化铁路发展的重要分支之一,随着运输能力需求的不断提高,对黏着的利用提出了更高的要求,如何设计新型的黏着控制逻辑或改进现有的黏着控制逻辑以提高黏着利用效率广受业界关注。目前,国内外学者针对列车的黏着利用控制研究多是基于实际列车试验[1-2]和仿真研究[3-4]。实车试验的成本较高,且由于轮轨黏着特性受多种因素影响,其可重复性较低;仿真研究成本低,灵活性高,但是很难完全反映各环节的实际情况。因此,构建用于黏着控制研究的半实物仿真平台,在离线环境下通过接入真实的控制系统配合仿真模型,模拟列车在真实的路况中运行,对黏着控制系统的各项性能进行测试,用以验证黏着控制算法与控制逻辑的准确性和有效性将显得十分必要。
文献[5]构建了黏着控制的虚拟仿真平台,能够建立较真实的机车模型,仿真各种路况。文献[6]建立牵引传动系统实时仿真平台,能够较准确地模拟实际电动车组牵引传动系统的运行。文献[7]实现了电力机车交流传动系统的半实物闭环实时仿真,各种工况下的仿真试验表明,半实物仿真结果与地面试验结果有很好的一致性。文献[8]完成了制动控制系统半实物仿真平台硬件系统的设计和构建,有效实现了列车制动过程的半实物仿真运行。文献[9]在仿真软件中搭建列车牵引控制系统的仿真模型,对每一部分的控制策略进行了仿真验证。
文中在原有的牵引传动系统半实物仿真平台的基础上加入了通过Matlab/Simulink建立重载机车动力学模型。该模型经多体动力学模型校核后,能够模拟更多实际机车的情况,例如黏着条件变化,牵引质量,轴重转移等,真实反映机车在道路上的应用场景,为提高黏着利用策略提供了精准高效的半实物仿真环境。
1 牵引黏着控制半实物仿真平台
半实物仿真平台由上位计算机、实时仿真机、接口适配箱、TCU(牵引控制单元)等部分构成。结构如图1所示,上位计算机包括仿真机界面与司控界面,通过MVB与TCU实物相连接,通过以太网与实时仿真机连接,主要模拟司控指令、列控MVB信号、仿真机参数、模型控制;实时仿真机包括牵引传动系统模型与动力学模型。接口适配箱通过信号调理系统将仿真机的信号与TCU的信号经行适配。TCU的软硬件为真车实物。这样整个半实物可以有效的模拟列车的行驶工况和黏着条件变化。
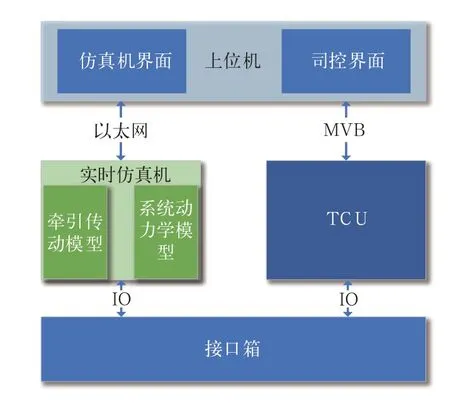
图1 半实物仿真平台组成
牵引传动系统模型包括:牵引变流器模型、牵引变压器模型、牵引电机模型,其中变流器模型又具体为预充电模型、可控整流模型、直流环节模型、逆变器模型等。
各个模型衔接关系如图2所示。
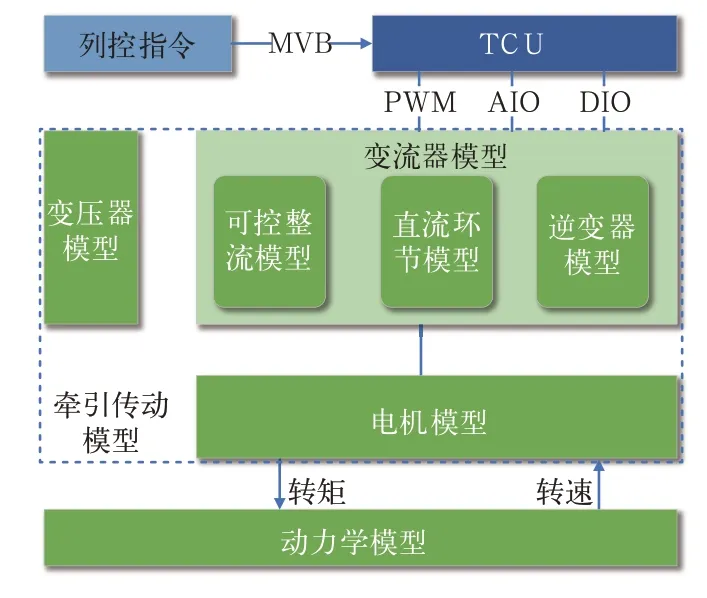
图2 模型关系示意图
在实时仿真中,整车控制器(上位机)给TCU发出控制指令,TCU根据实际情况产生控制信号控制牵引主电路,牵引主电路产生相应的电流驱动电机产生转矩,转矩信号进入动力学模型,动力学模型根据路况仿真出实时速度信号反馈给TCU进行速度闭环控制,当动力学反馈的速度信号触发黏着控制程序时TCU进行黏着控制。
2 车辆动力学模型
为了实现对黏着控制方法的仿真和验证,在Matlab/Simulink平台上构建重载机车动力学仿真模型。为证明仿真模型的正确性,使用研究列车运行安全性和动力学的SIMPACK软件对其进行验证。
不同于以往仿真系统的简单动力学模型,为了能更加真实的模拟实际路况、反映各个轴的黏着状况,构建了多轮对动力学模型、轴重转移模型、蠕滑特性模型。模拟重载机车构建了牵引质量模型等。模型框架如图3所示。
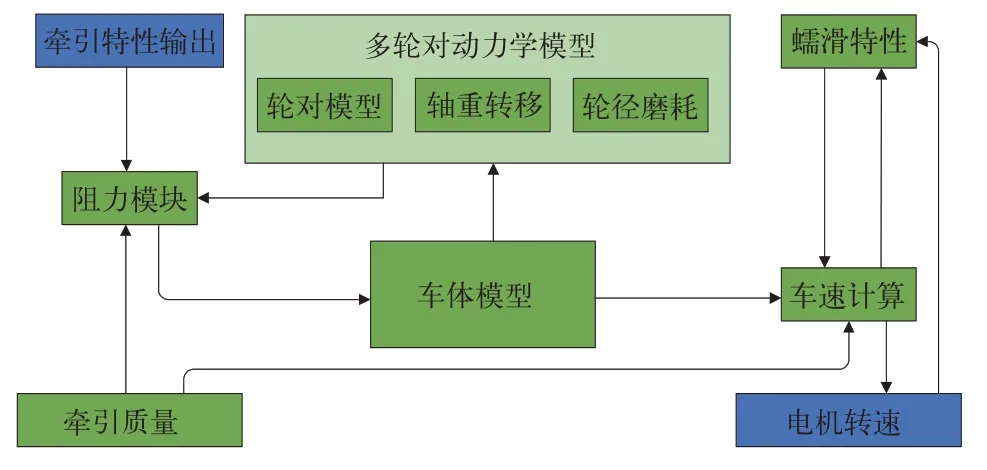
图3 动力学模型框架图
整个模型的输入量是机车各轴牵引电机输出的电磁转矩,输出量是经过仿真所得到电机转速,将电机转速反馈给TCU,使动力学模型与牵引系统模型形成一个闭环控制回路。
2.1 多轮对动力学模块
为了可以模拟在机车运行过程中各个轴所面对黏着条件的差异建立了多轮对动力学模块,多轮对动力学模块又分为轮对动力学模型、轴重转移模型、轮径磨耗系数。
2.1.1轮对动力学模型
以单个轮对为例,对其进行受力分析如图4所示,图中T为驱动力矩,N⋅m;r为轮对半径,m;m为质量,kg;F为轮周牵引力,N;v为列车运行速度,m/s;f为阻力,N;ωw为轮轴转动角速度,rad/s。根据图中的受力分析,建立轮对的运动微分方程为式(1):

图4 轮轨间车轮受力简化示意图
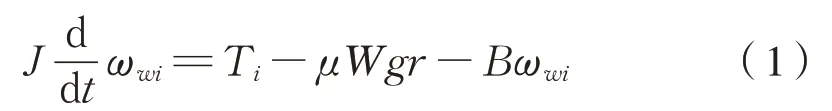
式中:T i是作用在第i个轮对上的驱动力矩,N⋅m;μWgr是轮对阻力矩,N⋅m;μ为黏着系数;W为轴重,kg;r是轮对的半径,m;g是重力加速度,m/s2;J是轮对转动惯量,kg⋅m2;B为黏滞阻力系数,kg⋅m2/s,在模型中预取值为0。
因为牵引电机输出轴的角速度和轮轴转动的角速度有关系式(2):

式中:n表示齿轮箱的传动比。
将式(2)代入到式(1)可得式(3):
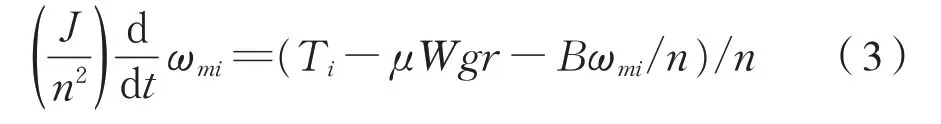
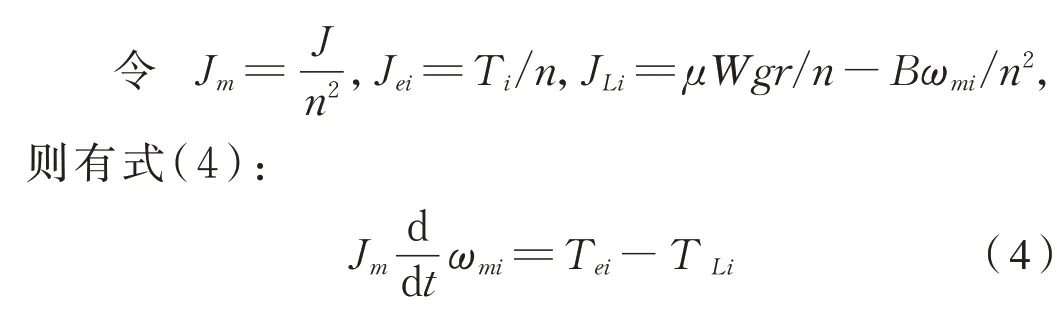
式中:Jm为电机输出轴的转动惯量,kg⋅m2;T ei为第i轴的驱动力矩,N⋅m;T Li为第i轴的阻力矩,N⋅m。
根据上式可将轮对转动的运动微分方程等效到电机端,便于各轴牵引电机电磁转矩T e的输入。
根据各轴所在位置不同,将动力学计算分别归并到对应的前、后转向架模块中,即各转向架模块中包含有与其相对应两轴的转动运动微分方程的求解。因此,在整个模型中包括了单节机车4个轮轴的转动动力学模型,能够对其中的每个轮对进行独立的运动微分方程的求解计算。如图5所示。
图5 多轮对动力学模型
2.1.2轴重转移模块
当机车产生牵引力时,各轴的轴重会发生变化,有的增载,有的减载,这就是牵引力作用下的轴重转移。我们所要计算的就是每根轴上载荷的增减量,从而计算出机车的黏着重量利用率。
在仿真模型中假设车钩不存在拉断的情况,进而对车钩力造成的轴重转移进行仿真分析。由于实际运行中,机车牵引力、牵引车钩力与轮轨黏着力之间存在垂向高度差,导致机车轴重发生轴重转移。在经过坡道时,轴重转移量加大,对黏着力产生较大的影响。为了研究列车通过坡道时产生的轴重转移量,对影响因素进行分析,如图6所示。

图6 列车轴重转移示意图
图中的主要参数分别为:L为两转向架中心距离的一半,m;L w为轴距的一半,m;h为牵引点至轨面高度,m;H为车钩至轨面高度,m;α为坡道角度,rad;F c为各轴的轮周牵引力,N。
以轮轨接触点为参考点,考虑∑ΔW i=0,即轴重转移量之和为0,可得各轴对钢轨的正压力,有式(5):
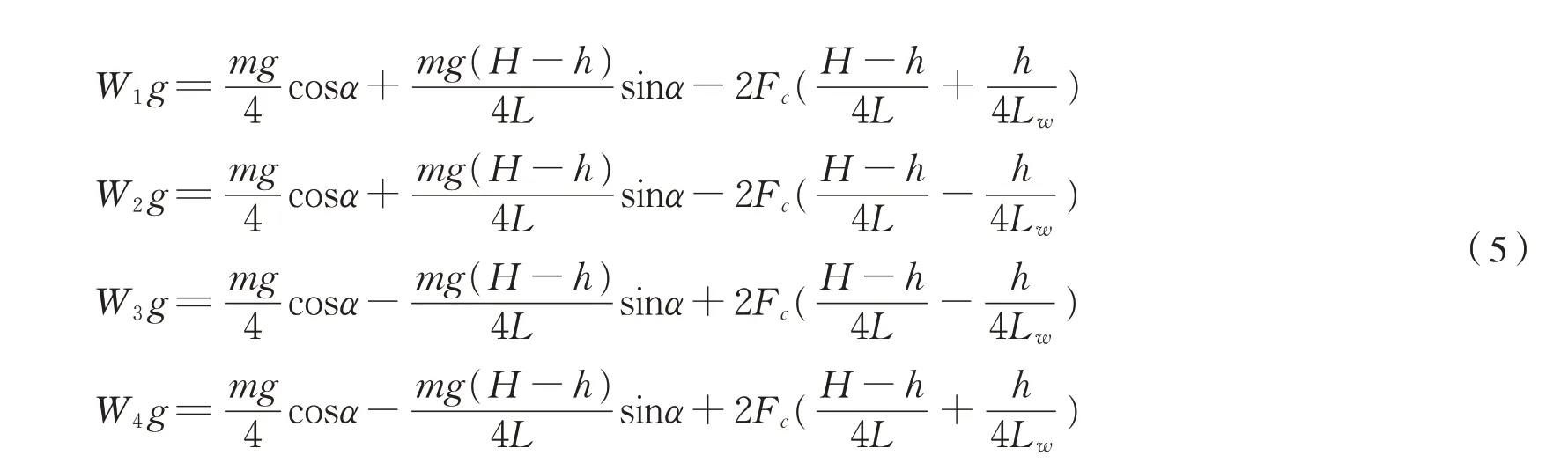
式中:mg为车重,N;W1g~W4g表示各轴对钢轨正压力,N。
根据式(5),在仿真模型中用图7所示的模块来计算机车各轴的轴重转移。
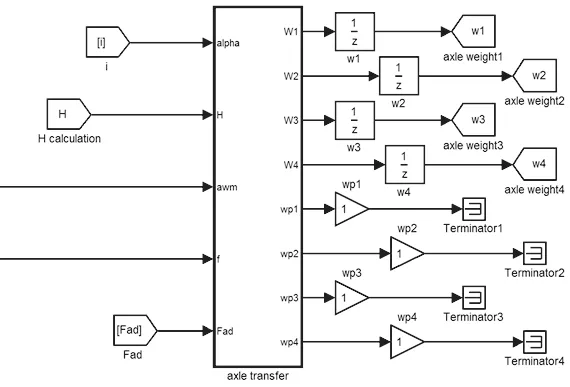
图7 轴重转移模块
2.1.3轮径磨耗系数
多轴差异性不仅体现在各轴的轴重会发生转移变化上,还体现在各轴轮径的差异上,由于轮对的旋修和自身的磨耗,还因为轴重转移的原因在牵引过程中经常前轴轴重减载,后轴轴重增载,导致前轴更容易发生空转。这些原因导致前轴的轮径和后轴有所差异。
除此之外,轮径差还会影响铁道车辆的动态曲线通过性,车辆通过曲线时,由于轮轨的原始外形不同和运用中的形状变化,引起轮轨之间的接触几何关系和接触状态的不同和变化,从而导致车轮踏面与钢轨之间存在不同程度的磨耗问题,且轮径差越大影响越明显;等值反相轮径差和前轮对轮径差则是随着轮径差的增大反而有利于铁道车辆的动态曲线通过性;而后轮对轮径差对动态曲线通过的影响不明显,仿真出来的横向力和脱轨系数曲线的规律基本是一致的。
最后,轮径的差异还会影响到车钩中心线高度的变化,严重的情况下还会导致车钩中心线超过限制值。所以为了体现机车各轴轮径的差异性,各轴的轮径乘以各自的磨耗系数,这个系数可以在模型可视化界面进行修改。
2.2 蠕滑特性模块
模型中,我们使用了基于O.Polach模型数据表的Matlab lookup-table功能的预制蠕滑率/力查询表方法。通过O.Polach模型的数据点拟合机车车速—蠕滑速度—黏着系数关系。查表方法可以省略O.Polach模型中黏着系数计算函数的计算过程,缩短仿真运行时间。根据常见轨面需求,仿真选择5种常用轨面黏着系数表格,分别为干燥撒沙,干燥,潮湿撒沙,潮湿和较差轨面状态。并且在仿真模型中可实现每一单轴所对应轮轨接触情况的设定,在80 km/h速度时蠕滑特性如图8所示,在模型中的实现如图9所示。
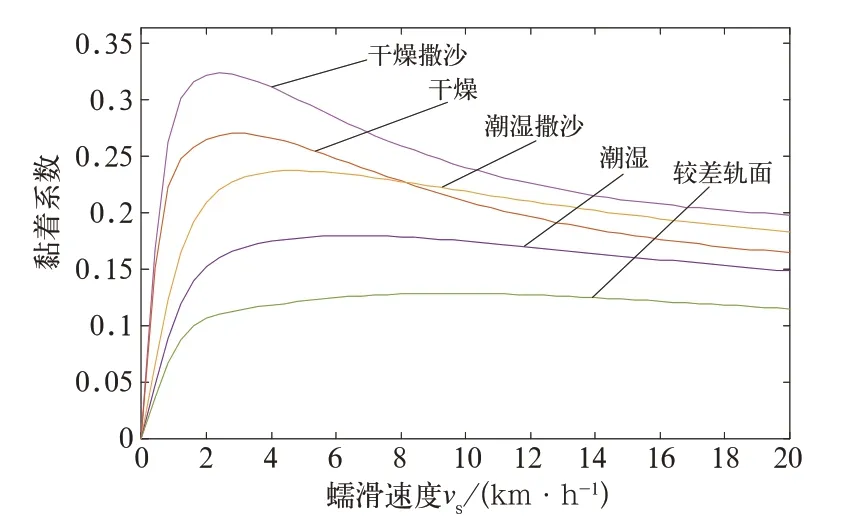
图8 蠕滑特性曲线
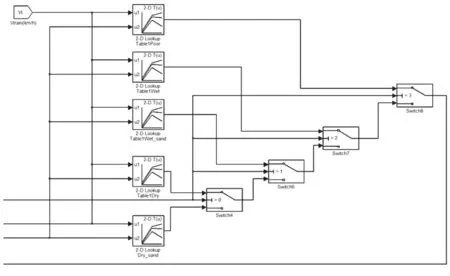
图9 不同条件轨面蠕滑率查表模块
另外,考虑到列车通过曲线时受到离心力影响,黏着接触力会发生变化。通过曲线时除了受到一个曲线附加阻力外,还考虑通过曲线半径小于550 m时黏着系数变化为式(6):
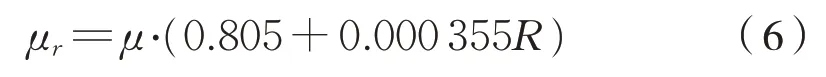
式中:μr为通过曲线时黏着系数,μ为O.Polach曲线确定的黏着系数,R为通过曲线半径,m。
在模型中主要是影响运行阻力,并通过如图10所示的模块来实现。

图10 曲线对黏着系数影响模块
2.3 牵引重量模拟模块
机车的牵引能力取决于机车的功率和牵引特性,列车在任何一个牵引区段内运行总会遇到一些长度较大、坡度不等的坡道,在这些坡道中最难通过的那一个限制了列车的最大牵引质量,称其为牵引区段的限制坡道。如果该坡道具备计算坡道的特征,即机车最终能在限制坡道上以计算速度等速运行,该坡道就叫做计算限制坡道,可以用均衡速度法计算牵引质量。
设列车在计算坡道上以机车计算速度vt(km/h)做匀速运行的条件就是作用在列车上的合力F为0,即列车运行阻力Fr与机车计算牵引力Ft乘以牵引力使用系数λ的积相等,设机车牵引质量为M w,t,则有式(7)和式(8):

式中:w″是车辆单位阻力,N/kN;w'是机车单位阻力,N/kN,可根据对应机车与车辆阻力公式得出;w i为坡道阻力,N/kN;角标i对应坡道角度i‰,根据《列车牵引计算规程》w i取近似值i,λ根据列车《列车牵引计算规程》规定取0.9[10]。
重载列车的限制坡道分为空车和重车2种,重车情况下最大限制坡道为4‰~10‰;空车情况下最大限制坡道为12‰~30‰;以重车,限制坡道为4‰,M l=100 t,vt=50 km/h,算出机车牵引质量为5 056 t。《列车牵引计算规程》规定货车牵引质量是10的整数倍,所以机车的牵引质量为5 050 t[10]。仿真模型中牵引重量的计算模块如图11所示。
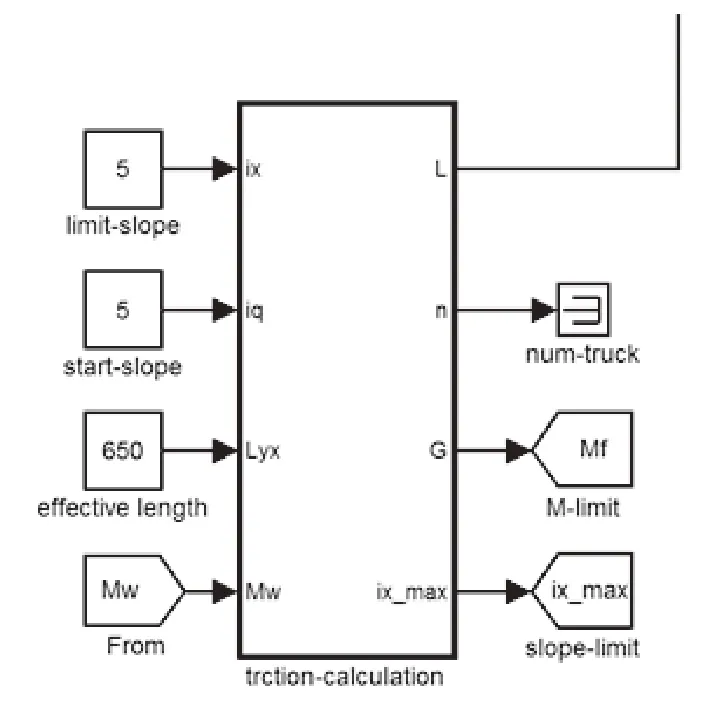
图11 牵引重量模拟模块
2.4 Simpack模型验证
为了验证基于Matlab/Simulink的动力学模型的合理性,利用了Simpack建立的精细机车多体动力学模型对仿真平台的试验结果进行校验。
将离线计算的牵引力和阻力导入到Simpack模型中后,便可在设定的仿真时间范围内计算列车运行速度的变化,并将所得的计算结果与仿真结果进行比较。其校验过程如图12所示。

图12 模型校验示意图
将图13中所示的各轴的牵引力和列车运行时所受的阻力做为已知条件,输入到所建立的Sim⁃pack精细动力学模型中做为计算条件,得到的列车运行速度曲线。将其曲线与Simulink仿真模型计算所得的速度曲线比较,如图14所示,Simulink离线仿真模型计算所得的速度曲线和精细动力学模型所得速度曲线符合很好,二者之间相差不是很大,验证了基于Matlab/Simulink的动力学模型的合理性。
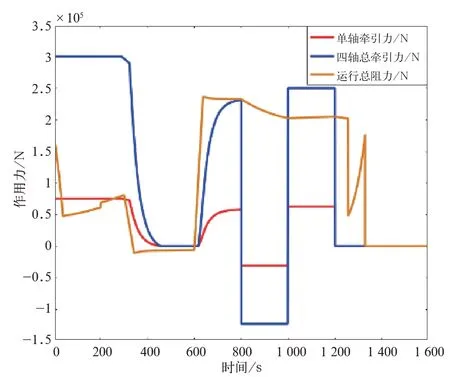
图13 离线仿真模型所输出作用于列车的力
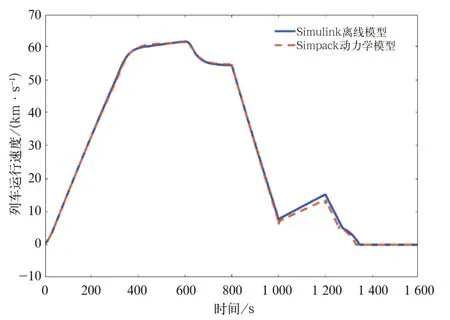
图14 多体动力学与离线仿真模型计算列车速度曲线比较
3 仿真结果分析
为了验证半实物仿真平台的有效性,基于可换装HXD1机车的国产化TCU,模拟实际线路情况设计了牵引和电制2种工况试验,由于该TCU控制2个轴,下述试验条件均为整车条件,在半实物仿真时做了匹配:
(1)电制1万t货物下坡。坡度7‰,初始速度60 km/h,电制级位维持车辆匀速,此时按照图15所示调整轨面情况,得到电制工况下黏着控制结果如图16所示。
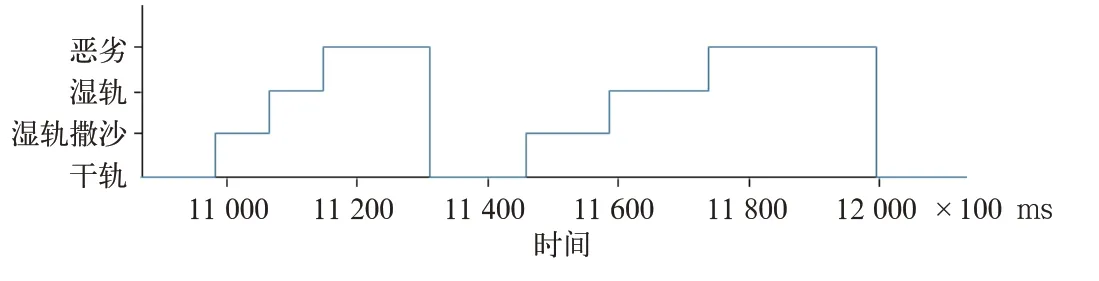
图15 调整轨面情况图
从图16中可以看出(由于制动工况,图中各数值均为负数,下面所说的数据均为绝对值的大小),改变轨面条件后,加速度增大,轮对有发生滑行的趋势,此时TCU开始进行转矩调整,减小转矩输出,加速度开始下降,随后转矩开始逐渐恢复,蠕滑速度开始波动,防滑程序通过控制输出力矩使蠕滑速度在一定范围内波动达到利用黏着力的作用,随后又再次进行了轨面条件的变化,TCU再次进行了黏着控制。最终黏着条件恢复后,也恢复了正常转矩输出。根据轨面情况的不同,控制程序将电制力控制在一个相对稳定的区间,验证了黏着控制程序的性能。
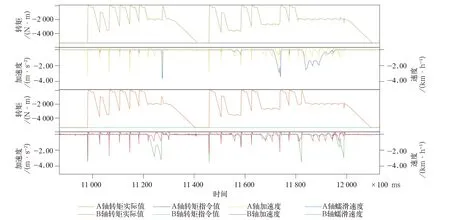
图16 电制工况黏着控制图
(2)牵引2 000 t货物上坡,坡度11‰,初始速度70 km/h,牵引级位保持列车匀速,此时按照图17所示调整轨面情况,得到牵引工况下黏着控制结果如图18所示。
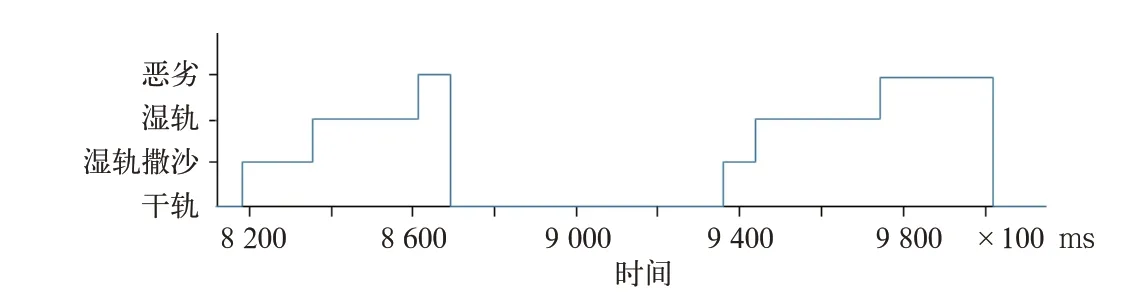
图17 轨面调整情况图
从图18中可以看出,改变轨面条件后,加速度先急剧上升,TCU检测到有空转趋势,开始进行转矩控制,随后加速度下降,随着转矩控制,蠕滑速度在区间内震荡,直至轨面条件再次发生变化。在不同的轨面条件下,黏着控制算法将发挥的牵引力控制在一个相对稳定的区间,当轨面条件恢复正常后转矩逐步恢复正常。
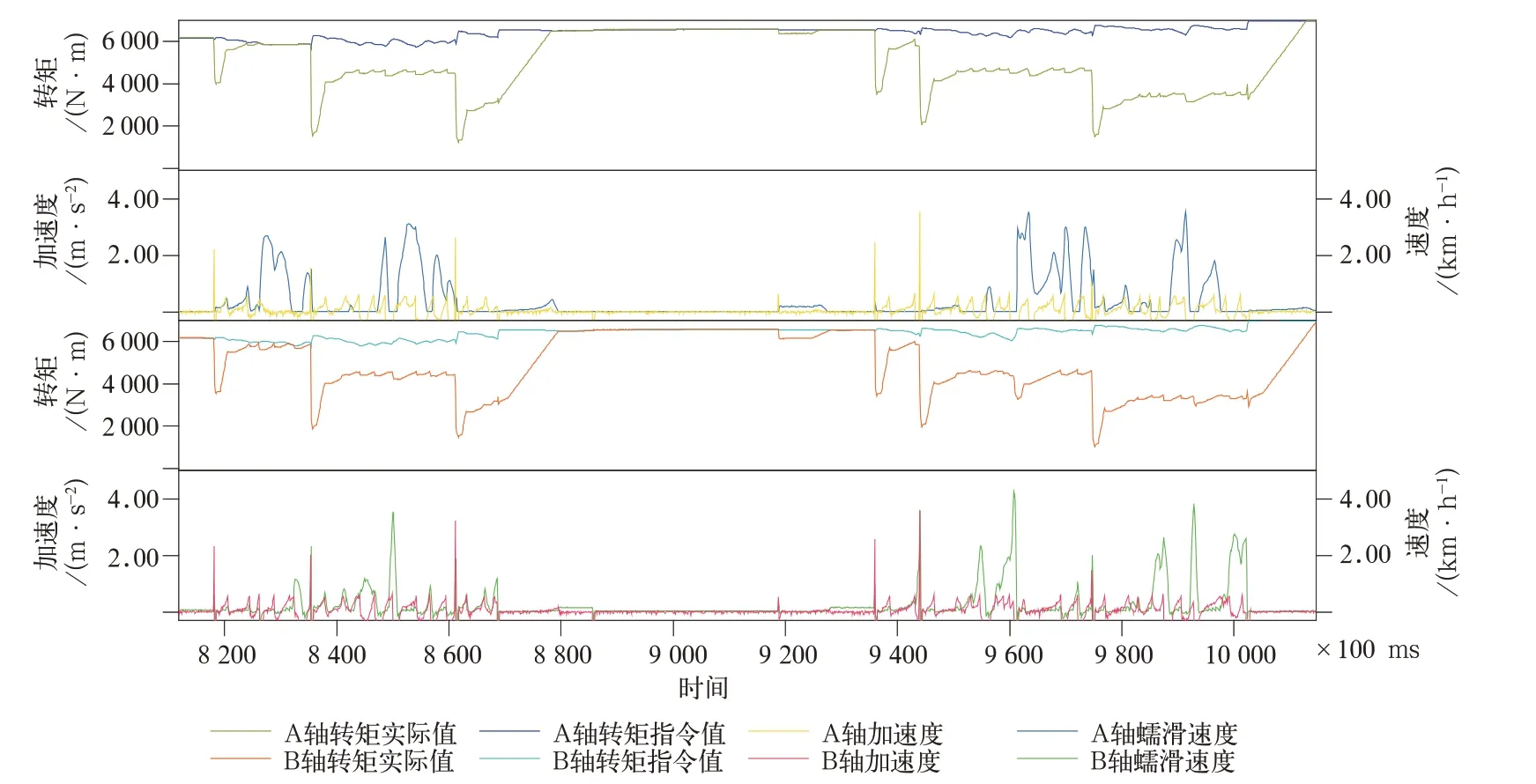
图18 牵引工况黏着控制图
4 结束语
此半实物仿真平台已投入使用,从仿真结果可以看出,系统可以模拟实时轨面情况,根据实际应用场景模拟真实列车工况,为重载机车黏着控制程序的调试与改进提供了有效的验证方法。未来平台还可以根据实际现场的数据不断地校核相关参数,使仿真环境不断地缩小与真实情况的差距。
