电力机车牵引黏着控制半实物仿真研究*

杨 宁，蒋 威，谢冰若，黄景春

（1中国铁道科学研究院集团有限公司 机车车辆研究所，北京100081；2北京纵横机电科技有限公司，北京100094；3西南交通大学 电气工程学院，成都610031）

轨道交通中电力机车是利用轮对与轨道间的黏着力来传递牵引力或制动力，实现车体的加减速运动。机车在运行过程中，轮轨间可利用的黏着力会受到实际钢轨表面状况的影响而产生难以预测的变化，当施加的牵引力或制动力超出轨面能够提供的最大黏着力，将会发生轮对的空转或滑行，造成轮轨间的剧烈磨耗，严重时甚至会造成车辆脱轨等危险后果。黏着控制作为电力机车牵引控制的关键技术，其性能直接影响到牵引力或制动力的发挥以及机车车辆的稳定行车安全。

目前，黏着控制的理论研究通常采用简化的牵引力传递模型。简化模型主要由微分和代数方程组表征，在分析和设计中不必考虑机车复杂的系统结构以及机械、电子、控制等子系统间的相互耦合关系，仅需重点考虑黏着控制方法，一定程度上降低了控制算法研发的复杂性。基于简化模型所研发的控制方案及具体算法仍处于理论实现的阶段，其有效性和可靠性需要进行详尽的试验验证后才能工程应用。黏着控制的试验研究可以在黏着试验机或机车车辆滚动振动试验台上进行，通过模拟实际行车过程中的蠕滑特性，来验证黏着控制的性能。但试验室条件下，通常只能模拟在正常轨面、水润滑和油润滑等轮轨表面状态下的黏着特性，试验工况较为有限，与实际线路情况还存在一定差别。如果在实际线路上进行行车试验，由于在实际线路上不允许列车发生持续的空转或打滑现象，部分极限工况也难以验证，而且实际线路试验需要花费大量的人力物力资源且涉及到行车安全，也难以满足对黏着控制算法进行反复研究和优化的需求。因此，研究如何快速、有效地实现黏着控制方案及算法的验证是非常必要和迫切的。

当前，硬件在环（HIL）半实物仿真作为一种快捷有效的技术手段已在电力牵引系统研发领域得到广泛应用。作为一种实时仿真方法，HIL仿真综合考虑了系统时序、动静态特性等因素，基于具体需求建立与实际环境接近的仿真机模型，通过与真实控制单元的数据交互，从而实现多参数、多运行条件的全面仿真。因此，利用HIL半实物仿真实现黏着控制方案及算法的验证是一种切实有效的方法，技术上完全可行。利用基于HIL建立的牵引系统半实物仿真平台在牵引控制单元的开发阶段可以对黏着控制算法的性能进行充分的测试和验证，降低直接进行实车试验的成本和安全风险，提高研发效率。

文中主要介绍了用于黏着控制方法地面验证的半实物仿真模型设计方法，并对此方法进行黏着控制的闭环仿真试验验证，给出了具体的仿真试验结果。

1 机车牵引黏着力利用的基本原理

黏着力是基于轮轨间的黏着特性产生的车体驱动力。大量研究分析和试验结果［1］表明，仅在轮轨接触面出现相对蠕滑的情况下，才能产生牵引力的传递。定义黏着系数μ为机车纵向牵引力与法向轴重力之比，蠕滑速度vslip为轮周速度vw与列车速度vt之差，分别为式（1）、式（2）：

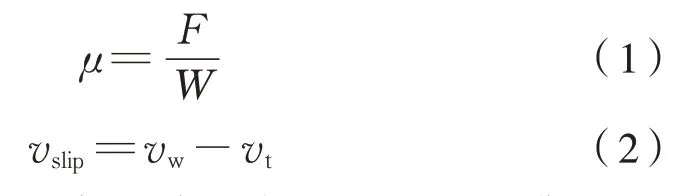
实际黏着特性通常取决于轨面的状况，典型的对应不同轨面状况的黏着特性曲线如图1所示，其中显示了正常干燥轨面对应的黏着特性曲线，和3种不同程度湿滑轨面对应的黏着特性曲线。

图1 黏着特性曲线

由图1可知，各种轨面状况下的黏着系数曲线均存在一个最大值点，在该点处黏着特性即达到最佳利用，其对应的蠕滑速度为发生空转或滑行的临界蠕滑速度。一旦实际运行时的蠕滑速度超出临界点，能够传递的牵引力或制动力将随着蠕滑速度的增加而不断减小，使动力系统失去对列车的加减速作用，如果轮周继续保持较大的转矩输出就会造成空转或滑行现象，使车辆无法处于正常的运行状态。如果空转滑行持续较长时间，对车轮和轨面均会造成较大的损伤，存在严重的安全隐患。

电力机车黏着控制的目标一是充分利用黏着特性，使蠕滑速度在临界点左侧以较小的偏差接近最佳黏着利用点，保证最大牵引力的发挥［2］；二是避免空转和滑行现象的发生，能够在不同的轨面条件下尽早的检测出空转和滑行现象或者其发生的趋势，保证行车安全。

实际工程中较多采用的黏着控制方法是组合校正法。随着控制理论的发展，一些基于智能控制理论和先进技术的黏着控制方法［3］也被提出和应用。

2 黏着控制半实物仿真模型设计

2.1 模型整体架构设计

为了实现牵引控制单元对黏着控制算法的测试需求，需要从建立单轮对动力学模型开始，逐步建立多轮对总体车辆动力学模型，并充分考虑结合机车牵引动力学系统在实际运行时遇到的各种工况及外部因素的影响，尽可能的提供与真实环境相近的被控对象。

根据机车黏着力产生的基本原理，可将黏着动力学相关模型整体上作为牵引电机的驱动负载，通过阻力力矩与牵引电机发生数学联系，模型中各模块间的整体关系如图2所示。

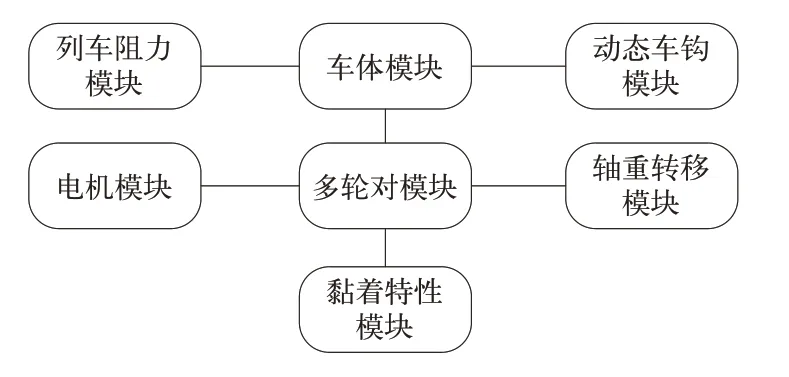
图2 模型中各模块的关系描述

电力机车主要采用轴控方式，结合半实物平台的实际情况，文中采用的单个机车牵引控制单元针对2个驱动轴的牵引电机进行控制，故黏着控制也仅与每个牵引控制单元对应的2个驱动轴相关。因此，设计的机车牵引传动系统仿真模型也包括2台牵引电机，其总体结构如图3所示。

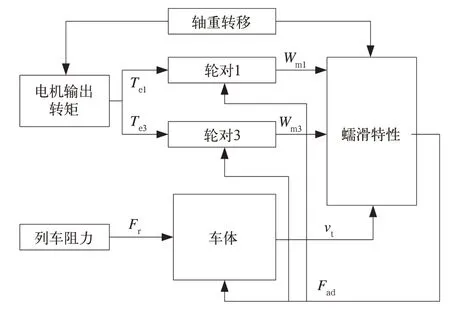
图3 黏着负载仿真模型结构

2.2 仿真模块的建模原理

（1）轮对动力学模块

列车运行过程中，牵引电机输出的力矩通过齿轮箱传递到驱动轴，在驱动轴的作用下，轮对向前滚动，如图4所示。

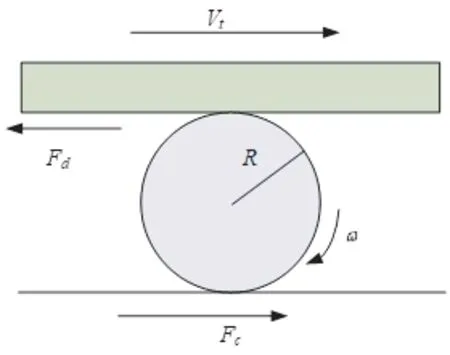
图4 轮轨间车轮受力简化示意图

根据此传递机理，建立轮对运动微分方程为式（3）：

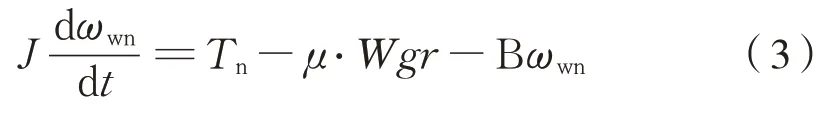
式中：Tn是作用在第n个轮对上的驱动力矩；μ⋅Wgr是轮对阻力矩，W是轴重，g是重力加速度，r是半径；J是轮对转动惯量。

设齿轮传动比为Rg，则为式（4）：

上式即将轮对转动运动微分方程等效到牵引电机端，作为各轴电机负载转矩TLn的输入。

（2）列车阻力模块

机车及货车在实际线路运行过程中，所受到的运行阻力较多，在建模过程中主要考虑了起动阻力、基本运行阻力和坡道阻力。

采用牵引规程中的计算方法［4］，机车起动单位基本阻力为ω'q=5 N/kN，货车起动单位基本阻力为ω″q=3.5 N/kN，则列车起动阻力可表示为式（7）：

式中：Mj表示牵引的机车质量；Mh表示牵引的货车质量。

机车和货车的运行单位基本阻力可分别表示为式（8）：

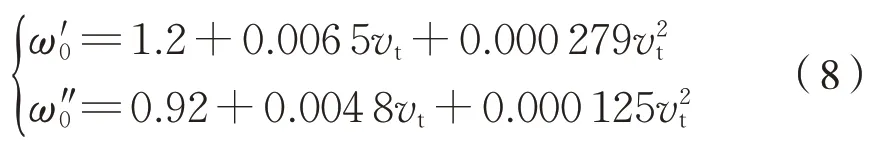
式中：vt表示列车运行速度。

列车成功起动后，若仿真模型阻力突然由起动阻力切换为运行基本阻力，则会产生一个巨大的加速度突变。实际情况下，起动后起动阻力并未立即消失，而是逐步消减至0，因此模型中的运行阻力计算公式为式（9）：

机车车辆的单位坡道附加阻力ωi，在数值上可用坡道坡度千分数i表示［4］，则坡道阻力可表示为式（10）：

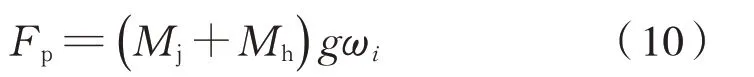
（3）车体动力学模块

列车轮轨间各轴黏着力为式（11）：

式中：μ为黏着系数；W n为轴重转移后各轴轴重。

根据机车车体运动微分方程，可将列车行驶速度可表示为式（12）：

式中：Fad（n）是各轴的黏着力大小；n表示车轴个数。

（4）轴重转移模块

半实物模型的多轴差异除了体现在轮径差异系数上还体现在轴重转移计算上［5］，轴重转移计算涉及到众多参量，方程复杂，解算耗时长。由于模型受到半实物仿真的结算时间限制，需对轴重转移模块进行一定程度的简化，机车车体的受力分析图如图5所示，其中W an是各轴轴重，A点是机车重心线与轮对中心线的交点。由于之前设定前转向架的2根轴轴重一致，所以有W a1=W a2，同理Wa3=Wa4。设WaF=2Wa1，WaB=2Wa3，在A点 对 此车体的力矩平衡方程为式（13）：

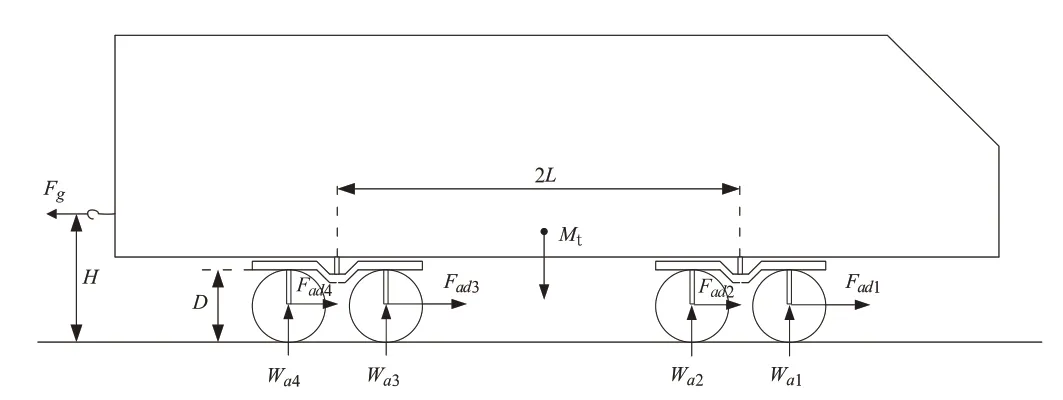
图5 机车车体受力分析图

式中：Mf、Mb分别为前、后转向架各轴总重。

仿真可解算出前后转向架不同的计算轴重，满足了轴重转移的简化计算要求。

（5）黏着特性模块

轮轨间黏着特性的建模是仿真黏着力产生的基础，也是黏着控制仿真中的关键。黏着特性模型主要有O.polach模型、Kalker系列模型、沈氏模型等。由于在研究中用于半实物仿真，需要模型具有实时性，因此文中设计了基于O.polach理论［6］和试验数据的插值查表黏着特性模型。表中的数据来源于实际的经验数据，可以模拟出几个不同等级的轨面黏着情况。在仿真试验中，为了模拟实际工况的运行效果，根据轨面状态的不同，设置5种黏着特性模型，分别是干燥撒沙轨面、干燥轨面、潮湿撒沙轨面、潮湿轨面和极差轨面。干燥撒沙轨面的黏着特性关系如图6（a）所示，干燥轨面的黏着特性关系如图6（b）所示、潮湿撒沙轨面的黏着特性关系如图6（c）所示，潮湿轨面的黏着特性关系如图6（d）所示，极差轨面的黏着特性关系如图6（e）所示。

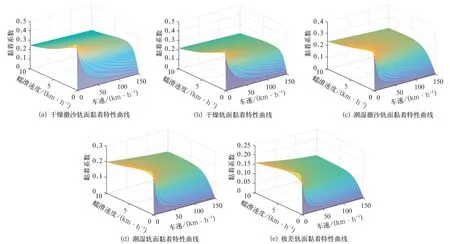
图6 不同轨面的黏着特性曲线

从以上5种黏着特性曲线可知，黏着特性是黏着系数与车速和蠕滑速度之间的关系，黏着系数随着蠕滑速度增大先增大后减小，随着车速增大而减小。上述几种黏着特性曲线代表了几种典型轨面，根据实际仿真需求可通过两条相邻黏着特性曲线进行插值得到。

3 仿真方法及结果分析

3.1 仿真方法简介

单个TCU（牵引控制单元）的仿真测试环境的核心由TCU、实时仿真机和控制上位机组成。实时仿真机中运行电气系统模型（包含变压器、变流器、牵引电机、辅助系统）和黏着控制模型（包括车体/轮对模型、阻力模型、轴重转移模型、黏着特性模型）。牵引控制半实物仿真平台的整体结构如图7所示。

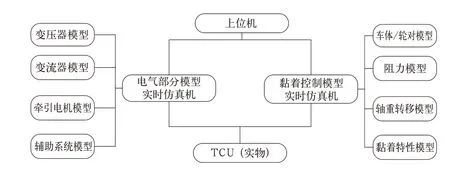
图7 半实物仿真平台结构

基于文中建立的各模块的数学方程，可通过离散化和标幺化将各方程转化为可用于编程的离散表达式，进一步得到可应用的具体仿真模型。通过上位机将建立的整个仿真模型工程编译并下载到实时仿真机中运行，即可为牵引控制单元提供实时测试环境，并且可以实时在线修改模型的基本参数。

选取不同的轮轨黏着模型，可对开发的黏着控制算法在对应模拟工况下的性能进行实时仿真验证，具体过程如下：

（1）轮轨从正常干燥转为湿滑，有空转/滑行趋势；

（2）黏着控制起作用，产生转矩减量；

（3）空转/滑行趋势得到有效抑制并尽可能利用黏着力。

黏着控制程序由TCU执行，路况切换开关可通过上位机控制，进行实时路况调整；仿真模型的关键变量可在上位机实时显示，包括轮对线速度，线加速度，轮对蠕滑速度等，便于直接监控测试过程。当路况信号发生切换时，TCU应及时检测到轮对的空转滑行趋势，若黏着控制具有良好的性能，空转/滑行趋势将会得到有效抑制并重新恢复至黏着状态。

3.2 仿真结果与分析

采用建立的黏着控制仿真模型，分别模拟列车运行过程发生牵引空转、电制滑行工况时的物理特性，对牵引控制单元及黏着控制功能进行测试验证。

牵引空转模拟的具体过程为：当机车牵引系统工作在牵引状态下，给定牵引转矩如图8所示，在升速过程中，将A轴轮轨黏着从干燥转为湿滑，空转趋势导致黏着控制算法产生转矩减量，空转得到有效抑制，当轮轨黏着从湿滑转为干燥，TCU转矩减量恢复为0，列车恢复正常运行。

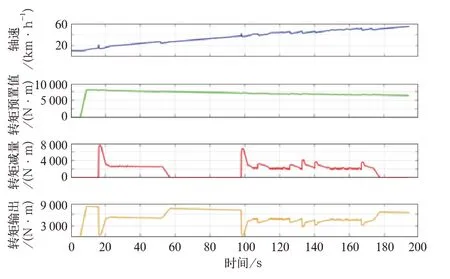
图8 牵引防空转测试

电制滑行模拟的具体过程为：在车速约80 km/h，给定电制转矩如图9所示，将A轴轮轨黏着从干燥转为湿滑，滑行趋势导致黏着控制算法产生转矩减量，滑行得到有效抑制，当轮轨黏着从湿滑转为干燥，转矩减量恢复为0，列车恢复正常运行。

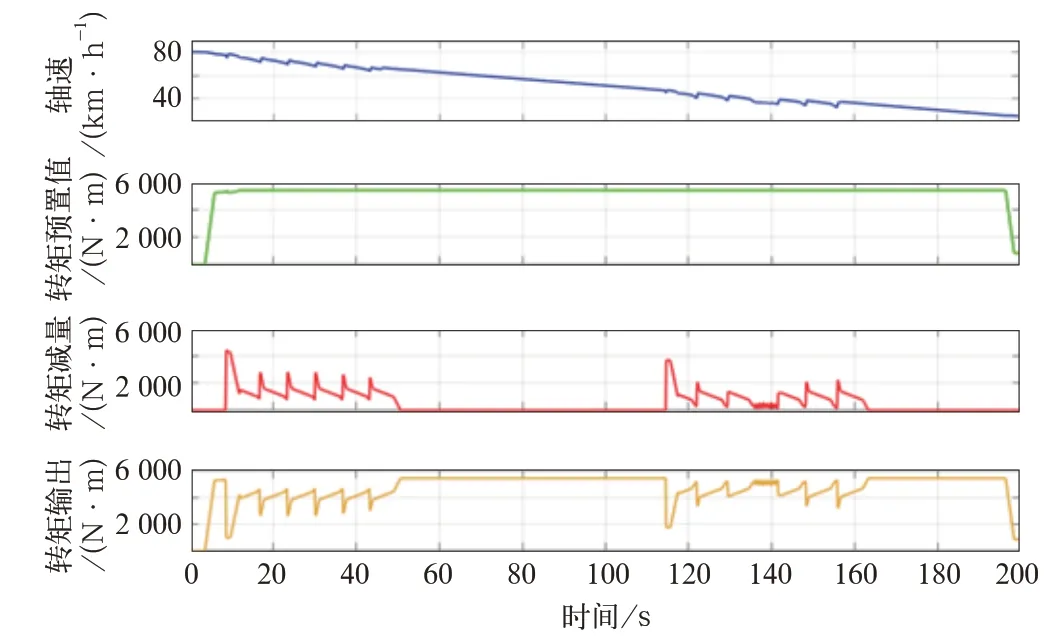
图9 电制防滑测试

完成测试后的黏着控制算法，在HXD1机车实车应用过程中单轴防空转和滑行的波形如图10、图11所示。

4 结论

在研究机车黏着利用基本原理的基础上，将黏着动力学相关模型整体上作为牵引电机的驱动负载，通过阻力力矩与牵引电机建立数学联系构建仿真模型，结合TCU、实时仿真机和控制上位机搭建了黏着半实物仿真平台。通过仿真模拟不同轨面条件，在牵引和电制工况下对黏着控制算法实现实车应用前的测试，通过完成测试后的黏着控制算法在实车的应用情况，验证了半实物仿真测试方法的可行性。由于实际车辆线路的黏着特性复杂多变，还需依据线路实际情况，不断修正和优化半实物的仿真模型，使得测试验证更为充分。