非平衡溶剂化新理论在有机染料电子光谱中的应用

苏英立，任海生，李象远

（四川大学化学工程学院,空天动力燃烧与冷却教育部工程研究中心,成都610065）

染料敏化太阳能电池（Dye sensitized solar cells，DSSCs）将太阳能转化为电能，具有成本低廉、制作工艺简单及可修饰性强等优点，在科学研究和实际应用中受到广泛关注［1，2］.如Scheme 1（A）所示，DSSCs主要由光敏电极（TiO2和Dye）和I-/I-3电解质构成.在光敏电极上，染料光敏剂（Dye）负载在二氧化钛（TiO2）半导体上，吸收太阳光子，从基态（Dye）跃迁到激发态（Dye*），使得激发态电子注入到TiO2导带中.随后，电子扩散到邻近的导电玻璃上，通过外电路到达对电极.失去电子的氧化态染料分子（Dye+）被电解液中的I-离子还原为Dye，I-离子被氧化成I-3离子，I-3离子在对电极处获得电子再还原为I-离子，从而实现光敏剂再生和电解质的重复利用.光敏剂的电子激发、转移和再生过程不断重复，产生持续的电流.

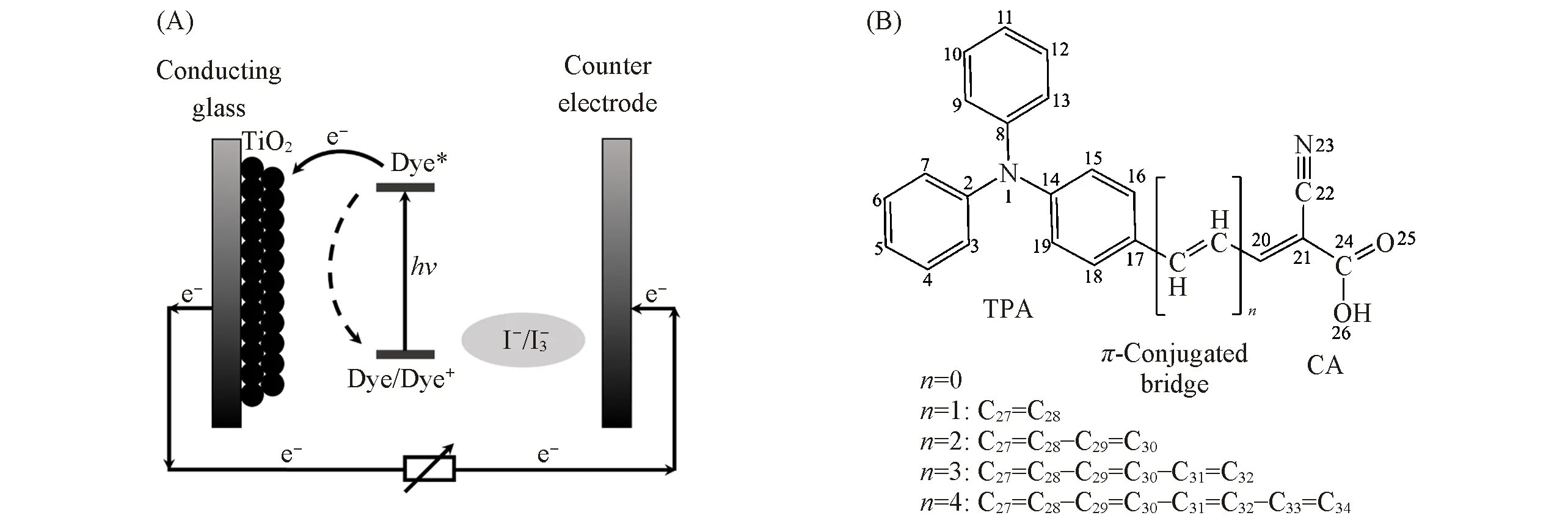
Scheme 1 Architecture and working principles of a typical DSSC(A)and dye molecular structures of TPA■CH=CH■CA(n=0—4)(B)

光敏剂主要分为金属有机配合物和无金属有机染料［1，2］.金属有机配合物通常采用贵金属钌获得较高光电转化效率［3］，但价格昂贵，对环境产生污染.而无金属有机染料具有成本低、消光系数较高及合成方便等优点，是重点研究对象.D-π-A型有机染料是一类具有代表性的无金属光敏剂，具有较高的光电转换效率［4］.D-π-A型有机染料接受光子，发生分子内电荷转移激发，电子从电子供体（D）经过π共轭桥到达电子受体（A），从而转移到TiO2导带上.根据选择的电子供体不同，有机染料敏化剂可分为三苯胺类、咔唑类和吩噻嗪类［1］.其中，三苯胺具有较强的供电子能力，其非平面结构阻碍了分子聚集，具有易成膜性和热稳定性等优点［5］.如Scheme 1（B）所示，当选择以三苯胺（Triphenylamine，TPA）为电子供体，以碳碳双键为π共轭桥，2-氰基丙烯酸（2-Cyanoacrylic，CA）为电子受体的无金属有机染料作为研究体系时，研究发现，当n=0和1时，的光电转换效率为2.3%～5.3%［6］.DSSCs的光电转换效率主要由开路电压和短路电流密度确定［3］.当电解质处于液态时，有利于电子传递，可提高DSSCs的光电转换效率.溶剂与溶质分子相互作用，从而改变有机染料的电子结构性质和光谱性质，影响其稳定性和光电性能［7～10］.

当溶质分子在溶液中发生电子转移或电子激发等超快过程时，会产生非平衡溶剂化现象，而目前国际上流行的量子化学计算软件（如Gaussian，Q-Chem等）的非平衡溶剂化模型是基于传统Marcus非平衡溶剂化理论发展的［11，12］.我们课题组［13］详细阐述了传统Marcus非平衡溶剂化理论存在的问题，并基于约束平衡原理建立了非平衡溶剂化理论，为了区分将该理论称为非平衡溶剂化新理论.本文首先总结非平衡溶剂化新理论在吸收光谱和发射光谱中的数值解计算，并将其应用于乙腈溶剂中有机染料光敏剂的光电性质研究.

1 非平衡溶剂化新理论

自然界中大多数的化学反应都是在溶液中进行，溶剂既可作为反应物，也可作为环境介质影响化学反应，决定反应能否发生和反应快慢等.如Scheme 2（A）所示，1956年，Marcus［11，12］通过两步线性充电的方式研究了超快（溶质电子转移/激发）过程中的溶剂化效应，引入非平衡态，并对平衡态到非平衡态的过程采取可逆功积分方法，推导了的非平衡态N的溶剂化自由能，建立了非平衡溶剂化理论.其中，ρ和Φ分别为溶质电荷密度和溶质-溶剂体系的总电势，“eq”和“neq”分别为体系处于平衡态和非平衡态.Φ为溶质电荷产生的电势ψ和溶剂极化产生的电势φ之和.εs和εopt分别为溶剂的静介电常数和光介电常数.ΔΦop是在第2步线性充电的过程中电荷Δρ在εopt的溶剂中产生的总电势.然而大量研究发现该理论得到的溶剂重组能明显高估实验拟合值，使得计算电子转移反应的速率常数偏低［14，15］.我们发现该理论存在问题：热力学原理表明在平衡态1与非平衡态N之间不存在可逆途径，因此采用可逆功积分推导的非平衡溶剂化自由能不准确.

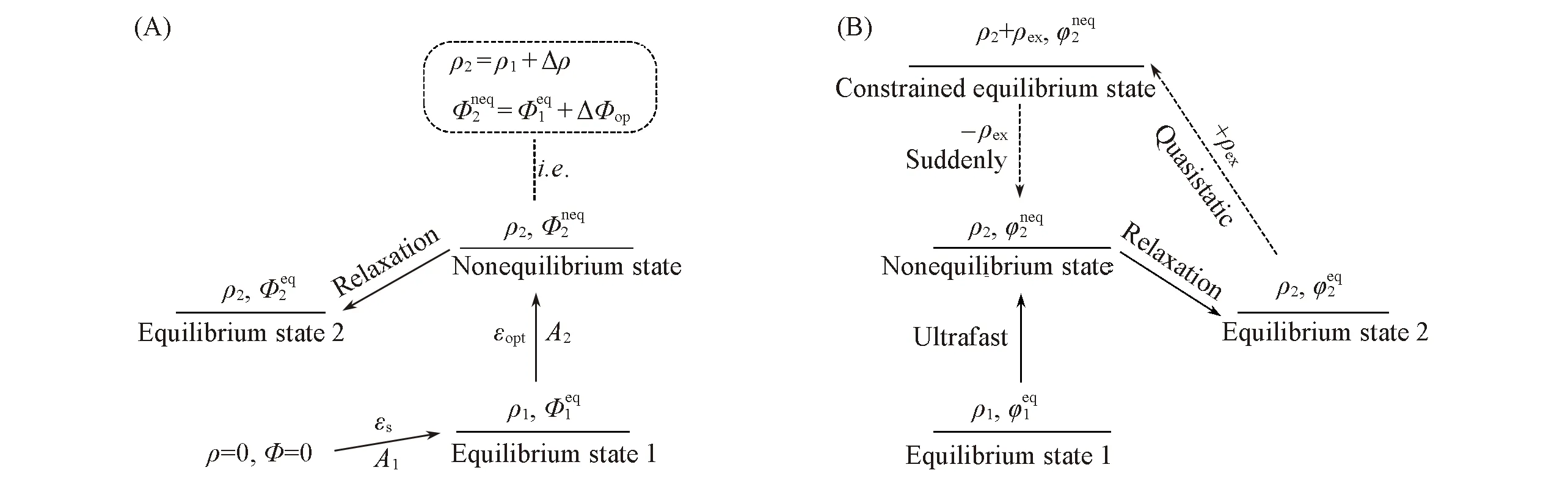
Scheme 2 Schematic diagrams of the reversible work integration method(A)and the constrained equilibrium approach(B)

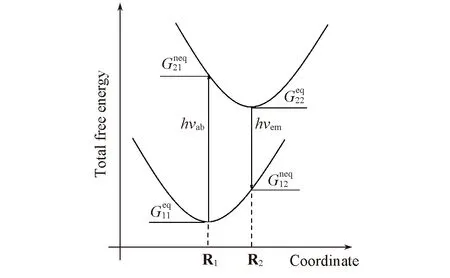
Scheme 3 Schematic depiction of vertical absorption and emission processes

基于经典热力学的方法，Leontovich［16］提出可利用约束平衡态方法来处理非平衡态体系.本课题组［13，17～19］采用该约束平衡原理，构建了溶剂化效应体系的约束平衡态其关键步骤是引入适当的约束外场或外加电荷ρex，当无摩擦地迅速撤去外场或外电荷后，体系恢复到真正的非平衡态而约束平衡态是平衡态，可通过经典热力学方法求解约束平衡态与其它任意平衡态之间的相互作用及状态函数的变化量.

以溶剂为研究体系，溶质电荷及其它外电荷视为环境，通过分析溶剂极化电势φ与溶质电荷ρ之间的相互作用来解析非平衡溶剂化现象.根据电动力学公式，平衡态的静电溶剂化自由能（Feqi）的表达式为

式中：i为研究体系处于平衡态1（i=1）或平衡态2（i=2）；V表示积分为全空间.采用可逆准静态的方式，将约束电荷ρex线性叠加到平衡态2上，相应地极化电势由φeq2变为φneq2，构造约束平衡态C[ρ2+ρex，φneq2].这个过程研究体系（溶剂极化）与环境（溶质电荷与约束电荷之和）始终保持平衡.由于这个过程是可逆的，所以平衡态2到约束平衡态C所做的功为

其中，

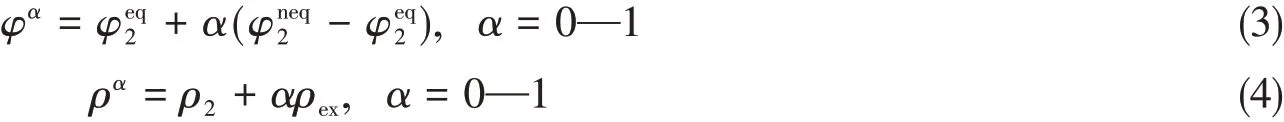
所以

从而得到约束平衡态C的静电溶剂化自由能：

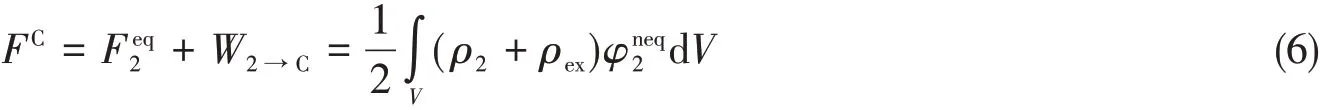
因为约束平衡态是平衡态，所以也可直接根据电动力学的平衡溶剂化自由能公式得到式（6）.当体系处于约束平衡态C时，无摩擦地迅速撤去外加约束电荷ρex，体系回到非平衡态N.体系从约束平衡态C到非平衡态N所做的功为

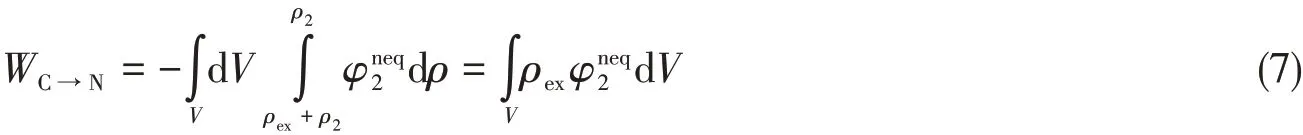
则非平衡态N的静电溶剂化自由能为

式（8）是基于经典热力学的约束平衡原理推导的非平衡溶剂化自由能表达式，从而建立了非平衡溶剂化新理论.

基于极化连续介质模型（PCM），采用溶质静电势（V）、外加电势（Vex）和溶剂极化电荷（Q）的形式，可得非平衡态N的静电溶剂化自由能的数值解公式为

式中：V2，m为在溶质空穴第m个面元上的溶质静电势为非平衡态N的溶剂极化电荷.基于PCM的线性公式（DQ=V），体系处于约束平衡态时的溶质静电势和溶剂极化电荷之间的关系为

将式（10）带入式（9）中，则非平衡态N的静电溶剂化自由能的数值解形式为

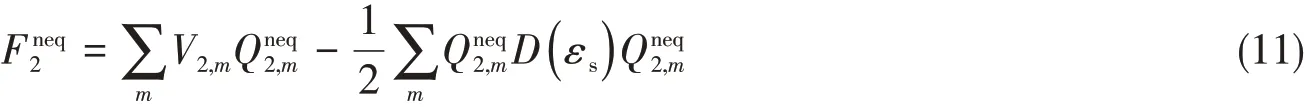
式中：方阵D(εs)与PCM的特定模型和溶剂性质有关.

2 垂直激发能和垂直发射能的数值解

如Scheme 3所示，根据Frank-Condon原理，溶液中体系的垂直激发能和垂直发射能分别为

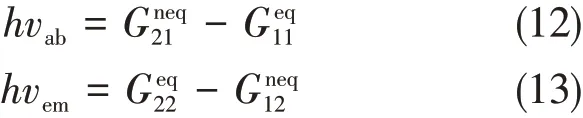
式中，Gij为研究体系的总自由能；i为电子基态（i=1）或电子激发态（i=2）；j为体系处于基态（j=1）或激发态（j=2）平衡几何结构Rj.“eq”为溶剂极化和溶质电子密度分布保持平衡，而“neq”为溶剂极化和溶质电子密度分布还未达到平衡.体系的总自由能可以进一步表示为

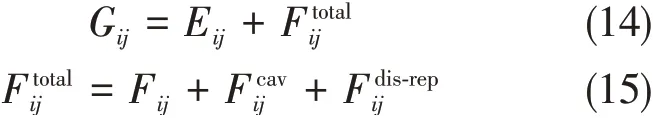
式中，Eij为溶质处于基态（j=1）或激发态（j=2）平衡几何结构Rj在基态（i=1）或激发态（i=2）时的电子能量为总的溶剂化自由能，包括静电溶剂化自由能F ij，孔穴能和色散-排斥能在垂直激发或发射过程中，溶质结构未发生变化，则孔穴能在该过程中保持不变.色散-排斥项在强极性溶剂中电子跃迁前后的贡献几乎相等［20］.则当溶质电荷密度发生变化时，溶剂化自由能变化几乎均来自溶质-溶剂静电相互作用.所以，在接下来的电子跃迁能计算中的溶剂化作用仅考虑静电溶剂化自由能F ij.对于非平衡溶剂化，采用上述非平衡溶剂化新理论来推导溶液中垂直激发能和垂直发射能的数值解表达式.

2.1 垂直激发能

使用自洽态特定（State-Specific，SS）方法，结合含时密度泛函理论（TD-DFT）和PCM获得溶液中垂直激发能的表达式.基态和激发态的能量差ω可以通过解TD-DFT的无规相近似方程（Random-phaseapproximation equation，RPA）得到：

式中：ω为RPA方程的本征值为跃迁本征矢量，而矩阵A和B通过基态轨道和相应的轨道能量计算得到［21，22］.当分子轨道由激发态反应场确定时，溶剂效应隐性地包含在分子轨道和轨道能量中.所以，式（16）计算的基态与激发态的能量差ω为

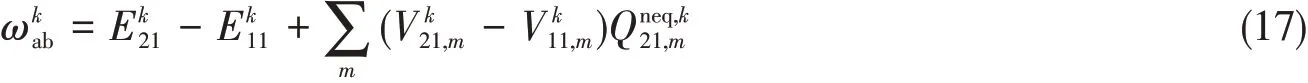
式中，k为非平衡激发态反应场迭代次数；分别为第k次迭代时，体系处于基态和激发态时在溶质空穴第m个面元上的溶质静电势.所以，结合式（11），式（14），式（15）和式（17），体系处于非平衡激发态时的总自由能为

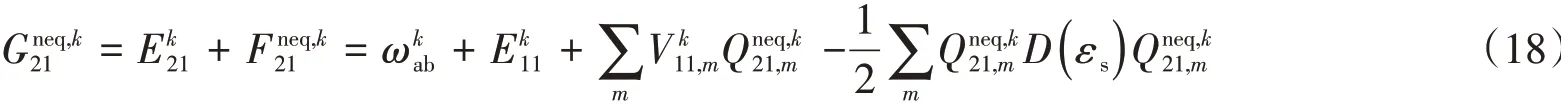
将式（1）、式（14）和式（18）代入式（12）中，得到：

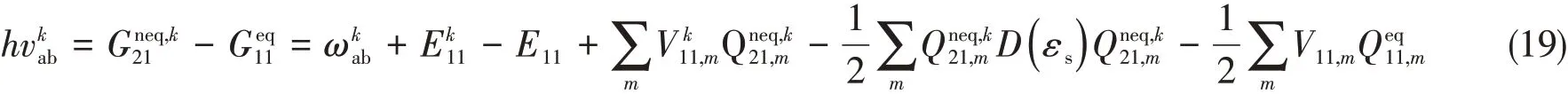
式（19）为基于约束平衡原理，通过自洽SS-PCM/TD-DFT方法得到了溶液中垂直激发能的数值解公式.在迭代过程中，非平衡激发态反应场由激发态快极化电荷和慢极化电荷组成.并且，激发态慢极化电荷始终保持不变，等于基态慢极化电荷，而激发态快极化电荷随着激发态电子密度不断迭代更新，直到非平衡激发态反应场收敛.

2.2 垂直发射能

溶液中的垂直发射能的数值解仍然通过自洽SS-PCM/TD-DFT方法获得.发射过程的TD-DFT计算所需要的分子轨道和轨道能量由平衡激发态反应场确定，所以基态和激发态的能量差为

结合式（1）、式（14）、式（15）和式（20）可以得到平衡激发态的总自由能为

在整个计算过程中，激发态电子密度和平衡激发态反应场不断迭代更新，直到平衡激发态反应场收敛，从而获得平衡激发态的总自由能.与垂直激发过程类似，基于非平衡溶剂化新理论，可以获得非平衡基态的溶剂化自由能：

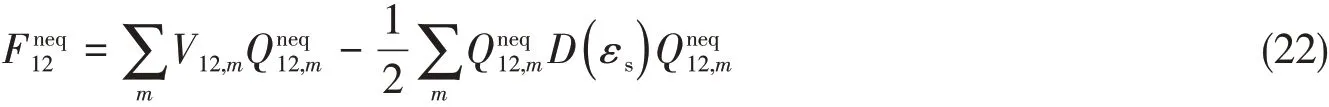
所以，非平衡基态的总自由能为

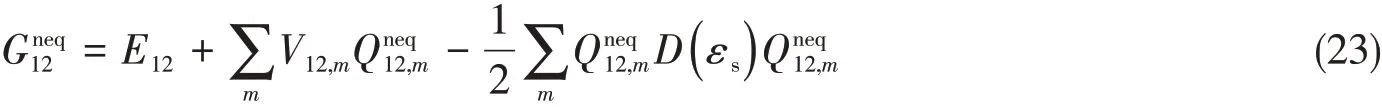
在基态自洽反应场计算过程中，非平衡基态反应场由基态快极化电荷和基态慢极化电荷组成.非平衡基态慢极化电荷等于上述自洽收敛的平衡激发态的慢极化电荷，而非平衡基态快极化电荷来自于基态电子密度的快极化电荷.最终，垂直发射能的数值解表达式为

3 结果与讨论

3.1 电子结构性质

在ωB97X-D/6-31+G*水平下，分别优化了在真空和乙腈溶剂中有机染料4）的基态和第一单重激发态平衡结构.表S1（见本文支持信息）列出了有机染料（n=0～4）的基态和第一单重激发态平衡结构分别在真空和乙腈溶剂中的键长、键角和二面角（φ，°），二面角的正负仅代表该二面角的方向.计算结果表明，当n=0～4时，溶质分子的对应几何参数非常相似，说明π共轭桥上碳碳双键的加长并不影响溶质分子的整体构型.但是，极性溶剂会一定程度地改变溶质分子的平衡几何结构，特别是对激发态几何结构的改变.在气相中，当分子从基态跃迁到第一激发态，与基态结构相比，激发态结构的TPA电子供体部分的键长（d1-14）减小，CA电子受体部分的键长（d20-21）增加.在乙腈溶剂中，溶质分子从基态跃迁到第一激发态的分子结构变化更大.除了TPA部分，其它所有原子几乎在同一个平面上.三苯胺电子供体的特殊非平面立体结构可以抑制溶质分子间的π-π堆叠，在一定程度上阻止染料溶质分子的聚集.φ7-2-8-9为TPA左侧两个苯环之间的二面角.当n=0～4时，基态（激发态）溶质分子在真空中的φ7-2-8-9分别为-79.116°（-65.877°），-79.485°（-69.707°），-77.283°（-74.483°），75.684°（77.169°）和74.637°（78.670°）；而在乙腈溶剂中的φ7-2-8-9分别为-85.456°（-73.106°），-84.056°（-77.931°），-80.525°（-83.337°），77.720°（86.811°）和75.850°（88.851°）.所以，随着π共轭桥上碳碳双键的增加，基态的二面角φ7-2-8-9呈减小的趋势，激发态呈增加的趋势.而乙腈溶剂增大了二面角φ7-2-8-9，有利于染料分子在溶液中的分散.

Table 1 Dipole moments(10-29 C·m)for equilibrium ground states(EGS),nonequilibrium excited states(NES),equilibrium excited states(EES),and nonequilibrium ground states(NGS)of in vacuum and acetonitrile*

Table 1 Dipole moments(10-29 C·m)for equilibrium ground states(EGS),nonequilibrium excited states(NES),equilibrium excited states(EES),and nonequilibrium ground states(NGS)of in vacuum and acetonitrile*

*R1 and R2 represent the equilibrium ground and excited state geometries（Scheme 3），respectively.

?

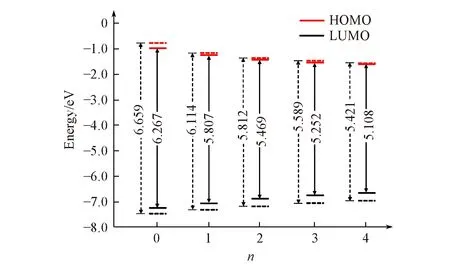
Fig.1 HOMO and LUMO energy levels of in vacuum(dash lines)and acetonitrile(solid lines)

3.2 电子吸收和发射光谱

Table 2 Vertical excitation energy(hv ab)and oscillator strengths(f)of the S0→S1 transition with the amplitudes of the HOMO→LUMO(H→L)transition

Fig.2 Absorption(A)and emission(B)spectra of in vacuum(dash lines)and acetonitrile(solid lines)

影响光谱移动的主要因素是溶质几何结构变化和溶质-溶剂之间的静电溶剂化自由能.通过前面计算发现，溶剂对有机染料分子的几何结构有一定的影响，因此本文利用了在溶剂中优化的几何构型，考虑了由几何结构变化对光谱移动的贡献.非平衡溶剂化新理论主要基于溶质-溶剂之间的静电溶剂化自由能来获得垂直激发能［式（19）］和垂直发射能［式（24）］的表达式，用来研究有机染料光谱移动和Stocks位移.

Table 3 Vertical emission energy(hv em)and oscillator strengths(f)of the S1→S0 transition with the amplitudes of the LUMO→HOMO(L→H)transition as well as the corresponding Stokes shifts(Δλ)

4 结 论

总结了非平衡溶剂化新理论和在量子化学软件Q-Chem中基于TD-DFT实现溶剂效应下计算电子吸收和发射光谱的数值解方法.研究了有机染料在真空和乙腈溶剂中的电子结构和光谱性质.发现随着π共轭桥上碳碳双键个数的增多，垂直激发能降低，光捕捉效率和Stokes位移增大，所以在本文中是最优的DSSCs光敏剂.相比于真空条件下，乙腈溶剂使得电子光谱发生红移，Stokes位移增大，有利于调节的光谱性质，从而获得更大的光电转换效率.有助于理解溶质电子结构与光谱性质的关系，有助于有机染料光敏剂的设计与合成.

支持信息见http：//www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20200805.