PBFC-PI量子动力学方法及应用

边文生，曹剑炜

（1.中国科学院化学研究所,北京分子科学国家研究中心,北京100190；2.中国科学院大学化学科学学院,北京100049）

1 Introduction

Quantum dynamics（QD）calculations of polyatomic systems are crucial in many fields，however，it remains a challenge to extend such calculations to molecular systems with more than six atoms［1—4］.The most important factor that impedes the QD calculation using a basis set representation of a Hamiltonian，is that the size of Hamiltonian increases exponentially with the number of atoms.So we need to develop efficient iterative methods for computing energy levels，wavefunctions，and etc.

The process-oriented basis function customization（PBFC）-parallelized iterative（PI）method is an efficient QD method developed by Bian’s group.The basic idea of PBFC is proposed in our recent work［5］.The PBFC-PI method aims at treating the nuclei in a molecular system with quantum mechanics in the time-independent formalism using the direct expansion method，which is different from the most popular QD method currently available，or the multi-configurational time-dependent Hartree（MCTDH）approach［6，7］.The latter makes use of the variational principle and adopts a time-dependent formalism.The advantage of solution of the many-body schrödinger equation using the direct expansion method has been demonstrated by Bian and Deng in the hyperspherical coordinate formalism［8，9］.

The PBFC-PI method has been applied in the study of vibrational spectra，lifetimes of reactive intermediate，tunneling splittings and rates of H transfer.In particular，tunneling splittings are very important observables in lots of chemical and biological systems and have attracted great interest in recent years［10—14］.Tunneling splittings can provide direct and valuable information about lifetime and rate of an isomerization process，which is achievedviaH transfer［15］（see Fig.1）.For example，the tunneling splittings can be produced by tunneling between two vinylidene wells through the intermediate acetylene well，and this process is realized by sequential double H transfer.The isomerization involves two carbon permutation isomers of vinylidene，and can be investigated by permutation tunneling splitting.The PBFC-PI method in combination with other methods has been applied in studies of a few benchmark reactive systems，and the calculational results are important in revealing the essential characteristics of the H transfer processes.In particular，we have performed efficient QD calculations of tunneling splittings in malonaldehyde（MA）［3］，the formic acid dimer（FAD）［15，16］，and vinylidene（-d2）［5，17］.We have achieved the first accurate time-independent QD calculations on MA in full dimensionality and the work demonstrates that our method is conceptually simple and easy to implement.Our studies on FAD have yielded calculational results in much better agreement with experiment than the previous theoretical studies.We have also achieved accurate QD calculations［5，17］of vibrational states and tunneling splittings for vinylidene（-d2）and analyzed the peaks shown in the cryo-SEVI spectra［18］obtained very recently.

Fig.1 Schematic potential energy profile along the H-transfer path in the formic acid dimer,with the tunneling for both the vibrational groundand excited-states indicated[15]

2 The PBFC Method

The PBFC is a strategy/technique proposed recently by Bian［5］and its main idea is to customize basis functions for specific physical/chemical process，which is often achieved by optimizing and adjusting then-dimensional（nD）effective Hamiltonian and the coordinate ranges.Then the information about specific physical/chemical process such as the H transfer isomerization is included into the basis functions.Our previous calculations indicate that，this method is able to greatly reduce the required overall basis size for a given accuracy and evidently increase the efficiency of the following iterative procedure for solving the eigenvalue problem.In many cases，what we need is optimizing and adjusting thenD effective potential（EP）part of an effective Hamiltonian.In practice，we construct the zeroth-order ofnD EPs by following the minimum energy reaction path on the potential energy surface（PES）.This is understandable since normally the minimum energy reaction path is energetically favored in a chemical reaction.For example，to customize basis functions for the H transfer process，the zeroth-order ofnD EPs may be generated from the realistic PES by smoothly connecting two parts：the first part is yielded by following the steepest descending path starting from the saddle-point for H transfer，whereas the second part is produced by minimizing the potential with all the remaining degrees of freedom（DOF）.Then，the zeroth-order EP needs to be further adjusted according to the analysis on changes of all coordinate variables during the H transfer process.In the following，we discuss the PBFC method in the context of 1D，2D，and 4D EPs，respectively.

2.1 1D Effective Potential

In the study of H transfer issue，the 1D EP is customized for the H transfer process attracting our interest.For example，in the FAD case，the typical 1D Eps［16］are shown in Fig.2，and are obtained in the following way.The 1D EPs for the modesQ1andQ3are obtained by smoothly connecting three parts：the central part is yielded by following the steepest descending path starting from the isomerization saddle-point，whereas the parts on the two sides are produced by minimizing the potential with all the remaining DOF.The 1D EPs for the modesQ6andQ8are generated by minimizing the full-dimensional PES with all the remaining DOF，respectively.When strong anti-symmetric couplings between the modes and reaction coordinate are encountered，such as that betweenQ1andQ3，we should follow the former method，whereas in other cases，the way used for the modesQ6andQ8can be followed.

Fig.2 1D effective potentials for Qi(i=1,6,3,8)in formic acid dimer[16]

In addition，the tunneling splitting of MA results from the H transfer between the two equivalent wells，and in normal coordinates at the saddle point，Q21is identified as the H transfer reaction coordinate.Based on the basic idea of our PBFC method，each 1D EP and its coordinate range are customized for the H tunneling process.In particular，the normal coordinate range of each 1D EP forQi（i=1，…，20）is chosen in such a way that it just bounds the lowest five vibrational energy levels，whereas a much larger coordinate range is used forQ21，sinceQ21involves large amplitude motion of the H atom.The normal coordinate ranges determined in this way for all 21 modes can be found in Table III of ref.［3］.The 1D EPs for all 21 normal modes of MA are generated in the similar way as described above，in which the 1D EP forQ21shows a double-well structure with a reasonable barrier height，and this is important for the study of tunneling splitting.

2.2 2D Effective Potential

Typical contour plots of the 2D EPs used in our FAD calculations［15］are shown in Fig.3，which are as functions ofQ1andQiand obtained through the procedures described above.Similar to that discussed in the last subsection，the coordinate ranges are also customized for the double H transfer process.For example，when the potential is minimized with respect to all the remaining coordinates，the optimized ranges for the coordinates of in-plane vibrational modes are set much larger than those for the coordinates of out-of-plane modes，since the double H-transfer process mainly occurs within the plane.

Fig.3 Contour plots of the 2D effective potentials as functions of normal coordinates Q1 and Qi(i=9,8,22,21,5,3)[15]

2.3 4D Effective Potential

Here the PBFC method is demonstrated in the case of 4D EP in the benchmark vinylidene-acetylene isomerization system.To give a better description of the sequential double H（D）transfer isomerization，the zeroth-order of the 4D EPs are generated from the original PES by minimizing the potential with respect tor1andr2［17］（see Fig.4），ensuring that non-relevant pathways such as the concerted double H transfer are ignored.The final 4D EP is obtained by modifying the zeroth-order 4D EP，according to whether it is relevant during the sequential double H（D）transfer process.In particular，there are configuration regions corresponding to the simultaneous migration of both H（D）which are removed.The deep well region of acetylene is far away from the H（D）transfer path，which can be omitted.The obtained 4D EP generated in this way is able to properly cover the vinylidene，transition state and acetylene regions，and a typical cut［17］is shown in Fig.5.It is clear that the 4D EP is smooth，and oriented towards the sequential double H（D）transfer process.

Fig.4 CC-DD Jacobi coordinate[17]

3 Coordinate Representation and Matrix Equation

It is important to choose a suitable coordinate representation for a specific application.Jacobi coordinates are often preferred.For example，there are three kinds of orthogonal coordinate representation which can be used to describe the vibrational motion of vinylidene，namely，the CH-CH Jacobi coordinates，CC-HH Jacobi coordinates，and orthogonal satellite coordinates.The CC-HH，or CC-DD Jacobi coordinates（see Fig.4）are chosen in our study，since this coordinate system has the advantage that the full permutation and parity symmetries can be easily exploited.The hyperspherical coordinate is a powerful orthogonal coordinate system，using which the direct and analytic solution of the many-body Schrödinger equation is achieved by Bian and Deng［8，9，19］.Furthermore，the normal mode coordinates are beneficial for larger molecular systems.In the following，some theoretical details are demonstrated using the normal mode and Jacobi coordinates.

3.1 Normal Mode Coordinate Representation

For anN-atom nonlinear system，the normal mode Hamiltonian has the following form，

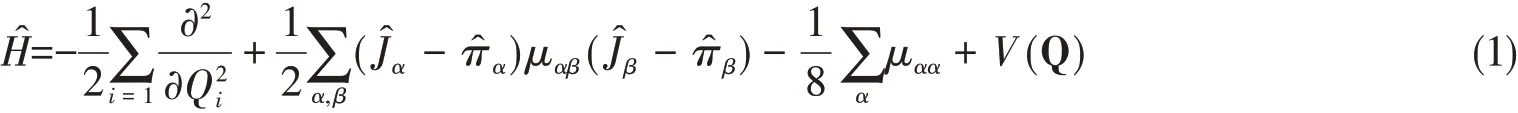
where Q denotes a collection of theM=3N-6 normal coordinates，Jis total angular momentum，andμαβis the inverse of the effective moment of inertia tensor.From the left to right in order，the four terms are the standard kinetic energy operator，vibrational angular momentum（VAM），so-called“Watson”term，and PES respectively，where

In the studies of the H transfer issue，normally we choose the normal coordinates at the saddle point.Since the VAM terms only have very small influence on the zero point energy and ground-state tunneling splitting（Δ0），they can be added separately.

The discrete variable representation（DVR）［22—24］basis functions are often used.The wave function can be expanded by the direct product of 1D DVR，

whereπj i(Q i)andNiare the 1D DVR basis function and basis size forQi，respectively.The 1D DVR basis functions are obtained by a unitary transformation from the truncated eigenfunctions of a designed 1D effective Hamiltonian

whereV（Qi）is the 1D EP.The DVR method was generalized to deal with chemical physics problems by Light and co-workers［23，25，26］.The present scheme obtained with the PBFC strategy has been shown［3］to be more efficient than the potential optimized DVR scheme［27—29］，since in the latter case the potential itself at specific reference geometries，or slice potential is usually used，which does not contain the information about reaction process.Furthermore，the size of the final Hamiltonian matrix may be reduced using the reduction scheme of Light and co-workers［25，26］.

We illustrate the coordinate grouping pattern by the MA system，in which the 21 normal coordinates are grouped into six collection coordinatesbased on the harmonic frequencies of modes and the specialty of the reaction coordinateQ21.The selection scheme of the collection coordinates may influence the parallel computational efficiency.Numerical tests indicate that it is helpful for the increase of computational efficiency to include those modes of similar frequencies into one combined collection coordinate.Then，the wave function can be expressed as

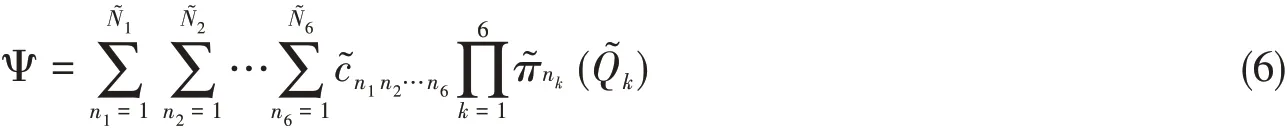
The matrix elements for the final Hamiltonian are，

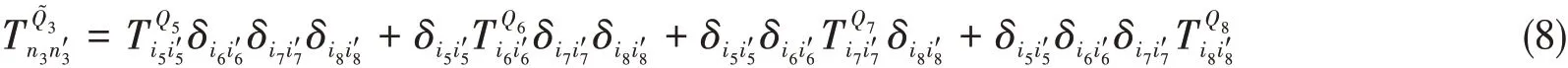
whereT Q j（j=5，6，7，and 8）is the KEM in the DVR forQj.

Fig.6 Schematic diagram of the grouping pattern for the normal coordinates[3]

3.2 Jacobi Coordinate Representation

We take the vinylidene-acetylene（-d2）isomerization syste m as an example，in which the CC-DD Jacobi coordinates［17］（see Fig.4）are chosen.The vibrational Hamiltonian for the nonrotating case has the following form［5］，

whereμi（i=0—2）is the reduced mass；is the angular momentum operator associated withri；andis the vector addition of

To obtain efficient radial DVRs，the 1D effective potentials forr1andr2are customized for the H（D）transfer process.For the angular coordinates（θ1，θ2，φ）andr0，a contraction strategy［30］is applied.

The 4D effective Hamiltonian takes the following form，

wherer1eandr2eare values of the radial coordinates at equilibrium geometry of vinylidene，V4D（r0，θ1，θ2，φ）is the 4D effective potential as described above.The contracted basis functions are obtained with the help of this 4D effective Hamiltonian.

The 4D eigenfunction is expanded in the form of direct product of 1D radial DVR and 3D angular basis functions，

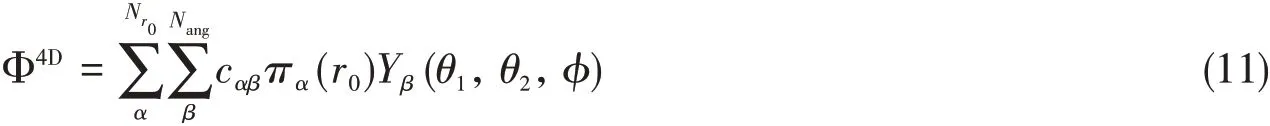
where，πα（r0）is the sine-DVR，andYβ（θ1，θ2，φ）is the normalized uncoupled spherical harmonics functions，

here，Θj1-mandΘj2mare associated Legendre polynomials.To make use of the permutationand paritysymmetries of the system，the primitive angular base can be divided into eight categories［31］.Then ，the total wavefunction is expanded as

3.3 Parallelized Iterative Method

The PI method is used for the solution of the resultant matrix equation，which is helpful to overcome the memory and CPU time bottlenecks in large-scale computations.We utilize the Lanczos method for iteration and the message passing interface（MPI）to parallelize the codes.The Hamiltonian matrix-vector multiplications are very time-consuming in each Lanczos iteration，as a result of which the kinetic and potential energy matrix-vector multiplications are parallelized separately.For the kinetic part，excellent parallel efficiency is achieved for the inner coordinates，since corresponding matrix-vector multiplications are unaffected by the partition of Lanczos vector.However，in the case of the outermost coordinate，the corresponding elements of the Lanczos vector related with the KEM are scattered among all processors，and thus the MPI collection operations are required，leading to the largest communication cost in the whole calculation.In addition，owing to the diagonal potential energy matrix，the matrix-vector multiplication is equivalent to the multiplication of one vector with the Lanczos vector.Since both vectors are partitioned in the same way，the potential energy matrix-vector multiplications can be parallelized without any MPI communication.Using this procedure，only three Lanczos vectors are required to be stored in each iteration，and thus it can be implemented with small memory.

3.4 Combination with the PIST Method

The preconditioned inexact spectral transform（PIST）method is proposed by Carrington and co-workers［32—34］，and we extend the implementation of it to molecular systems with more atoms，combining it into our theoretical scheme for a few applications.The PIST method often uses an optimal separable basis plus Wyatt（OSBW）preconditioner［34—39］，and the resultant scheme is able to solve the eigenvalue problem efficiently.We use MPI to parallelize the time-consuming parts of this scheme，which include the evaluation of Hamiltonian matrix elements，block Jacobi diagonalization and quasi-minimal residual iterations.Furthermore，to acquire a sparse and well-structured matrix，the basis functions need to be separated into the inner and outer groups properly.

4 Other Methods and Applications

4.1 Assignment Method of Vibrational States

To identify the computed eigenstates，we need to analyse the wavefunctions.We propose an easy and effective method，that is，plotting the wave function against relevant normal coordinates.In particular，we transform the wavefunction into a representation as a function of normal coordinates，and then plot it against relevant normal coordinates with the remaining coordinates fixed；according to the nodal structure，a definite assignment could be easily made.For example，we make wavefunction plots［17］（see Fig.7）against the relevant vinylidene normal coordinates and check the nodal structures carefully.Then，from the wavefunction profiles，several important vinylidene states can be definitely assigned.

Fig.7 Wavefunction contour plots of the selected vinylidene-d2 states against the relevant normal mode coordinates(Qi),with the other coordinates fixed at zero[17]

4.2 PES

Since our purpose is to treat both the electrons and the nuclei in a molecular system with quantum mechanical calculations，theab initioPES［40—42］is important，which provides us with the basis for further QD calculations.Manyab initioPESs［18，43—53］have become available，particularly for tri-and tetra-atomic molecular systems.Using these PESs，（ro-）vibrational bound and resonance states can be calculated with the PBFC-PI method.In particular，we performed large-scale parallel calculations for the vinylidene-acetylene（-d2）isomerization on the globalab initioPES developed by Zou and Bowman［30，43］（or the ZB PES），and some results are discussed in the next section.

In recent years，someab initioPESs for polyatomic reactions involving six or more atoms have become available，most of which are dominated by activation barrier［54—59］.To study the H tunneling in MA［3］（see Fig.8），we performed efficient quantum dynamics calculations employing the PES of Wanget al.［54］.In 2016，Qu and Bowman successfully constructed anab initioPES for FAD［55］，and we have performed efficient quantum dynamics calculations of ground-state and fundamental excitation tunneling splittings in FAD using this PES［55］.

4.3 Applications

Using the methods described above，we have investigated the tunneling dynamics of H transfer in important isomerization reactions.Our studied systems include MA，which is a benchmark for the single H transfer［3］（see Fig.8），FAD，which is the smallest prototype for the concerted double H transfer［16］（see Fig.9），and vinylidene-acetylene which exhibits the sequential double H transfer［5］（see Fig.10）.These applications demonstrate the feasibility of our scheme，which may be extended to the study of multiple H transfer dynamics in even larger molecular systems or using more complex models.

Fig.8 Potential energy profile along the isomerization path of malonaldehyde[3]

Fig.9 H transfer along the isomerization path of formic acid dimer[16]

Fig.10 Schematic potential profile of the H transfer path between H2C=C:and:C=CH2[5]

Tunneling splittings can provide direct information about H transfer dynamics and it can be detected by high-resolution spectroscopic techniques［60─63］.As shown in Fig.9，H in FAD can transfer between oxygensviatunneling，resulting in vibrational energy level splitting.Experimentally，Liet al.［62］performed the most accurate measurement ofΔ0of FAD with microwave spectroscopy，and reported a value of 0.01117 cm-1.Based on high resolution spectroscopy，Havenith’s group［64］and Duan’s group［60］measuredΔ0of（HCOOH）2as 0.0158 and 0.01649 cm-1，respectively.In 2017，Duan’group［61］reported an updatedΔ0of 0.011367（92）cm-1for（HCOOH）2.Theoretically，several researchers used approximate methods，such as instanton theory［65，66］and reduced-dimensionality quantum dynamics［55，67］，to study the tunneling splittings.Based on the PES of Bowman’s group［55］，the reduced-dimensional quantum calculations were performed with the multi-mode method［55］and semiclassical calculations were done with the instanton approach by Richardson［66］，however，the agreement with the most recent experiments［61，62］is not satisfactory.

We have performed efficient QD calculations［15，16］on tunneling splittings in FAD，and our computational results are in excellent agreement with the most recent experiments［61，62］.The obtained ground-state tunneling splitting is 0.010 cm-1，whereas the most recent experimental values are around 0.011 cm-1.As for the tunneling splittings upon fundamental excitation and of various deuterium isotopologues，the obtained results are also in very good agreement with experiment.In addition，the mode-specific excitation effects on tunneling rate are systematically revealed and we find that，the remarkable suppression effects upon excitation（see Fig.1）should result from that the anti-symmetric vibrational modes hinder the concerted double H-transfer.The roles of various vibrational modes in the process of H transfer are also studied，and we find that theQ3andQ6are strongly coupled to the H transfer process，withQ3being more important.As shown in Fig.11［16］，the coupling between modes 3 and 1 and that between modes 6 and 1 are very strong，while the coupling between modes 10 and 1 is very small.In addition，the coupling betweenQ1andQ3is anti-symmetric as mentioned in Section 2.1.

Fig.11 PES contour plots(cm-1)for the formic acid dimer along Qi(i=3,6,8,10)and Q1 by fixing the remaining modes at zero[16]

The benchmark vinylidene-acetylene isomerization system has attracted much research attention［5，18，31，68—70］.This system is the simplest one that exhibits the sequential double-H transfer mechanism，and the tunneling splittings［5］can be produced by tunneling between two permutation isomers of vinylidene through the acetylene well（Fig.10）.Previous efforts in search of experimental evidence for acetylene tunneling splittings were not successful［71］.Recently，using the high-resolution cryogenic SEVI method，Neumark and co-workers［18，72］reveal very interesting delicate spectrum structures of vinylidene（-d2），indicating possible tunneling splittings.Several full-dimensional QD calculations of vinylidene（-d2）states have ever been performed by different groups［18，30，31，73—75］，however，the calculational schemes used above have difficulties in dealing with permutation tunneling splittings.

We have performed large-scale parallel calculations［5，17］on theA′1，B′2，A″1andB″2states of vinylidene（-d2），and accurate mode-specific tunneling splittings are reported.As for vinylidene-d2，the largest tunneling splitting we obtain is for the 3ν6state，which has a value of 5.59 cm-1.This value is in reasonable agreement with the splitting width of peak C of cryo-SEVI spectrum in ref.［18］，where Peak C consists of closely spaced doublets and the splitting width is estimated to be 12 cm-1.It is understandable that the tunneling splitting is large for the 3ν6state，since theν6mode［17］（see Fig.12）is the main isomerization coordinate［20，76］in the double H（D）transfer process，and the excitation of theν6mode can enhance the H（D）transfer.However，most obtained tunneling splittings［17］are smaller than 0.3 cm-1.Although the cryo-SEVI spectrum［18］is of much higher resolution than the photoelectron spectrum reported earlier［77］，its resolution is still not enough for such splittings.

Fig.12 Vibrational modes of vinylidene-d2[17]

In addition，our calculated energy levels［17］for both the Franck-Condon（FC）-allowed（A1），and FCforbidden（B2）transitions are in very good agreement with experiment，and the discrepancies between theory and cryo-SEVI experiment［18］are≤30 cm-1for most energy levels.A few deuterated vinylidene states beyond the experimental energy region are reported for the first time.We assign peak C of cryo-SEVI spectrum［18］to the 3ν6state，which is a novel assignment and awaits future verifications.

5 Conclusions and Perspective

The PBFC-PI method，its combination with other methods and the recent progresses in its applications are reviewed.The basic idea of PBFC may have general importance.We have applied this method to study some important issues such as H transfer and tunneling splittings，and our efforts are helpful in extending the time-independent quantum dynamical studies to more complex systems.

Several applications demonstrate the feasibility of above methods，which may be extended to the study of multiple H transfer dynamics in even larger molecular systems or using more complex models.In the future，its applications may even be extended to the study of H tunneling dynamics in important catalytic reactions，such as the reaction catalyzed by an enzyme with the H transfer as the rate-determining step.

More theoretical efforts are required to further increase the parallel computational efficiency of the PBFCPI method，and other coordinate systems such as hyperspherical coordinate will be considered.More high resolution experimental measurements on tunneling splittings are desirable.It is expected that it will become feasible in the near future to treat quantum mechanically both the electrons and the nuclei in a molecular system or a core part of a complex system with more than ten atoms.

This work is supported by the National Natural Science Foundation of China（Nos.21773251，21973098）and the Beijing National Laboratory for Molecular Sciences，China.