低标度XYG3双杂化密度泛函的开发与测评
2021-07-11郑若昕
郑若昕,张 颖,徐 昕
(复旦大学化学系,上海市分子催化和功能材料重点实验室,物质计算科学教育部重点实验室,上海200433)
基于密度泛函理论(DFT)和Kohn-Sham(KS)无相互作用框架下的密度泛函近似方法(DFAs)是目前使用最广泛的第一性原理电子结构计算方法[1].按照Perdew等[2]提出的密度泛函发展途径——雅各布天梯(Jacob’s Ladder),目前常用的DFAs主要隶属于天梯的前4阶近似,仅采用KS占据轨道信息来构造近似泛函[3~25].与之不同,第五阶泛函需引入复杂的KS未占轨道的信息,被认为是最靠近化学精度天堂的最后一阶泛函近似[26~28].
目前最成功的第五阶泛函近似是双杂化泛函(DHA)[26~28].顾名思义,双杂化泛函在采用Hartree-交换形式显式地引入占据轨道信息的同时,更进一步使用二级微扰(Second Order Energy of Perturbation Theory,PT2)相关形式引入未占轨道的信息:
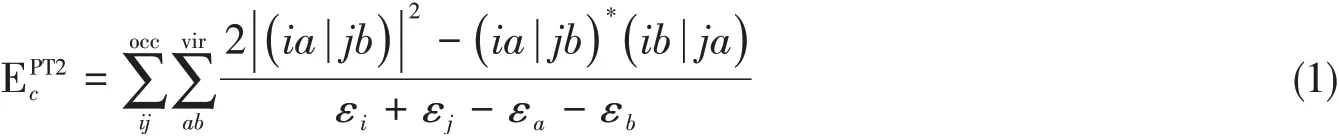

式(1)为闭壳层体系的正则PT2相关能表述形式;开壳层体系的公式相对复杂,但可由式(1)直接推广而得.本课题组于2009年提出了XYG3双杂化泛函[28],具体表达式为
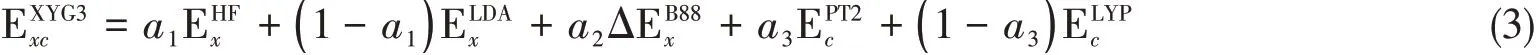

系统的测评和后续应用证明[28~37],XYG3型双杂化方法可非常准确地描述主族元素化学,以二阶微扰波函数方法PT2的计算消耗,接近、甚至达到媲美高等级波函数方法的计算精度.
最近,我们课题组在数值基组框架下的全电子计算软件平台FHI-aims实现了低标度XYG3方法.低标度XYG3方法的程序基础是本文作者之一——张颖博士领衔开发的低标度PT2算法[39,40].PT2的能量计算是基于Hartree-Fock轨道和密度,且包含一份完整的PT2相关能贡献.与之不同,XYG3的能量计算是基于B3LYP轨道和密度,且仅包含32.11%的PT2相关能贡献[见式(4)].将低标度算法应用于XYG3方法,有可能带来不一样的数值收敛表现.本文将简要介绍低标度XYG3方法的基本原理,并开展系统的测评工作.利用一系列水簇体系和ISOL22测试集证明了低标度XYG3可以在保证计算精度的同时有效节约计算时间,减少内存消耗并降低计算标度,对发展适合于上千核并行的低标度双杂化泛函方法,并将其应用于复杂大分子体系有重要意义.
1 公式推导与程序实现
由式(3)可知,XYG3双杂化泛函的计算瓶颈在于PT2部分.低标度PT2的算法推导和具体实现见文献[40].简要来说,低标度XYG3方法继承了Häser等[41]提出的LT-PT2算法,通过拉普拉斯变换,将原本在分母上的特征值转换为指数积分形式[见式(1)],因此亦可称之为LT-XYG3;拉普拉斯变换需数值格点化,以便具体的程序实现.我们的LT-XYG3方法采用了Takatsuka等[42]提出的Minimax Approximation.
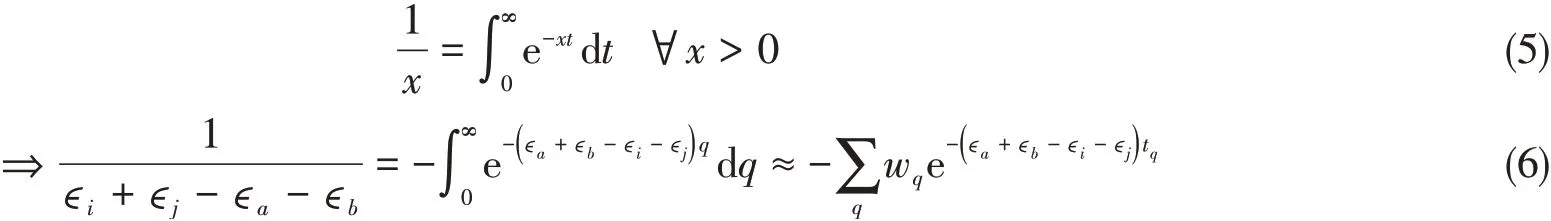
式中:w q和t q分别为Minimax Approximation生成的积分格点q的权重(weight)和根(root).本文将讨论格点积分数量(N q)对低标度XYG3计算结果的影响.由此,正则PT2表述形式[式(1)]中的分子轨道耦合可被分解,从而转化为实空间稀疏的数值原子基表述:

式中:(su|tv)代表原子基函数{φs}的双电子积分:表示占据轨道的伪密度矩阵:




由此,式(7)可进一步简化为
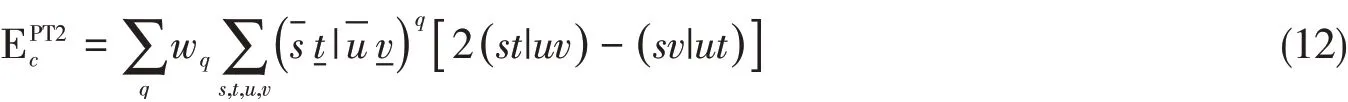
考虑到3类原子基函数{φs,φ-s,φ-t}均有优良的空间局域性,围绕式(12),有望通过引入合适的积分筛选机制以及筛选阈值,开发出兼具高精度和效率的低标度XYG3方法.本工作采用由Ochsenfeld等[43]提出的显式考虑基组对距离的QQZZR4积分筛选策略,讨论不同的积分筛选阈值(θ)对低标度XYG3计算精度的影响.然而式(12)的计算需要准备两类双电子积分增加了相关数据存储和通讯方面的需求以及并行程序实现的复杂度.为应对这一挑战,我们采用局域化的Resolution-of-Identity方案(RI-LVL)[39],将四阶张量的双电子积分(st|uv)近似分解为多个二阶张量的乘积:


式中:P(S,raux)定义了以φs所在原子S为中心、半径为raux的范围内的原子集合.根据这一限制,{φμ}仅包含原子中心落在上述集合内的辅助基函数.系数的确定也是采用直接最小化库仑积分误差的方式(具体推导细节见文献[40]).式(12)~式(14)构筑了低标度XYG3(LT-XYG3)程序的算法基础.本文将讨论辅助基函数构造参数raux对LT-XYG3计算精度的影响.
为了应对积分筛选带来的复杂并行应用场景,LT-XYG3的程序设计跳出“数据分块-计算-通讯”的传统并行模式,而采取了OpenMP[45]与MPI[46]混合并行的框架.图1示出了LT-XYG3中PT2部分的程序伪代码.为了更好地介绍LT-XYG3的程序结构,将式(12)等价变换为
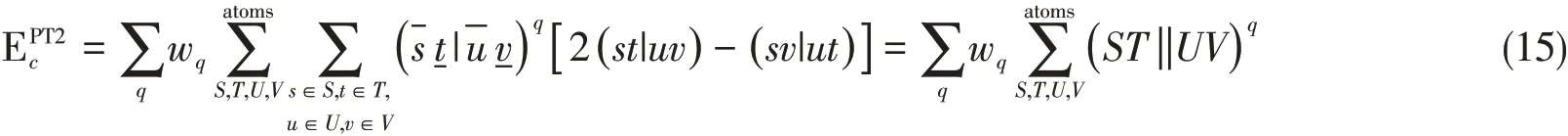
具体来说,我们将计算需求分配到不同的MPI任务中,所有的MPI进程包含在1个或多个计算域(Domain)中,每个计算域中都分配了一整套完整的所需数据,以减少全局的数据交换.而在每个计算域中包含1个或多个对应的MPI进程,每个进程中使用多个OpenMP线程并行,以共享内存的方式减少了线程间的通讯.根据原子序号分组,两组RI系数基函数所在原子S进行分块,并分配至同一个MPI进程中.后续的积分计算在相应的进程中进行线程级并行计算.
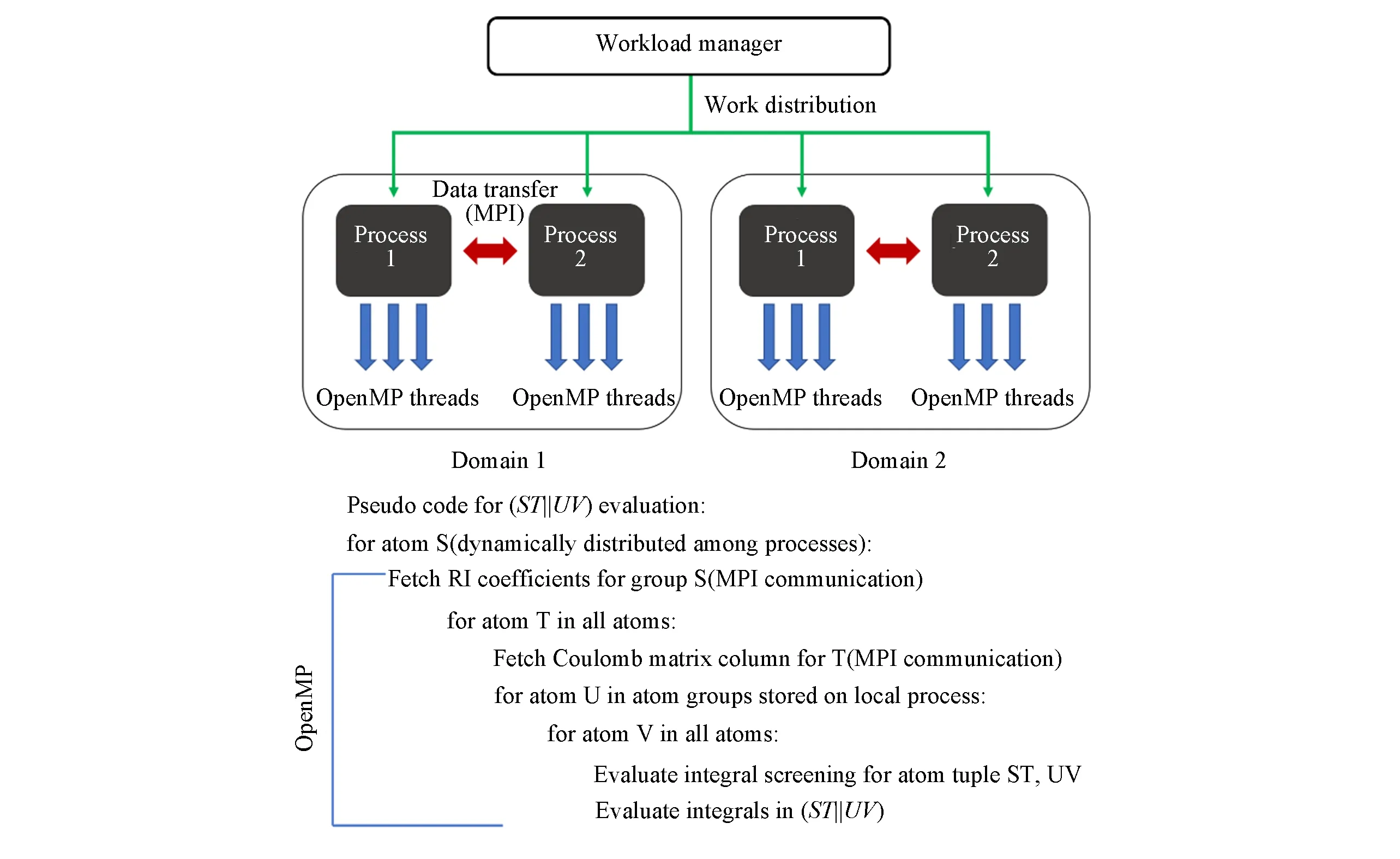
Fig.1 Pseudo code of the OpenMP/MPI hybrid parallel model for the LT-XYG3 method
2 计算细节
低标度LT-XYG3的程序开发在FHI-aims本地开发版本上完成.后续计算采用数值原子基组NAO-VCC-2Z[47].配套的辅助基组采用FHI-aims缺省算法结合NAO-VCC-2Z和额外的1个g函数生成[39,47].所有计算均在课题组自有机群上使用4个32核节点(共128核)完成.具体硬件配置如表1所示.

Table 1 Hardware configuration for calculations
3 结果与讨论
首先研究了拉普拉斯变换积分点的数量N q[见式(6)]、QQZZR4积分筛选阈值θ[见式(12)及相关讨论]以及广义RI-LVL近似下局域辅助基组的选择半径raux[见式(14)]对LT-XYG3计算精度的影响.图2示出了20个水分子团簇计算中LT-XYG3总能量的参数收敛行为;图3示出了LT-XYG3计算中由于低标度算法所带来的近似误差随水簇体系尺寸的变化.我们考察了10~120个不同大小水分子簇[43].所使用的坐标数据由文献[48]中附录得到.
采用标准RI-V近似下的正则XYG3结果为参考标准,仅探讨了LT-XYG3方法中低标度算法引入的上述3个参数的误差收敛行为.由图2不难看出,LT-XYG3的计算结果对筛选阈值比较敏感.为了达到平均每个原子1 meV以下[1 meV/atom,约为0.02 kcal/mol(1 kcal=4186 J)]的计算精度,需要使用θ=10-8或者10-9的积分筛选阈值.与之相反,计算结果对格点积分Nq和辅助基函数选择半径raux收敛很快.Nq=6,raux=6a0(波尔)已经能获得足够精确的LT-XYG3计算结果.
我们随后固定3个参数的设定(raux=6a0,N q=6,θ=10-9),研究了不同大小的水簇体系.由图3可以看出,LT-XYG3的计算精度并没有随着体系尺寸的增大而降低,与基于RI-V的正则XYG3方法相比,误差始终维持在2 meV/atom之内.这表明我们基于局域RI-LVL方法分别生成的原子四中心积分和变换四中心积分在数值上是稳定的.Neese等[49]提出局域相关方法准确性的判据是要包含99.9%的总相关能.本文结果显示,LT-XYG3方法的计算精度已经远低于该判标.
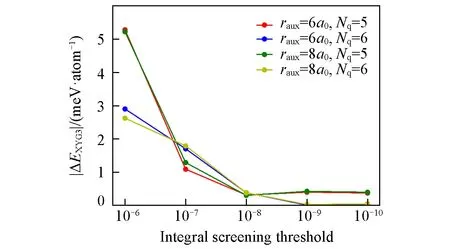
Fig.2 Accuracy of the LT-XYG3 for a water cluster with 20 molecules

Fig.3 Absolute errors per atom in the LT-XYG3 total energies compared with the canonical XYG3 results
图4示出了(LT)-XYG3计算中,与PT2计算瓶颈相关的总时间随体系尺寸变化的趋势.这里考察的计算消耗主要包含RI-V或RI-LVL的系数构建和(LT)-PT2的能量计算所花费的时间.从图4中可以看出,基于局域RI-LVL的LT-XYG3方法展现出了巨大的时间优势.在100个水分子的体系下(这是在所使用的硬件条件下,标准XYG3计算的极限体系),低标度算法LT-XYG3可以带来5倍以上的加速.图4显示,这一加速优势随着体系尺寸的增大将更加明显,展示了LT-XYG3可应用于大体系计算的巨大潜力.
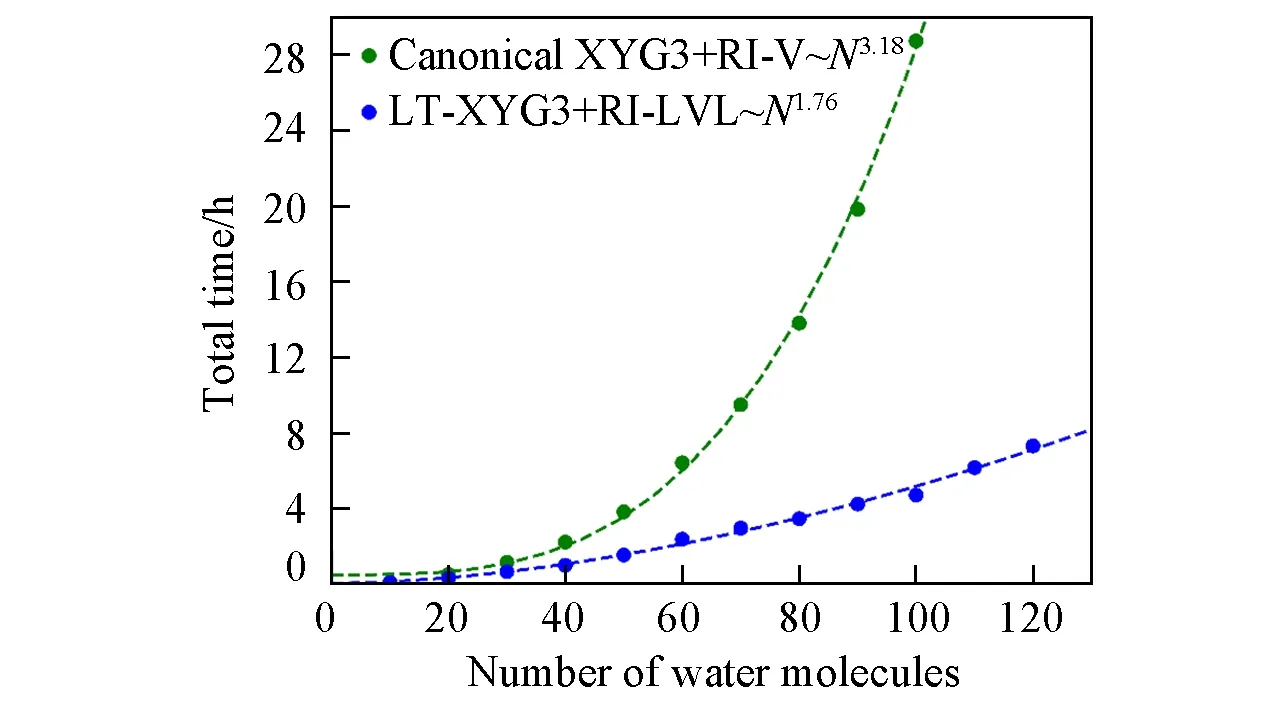
Fig.4 Total time used for the calculation of the XYG3 correlation energy with both the canonical XYG3 and LT-XYG3 implementations

Fig.5 Memory consumption for the generation of RI coefficients in both canonical XYG3(green)and LT-XYG3(blue)
内存消耗同样是电子结构算法开发中值得关注的部分.图5示出了2种方法在最关键的部分,即生成RI系数上的内存消耗.可以看出,基于RI-V方法的标准XYG3计算中,RI系数的内存消耗约是体系尺寸3次方的标度;而基于RI-LVL方法的LT-XYG3由于进一步利用了局域性质,RI系数的内存需求仅为体系的2次方标度.随着体系尺寸的进一步增长,低标度LT-XYG3方法在数据存储上的优势将更加明显.
本文最后一项测试采用ISOL22测试集.该测试集包含22个有机分子异构化反应能[50].所涉及的有机分子尺寸不一,包含24~52个不等的原子数目.以往的测试证明XYG3可以精确地描述此类化学相互作用[50].在NAO-VCC-2Z基组下,我们采用基于标准RI-V方法的XYG3反应能量作为参考值,计算了raux=6a0,N q=6,θ=10-9参数设置下的LT-XYG3结果.表2示出了XYG3与LT-XYG3低标度算法在异构化反应能计算上的数值误差.可以看出,所有的反应能量误差均低于1.7 kJ/mol,而绝对平均误差仅为0.45 kJ/mol.可见,对于重要的化学反应能的描述,引入基于RI-LVL的LT-XYG3低标度近似算法展现出了令人满意的精度.当然,值得注意的是,LT-XYG3的数值误差有一定的系统依赖性,有可能出现LT-XYG3的上述精度表现无法满足特定模拟需求的情况.如表2所示,反应14和16具有非常低的异构化能绝对值.标准XYG3方法给出的异构化能分别为-0.59 kJ/mol和1.85 kJ/mol.LT-XYG3低标度近似引入的误差在反应14上仅有-0.01 kJ/mol(相对误差也仅为1.7%).然而在反应16上,虽然LT-XYG3的绝对误差只有0.86 kJ/mol,但是其相对误差超过了总异构化能的45%.在实际研究中若碰到类似情况,需要通过提高上述介绍的3个与低标度算法精度相关的参数设定来达到更高的精度需求.
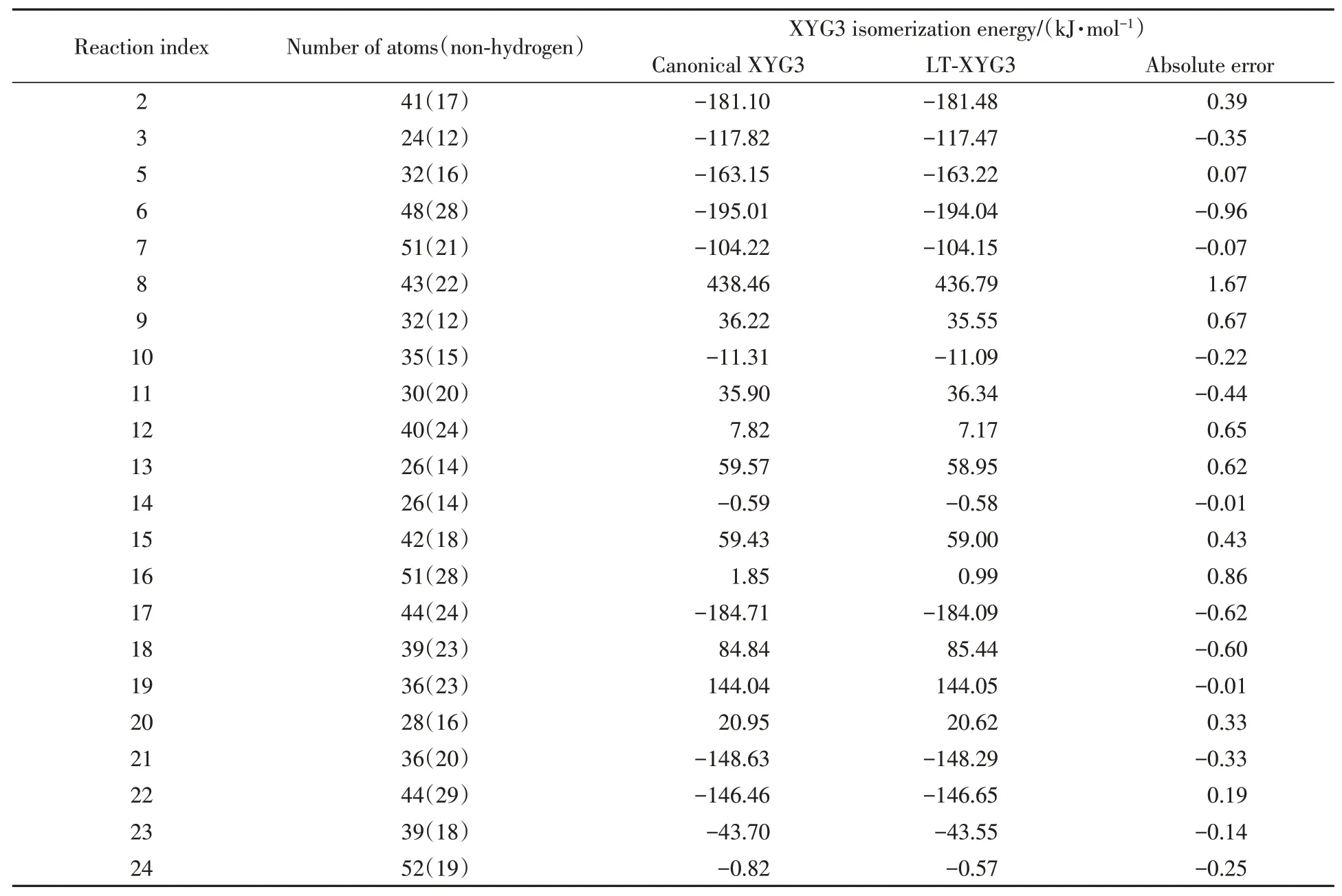
Table 2 XYG3 isomerization energy for the ISOL22 test set
4 结 论
XYG3双杂化密度泛函方法通过引入PT2形式的相关能信息,在计算分子能量性质上表现优秀,然而在计算精度提高的同时也带来了与PT2相当的计算消耗[O(N5)].为了进一步增强双杂化泛函方法的实用性,使其能够应对复杂大体系的研究需求,我们程序化实现了低标度XYG3方法(LT-XYG3),通过结合局域RI方法(RI-LVL)和拉普拉斯变换PT2(LT-PT2)有效降低了双杂化泛函的计算消耗.在该方法中,拉普拉斯变换将PT2的标准离域分子轨道表述转化为更加定域的原子基表述,使得引入积分筛选来降低计算量的低标度算法成为可能.另一方面,我们采用RI-LVL以及辅助基函数的局域性质进一步有效降低了计算需求与内存消耗.然而这一低标度算法也同时带来了不规则的复杂并行应用场景,因此无法通过正常分块的方式对算法做并行处理.LT-XYG3程序采用MPI与OpenMP相结合的混合并行机制,其在被应用于不同尺寸的水簇以及ISOL22测试集的计算时,可以在保持极高的计算精度的同时显著降低内存消耗并提升计算效率,证明了可兼顾高精度和高效率的低标度双杂化泛函方法在有机大分子计算上的可靠性和巨大应用前景.
