从特征值到特征向量以及相关应用
2021-07-09刘国华
刘国华, 许 扬
(1.东南大学 数学学院,南京210000; 2.复旦大学 计算机科学技术学院,上海200433)
1 引 言
设A是复数域上的Hermite矩阵,DENTON P B.,等在文献[3]中证明了A的特征值和特征向量之间满足下面的特征-特征向量等式
其中λ1(A),…,λn(A)是A的特征值全体,∀l∈{1,…,n},νl是A关于λl(A)的特征向量,Ml是A去掉第l行和第l列得到的n-1阶矩阵,λ1(Ml),…,λn-1(Ml),是Ml的特征值全体.此外,(ν1,ν2,…,νn)按列分块做成的n阶方阵是酉矩阵,∀(i,j)∈{1,…,n}2,νi,j表示νi的第j个分量.因此,特征值-特征向量等式反映了A的特征值,Ml(l∈{1,…,n})的特征值,A的特征向量的各分量这三者之间的关系.同时,作者们指出了类似的等式对域上的可对角化矩阵也成立,更一般地,上述等式可以推广到交换环上的可对角化矩阵上.
本文首先证明了交换环上的可上三角化矩阵上的特征值-特征向量等式,所得结果包含了可对角化矩阵的情形,推广了文献[3]的结果.由于域上的任意方阵都可以在基域的代数闭包中上三角化[4],因此本文的结论对域上的任意方阵都成立.在本文的第4节中,给出了特征值-特征向量等式的一个应用,利用交换环上的可上三角化矩阵上的特征值-特征向量等式,证明了对域上的矩阵A的特征值λ,若∀l∈{1,…,n},λ是Ml的特征值,则λ作为A的特征值其重数大于等于2,进一步的,当A可对角化时,前述命题的逆命题也是成立的.
2 一些定义、记号和引理
在本节中,给出文中需要的记号、定义和引理.
给定交换环R,n∈+,用In表示R上的n阶单位矩阵.对R上的n阶方阵A,∀(i,j)∈{1,…,n}2,用A(i,j)表示A的第i行第j列的元素,并记A*是A的伴随矩阵.
下面列出伴随矩阵的若干性质,在[4]中,相应的结论是对数域上的方阵来叙述的,但相同的证明方法和结论对交换环也适用.
命题1设R是交换环,n∈+,A和B是R上的n阶方阵,则
(i)A·A*=A*·A=det(A)I(n);
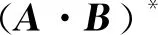
(iii) 若A是上三角矩阵,则A*也是上三角矩阵,并且∀t∈{1,…,n}有
(iv) 若A是对角矩阵,则A*也是对角矩阵;
(v) 若A是R上的n阶可逆矩阵,则det(A) 是R中的乘法可逆元,且
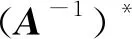
利用命题1,可得下面的推论1,它是下文中主要借助的伴随矩阵的性质.
推论1设R是交换环,n∈+,U是R上的n阶矩阵,P是R上的n阶可逆矩阵,则有

证由命题 1,得到
3 交换环上可上三角化矩阵的特征值-特征向量等式
设R是交换环,n∈,给定P是R上的n阶可逆矩阵,D是R上的n阶上三角矩阵,(c(1),…,c(n))∈Rn,其中
c(i)=D(i,i), ∀i∈{1,…,n}.
(1)
记A=P·D·P-1,∀i∈{1,…,n},B(i)为A去掉第i行及第i列所得的n-1阶方阵.
定理1是本文的一个主要结果,它是文献[2]中特征值-特征向量等式的推广,也可以看作特征值-特征向量等式内容的补充.
定理1取定l∈{1,…,n},则有
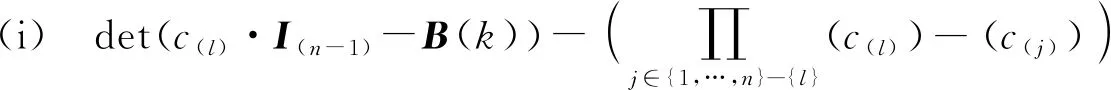

(2)
(3)
证记U=c(l)·I(n)-D,由A=P·D·P-1可得到
c(l)·I(n)-A=P·(c(l)·I(n)-D)·P-1=P·U·P-1.
在上式的两边取伴随矩阵,利用推论1,得到
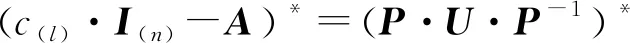
(4)
下面来考察U*,注意到D是上三角矩阵,因此U是上三角矩阵,并且
U(l,l)=c(l)-D(l,l)=c(l)-c(l)=0.
由命题1的(iii)可得U*是上三角矩阵,并且∀i∈{1,…,n}-{l},有
(5)
(6)
另一方面,∀k∈{1,…,n},直接计算可得

(7)
下面证明定理中的两个结论.首先,∀k∈{1,…,n},由(4)和(7)可得

(8)
由U*是上三角矩阵及(5)知
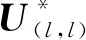
再利用(6)和(8),并注意到U=c(l)·I(n)-D,由上式移项即得(2)对k成立.其次,由(4),(5)和(6)可得
再由(7),即得
结合上面二个等式就证明了(3).
推论2若D是对角矩阵,则∀(l,k)∈{1,…,n}2,
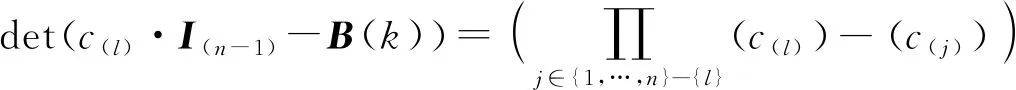
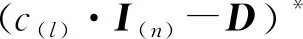

即
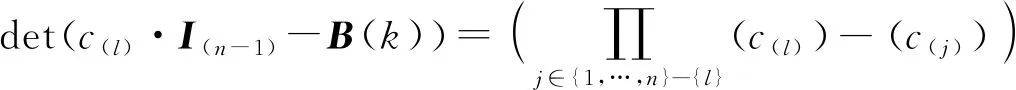
上述推论是域上可对角化矩阵的特征值-特征向量等式在交换环上的推广.当R是域时,由D是对角阵知(c(1),…,c(n))恰是A的特征值全体,再由A·P=P·D可得对∀r∈{1,…,n},P的第r列是A关于c(r)的一个特征向量.最后,∀k∈{1,…,n},设(μ(k,1),…,μ(k,n-1))是B(k)在R的适当扩域中的特征值全体,于是∀(l,k)∈{1,…,n}2,由推论2 可得

上式反映了A的特征值,B(k) 的特征值,A特征向量的各分量之间的关系.进一步的,若R是复数域,A复正规矩阵,并且P是酉矩阵,则上式可写成

即为文献[3]中的特征值-特征向量等式.
4 对域上方阵的一个应用
设F是域,n∈,n≥2,给定A是F上的n阶矩阵,取定λ是A的特征值,记B(i)为A去掉第i行及第i列得到的n-1阶方阵,∀i∈{1,…,n}.
首先,利用第3节的结果来说明,若λ也是B(k)的特征值,则作为A的特征值,λ的重数一定大于等于2.即下面的推论3 和推论4.

证取定F的一个代数闭包k,于是存在k上的可逆矩阵P和上三角矩阵D,满足A=P·D·P-1(文献[1]).因此矩阵D的对角线元素(d(1),…,d(n))是A的特征值全体,又因为λ是A的特征值,故存在(不妨取定)l∈{1,…,n},使得d(l)=λ.对l用定理1的(3),即得
再由k是域,故存在t∈{1,…,n}-{l},使得d(t)=λ.结合d(l)=λ,就得到了作为A的特征值,λ的重数大于等于2.
推论4设∀k∈{1,…,n},λ是B(k)的特征值.则作为A的特征值,λ的重数大于等于2.

下面的推论5说明,当A可对角化时,推论4的逆命题也成立.
推论5设A在F上可对角化,则下面两个命题等价:
(i)作为A的特征值,λ的重数大于等于2;
(ii)∀k∈{1,…,n},λ是B(k)的特征值.
证由推论 4,只需证(i) ⟹ (ii).设有F上的可逆矩阵P和对角矩阵D满足A=P·D·P-1.由(i),存在(不妨取定) (t,r)∈{1,…,n}2,使得
t≠r,d(r)=λ,d(t)=λ,
(9)
∀k∈{1,…,n},对(t,k)用推论2,并注意到d(t)=λ,得到

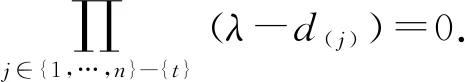
det(λ·I(n-1)-B(k))=0,
即λ是B(k)的特征值.
5 结 论
本文推广了DENTON P B等人关于特征值特征向量的结果,证明了文献中的结果可以推广到域上的可对角化矩阵中的相关等式,更一般地,上述等式可以推广到交换环上的可对角化矩阵上.丰富了线性代数的基础理论.
致谢作者非常感谢《大学数学》的审稿专家,他们的建议使作者受益良多!作者从相关的参考文献中也得到了很多启发,在此表示感谢!
