激光跟踪仪测量回转轴定位精度的误差分析

李 锋，董 浩，王 坚，周兴彪，李高进

（1. 上海外高桥造船有限公司，上海 200137；2. 上海船舶工艺研究所，上海 200032）

0 引言

在多轴数控加工或检测设备的研发、制造和维护过程中，经常会遇到检测直线轴或回转轴定位精度的问题。通常，回转轴的定位精度检测由于受空间布局和测量精度的影响，相对来说适用的测量仪器比较少，检测方案也比直线轴复杂。

激光跟踪仪（Laser Tracker）是一种利用球面坐标定位原理，通过测量1个径向距离和2个角度来实现空间三维坐标测量的高精度检测设备，测量范围可达数十米[1]。由于其灵活便携，安装使用方便，适用范围广，所以激光跟踪仪越来越多地被用来检测数控设备的几何精度或定位精度。然而，激光跟踪仪也有局限性，其2个角度的测量误差相对而言大于径向距离的测量误差，这一特点对回转轴精度测量影响较大。因此，本文对使用激光跟踪仪测量回转轴的误差进行了分析和计算，探讨如何确定检测方案具有足够高的测量精度，避免出现超出预期的测量误差。

1 激光跟踪仪的工作原理和测量误差

1套激光跟踪仪测量系统通常包括1台激光跟踪仪和1个配套的球形反射镜（SMR），以及配套的传感器和电脑等设备。激光跟踪仪内部的主要组成部分有：激光源、2个伺服跟踪旋转轴、光学器件、旋转编码器和环境（气压、湿度等）检测传感器等等。

检测时，SMR放置在目标位置，激光源发射出激光到SMR上，SMR再将光线反射回激光跟踪仪内，通过光学器件和传感器，测出球形反射镜的绝对或相对距离R（绝对距离指球形反射镜到激光跟踪仪原点的距离，相对距离指球形反射镜移动前后两点间的距离）。当球形反射镜的移动方向偏离激光方向时，激光跟踪仪能及时检测到偏离的角度，控制2个伺服旋转轴作出相应旋转动作，使激光的方向始终跟踪对准球形反射镜，避免光路断掉，同时通过2个旋转编码器读出激光的方位角φ和仰角θ。直线激光和2个旋转编码器测出的数据构成1个球面坐标系位置（R,θ,φ），再转换得到目标位置的直角坐标（x,y,z）。

影响激光跟踪仪测量误差的主要因素有：

1）环境因素。大气的温度、压力和相对湿度对光线折射率会产生影响，材料也会因为温度变化产生热变形等，这些因素往往要根据具体的检测环境进行评估，本文不对此进行讨论，文中的分析和计算不考虑温度等环境因素影响。

2）结构因素。由于激光跟踪仪的激光源是安装在2个旋转轴上的，并且在测量过程中会被旋转轴带动旋转，因此旋转轴的机械结构特性如刚性或制造装配误差等，必然会影响到测量结果R的稳定和精确。另外，方位角φ和仰角θ是通过旋转编码器在2个旋转轴上测量出来的，旋转编码器的测量误差也会直接影响到方位角φ和仰角θ的测量精度。

由于角度测量系统（旋转轴和编码器）产生的测量误差比较大，所以用激光跟踪仪时，通常希望各个测量目标点的位置尽量与激光源在一条直线上，以减小旋转角度的测量误差。但是在实际应用中，又往往需要利用激光跟踪仪全方位检测空间坐标点的优势，比如对于检测回转运动，测量的目标点绕回转中心旋转，不可能在一直线上，因此激光跟踪仪在测量过程中必然会发生转动，无法避开角度测量系统的误差影响，这种情况下激光跟踪仪的测量误差会比较大，需要仔细计算评估才能确认是否满足测量目标的精度要求。

根据国家计量标准JJF 1094—2002第5.3.1.4条，测量仪器误差的扩展不确定度U95（置信概率95%）与被测量指标的最大允许误差（绝对值）MPEV应满足以下要求[2]：

式中：U95为95%的置信概率下仪器的测量结果会落在±U95的范围内，U95值越小则测量的结果越可信。在没有实测数据的情况下激光跟踪仪的U95可以根据制造商给出的MPE公式进行评定计算。

激光跟踪仪的最大允许误差不是一个确定的值，通常制造商会给出1组计算公式（以某常用的激光跟踪仪型号为例）。

式中：R为激光跟踪仪到测量目标的直线距离；e为测量的径向误差（沿激光方向），μm；eR0为激光跟踪仪原点到球形反射镜原始位置（TMR）的误差（仪器自身的结构尺寸误差），eR0＝16 μm；eT为测量的横向误差（垂直于激光方向），μm/m。

标准ISO 10360-10的附录E给出了测量2个目标点的间距时最大允许误差的计算方法[3]，根据该算法类推，当测量2个非常接近（几乎重合）的目标点时最大测量误差Emax为：

式中：α数值见图1；O为激光跟踪仪的原点，A是测量目标所在位置，OP垂直于2个测量目标点的连线。α＝∠POA。

图1 夹角α 的几何意义

计算出Emax后，根据均匀分布的方差公式[4]可以得到标准不确定度u为

在实际测量工作中往往还要考虑其它因素产生的不确定度影响，因此需要先计算出这些因素的合成标准不确定度uc后再按下式算出扩展不确定度U95

2 回转轴的精度测量方案和误差分析

由于各种数控设备的回转轴结构差异很大，所以在实际工作中，利用激光跟踪仪检测回转轴精度会有很多种方案，但是这些方案的基本原理大致是一样的。下面以水平转台为例说明测量原理，见图2。

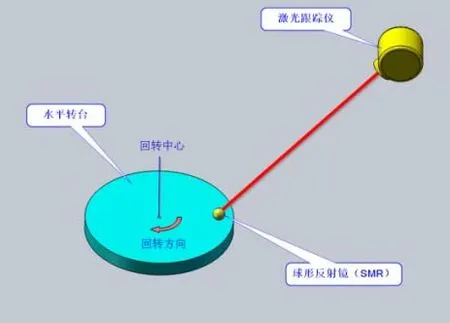
图2 激光跟踪仪测量水平转台示意图

由图2可知，现有一水平转台需要检测回转定位精度，转角的最大允许误差指标MPE＝±0.1°。为检测此精度指标，制定检测方案如下：球形反射镜（SMR）安装固定在转台边缘，激光跟踪仪固定在转台上方；转台从0°开始，每转动一定角度停一下，通过激光跟踪仪读出并记录SMR所在位置的坐标值，全周往复旋转若干次；激光跟踪仪记录的这些坐标点呈圆周分布，用配套软件内置的算法拟合出所有坐标点的旋转圆心，然后就可以得到各个坐标点与初始点（0°）的夹角，算出与目标角度的误差。

激光跟踪仪到回转平面的垂直距离H＝1 000 mm、到回转中心轴的垂直距离L＝1 500 mm。球形反射镜（SMR）固定安装在转台靠近边缘的A点位置，A到转台回转中心C的距离（即回转半径）r＝200 mm。转台从零度开始旋转，每间隔45°检测1次SMR的坐标，转到360°时改变回转方向，如此全周往复回转3个循环，每个循环有正向和反向各8个坐标数据，根据测量到的坐标数据用软件拟合出回转中心并计算各测量点坐标对应的回转角度及偏差。

该方案的测量不确定度计算如下：假定检测过程中环境温度变化很小，可忽略温度变化导致的不确定度，下面只考虑激光跟踪仪的测量误差导致的不确定度。已知回转角度θ（单位：弧度）、回转半径r和SMR经过的弧长s符合以下关系：

式中：us和ur分别是SMR回转圆周切向和径向2个正交方向上的测量标准不确定度。图3是转台回转角度θ＝45°时（SMR位于A1位置）的简图。

图3 转台回转角度θ＝45°时，SMR 与激光跟踪仪原点的几何关系

Ai（i＝0～7）是转台回转1周范围内SMR所在的8个检测位置，CAi＝r＝200 mm。O是激光跟踪仪的原点，O到回转平面的投影点为B，OB＝H＝1 000 mm。B到回转中心C的距离BC＝L＝1 500 mm。

图3(a)中PA1是圆的切线且OP⊥PA1，图3(b)中CQ过A1点和圆心C且OQ⊥CQ。只要计算出激光跟踪仪原点O到检测位置A1的距离R、∠POA1的角度α、∠QOA1的角度β，再根据公式（2）～式（5），便可算出激光跟踪仪测量误差在A1位置的切向标准不确定度us和径向标准不确定度ur。其它各Ai点位置均可按此方法计算。

根据几何关系推导可得出：

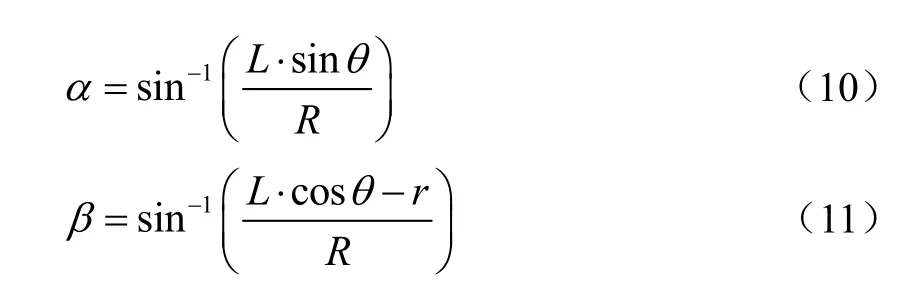
计算各检测位置对应回转角度的合成标准不确定度如表1所示（由于点A5～A7与点A3～A1对称，计算结果相同，故表1中不列出）。

表1 各回转角度的合成标准不确定度计算表

表1中，e、eT为激光跟踪仪自身的径向和横向测量误差，由式（2）、式（4）计算可得；Esmax、Ermax为测量圆周上各检测点的最大误差（s为切向、r为径向），由式（5）计算（计算径向最大误差Ermax时，用β代替公式中的α）可得；us、ur为测量圆周上各检测点的标准不确定度（s为切向、r为径向），由式（6）计算（切向和径向分别用对应的最大误差Esmax、Ermax计算）可得；uc为测量回转角度的合成标准不确定度（切向us与径向ur的合成），由式（9）计算可得。

由表1可知，最大的合成标准不确定度出现在A4位置，即转台转角180°的时候，根据式（7）计算出此时的扩展不确定度U95＝0.034 4°。

由于此设备的误差指标MPEV＝0.1°，而测量方案的U95略大于MPEV的1/3，不满足式（1）的要求，说明测量结果可信度偏低，需要调整测量方案。根据前述计算分析可知，调整SMR到回转中心的半径r，且激光跟踪仪相对于转台的位置H和L3个参数可以有效合理地降低测量的不确定度。

3 结论

激光跟踪仪使用灵活方便，测量范围大，广泛地用于各种直线轴和旋转轴定位精度的测量工作中，但是由于其角度测量误差较大，如果不进行误差分析，很可能会因为测量误差太大导致最后测出的结果不可信。

因此，在制定测量方案时，需要根据激光跟踪仪、球形反射镜与回转轴的相对几何位置关系，计算出激光跟踪仪在不同方向上的最大测量误差，再据此算出回转角度测量的不确定度U95并与检测指标MPEV进行比较，如果不满足U95≤MPEV/3，则应调整测量方案，改变激光跟踪仪或球形反射镜的位置，再重新进行误差分析和不确定度评定，直到满足检测指标的精度要求。

本文给出的误差分析和不确定度评定方法，虽然是以水平转台为例，但是对于其它方向的回转轴定位精度检测也具有参考价值，应用时需要根据不同的运动转轴方向和差异化的机械空间结构进行有针对性的调整。