也谈洛伦兹力公式中速度的参考系选择问题

周 凯

(深圳实验学校光明部,广东 深圳 518107)

参考系是物理学中的重要概念,我们在研究物理问题时,首先要选定参考系.然而,在高中物理电磁学的教学中,关于洛伦兹力公式及由洛伦兹力产生的动生电动势公式中的速度是相对于哪个参考系而言的这一问题,文献中仍持有不同观点.[1-2]文献[1]认为洛伦兹力公式中的速度是电荷相对于观察者的速度,而文献[2]认为洛伦兹力公式和动生电动势公式中的速度都是电荷(导体)相对于磁场的速度.本文就结合以下2个例题,谈谈对此问题的看法.

1 从电磁场的相对论变换角度看动生电动势

例1.(2021届广东省高三“6校联盟”第3次联考)如图1所示,是某学生设计的一种磁动力电梯的原理图,即在竖直平面内有两根很长的平行竖直金属轨道MN和PQ,轨道间有垂直轨道平面的匀强磁场,两导轨下端用导线相连.处于金属轨道间的导体杆ab与轨道垂直,且下方通过绝缘装置固定电梯轿厢,当磁场向上运动时,电梯可向上运动(设运动过程中ab始终与导轨垂直且接触良好).已知匀强磁场强度为B,电梯载人时电梯轿厢及ab杆的总质量为M,两导轨间的距离为L,导体杆电阻为R,其余部分电阻不计.当磁场以v0的速度匀速上升时,电梯轿厢刚好能离开地面.不计空气阻力,ab杆与轨道的最大静摩擦力大小与滑动摩擦力大小相等.重力加速度为g.求:

(1) 此时通过ab杆电流的方向及ab杆受到轨道的摩擦力的大小；

(2) 当电梯匀速上升的速度大小为v1时,磁场向上匀速运动速度v2的大小.

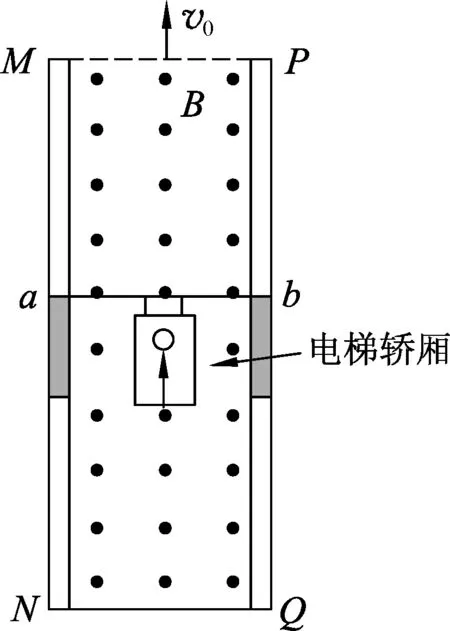
图1 磁动力电梯原理图

参考答案如下.

(1) 由右手定则可得电流方向是b→a,磁场向上运动,相当于ab杆向下切割磁感线,

电梯轿厢刚好能离开地面,可得

F安1=Mg+f，

可得

(2) 当磁场向上匀速运动速度v2时,回路中感应电动势的大小

E1=BL(v2-v1)，

稳定时,对电梯轿厢受力分析有

F安2=BI1L，

F安2=Mg+f，

可得

v2=v0+v1.

参考答案中认为“磁场向上运动,相当于ab杆向下切割磁感线”,这一解法看似合理,实际上是将导体切割磁感线的速度理解为导体相对于磁场的速度.许多教师在教学中也会特别强调:动生电动势公式中的速度是导体相对于磁场的速度.由于大多数题目中磁场都是静止的,因此导体相对于磁场的速度等于导体(相对于实验室参考系)的速度.动生电动势的中的非静电力是洛伦兹力,对于洛伦兹力公式中的速度,也有与上面相似的理解.

然而,站在电动力学的角度看,运动的磁场会产生电场,在电磁场中运动的粒子会受到洛伦兹力的作用,洛伦兹力公式为F=qE+qu×B.其中等号右边第1项电场力,第2项是磁场力(即高中物理中所学的洛伦兹力).电磁场的相对论变换告诉我们,电磁场作为客观存在的物质场是统一的不可分割的整体,在某一惯性系中可以把它分解成这样的电场和磁场两部分,在另一个惯性系中又可以把它分解成那样的电场和磁场两部分.[3]因此,洛伦兹力公式中的电场E、磁场B、速度u必须是相对于同一惯性参考系而言的.在不同参考系中看,特别是在高速运动的情况下,粒子在电磁场中所受力的值甚至都是不同的.这样动生电动势中非静电力的情况也是不同的.我们有必要借助电磁场的相对论变换有关知识来分析一下,相对于不同的参考系例题1第2问中导体棒中电荷的受力情况,并对比在不同参考系下本题的物理图像.

如图2所示,有两个惯性参考系,∑系静止,即我们通常所说的实验室参考系,∑′系相对∑系以速度v2向上匀速运动.选∑′系固定在磁场上,磁感应强度方向沿z′轴正方向.位于∑′系中的观察者认为,这个磁场是静止的,其周围空间只存在静磁场,电场强度和磁感应强度分别为

Ex′=0，Ey′=0，Ez′=0，

Bx′=0，By′=0，Bz′=B.

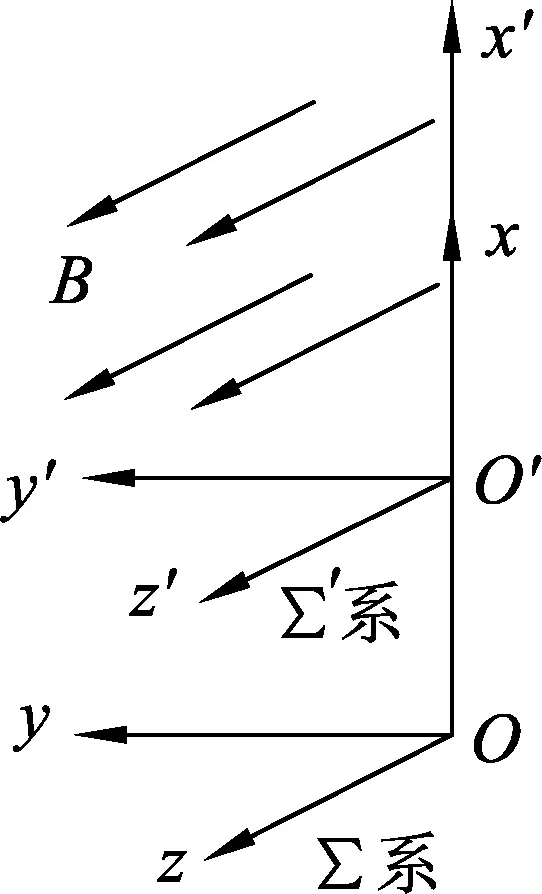
图2 ∑、∑′两惯性系之间的变换

由电磁场的洛伦兹变换公式得,在∑系中的电场强度和磁感应强度分别为

Ex=Ex′，Ey=γ(Ey′+v2Bz′)，

Ez=γ(Ez′-v2By′)；

式中

(1)

以上可以看出,不同参考系中的电场和磁场不是分开来各自进行变换的,而是相互联系在一起变换的,它们可以相互转化.电场和磁场是电磁场统一体的不同方面,电场和磁场的6个分量联合起来描述电磁场的性质.[4]

在非相对论近似下,即v2≪c,由(1)式得γ=1,这样过渡到非相对论电磁场变换公式

Ex=0，Ey=v2B，Ez=0；

Bx=0，By=0，Bz=B.

即在∑系中的观察者认为,空间同时存在沿y轴正方向的电场Ey=v2B和沿着z轴正方向的磁场Bz=B.

再看两个参考系中导体杆ab的速度.在∑系中,导体杆的速度为

ux=v1，uy=0，uz=0.

由相对论速度变换式可得在∑′系中,导体杆的速度为

可见,在非相对论近似下,速度的变换关系回到我们熟悉的伽利略变换

ux′=v1-v2，uy′=0，uz′=0.

下面我们求解动生电动势,在∑系中,导体杆中的正电荷受到的非静电力可分成两部分,第1部分为沿y轴正方向的电场力,第2部分为沿y轴负方向的磁场力.作用在单位正电荷上的非静电力(洛伦兹力)为

K=Eyj+uxi×Bzk=(v2-v1)B j，

(2)

其中i、j、k分别是x轴、y轴、z轴正方向的单位矢量.动生电动势为

(3)

在∑′系中,导体杆中的正电荷受到的非静电力为沿y′轴正方向的磁场力,作用在单位正电上的非静电力(洛伦兹力)为

K′=ux′i′×Bz′k′=(v2-v1)B j′，

(4)

其中i′、j′、k′分别是x′轴、y′轴、z′轴正方向的单位矢量.动生电动势为

(5)

这里由于我们忽略了相对论效应,因此(3)式和(5)式中导体杆的长度L相同.

对比(3)式和(5)式的结果,我们发现在两个参考系中算出的动生电动势的值是相同的.但仔细分析以上过程,我们会发现相对不同参考系对问题理解的差异.①两个参考系中的观察者观测到的场的情况不同:∑系(实验室参考系)中的观察者观测到的是电磁场；而在∑′系(固定在磁场上的参考系)中的观察者观测到的是静磁场.②非静电力的性质不同:∑系中导体杆中电荷受到的非静电力为电场力和磁场力之和(电动力学中的洛伦兹力),而∑′系中导体杆中电荷受到的非静电力仅为磁场力(高中物理所学的洛伦兹力).③我们是在非相对论近似下得到∑系中电磁场以及导体杆在∑′系中的速度的,这样求出的洛伦兹力(2)式和(4)式的结果是相同.若考虑相对论效应,力的洛伦兹变换为

可见,在非相对论近似下,上式可化简为

Fx′=Fx，Fy′=Fy，Fz′=Fz.

即在低速的情况下,不同惯性系中的作用力是不变的.正因为这一点,在∑系和∑′系中洛伦兹力是相等的,在不考虑长度收缩效应时,我们计算出的动生电动势的值是相等的.值得注意的是,我们这里所说的洛伦兹力,必须是电动力学中包含电场力和磁场力在内的完整的洛伦兹力.

从上面的讨论可以看出,由于高中物理知识的局限性,实际上,多数教师并没有考虑到由于磁场运动而引起的空间产生电磁场这一效应,在处理磁场相对实验室参考系运动时的电磁感应问题时,习惯性地选择了以磁场为参考系(准确地说是选择了固定在磁场上的参考系).因此,在动生电动势的教学过程中,多数教师会强调公式BLv中的速度指的是导体相对于磁场的速度.这样在处理导体不动,磁场运动的问题时,才可以使用高中物理知识进行解题.而在求出电动势之后,进而求出安培力,对物体进行受力分析时,又转入到实验室参考系下进行研究,这样求出物体的加速度、速度、轨迹就是都是相对于实验室参考系的.这样的过程看似合理,而实际上是在解题过程中更换了参考系,学生甚至部分教师通常是没有意识到这一点的.

2 带电粒子在运动磁场中的轨迹问题

在高中阶段,我们在学习带电粒子在匀强磁场中的偏转时,题目中磁场通常是静止的,这样无论相对于实验室参考系还是相对于固定在磁场上的参考系,粒子都做圆周运动.如果在粒子运动的同时,磁场也在运动,那么相对于实验室参考系和固定在磁场上的参考系,粒子的轨迹各是怎样的？下面我们就运用电磁场变换的有关知识,研究一下不同参考系中粒子的受力情况和运动轨迹.

例2.如图3所示,半无界匀强磁场的磁感应强度B沿z轴正方向,t=0时刻一带电粒子(电荷量q>0)以速度v1沿着x轴正方向射入磁场,同时磁场以速度v2(v1>v2)沿着x轴正方向运动.求带电粒子的轨迹.

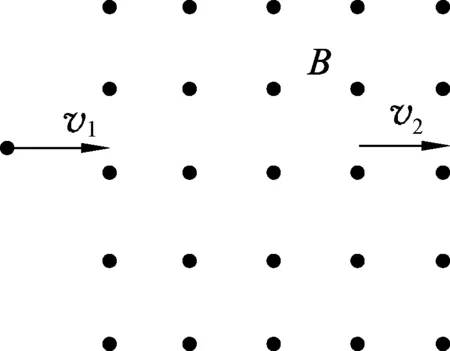
图3 带电粒子在运动磁场中的运动

由上面关于例1的讨论可知,在不同的参考系中,电磁场的各分量是不同的,粒子的受力情况也不同的,我们必须明确所求的轨迹是相对于哪个参考系而言的.

令K和K′是两个惯性系,取直角坐标系Oxyz和O′x′y′z′,相应坐标轴平行.K′系相对于K系以速度v2沿x轴正方向作匀速运动.在t=0时刻原点O和O′重合.K′系中的电磁场分量为

Ex′=0，Ey′=0，Ez′=0，

Bx′=0，By′=0，Bz′=B.

粒子在K′系中的速度为

ux′=ux-v2，uy′=uy，uz′=uz.

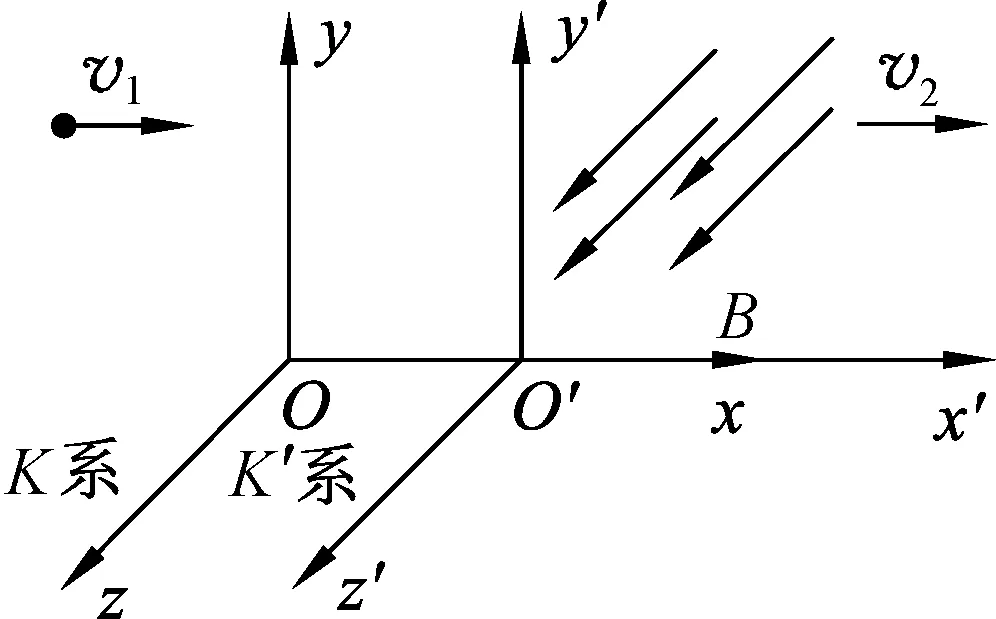
图4 带电粒子在运动磁场中的相对论分析

粒子所受的作用力只有磁场力

则粒子运动的微分方程为

(6)

(7)

对(6)式微分,得

(8)

将(8)式代入(7)式,得

(9)

微分方程(9)式的通解为

同理可得

当t=0时,ux′=v1-v2,uy′=0,解得φ=0,A=v1-v2.

(10)

(11)

对(10)式积分可得粒子相对于K′系的运动轨迹

(12)

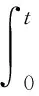
(13)

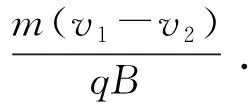
根据非相对论电磁场变换公式,我们可以得到K系中的电磁场分量

Ex=0，Ey=v2B，Ez=0；

Bx=0，By=0，Bz=B.

即在K系(实验室参考系)中,空间存在沿着y轴正方向的电场Ey=v2B和沿着z轴正方向的磁场Bz=B.粒子所受洛伦兹力为

粒子运动的微分方程为

仿照上面的解法同理可得粒子在K系中的速度和轨迹

可以看出,粒子的运动为匀速圆周运动和沿x轴正方向的平动的合成,其轨迹为摆线.[5]

当然我们也可以从相对运动角度考虑这个问题,在K系中看粒子做圆周运动,而在非相对论近似下,坐标的洛伦兹变换将回到伽利略变换.粒子在K系中的运动即为粒子相对K′系中运动和磁场的运动的矢量和.

3 总结

本文运用电磁场相对论变换的有关知识,对高中物理中运动磁场中导体产生动生电动势的本质进行了研究,对洛伦兹力公式以及动生电动势公式中的速度是相对于哪一参考系而言的这一问题，给出了较为清楚的解释.公式中的速度、电场、磁场都是相对于同一个参考系而言的,即都是相对于观察者而言的.当磁场运动时,空间中会激发电磁场,我们只有采用电动力学中完整的洛伦兹力公式才能得到正确的动生电动势的结果.虽然在非相对论近似下,在不同的惯性参考系中,洛伦兹力的数值是相同的,但实际上不同参考系中观察到的电磁场的情况是不同的.我们还求解了带电粒子在运动磁场中的轨迹问题,本文的研究结果有助于中学物理教师加深对电磁场统一体的认识和对运动磁场中电磁感应问题物理图像的理解.