一个扰动的Ostrowski型不等式的加强

时统业

（海军指挥学院，江苏 南京 211800）

1 引言与预备知识

在文献[1]中，Ostrowski建立了下面的积分不等式：

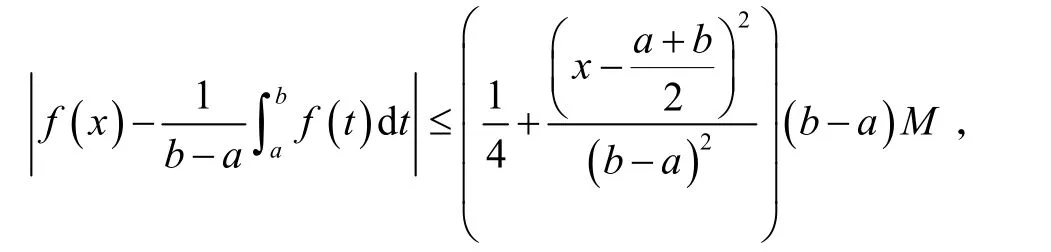
其中f:［a,b］→R在［a,b］上连续，在 （a,b）上可微且f'有界，即

文献[2]证明了当f:［a,b］→R在 ［a,b］上满足M-Lipschitz条件时（即对任意t1,t2∈［a,b］有则Ostrowski不等式也成立.

针对二阶导数有界的二次可微函数，文献[3]建立了下面的带有扰动的Ostrowski型不等式：

其中f: ［a,b］→R二次可微，且f''在（a,b）上有界，即

有关二阶可微函数的Ostrowski型不等式的内容还可参见文献[4-9].本文仿照文献[10]引入参数求最值的方法，给出式(1)的加强.我们需要的引理1从文献[3]或[6]的定理证明过程可以得到.

引理1设f: ［a,b］→R在 （a,b）上二次可微，且f''在［a,b］上可积，则对任意x∈［a,b］有：

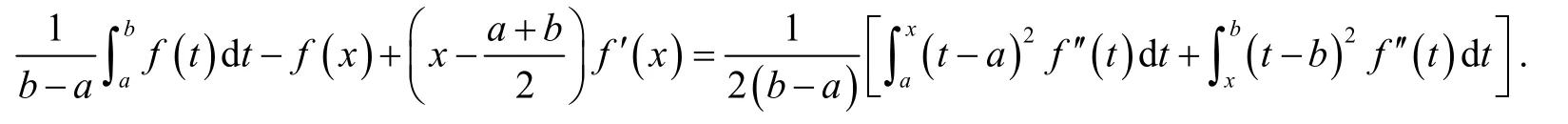
2 主要结果

定理1设f: ［a,b］→R在（a,b）上二次可微，且f''在［a,b］上可积，存在常数m和M，使得对于任意t∈ （a,b）都有m≤f''（t）≤M，则对任意x∈［a,b］有：

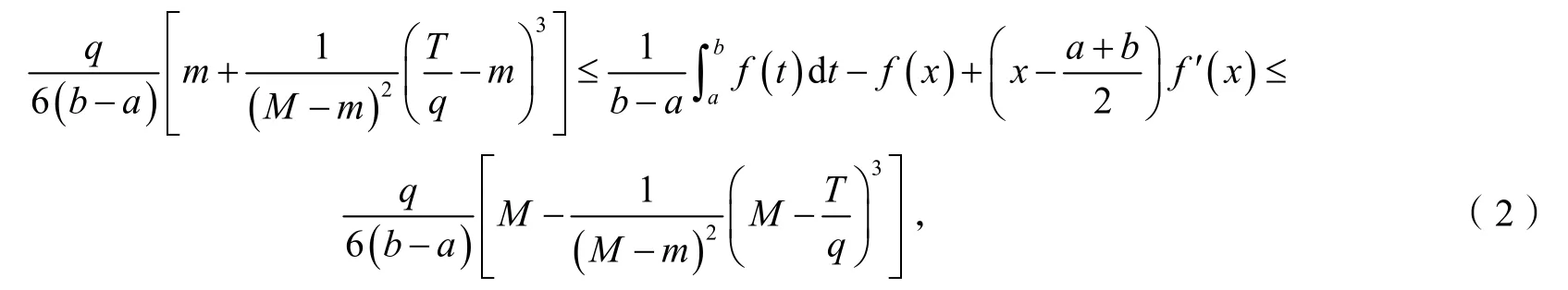
证明先考虑x=a的情形.由引理1有：

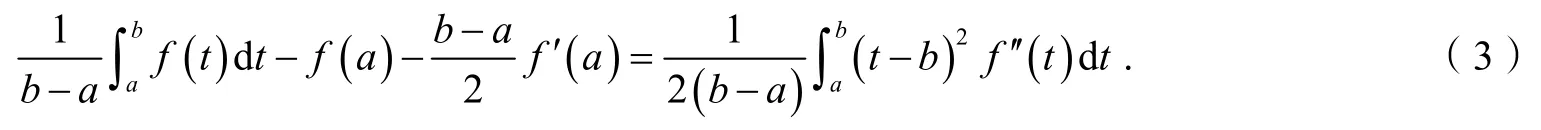
对任意常数ε∈ ［ 0,b-a］，当t∈ ［a,b-ε］时有 （t-b）2-ε2≥ 0 ；当t∈ ［b-ε,b］时有 （t-b）2-ε2≤0.利用式（3）有：

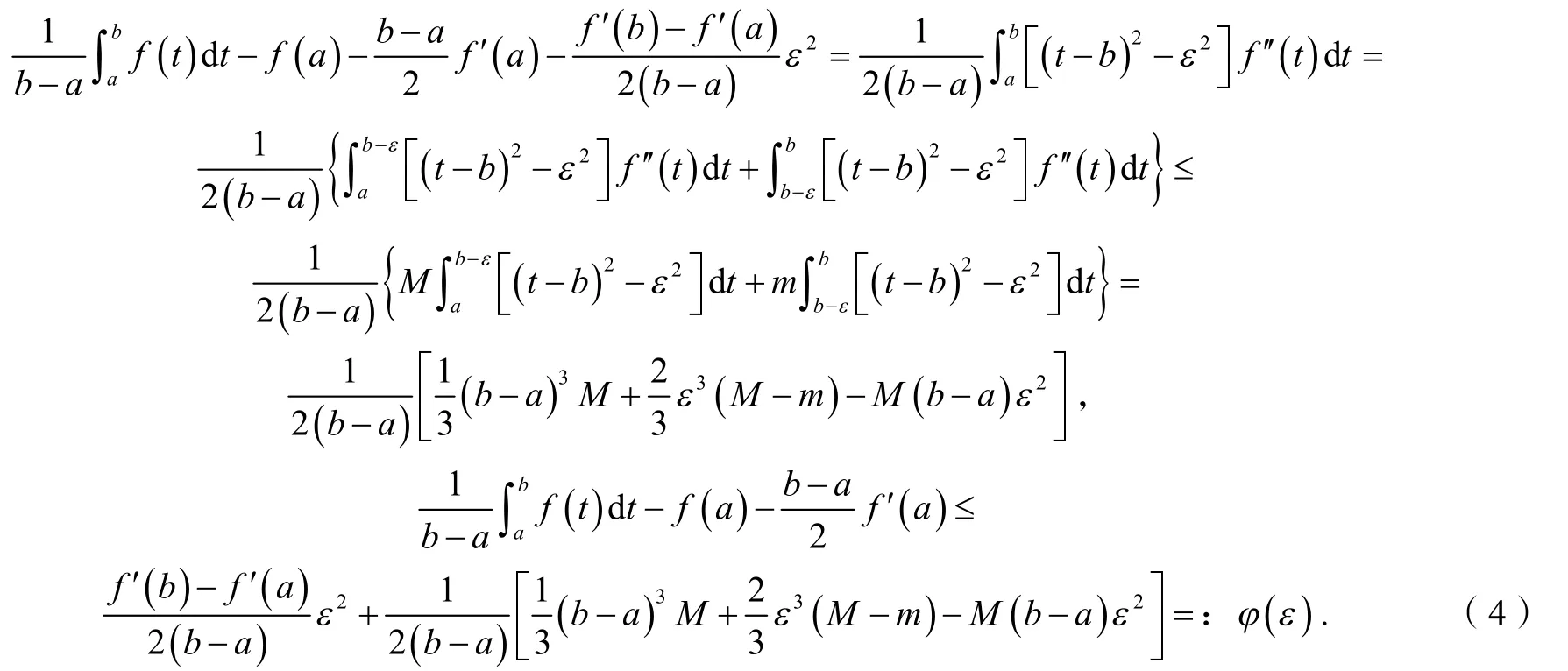
为求φ（ε）的最小值，求导得当ε∈ ［ 0,ε1］时φ'（ε）≤0，当ε∈［ε1,b-a］时φ'（ε） ≥ 0，故φ（ε）在ε=ε1时取得最小值.在式（4）中取ε=ε1，得：

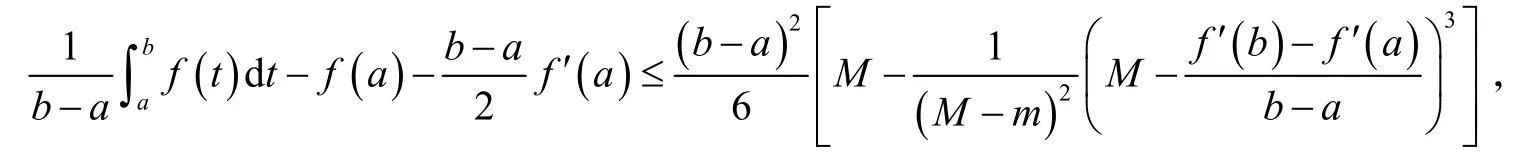
即当x=a时式（2）的右边不等式成立.接下来考虑x∈（a,b］的情形.

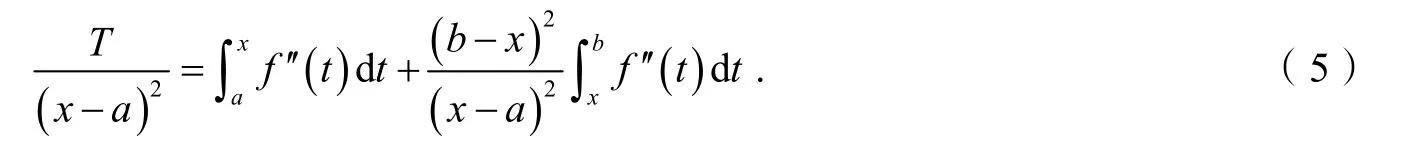
对 任 意 常 数ε∈ ［ 0,x-a］，当t∈ ［a,a+ε］时 （t-a）2-ε2≤0 ； 当t∈ ［a+ε,x］时 （t-a）2-ε2≥ 0 ； 当时 （t-a）2-ε2≤0.利用引理 1和式（5）得：

为求φ（ε）的最小值，求导得

由式（5）得T∈ ［mq,Mq］，故ε2∈ ［ 0,x-a］，且φ（ε）在ε=ε2时取得最小值.在式（6）中取ε=ε2，证得：当x∈（a,b］时式（2）的右边不等式成立.当m≤f''≤M时有-M≤（-f）″≤-m，对-f应用已证明的结果，则式（2）的左边不等式得证.

推论1设条件同定理1，则对任意x∈［a,b］有：

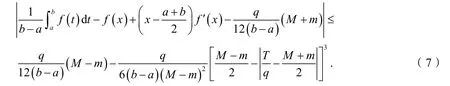
证明如果A1+B1≤I≤A2-B2(B1≥ 0,B2≥0)，则有A1+min ｛B1,B2｝≤I≤A2-m in ｛B1,B2｝，从而有利用这个事实，由定理1则推论得证.

推论2设条件同定理1，则有：

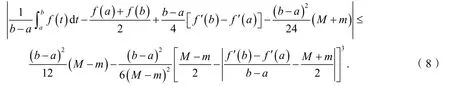
证明在推论1中分别取x=a和x=b得：

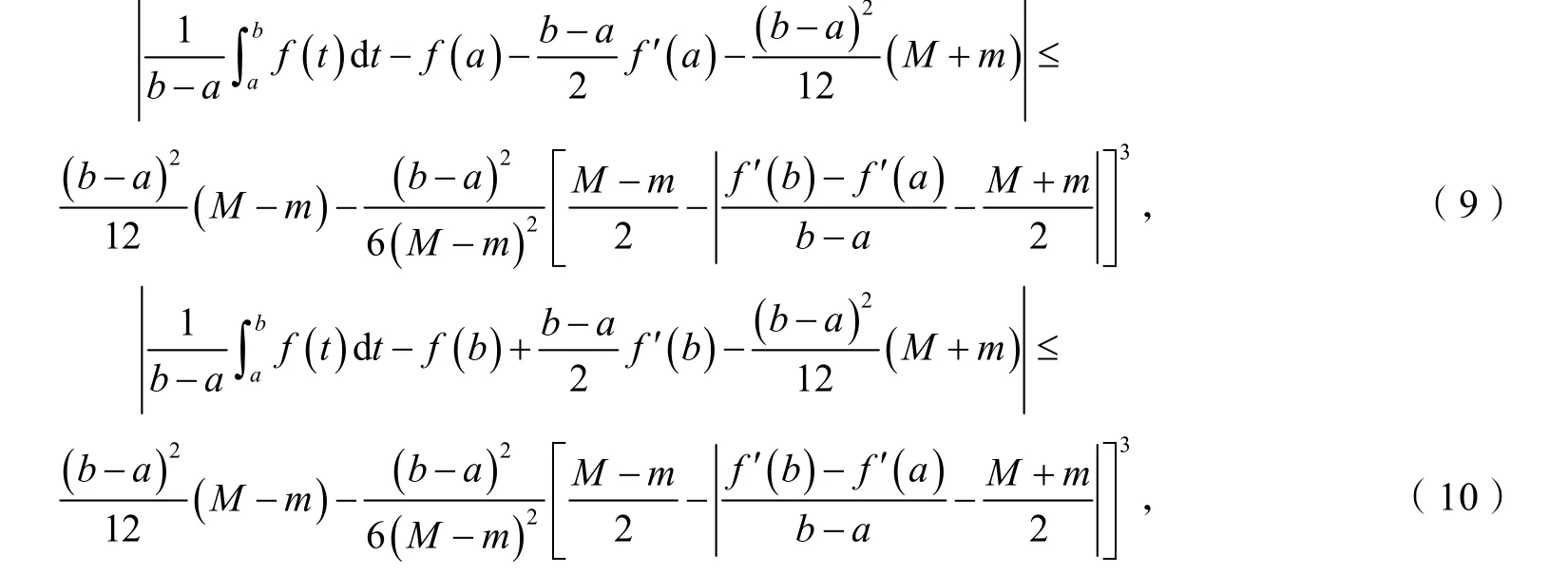
将式（9）和式（10）相加，并利用三角不等式，则式（8）得证.

注1当时，式（8）的估计优于经典梯形不等式

推论3设f: ［a,b］→R在（a,b）上二次可微，且f''在［a,b］上可积，存在常数M，使得对于任意则对任意x∈［a,b］有：

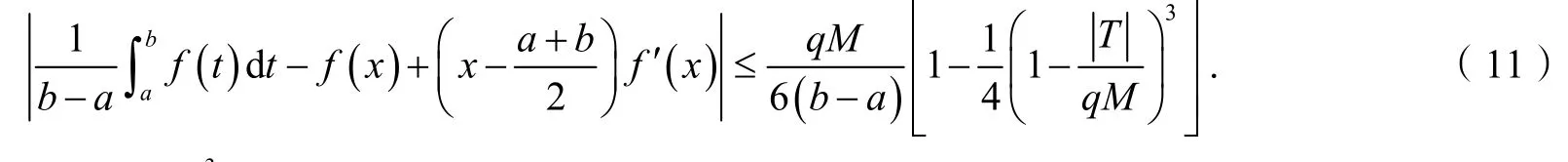
注2注意到因此式（11）给出了式（1）的加强.

推论4设f: ［a,b］→R在（a,b）上二次可微，且f''在［a,b］上可积，存在常数M，使得对于任意t∈ （a,b）都有则有：

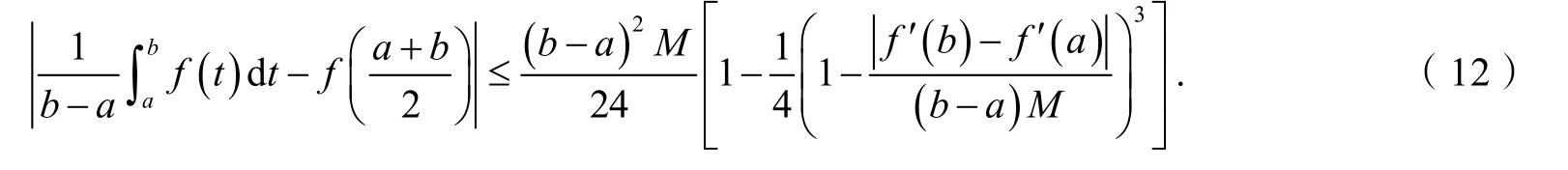
证明在推论1中取则式（12）得证.

注3式（12）是经典的中点不等式的加强.

定理2设f: ［a,b］→R是可微函数，且f'满足（m,M）-Lipschitz条件，即存在常数m和M，使得对于任意s,t∈ ［a,b］,s＜t，有m（t-s）≤f'（t）-f'（s）≤M（t-s），则有式（2）成立.

证明当x=a时，对任意常数ε∈ ［ 0,b-a］，有：

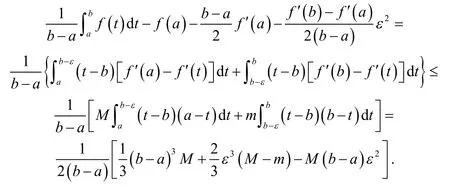
当x∈（a,b］时，对任意常数ε∈ ［ 0,x-a］，有：

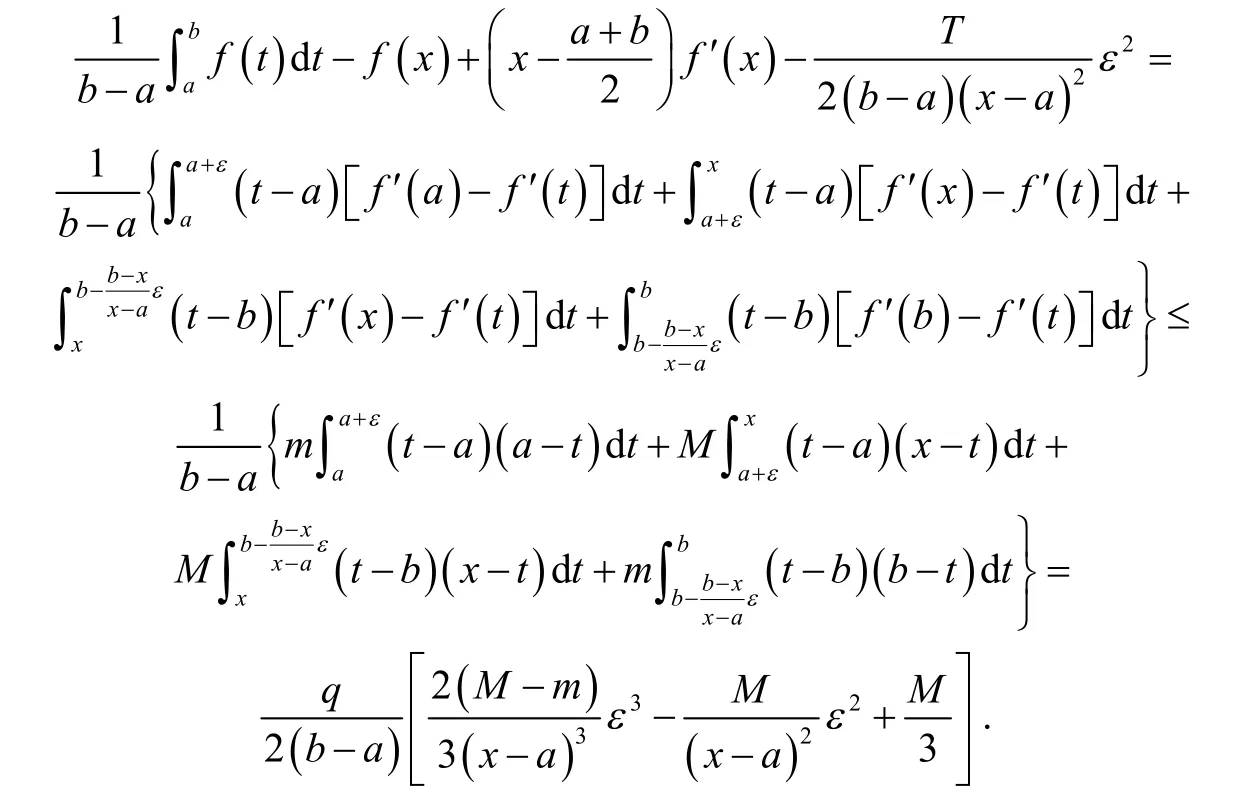
接下来的证明类似于定理1，这里略去.

推论5设条件同定理2，则任意x∈［a,b］有式（7）成立.

推论6设f: ［a,b］→R是可微函数，且f'满足M-Lipschitz条件，即存在常数M，使得对于任意s,t∈ ［a,b］,s＜t，有则对任意x∈［a,b］有式（11）成立.

推论7设f: ［a,b］→R是可微函数，且f'满足M-Lipschitz条件，即存在常数M，使得对于任意s,t∈ ［a,b］,s＜t，有则式（8）和式（12）成立.