智能扫地机器人的全覆盖路径规划

黄月琴，罗兵，邓辅秦,，李伟科，杨勇

（1.五邑大学 智能制造学部，广东 江门 529020；2.深圳市杉川机器人有限公司，广东 深圳 518000）

扫地机器人是目前应用较广泛的机器人产品，对全部清扫区域的全覆盖路径规划，是扫地机智能化研究的内容之一.该优化问题在遥感拍摄、大面积对象自动检测、自动喷涂等自动控制技术应用中是共性问题，统称为全覆盖路径规划（Complete Coverage Path Planning，CCPP）[1-2].对CCPP问题的解决方案主要分为3类：栅格地图法、单元分解法和两者相结合的方法[3-6].由于栅格地图法还有待解决移动死区问题，单元分解方法是目前解决CCPP问题效果最好的方法[7-9].

单元分解方法先将一个有界单元分解为一组互不重叠且不包含障碍物的单元，再进行单元内路径优化，最后进行单元间转移路径优化.其中单元分解有梯形分解法、布氏单元分解法（Boustrophedon Cellular Decomposition，BCD）和莫尔斯分解方法等，BCD能有效减少分解后的单元数目[10-13].文献[7]使用 BCD在矿区检测应用中分解矿区地图后再利用神经网络进行路径规划，得到优化的CCPP路径.

在单元内的路径规划中，往复式路径（Back and Forth Path，BFP）能适应任意凸多边形且计算简单而被广泛应用.为了寻找单元内最优BFP路径，Huang[3]提出了最小倾向和方法（Minimal Sum of Attitudes，MSA），通过寻找平行于某一条边界的扫描线，使得 BFP路径转弯次数更少.最近，Vasquez-Gomez等人[5]提出了旋转卡壳路径规划方法（Rotating Calipers Path Planner，RCPP），可以快速找到凸多边形的最佳BFP，比其他方法更为高效.RCPP方法算法复杂度低，适合在嵌入式设备中使用.

在单元间的转移路径规划方面，文献[14]基于蚁群算法和遗传算法的优化方法被采用，设计了玻璃幕墙清洁机器人的CCPP.但现有的单元间转移路径优化方法没有考虑单元内路径优化，而且单元内BFP路径有多个较优解时未考虑不同单元起始点，这些缺点降低了全局优化效果.

基于单元分解的 CCPP在单元内、单元间路径规划时已取得了较好的效果.但对于复杂形状的凹区域划分过于琐碎，未考虑相邻区域的总体规划[13].另一方面，在扫地机器人的实际应用中，机器人的转弯和调头都会影响其移动速度，需要额外能耗和时间[15].为此，本文将在3个方面进行改进：首先在路径规划代价函数中加入转弯和调头的代价；其次在单元分解时，对于可以和相邻区域统一规划的凹区域不再分解；单元内路径规划兼顾单元间的转移路径规划，全局优化结合全搜索和蚁群算法.

1 路径代价函数和地图单元分解的改进

本文以深圳市杉川扫地机器人为研究对象，实验场地为室内封闭环境.机器人直径34.5 cm，形状为圆形.在此应用条件下设计了符合扫地机场景的实际代价函数，评估覆盖路径开销.另外，在仿真地图环境中，单元分解数目过多时采用合并相邻且尺寸小的单元.

1.1 路径代价函数改进

传统路径优化目标只考虑路径长度最短，规划时代价函数是起点和终点之间欧氏距离[5-6].但在扫地机实际应用中，相同距离的直线移动和带转弯的移动所花时间和功耗均不相同，转弯前须减速，转弯后重新加速，转弯会带来更多的能耗和时间开销[15].Theresa[4]提出综合转弯次数、机器人半径、路径偏移量和区域边界线角度的距离代价函数.这一方法更符合实际情况，准确评估路径的总代价.不同于无人机转弯时可以超越环境边界，扫地机工作空间是封闭环境，转弯时被限制在距离边界机器人半径的距离内.因此，本文基于文献[4]的代价函数设计新的代价函数.

通过实验测试发现，保持均速移动时，扫地机每次转弯的时间开销是大致相当的.杉川扫地机移动速度为0.8 m/s，同时移动两个扫地机器人，其中一个有一次直角转弯累计移动距离10 m，另一个无转弯直线移动同样时间内移动了10.45 m.类似的大量实验表明：对于0.8 m/s移动速度的扫地机器人，每次转弯的开销可以折合为0.45 m.类似条件下的测试也显示，调头的开销大约是0.49 m.本文将一次转弯、调头的开销，线性折合为路径长度，折合系数分别是ct=0.45 m/次、cr=0.49 m/次.系数值可根据不同扫地机器人进行调整.

通过将转弯次数、调头次数折合为移动距离的方法，将多目标优化方法转化为单目标优化方法.代价函数如下：

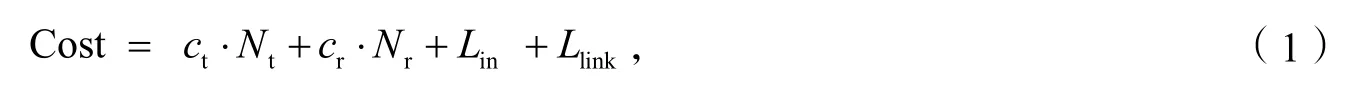
其中ct为转弯代价系数，Nt表示转弯次数，cr为调头代价系数，Nr表示调头次数，Lin是分解的n个单元内的路径长度之和.

每个单元的路径长度Lin(i)按欧氏距离计算：

Llink表示n个单元之间的转移路径长度：

通过代价函数的改进，在路径优化中，不仅追求路径长度最短，还会寻找转弯、调头次数更少的路径.

1.2 地图单元分解的改进

传统单元分解原则是将凹多边形分解为多个凸多边形，然后在凸多边形内分别进行路径规划，最后在单元间规划转移连接路径[3,5].这样虽然可以实现路径长度优化，但会导致分解过于细碎、路径转弯多、调头多，难以达到总体最优，如图1-a.实际上，很多凹多边形仍然是可以进行路径规划寻优的.为此，我们改进为：对于存在一组平行线路径可以全覆盖的凹多边形，不再分解，这样将减少分解单元数量，原多个相邻单元总体进行路径规划将减少路径转弯、调头次数，连接路径也缩短，如图1-b.

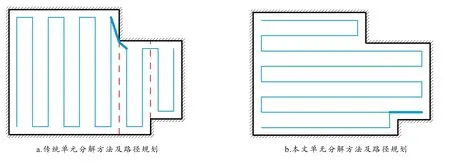
图1 不同单元分解方法对比及路径规划效果

图1中的虚线是单元分解线，传统方法将图1的凹多边形分解为3个矩形，各单元采用式（1）代价函数进行路径规划，如图1-a，路径多了一段两个单元间的连接线，转弯次数为21次.本文方案不再分解该凹多边形，路径如图1-b所示，有一段重复路径，转弯次数为14，调头1次.两种方案的代价计算结果见表1.可见，避免过于细碎的单元分解可以减少转弯、调头次数，路径规划效果更优.

表1 不同单元分解方案的路径规划结果对比

2 路径优化

2.1 凸多边形区域的路径规划

对于凸区域路径规划，文献[5]中的RCPP方法可以快速求得无人机场景中的最佳BFP，但是不适用于扫地机场景，而且寻优时路径代价未计算转弯次数.故本文采用 RCPP时，将路径点限制在边界内，并使用公式（1）作为代价函数选择最优路径.

被分解后的区域中包含凹、凸单元，记多边形Q=｛V,E｝，V=｛ 1,2,…,n｝是顺时针的凸多边形顶点集合，E=｛(1,2),(2,3),…,(n-1,n),(n,1)｝是由V中元素组成的边.多边形的区域为A(Q)，设扫地机的一条路径s的覆盖区域为C(s).对于 2D凸多边形的一条覆盖路径ρ需满足C(ρ)⊆A(Q).具体算法步骤如下：

1）计算凸区域的顶点集合Q=｛V｝的对踵点集合A=｛(i1,j1),…,(in,jn)｝；2）对于步骤1）中A中的每对对踵点，使用顺时针卡壳和逆时针卡壳分别计算出两条 BFP，返回总长度最短的路径；3）针对A中对踵点下的路径，根据式（1）选择长度最短的路径作为凸区域的BFP；4）获得全覆盖凸区域的路径ρ.

步骤 1）中的对踵点对是凸多边形上的一对顶点，过这对点的一组平行线可以将凸多边形夹在这两条平行线中间，或落在平行线上.图2展示了该凸多边形的6对对踵点和对应BFP.图中的虚线表示穿过对踵点的平行线，图2-a中路径起始于标号（0,4）的边，向垂直于（0,4）边往2顶点的方向移动.

步骤2）计算每对对踵点(in,jn)的BFP长度，分别使用顺时针RCPP和逆时针RCPP方法，即过该对踵点的平行线对寻找首次与多边形接触的边，这条边称为基线.顺逆旋转得到的基线分别记为(b1,b1+1)和(b2,b2+1)，而路径远端的顶点为相应的对踵点a1和a2.因此一对对踵点有两种 BFP.尽管是同一个凸区域，不同方向的RCPP方法得到的规划路径长度会有不同，在保证覆盖率的情况下，路径长度短的更适用于能量有限的扫地机.因此，保证每一个分解后的单元内路径最优，比较d1和d2的大小.两者距离点到直线公式和最短路径决策如式（4）和（5）.计算图2的每对对踵点的路径总代价分别为948.48 m、985.09 m、1072.18 m、1072.67 m、995.82 m、949.39 m，选择代价最小的路径作为该凸边形的覆盖路径.

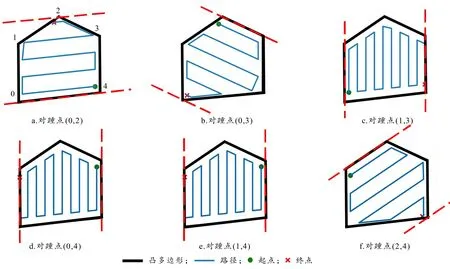
图2 凸多边形对踵点下的各种路径情况

2.2 凹多边形区域的全覆盖路径规划

凹多边形区域的覆盖路径规划采用直接法（Direct Method，DM），算法描述如下：

1）初始化凹多边形的上下边界点集C={(x1,y1),(x2,y2),…,(xn,yn)}、F={(x1,f1),(x2,f2),…,(xn,fn)}、运动方向向下和扫地机半径r；

2）单元的最左端线段L向右偏移r，L的横坐标为xcurrent=xleft+r.运动方向向下，此时路径ρ中加入路径点(xcurrent,ycurrent-r),(xcurrent,fcurrent+r)，更改运动方向向上.若方向向上路径ρ中加入路径点(xcurrent,fcurrent+r),(xcurrent,ycurrent-r)，更改运动方向向下；

3）位于xcurrent的扫描线继续向右平移d=2r.若向下运动，路径ρ加入路径点集合{(xcurrent,fcurrent+r),(xcurrent+1,fcurrent+1+r),…,(xcurrent+d,fcurrent+d+r)}，更改运动方向向上.若向上，路径ρ加入 {(xcurrent,ycurrent-r),(xcurrent+1,ycurrent+1-r),…,(xcurrent+d,ycurrent+d-r)}，更改运动方向向下.更新xcurrent；

4）重复步骤2）直至L到达单元的最右端xright；5）若为向右运动，路径为ρ.若向左，逆序排列路径点；6）获得覆盖凹区域路径ρ.

2.3 单元间的统一优化及转移路径优化

通过以上两节可以获得单元内的优化路径，但各单元内路径优化没有考虑单元间的转移连接路径.特别是当单元数目较多时单元间的转移路径长度对全覆盖的路径总长度影响更大.图3展示了不同的路径组合产生不同的路径代价，图3-d的路径代价最小，与代价最大的图3-a相差141.99 m，超过路径总长度的 10%.当单元间的转移路径选择最短的路径组合时，必然会缩短整体区域的覆盖路径长度.

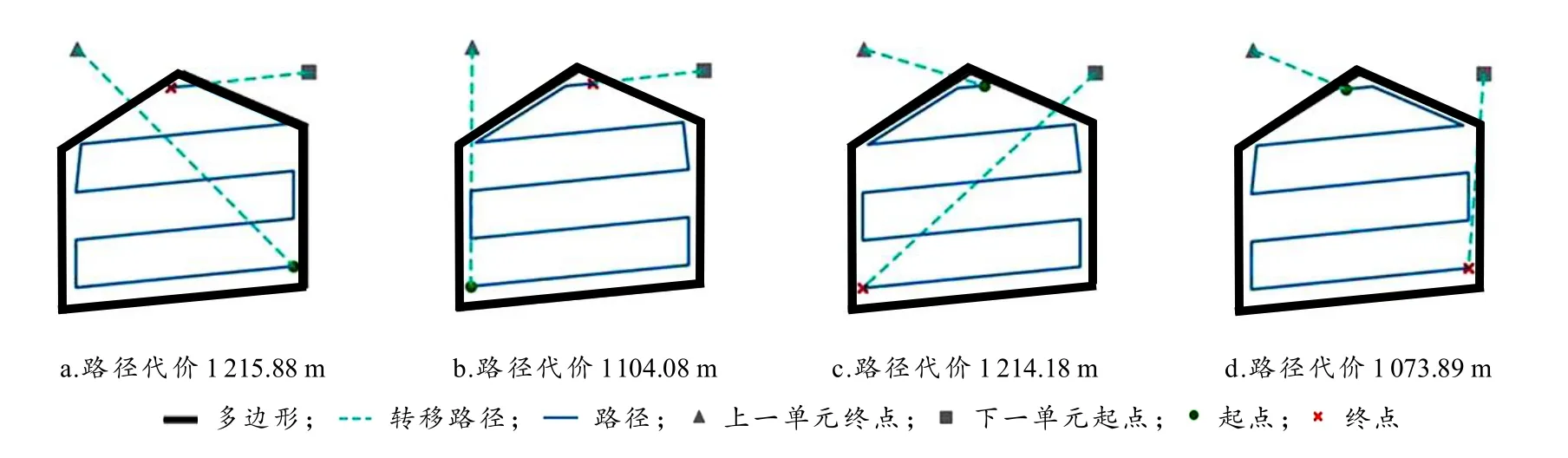
图3 一个单元的4种起始点组合

文献[1]运用蚁群算法较好地解决了水下机器人的CCPP问题中的单元间的连接优化，但对于单元内的多种优化路径对单元间的影响没有考虑.为此，本文采取全搜索结合蚁群算法来进行优化，具体方法是：

1）保留每个单元内不同起止点的多个较优解，与相邻单元统一进行组合优化；

2）确定每个单元的起点、终点、优化路径；

3）当单元数较少，或比较选择的组合数量较少时，采用全搜索选择最优解，当单元数量较多或组合选择多难以全搜索时，采用蚁群算法进行寻优.

3 仿真实验及结果分析

由于扫地机器人主要是针对家庭使用，本实验选取了8种具代表性的家居布局以及2种特殊设计的布局。来进行CCPP仿真实验，仿真实验运行于Python环境，扫地机直径设置为34.5 cm.分别使用平行于垂直方向扫描方向DM方法+遗传算法[6]、RCPP方法+蚁群算法[5,16]和本文方案对已知地图进行CCPP对比实验.

本文方案首先使用改进 BCD方法对二维平面地图单元分解，其中一种特殊设计的布局地图获得的单元分解结果如图4-a所示，黑色表示不可达障碍区域，虚线代表单元边界.然后使用式（1）和相邻单元间统一优化等改进方案进行路径优化，最后得到的优化路径结果如图4-b所示，图中圆点和交叉分别代表单元内路径起点和止点，虚线表示单元间转移路径，实线代表扫地机路径.

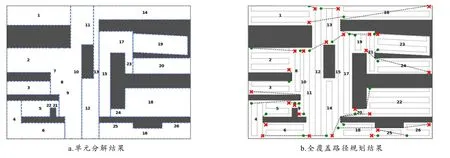
图4 本文方案的单元分解和全覆盖路径规划

本文改进的单元分解法分解为12个单元，传统方法分解为26个单元.对该布局的 DM方法+遗传算法、旋转卡壳RCPP方法+蚁群算法进行的对比实验结果如图5所示.

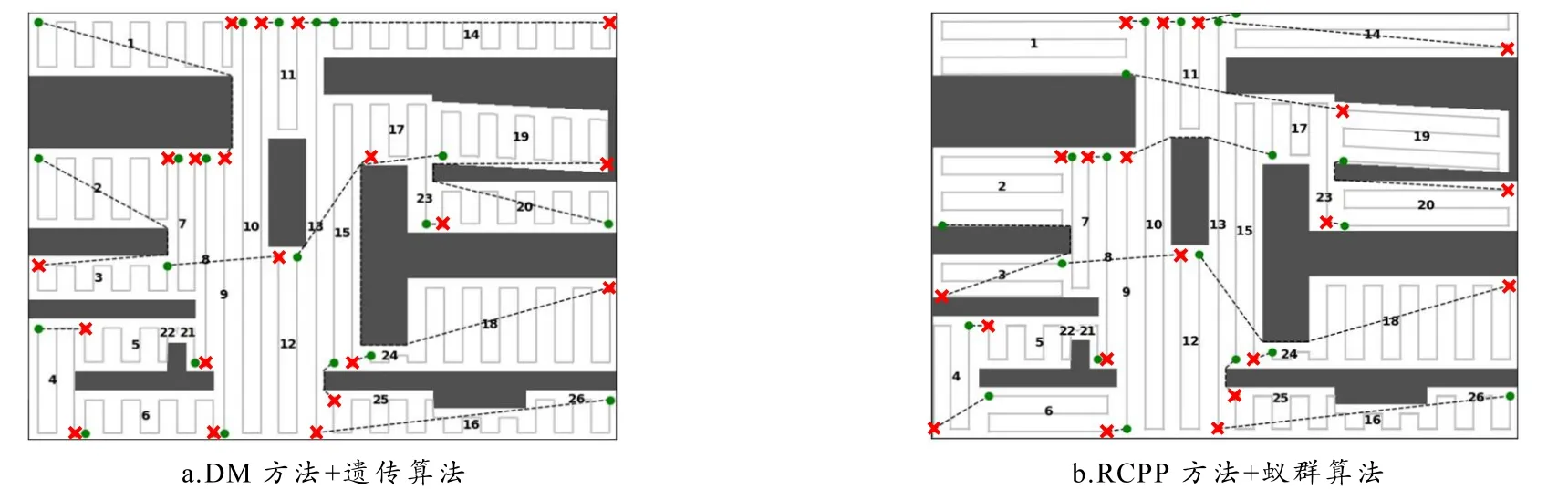
图5 对比的全覆盖路径规划结果

3种方案的总覆盖平均路径总代价、平均转弯数目、平均Lin和平均Llink的统计结果如表2所示.结果表明DM方法的路径代价最大，使用本文方案转弯数最少、路径总代价最小.

表2 3种方法的全覆盖路径规划结果

由于DM方法仅使用垂直扫描方向，故当单元的水平跨度大于垂直跨度时，其路径不是最优的，导致单元内转弯次数增大.RCPP方法在凸区域内可以得到最佳BFP，但拆分所有非凸区域为凸区域增加了单元间的转移路径和转弯次数.实验结果表明，本文方案更适合复杂环境的CCPP.

4 结论

本文设计了考虑转弯、调头开销的CCPP代价函数，并以简单线性系数将其转化为路径长度，有利于优化比较.在单元分解时采用了可规划凹区域不再分解方法避免过于细碎的分解，减少转弯次数和单元间连接路径长度.单元内优化考虑了相邻单元间的统一优化和连接，并采用全搜索和蚁群算法进行优化.仿真实验表明，本方案比传统方案减少了转弯次数，总体优化效果更好.但是由于使用实验的扫地机器人型号有限，转弯、调头代价的实验规模均不够，后期通过更多的实验，有望建立更合理的转弯、调头代价函数.另外，单元间的统一优化、转移路径优化算法对于存在多单元时仍有待改进.