静载试验方法在水闸地基土体抗拔变形量计算中的应用

2021-07-09王丹丹

水科学与工程技术 2021年3期

王丹丹

（辽宁省盘锦水文局，辽宁盘锦 124010）

水闸地基受土体抗拔变形影响较为明显，因此在进行水闸地基稳定性设计时需对其土体的抗拔应力进行分析，从而分析其抗拔受力变形程度［1］。近些年来，虽然对于水闸地基稳定性研究在逐步深入［2-8］，但这些成果大都未能对其土体的抗拔应力进行分析。在其他工程领域，其地基土体的抗拔应力已逐步开始研究［9-15］，这其中静载试验方法应用较为成熟，但在水利工程方面还未得到相关应用，为此本文结合辽宁地区某水闸工程实例，对其土体抗拔应力进行分析，从而分析该方法对水闸地基土体抗拔受力变形的影响程度。研究成果对于水闸地基土体稳定性设计具有重要参考意义。

1 研究方法

静载试验方法对水闸地基的土体进行极限抗拔变形的计算分析，分析方程为：

式中 ΔT为切向应力（kPa）；ϕ为内摩擦角（°）；c为黏聚阻力（kPa）；ΔL为土体滑面宽度（mm）；ΔR为法向应力（kPa）。法向应力计算方程为：

式中 Kp为侧向应力系数；θ为水平矢量夹角（°）；ΔQ为法向应力（kPa），其计算方程为：

式中 γ为土体总量（kg）；Z为纵向深度（mm）；H为横向位移（mm）。对水闸土体静力荷载进行计算：

式中 x为中心点距（mm）；Δx为变化距离（mm）；μ为圆周破坏比；Pv为静力荷载（kPa）；q为受力单元的计算荷载（kPa）。

对土体的静力荷载进行极限求解计算：

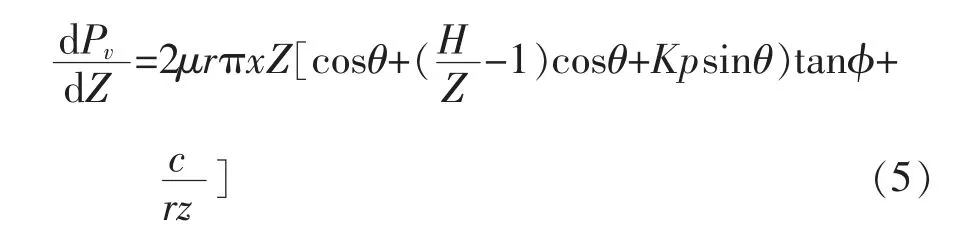
对水闸地基土体承载应力计算的方程：

式中 WP为地桩质量（kg）；L为地桩长度总值（m）；τmax为剪切应力最大值，其计算方程为：

式中 ϕ′为倾斜转角（°）；K为垂向应力参数。

2 工程实例分析

2.1 土体结构参数

以辽宁某水闸建设为实例，对其水闸地基土体的抗拔应力进行探讨，该水闸采用4根桩体进行加固，各桩体地基土层的主要参数如表1。

表1 水闸地基土体参数情况

2.2 水闸地基土层位移分析

分别采用传统原位观测和静载试验方法对不同地基开挖深度下的土层位移进行对比计算，结果如表2。

表2 不同开挖深度下的水闸地基土层位移对比计算结果

从不同开挖深度下的水闸地基土层位移对比计算结果可看出，传统采用原位测定方式的不同开挖深度的土体和桩体变形位移量都要高于静载试验方法计算的位移量，这主要因为静载土体自重影响所致，使得水闸地基土体和桩体位移较传统原位观测方法有所减小。土体抗拔应力随开挖深度递增而有所减小，土层弹性模量受桩体位移影响较为明显，水闸地基土体外扩形变主要出现在开挖深度低于4.5m以后。

2.3 水闸地基土体抗拔变形量分析结果

分别采用传统原位观测方法和静载试验方法对水闸地基不同变形量下的抗拔变形量进行对比分析，计算结果如表3。

表3 不同方法变形量计算对比结果

从不同方法变形量计算结果对比结果可看出，基于静载试验方法下水闸地基土体不同观测变形量下的计算误差均低于25%，而传统原位观测方法下其误差均要高于静载试验方法，静载试验方法的变形量计算误差平均降低8.6%，这主要是因为静载试验方法可考虑水闸土体地基自身重力的影响，使其不同抗拔变形条件下的土体变形计算精度更高。