定向分布纤维增强混凝土的制备和力学性能分析

刘志勇，谢 娟

（1.石家庄理工职业学院，河北 石家庄 050228；2.河北科技大学化学与制药工程学院，河北 石家庄 050018）

1 引言

超高性能纤维增强混凝土（UHPFRC）[1-5]是新型水泥基复合材料，钢纤维有效改善了混凝土的脆性，增强了混凝土的机械强度。在UHPFRC 中，钢纤维通过吸收裂纹扩展能和桥接作用，有效阻碍了混凝土内部微裂纹的伸展，从而提高混凝土的抗压、抗弯和抗扭等机械性能[3-5]。然而，常规制备方法中，由于浇筑时混凝土中钢纤维杂乱无章，仅有部分钢纤维起到了增强作用[6，7]。

在前人的报道中，混凝土中纤维的分布与取向对混凝土的性能有着重要影响，使得纤维增强混凝土的机械性能出现各向异性，沿钢纤维方向的抗压强度远远大于沿纤维垂直方向，这有利于充分利用钢纤维[8-10]。Lee[11-13]等人通过恒定磁场控制混凝土拌合物中的钢纤维方向，制备出单向分布钢纤维混凝土，并初步提出纤维取向统一系数和纤维方向效应系数。国内慕儒团队[14-18]对此开展了大量研究，对单向钢纤维混凝土的制备和性能做了大量研究。然而，他们都是利用恒定磁场磁化方法，耗时长，单次成品量低，远远达不到工业生产的要求。

本研究中提出了新的制备方法。首先通过添加超塑剂，制备了超高流动性混凝土。在此基础上通过浆体流动时的内摩擦力，使钢纤维方向趋于一致，制备定向分布混凝土。通过制备钢纤维不同掺量的普通和定向分布混凝土，比较其纤维取向系数和力学性能，研究定向分布钢纤维的性能。为此，本文设计了不同钢纤维掺量（0、0.3、0.6、0.9、1.2、1.5、1.8Vol.%）不同钢纤维分布和取向（0°、15°、30°、45°、60°、75°、90°）的混凝土，分析了UHPFRC 中抗压强度、抗折强度与钢纤维掺量、分布和取向的相关性。

2 试验

2.1 原材料和配合比

本试验所采用的原料和外加剂符合国家标准《硅酸盐水泥、普通硅酸盐水泥》（GB/T 175-2007）的规定。水泥为堡垒牌P.O52.5 硅酸盐水泥，粉煤灰为Ⅱ级粉煤灰，硅灰为H 系硅灰，骨料采用细度模数为0.92 和1.78的两种石英砂，各种原材料成分及粒径大小分布见表1、图2。钢纤维的长径比为65，直径为0.2mm，其物理性能如表2和图1所示。此外所用固体聚羧酸高性能减水剂，实测减水效率为24%。

表1 原料主要成分及粒径

表2 钢纤维的主要性能

图1 钢纤维形貌

2.2 试验方法

2.2.1 混凝土设计

UHPFRC 的设计理论是最大堆积密度理论（densified particle packing），依据改进的Andreasen 和Andersen（A＆A）[19-21]模型来计算每种原料的使用量，如式（1）所示。当分布系数q＜0.25 时，用于细骨料混凝土，考虑到

纤维增强混凝土中大量使用细骨料因此将分布系数q定为0.23。

其中：P（D）—筛下物料的累加所占总物料的百分百；

D—物料的粒径，μm；

Dmax——物料中的最大颗粒直径，μm；

Dmin—物料的最小粒径，μm；

q—体系中物料的分布系数。

在本次研究中所使用的配比见表3；角度设计见表4；UHPFRC 的目标和优化分级曲线之间的推导如图2所示；同时为了表征钢纤维在混凝土中的分布状态和测试时的分布状态，建立三维模型，如图3所示。

图2 最紧密堆积模拟曲线

图3 试块三维坐标

表3 基准组配合比设计 kg/m3

表4 定向分布角度设计（°）

2.2.2 材料制备

UHPFRC 中纤维分布主要受铸造工艺和周边环境影响。因此为了更好的优化混凝土中钢纤维取向和分布的影响，本试验采用新的外加磁场铸造工艺[16-17]。为使钢纤维在磁场中受到更大的磁力作用，以及更好地分散效应，钢纤维需在强磁场磁化。为减少浇注环境对钢纤维的影响，本试验采用有机模具，并在木质振动台浇注。本研究的制备原理如图4所示。为探究钢纤维在磁场中的动态移动过程，通过改变新拌混凝土的有效震动时间，观测在某一时间点钢纤维的取向和分布。

图4 制备原理图

2.2.3 养护条件

本试验试块和养护条件按照国家标准《水泥胶砂强度检验方法》（GB/T 17671-2016）的相关规定，尺寸为40mm×40mm×160mm，浇铸后24h 拆模，养护条件为室温（20±2）℃，湿度（50±5）%，养护时间为28d。

2.3 测试方法

2.3.1 力学性能测试

依据《水泥胶砂强度检验方法》（GB/T17671-2016），测试仪器为NYL-300 型压力试验机，测试抗压强度时压力试验机的加载速率为2.4kN/s。抗折时加载速率为2.0kN/s。

2.3.2 纤维取向测试

为了评估UHPFRC 中纤维分布和取向，将破碎后的混凝土试块切片，使用数显倾斜度测量仪对界面中钢纤维进行角度测量，以每5°为一个区间进行统计。

3 结果和讨论

为了分析钢纤维在UHPFRC 中的取向与分布，已经对试块建立了三维坐标体系，如上文所述，为了对纤维取向和受力分布影响之间建立更加清晰的对应关系，本文采用数学归纳的方法进行分析。

3.1 纤维分布状态影响评估与分析

探究在UHPFRC 中钢纤维在不同掺量下，外加磁场诱导时间的不同，评估钢纤维在磁场中的运动状态和分布状态。根据纤维运动理论[9-10]，在新鲜混凝土浆体中，纤维的运动受到重力、浮力、扰流阻力和磁场力的共同作用，运动状态如图5所示。为了表征纤维的分布状态，引入钢纤维混凝土的纤维方向统一系数因子公式[1]，如式（2）所示，测试结果如图6、图7和图8所示。

图5 钢纤维受力分析

图6 不同钢纤维掺量下抗压强度发展

图7 不同钢纤维掺量下抗折强度的发展

图8 不同钢纤维掺量下强度增长率

式中：为直钢纤维的长度，mm；

为直钢纤维与试件设计方向的夹角，°；

UHPFRC 试块抗压/抗折强度强度如图6、图7 所示，试验结果证明，纤维增强混凝土的破坏强度与纤维的掺量呈正相关。如图8 所示，纤维掺量在0.3～1.2vol.%范围内，增长率较快，在0.9 vol.%时，达到最大强度增长率；当纤维掺量大于1.2 vol.%时，强度增长率随纤维掺量的增加而逐渐减少。结果与Lee 和慕儒团队[11，16]等的研究报告基本一致；其研究报告中提出纤维增强混凝土中钢纤维最优掺量在1.0 vol.%左右。根据英国20 世纪90 年代提出的“混凝土复合材料机理”，钢纤维在低掺量时的主要作用是阻碍混凝土内部的微裂纹扩展和阻止宏观裂纹的发生和发展；当钢纤维掺量大于最优掺量，钢纤维反而会改变混凝土骨架结构，不利于强度的增长。

混凝土中纤维取向统一系数与磁场引导时间如图9 所示。试验结果表明，纤维取向统一系数与引导时间基本成正相关关系。2～7 组试验达到最大取向系数的时间依次为10min，15mim，15min，20min。这一结果与Lee 等人[11]的研究报告基本一致；慕儒[16]研究报告中变化曲线基本相同，引导时间不同，这可能与制备时的磁场力强度、阻滞力有关。根据纤维受力分析，如图9 所示，随磁场角度变化，磁场磁矩逐渐变小；随运动状态改变，扰流阻力先减小后增大，综合受力分析结果，前期动力大于阻力，必然会有加速阶段，后期阻力大于动力，必然会有减速到0阶段。

图9 纤维取向统一系数与磁场引导时间

3.2 纤维取向效应因子

3.2.1 方向效应因子

如前文所述，UHPFRC 中钢纤维方向定向分布时，机械强度也会发生变化，并呈现出规律的各项异性。为了更好地表征纤维取向与机械强度之间的关系，本文引入纤维取向效应因子，表征机械受力破坏过程中，纤维取向对受力过程的自身贡献系数。Lee[8]等人提出了方向效应因子概念，并提出钢纤维在混凝土中三维随机乱向分布时的方向效应因子公式αs，如式3所示：

其中：为直纤维的长度，mm

为XY二维平面中直钢纤维与Y轴的夹角，°；

φ为YZ二维平面中直钢纤维与Y轴的夹角，°。

因此，纤维取向抗折效应因子αs的有效取值区间为0～1，且可以推导出当纤维在混凝土中完全自由随机分布时，取向因子αso（完全随机分布状态的理论基准值）应该为0.405。

本次试验实际计算时发现，纤维取向因子αso实的值为0.509，与αso存在差异，具体原因分析如下：

①重力效应。

在实际搅拌浇注过程中，因为纤维的长径比非常大，在重力和震动的作用下，钢纤维在浆体中会发生转动，趋向重力垂直的平面转动的趋势，在本文坐标系中体现为向XY 平面转动，因此，钢纤维在不同平面与Y轴的实际夹角不同程度的小于理论夹角，使αso实大于αso。

②边界和内部骨料碰撞效应。

钢纤维本身的抗折强度不高且长径比过大，当搅拌、浇注时，如果存在钢纤维与模具的边界碰撞或者不同骨料之间形成简支梁效应时，钢纤维会发生弯曲变形，因此会对取向系数造成不利影响，影响较大，不可忽略。

3.2.2 纤维取向效应因子与强度的关系

为了更好的表征UHPFRC 中纤维定向分布时，纤维分布方向与机械强度之间的关系，本文在此理论基础上，结合三维模型的受力分布状态，对公式进行了修正，提出了三维定向纤维方向效应因子系数公式，抗折强度效应因子系数α，如式（4）、式（5）所示：

其中：l为直钢纤维长度，mm；

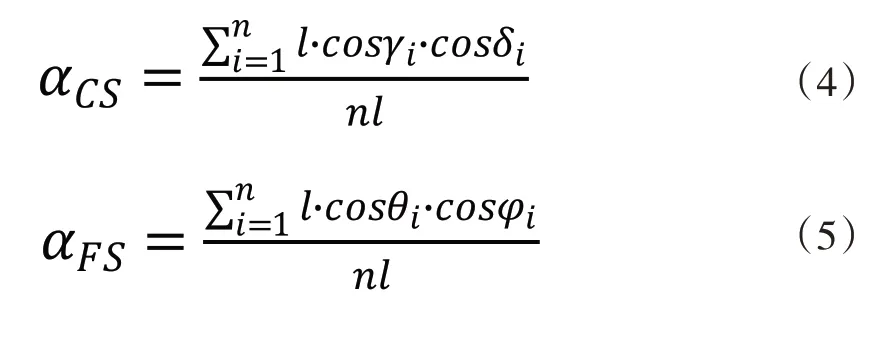
γi为在XZ二维平面中直钢纤维与Z轴的夹角，°；

δi为在YZ二维平面中直钢纤维与Z轴的夹角，°；

θi为在XY二维平面中直钢纤维与Y轴的夹角，°；

φi为在YZ二维平面中直钢纤维与Y轴的夹角，°；

n为横截面纤维的总数目。

由图10 可知，当钢纤维掺量为0.9Vol%时，随效应因子系数的增大，混凝土抗压强度逐渐增大，达到最大强度后抗压强度迅速下降。在UHPFRC 中，钢纤维主要作用是阻碍混凝土内部的微裂纹扩展和阻止宏观裂纹的发生和发展；同时根据混凝土复合材料理论[8-10]，钢纤维的拉伸强度为2000MPa，远大于混凝土基体拉伸强度，复合后的强度会远大于混凝土基体。本文主要运用这两种理论分析。在αFS在0～0.50 区间时，抗压强度基本没有变化，其主要原因是，在此区间内，钢纤维与XZ 平面夹角基本上α≥60°，裂纹扩展方向基本沿XZ平面延伸，钢纤维与裂纹之间呈大夹角，阻裂能力基本无变化；同时，当受力破坏时，纤维与受力方向呈大夹角，基本没有发生拉伸作用。当αFS在0.50～0.90 区间时，抗压强度迅速增大，其主要原因是：在此区间时，钢纤维与XZ 平面的夹角25°≤α≤60°，裂纹扩展方向基本沿XZ 平面延伸，钢纤维与裂纹之间夹角逐渐减小，阻裂能力降低，对混凝土机械强度的促进作用缓慢减弱；同时，当受力破坏时，纤维与受力方向夹角逐渐下，拉伸作用迅速提高，对钢纤维机械强度的促进作用快速增强；两种作用中，拉伸作用的促进效率远远大于前者的减弱效率。αFS在0.50～0.90 区间时，抗压强度迅速降低，其主要原因是：在此区间时，钢纤维与XZ 平面的夹角0°≤α≤25°，裂纹扩展方向基本沿XZ 平面延伸，钢纤维与裂纹之间夹角继续减小，阻裂能力降低，对混凝土机械强度的促进作用快速减弱；同时，当受力破坏时，纤维与受力方向夹角逐渐下，拉伸作用迅速提高，对钢纤维机械强度的促进作用继续增强；两种作用中，阻裂作用的减弱效率远远大于后者的促进效率；同时钢纤维取向与裂纹扩展方向基本一致，改变了混凝土的骨架结构，加快了裂隙的扩展。

图10 抗压强度与取向系数

由图11 可知，当钢纤维掺量为0.9Vol%时，随着效应因子的增大，抗折强度逐渐增大，但是变化率不同。在αcs在0～0.70区间时，抗折强度增长缓慢，其主要原因是：在此区间内，钢纤维与XY 平面夹角基本上α≥45°，裂纹扩展方向基本沿XZ 平面延伸，钢纤维与裂纹之间呈小夹角，阻裂能力缓慢增长；同时，当受力破坏时，纤维与受力方向呈小夹角，拉伸作用增长缓慢。在αCS在0.70～1.0 区间时，抗折强度增长迅速，其主要原因是：在此区间内，钢纤维与XY 平面夹角基本上0°≤α≤45°，裂纹扩展方向基本沿XZ 平面延伸，钢纤维与裂纹之间呈大夹角，阻裂能力快速增大；同时，当受力破坏时，纤维与受力方向呈大夹角，拉伸作用快速增长。

图11 抗折强度与取向系数

由图9、图10可知，在钢纤维最优掺量时，钢纤维定向分布UHPFRC 的最大抗压强度/抗折强度均远大于钢纤维随机分布UHPFRC，抗压强度提升14.10%，抗折强度提升48.02%。其主要原因是：在两种机械破坏测试时，钢纤维都起到了良好的拉伸作用，提高复合强度；但是抗折破坏时，钢纤维起到良好的阻裂效果；抗压破坏时，钢纤维没有起到良好的阻裂效果，甚至加快了裂隙的发展。这与Lee[11，16]等人的报道基本相同。

当αs=0.509 时，在不同钢纤维掺量下，钢纤维随机分布混凝土和钢纤维定向分布混凝土强度对比如如图12、图13 所示。结果表明，当αs系数相同时，钢纤维定向分布混凝土强度都小于钢纤维随机分布混凝土。其主要原因是：钢纤维之间的相互堆叠，增强了钢纤维对混凝土基体的阻裂作用。同时发现，在钢纤维最优掺量附近时，二者强度差最大。其主要原因可能是：在钢纤维最优掺量时，阻裂作用下降幅度大。

图12 钢纤维不同分布状态下抗压强度对比

图13 钢纤维不同分布状态下抗压强度对比

4 结语

本文利用磁场引导钢纤维在混凝土中的取向与分布，探究UHPFRC 中钢纤维取向与分布对机械强度的影响。研究发现，UHPFRC 中钢纤维最优掺量为0.9 Vol%，可能会改变混凝土骨架结构，不利于强度的发展。当钢纤维在最优掺量时，随着钢纤维取向系数的增大，UHPFRC抗压强度先增大后减小；其主要原因是：钢纤维拉伸作用的增强和阻裂作用的减弱，甚至加速裂纹的发展。当钢纤维在最优掺量时，随着钢纤维取向系数的增大，UHPFRC 抗折强度持续增大；其主要原因是：是钢纤维拉伸作用的增强和阻裂作用都在增强。当取向系数αs=0.509 时，不同钢纤维掺量下，钢纤维定向分布UHPFRC 的抗压强度/抗折强度均小于钢纤维随机分布UHPFRC；其主要原因是：钢纤维乱向分布时，相互之间的堆叠强化了阻裂作用。不同钢纤维掺量下，钢纤维定向分布UHPFRC 的最大抗压强度/抗折强度均远大于钢纤维随机分布UHPFRC，抗压强度提升14.10%，抗折强度提升48.02%；其主要原因是：在两者机械破坏测试中，钢纤维的阻裂作用明显存在差异。