基于社会关系的群智感知任务分发机制

张文东 石刚 田生伟 钱育蓉

(1．新疆大学 软件学院，新疆 乌鲁木齐 830091；2.新疆大学 信息科学与工程学院，新疆 乌鲁木齐 830046)

近年来，随着无线通信技术和传感器技术的不断发展，搭载各类传感器的移动智能终端设备得到了迅速的普及，群智感知也逐渐成了复杂环境下数据统计分析与增强理解的一种有力的新途径[1]。群智感知是以人为中心的城市感知系统[2- 3]，作为感知节点的移动用户是完成参与式感知任务的关键，他们通过携带的移动设备为数据需求方提供了所需要的感知数据，同时移动用户的移动特性使移动用户可以不受时间与地点的约束来完成感知数据的采集工作，这实现了对现实物理世界的全面覆盖和感知，因此如何将感知任务分发给移动用户是参与式感知过程中非常重要的过程。

群智感知任务分发作为群智感知中一个重要的研究方向目前已被广泛地研究[4- 7]，Pournajaf等[8]基于公开的轨迹历史建立移动性模型，提出了一种用于移动群智感知中的空间任务分配的新颖模型，该模型使用动态和自适应的数据驱动方案以接近最优的方式将感知任务分配给具有不确定轨迹的移动参与者；Zhou等[9]针对路线规划和任务分配问题，将制定的优化问题转换为两阶段匹配问题，其中第一阶段基于动态规划(DP)或遗传算法(GA)解决路线规划问题，第二阶段，通过探索Gale-Shapley(GS)算法解决分配任务的问题。

尽管现有研究能够很好地进行感知任务分发，但仍存在着不容忽视的问题：一是可能会出现招募到的感知任务参与者不足的情况，严重影响任务的完成；二是不能形成一条持久稳定的任务分发链路，严重影响群智感知系统的性能、效率以及健壮性。鉴于此，本研究基于社会关系理论，借助社区的稳定性和任务分发的可靠性，提出了一个基于社会关系的群智感知任务分发机制。首先提出了基于节点社会属性的相似度量化算法(Intimacy Quantification Method Based on Social Attributes,IQSA)；然后结合信息熵理论与社会关系提出了一种基于信息熵相似度的社区检测算法(Community Detection Algorithm Based on Information Entropy Similarity，CDIES)；并通过实验对文中提出的算法的性能进行了分析。

1 节点间社会关系的形式化描述

感知节点的位置和移动轨迹是实现任务分发的关键。已有研究表明，节点的移动和节点的社会关系具有很强的相关性。文献[10]通过对节点间社会关系强弱的计算，提出一种基于社会关系的移动用户位置预测算法；文献[11]通过分析移动用户签到位置的语义信息，研究了移动用户间的社会关系。

文中将节点社会属性因子划分为静态和动态两个维度进行分析。通过构造多维语义分级树和空间索引编码，对节点静态属性进行形式化表示，计算节点间的静态相似度；同时，通过分析节点间动态交互因子，结合信息熵理论，计算节点间的动态相似性，最终计算得出节点间的社会关系相似性。

1.1 基于静态特征的静态相似度量化

本研究提出了基于节点社会属性的相似度量化算法(IQSA)，该算法首先对社会关系网络中的节点的静态特征进行分析和量化，并计算节点间的静态相似度；其次根据节点间的动态交互记录计算节点间的动态相似度；最后对静态相似度和动态相似度进行加权计算，得到节点间的相似度以描述节点间的社会关系。

在节点间静态相似度的计算中，首先分析并提取节点的静态特征，例如身份信息、职业信息与位置信息等；然后对节点的静态属性进行组织分层并根据不同的属性构建多类别的多层次语义分析树，对该语义树的每个节点进行二进制编码，静态相似度从每个类别的多层次语义分析树的根节点开始比较，随着语义树深度的加深，节点间的静态相似度也随之增加；最后，在不同类别的语义树中选择相似度最大的值作为节点间的静态相似度。构建好多层次语义分析树之后，根据该语义树得到节点的静态特征码，其形式为GeoHash编码作为高位，低位依次是节点静态特征对应的语义树的第二层、第三层、…，各层之间填充相同的比特位作为间隔。语义树的具体构建和编码方式如图1所示。

图1 新疆大学职业属性语义树

根据静态特征码来量化两者之间的静态相似度，其具体计算如下：

(1)

1.2 基于动态交互的动态相似度量化

定义1 初始动态相似度 设节点p、q之间的交互频率为fp、q，且存在交互频率阈值σ(σ≤fp、q)，则节点p对于节点q的初始动态相似度Sp,q=Ff-/Fσ+，其中Ff-表示与节点p的交互次数介于σ和fp、q之间的节点数，Fσ+表示与节点p的交互次数大于σ的总节点数。

定义2 动态相似度权重指标Wp,q设节点p的总度数为dp，则Wp,q=fp,q/dp。

定义3 动态交互因子 设节点p有k个邻接点并构成邻接点集VN-p=(v1,v2,…,vk)，则p的交互因子可以表示为

(2)

定义4 平均动态交互因子 平均动态交互因子是指在一个社会关系网络中，中介中心度较高的r个节点的动态交互熵的平均值。其中，中介中心度表示该节点处于任意两个节点之间最短路径上的次数与这两个节点之间最短路径总数的比值。为表达方便，记这r个节点构成集合VA=(v1,v2,…,vr)，平均动态交互因子的计算公式如下所示：

(3)

在考虑节点动态相似度的过程中，在节点间交互频率一定时，对于动态交互因子较大的节点，应该赋予较小的权值，对于动态交互因子较小的节点，应该赋予较大的权值。由此文中给定权重的计算公式如下：

(4)

(5)

根据权重和初始动态相似度来计算节点间的动态相似度，计算公式如下：

Dsim_ p,q=Sp,qweight(p,q)+Sq,pweight(q,p)

(6)

其中:Dsim_ p,q表示节点p、q之间的动态相似度;Sp,q表示节点p对节点q的初始动态相似度;Sq,p表示节点q对节点p的初始动态相似度;weight(p,q)表示节点p对节点q的初始动态相似度权重;weight(q,p)表示节点q对节点p的初始动态相似度权重。综上所述，就得到了节点间的动态相似度。

1.3 基于社会关系的相似度计算

计算节点间的相似度需要为两者分配相应的权重并求取加权和，因此计算相似度最后的一个关键步骤就是为静态相似度和动态相似度分配权重。按照层次分析法中1-9标度方法，对Ssim_ p,q和Dsim_ p,q之间的权重关系划分为5个档次，值为1表示Ssim_ p,q和Dsim_ p,q同样重要，值为3表示Ssim_ p,q比Dsim_ p,q稍显重要，以此类推，值为9表示Ssim_ p,q相比于Dsim_ p,q极为重要。根据权重标度表构建权重判别矩阵如下：

(7)

式中：a∈{1,3,5,7,9}，可得到矩阵W的特征向量w=(α,β)T，其中α=1/(1+a)、β=1-1/(1+a)，α、β即为分配给静态相似度和动态相似度的权重。因此，节点p,q之间的相似度为

Simp,q=αSsim_ p,q+βDsim_ p,q

(8)

2 感知任务社区化分发策略

2.1 基于信息熵相似度的社区检测算法

定义5 社区结构community 在参与式感知下的移动节点集组成的社会关系网络拓扑结构中，这些节点通过边连接成对，一些社会关系较为亲密的节点群会相对紧密地连接并聚合成簇或堆，这些簇或堆被称为社区结构。

定义6 节点的度数d节点的度数表示与该节点有相关联系的节点的数量，若两个节点之间的相似度不小于阈值δ，则代表这两个节点之间存在一定的联系，于是用一条边将两个节点连接成为一对，此时这两个节点的度数分别增加1。

定义7 节点加入概率PijPij表示节点j加入到社区i内的概率，具体计算公式如下所示：

(9)

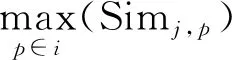
定义8 信息熵相似度ES 信息熵相似度表示社区与社区之间或者社区与节点之间的相似度，根据信息熵理论的定义，ES的值越小，表示社区内节点间的联系越紧密，因此会将信息熵较小的两个社区进行合并。基于信息熵理论，信息熵相似度的具体计算公式如式(10)所示：

(10)

式中的第一部分表示节点j加入到其他社区的信息熵计算方法，第二部分表示节点j单独成为一个社区的信息熵的计算方法。其中，tij表示节点j加入社区i内后，社区i中包括节点j在内的每3个节点之间能够通过边来形成的三角形的数量，如果这3个节点能够通过边形成三角形，那么表示这3个节点之间都有所联系，三角形的数量越多，代表该社区的稳定性越好，稳定性越好则代表对移动用户节点集的聚合度越明显，社区划分也更加准确。dj表示节点j的度数，s表示节点j与社区i中直接关联的节点的数量，根据信息熵理论，C是一个常数，u表示节点j可能加入其他社区的社区总数。

基于以上定义，文中提出了基于信息熵相似度的社区检测算法(CDIES)。首先计算移动节点构成的社交网络中每对节点间的相似度，并根据提前设置好的阈值δ生成带权值的无向图G=(V,E)，即相似度大于阈值δ的两个节点之间才会生成一条边，这两个节点成为邻居节点。然后计算邻居节点对之间的信息熵相似度，将信息熵相似度最小的节点对合并到同一个社区中，按照该过程一直重复循环，直到所有的节点都找到了属于自己的社区，具体的社区划分过程如下：

步骤1 对于V中所有节点v，先计算节点的相似度，生成带权无向图，然后将每一个节点加入到不同的社区，最后找出节点v的邻居节点集合，并将节点v加入到集合N。

步骤2 对集合N中的任意一个节点vi，在它的邻居节点集合中选取与vi不属于同一社区的节点vj，计算vi和vj之间的信息熵相似度，求出最小信息熵相似度，添加到集合B(vi)中，并合并到社区集合B，最后将vj从vi的N集合中删除。

步骤3 重复步骤2，直到集合N中所有节点都遍历一次，这样就得到了最终的社区划分B。

2.2 基于社区的感知任务分发算法

本研究主要利用基于概率大小的随机分发机制进行感知任务的分发，首先计算不同社区接收到感知任务的概率(简称分发概率)，具体的以不同社区中候选节点的数量占整个候选节点集的比例来对分发概率进行近似，并按照概率的大小依次对所有社区任务分发的优先级进行排序；其次将不同社区内的节点集抽象为一个无向图，并以社区中的候选节点为根节点以广度优先遍历的方式对感知任务进行携带转发并限制转发的跳数，对图的遍历深度每加深一层，则对转发的跳数减一，当跳数为零时停止任务的转发；最后，统计不同社区中所选择出的节点的数量，并以任务请求者所要招募的移动节点数量为约束进行任务的分发。任务分发的具体过程如下：

步骤1 先创建一个空集合S，在前面划分好的社区中任意取出一个社区c，将c中的一个候选节点添加到S中，计算c中的候选节点和分布概率，重复该步骤直到社区内所有节点遍历完毕。

步骤2 根据分布概率对社区集合B进行排序。

步骤3 在社区集合B中任意取出一个社区c，判断遍历深度限制δ>0，然后创建一个空集合z，对于步骤1中求出的集合S中的任意一个节点，根据深度限制δ进行广度优先遍历，并将遍历的节点加入到z，重复该步骤直到社区集合B遍历完毕。

步骤4 返回感知服务参与节点集合。

3 实验与结果分析

本研究分别在MIT RealityMining数据集[12]、Zachary空手道俱乐部数据集[13]、Lusseau海豚数据集[14]以及美国足球联盟网络数据集[15]上从3个方面评估分析了CDIES算法的准确性和有效性，并与经典的GN算法[16]、FN算法[17]进行了分析比较。

3.1 节点间社会关系度量的准确性比较

本节评估节点间社会关系度量的准确性，并设置了准确率precision、召回率recall和f1-score这3个指标来进行分析评价。

节点间社会关系分为亲密和不亲密，为了便于对上述指标进行量化比较，用TP(相似度大，实际亲密程度也高)和FN(相似度小，但实际亲密程度高)表示亲密度正相关类，用FP(相似度大，但实际亲密程度低)和TN(相似度小，实际亲密程度也低)表示亲密度负相关类。

准确率(precision)是指在相似度大的节点中，节点间亲密度高的节点所占的比例，计算公式如下：

(11)

召回率(recall)指正确的量化结果的覆盖程度，计算公式如下：

(12)

f1-score能够更好地解决准确率与召回率之间的平衡性，其计算公式如下：

(13)

文中使用流行的两种模型(基于内容的好友推荐模型Method 1，基于关系的两阶段好友推荐模型Method 2)与IQSA算法进行实验对比，这3种方法在不同好友推荐数下的precision、recall、f1-score分别如图2所示。

由图2(a)可以看出，在好友推荐数较少的情况下，这3种方法的准确率都比较低而且彼此非常接近，但是随着好友推荐数的不断增大，IQSA算法的准确率上升较快且高于其它两种推荐算法。由图2(b)可见，召回率与好友推荐数之间是成反比关系的，各种方法的召回率都会随着好友推荐数的增加而下降，这是由召回率的固有特征决定的，但IQSA算法的召回率始终高于其它两种方法。

图2 各种方法在不同好友推荐数下的准确率、召回率和f1-score

由图2(c)可见，f1-score的值在好友推荐数到达15附近时达到最优，且IQSA算法的f1-score也总是大于另外两种方法，这代表IQSA算法的综合性能是3种方法中最优的，且对节点间相似度的量化更为合理。

3.2 社区划分结果的比较

MIT RealityMining数据集包含94个节点和1 372条边，为了保证数据分析的有效性，本研究对实验数据进行了预处理，删除掉了交互记录较少和一些孤立节点,最终得到了88个节点和117条边。本节分别使用GN算法、CDIES算法对该数据进行社区划分,得到的结果如表1所示。

表1 GN算法和CDIES算法对MIT RealityMining数据集的社区划分结果

由表1可见，CDIES对社区划分的准确率相比于GN算法高出了5.582个百分点，可以更为准确地反映节点间真实的社会关系。

3.3 模块度值的比较

模块度M是评价社区划分好坏程度最常用的指标，文中定义模块度的计算公式如下：

(14)

其中：Eij表示参与式群智感知中的移动节点组成的网络的邻接矩阵的所有元素，若节点i与节点j之间有边相连，则Eij=1，否则为0；m是该无向网络中边的数量的总和；di表示节点i的度数，dj表示节点j的度数；δxy是克罗内克函数，其表达式为

(15)

特别地，M=0表示所有观察节点都被划分在同一个社区，M的值越大，则代表对移动节点集进行社区划分的结构就越清晰，社区划分的结果也越接近于现实情况。文献[16]中定义，模块度值的区间是[-0.5,1]，并在计算机生成图、Zachary空手道俱乐部和大学足球队数据集上进行了分析，结果表明，模块度的值在区间[0.3,0.7]时，社区的结构更加准确和清晰。

本研究分别在Zachary空手道俱乐部数据集、Lusseau海豚数据集与美国足球联盟数据集(记为Fatball)上计算了采用CDIES算法、GN算法与FN算法进行社区划分后的模块度，结果如图3所示。

由图3可以看出，采用CDIES算法进行社区划分后的模块度值始终是在区间[0.3,0.7]之内的，这说明随着数据的增多，CDIES算法对社区划分的结果会越来越稳定。另外，从图3中也可以看出，CDIES算法在这3个主流数据集上的模块度值始终是最大的，所以社区划分的结构相比其他两个算法更为合理与接近现实。

图3 各算法在不同数据集上进行社区划分后的模块度值

3.4 时间开销的比较

本研究从时间开销入手分析了3种算法(CDIES算法、GN算法与FN算法)在不同数据集上完成社区划分所需要的时间，如图4所示。

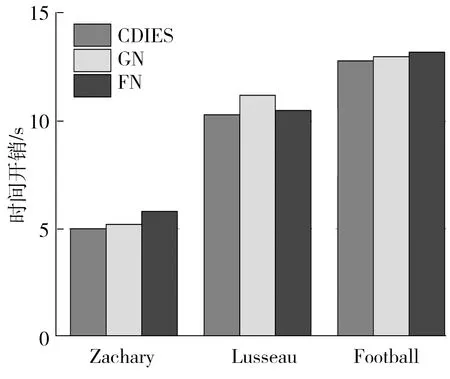
图4 CDIES算法、GN算法与FN算法在不同数据集上的时间开销

从图4中可以看出，CDIES算法在这3个数据集上的时间开销始终是少于其它两种算法，再结合社区划分结果的准确度以及模块度进行综合比较，可得，CDIES算法明显优于其它两个算法。

4 结语

本研究提出了一种基于社会关系的群智感知任务分发机制。首先根据节点间的社会关系计算出的相似度将移动节点集构成有组织有结构的网络拓扑图，然后根据该网络拓扑结构进一步进行社区划分，使得感知任务能够在不同的社区内进行分发，一方面解决了由于任务招募不到足够的移动用户带来的问题，另一方面形成了多个不同的社区，每个社区都是动态更新的和拥有持久分发链路的。