基于词嵌入与卷积神经网络的建筑能耗预测
2021-07-09季天瑶王挺韶
季天瑶 王挺韶
(华南理工大学 电力学院,广东 广州 510640)
随着“十三五”期间能源消耗总量和强度“双控”政策的出台,节能减排将继续成为我国经济社会发展中追求的目标之一。建筑能耗在能源消耗中所占比重相当大[1],因此建立精确的建筑能耗回归模型能帮助政府、开发商对建筑进行合理规划;也能协助电网合理分配能源,制定准确的日、月发电计划,达到节约能源的目的。
影响建筑能耗的因素众多,建筑元信息(包括建筑面积、建筑用途、地理位置等)以及时序信息(如气象和时间)都会影响建筑的能耗。传统的能耗预测方法与负荷预测的方法类似,主要包括线性回归(Linear Regression,LR)、支持向量机回归(Support Vector Regression,SVR)、时间序列分析[2]、集成机器学习及神经网络等基于数据驱动的方法。
由于能耗预测的数据特征过多,传统的线性回归模型不能处理大量的特征,因此线性回归模型在大规模数据集上的预测精度很难达到较高的水平。支持向量机回归不能充分利用时序特征,且在大量训练样本中的训练速度过慢。时间序列分析仅仅考虑了建筑能耗的时间特性,而没有考虑到建筑本身的特征,也会影响能耗预测的准确性。如果使用高性能的机器学习模型进行回归,如梯度决策回归树[3],虽然能利用到两种特征,但形成树的过程需要分裂大量的节点,使得模型训练过程偏慢,回归结果仍有待提升。
神经网络在回归预测中也得到了广泛应用[4],基于长短时记忆网络(Long Short-Term Memory,LSTM)的回归模型充分利用了数据的时序特性,在时序回归上有较好的效果。然而,LSTM参数难以调节,网络参数庞大,在训练过程中经常会出现梯度弥散或者梯度爆炸的现象,且模型的训练时长过长。因此构建一个性能良好的模型需要克服诸多困难。
神经网络的超参数调优往往依赖于经验,当网络规模较大时,超参数的调节会耗费大量的时间。近年来,为了减少调节超参数的时间,对超参数进行自动搜索成了当前的一个研究热点[5]。然而,随着深度学习方法的日益普及,数据量不断增大,模型复杂度也越来越高,对高效的自动超参数搜索提出了更高的要求。
建筑能耗具有时序特征,比如季节、月份、节假日、同一天不同的时间段等时序因素都会影响能源的消耗;同时,建筑能耗与建筑自身特征也存在联系,比如建筑面积、建筑用途等因素对建筑能耗也有明显的影响。因此,本研究提出一种综合考虑能耗时序特征以及建筑物自身特征的深度学习模型。首先,引入一维卷积核(Conv1D)对时序特征进行时间特征提取,引入词嵌入模型对建筑自身特征进行提取。为进一步提高模型的性能,引入基于贝叶斯优化的自动机器学习(Automated Machine Learning,Auto ML)技术对神经网络的超参数进行优化[6- 7]。由于该模型规模较大,如果直接对模型进行超参数搜索,将会大大增加超参数寻优的搜索时间。因此,本研究采用了分步的超参数自动优化方法,即在超参数的优化中,分步地对卷积网络、词嵌入层和全连接层进行超参数搜索,大大减少了超参数寻优的时间。最终,建立了一个较精准的建筑能耗预测模型,并对其泛化能力进行了验证。
1 设计方案
为了同时从分类数据中提取分类特征、从连续数据中提取时序特征,本研究采用词嵌入网络与一维卷积网络的混合神经网络,分别对分类数据和连续数据进行特征提取。
1.1 词嵌入模型
词嵌入(Word Embedding)是一种单射(f:V→S),在自然语言处理中,Embedding层可以将稀疏的词向量映射到低维且紧密的特征空间[8]。在该特征空间中的向量可以通过计算距离来度量特征间的相似性。由于特征空间是原始向量空间的特征压缩,其维度远小于原始向量空间,因此可以大大减小距离计算的复杂度,也可以避免原始特征向量过于稀疏对特征提取造成的不良影响。词嵌入模型的示意图如图1所示。
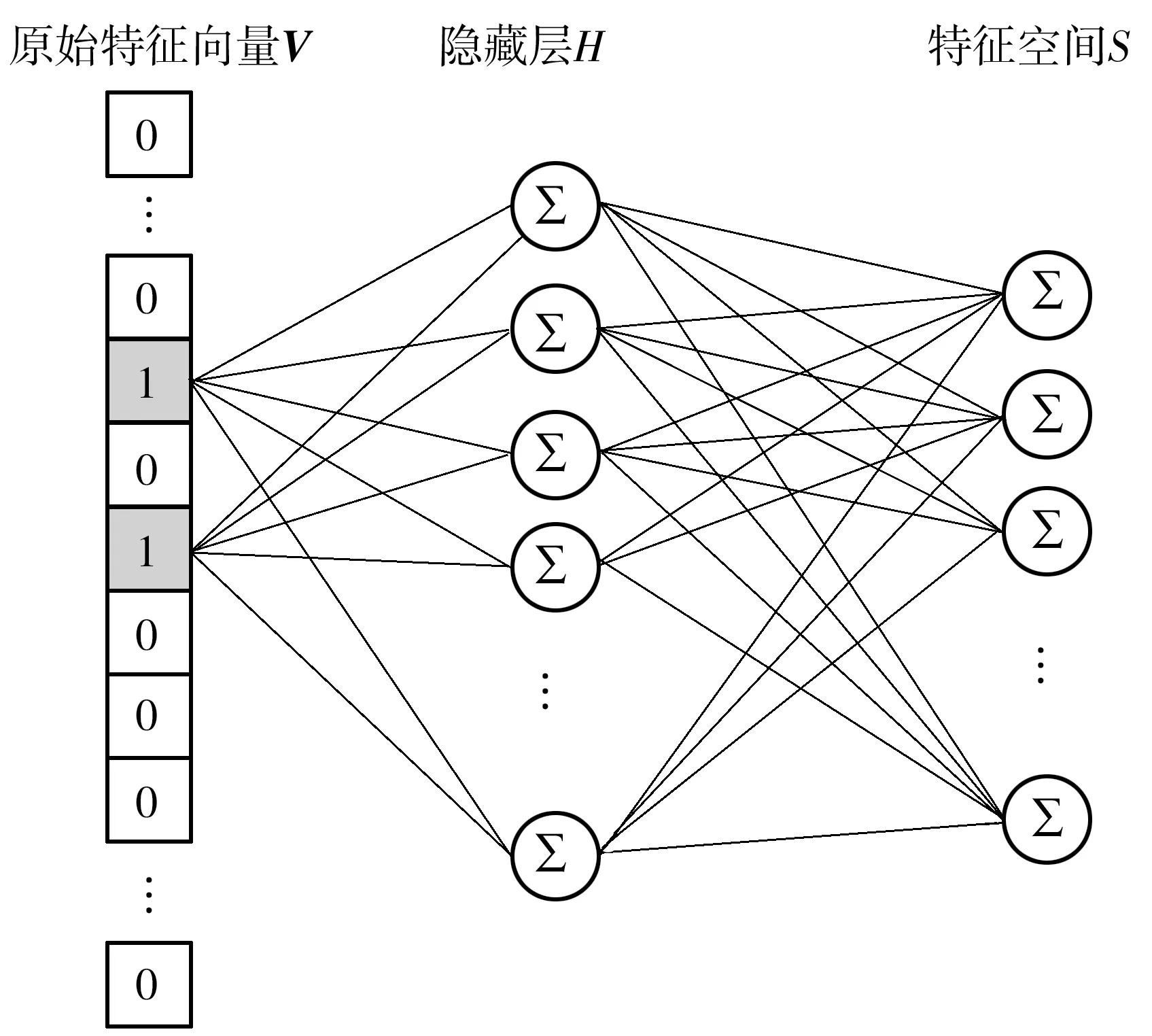
图1 词嵌入模型
在N维词向量空间V∈RN中,其特征间的关系可以用条件概率表示为
(1)
其中:vi为目标特征,vj为特征空间中的其他特征。
在神经网络中,p(vj|vi)可以表示为
(2)
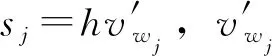
因此,在给定目标特征vi下,可以得到网络的损失函数为
(3)
由式(3)可以看出,经过词嵌入层,可以充分提取分类特征的相关性,且新的特征被嵌入到一层网络中,降低了输入数据的维度,这层网络可以作为新的输入,解决了分类特征由于独热编码导致的特征离散化以及特征维度过大的问题。
建筑元信息中存在分类特征,如建筑的用途、建筑的位置等,这些数据对建筑的能耗都有明显的影响,但不以数值形式存在,如果用独热编码对分类特征进行编码,会导致数据维度过大。为此,本研究所建立的融合神经网络引入了Embedding层,利用Embedding层对离散的分类信号进行嵌入计算,从而将离散的分类特征映射到连续的词嵌入空间,使得离散特征能和数值特征进行融合计算。同时词嵌入层减少了数据维度,降低了网络的训练时间。
1.2 一维卷积层
本研究选取卷积神经网络对数据进行回归。卷积是一种数学运算,过程是把一个张量、矩阵或向量通过卷积核的卷积运算,得到一个维度更小的包含特征信息的张量。以二维卷积核为基础的深度卷积神经网络最近几年在图像识别中取得了重大突破。然而,二维卷积核是在图像数据的长和宽两个维度上进行运算,获取的特征为二维的图像特征。考虑到时序数据的维度只有一维,本研究选取一维卷积对数据进行时序特征的提取。
一维卷积核在时间序列上对时序数据进行卷积,其运算过程如图2所示。
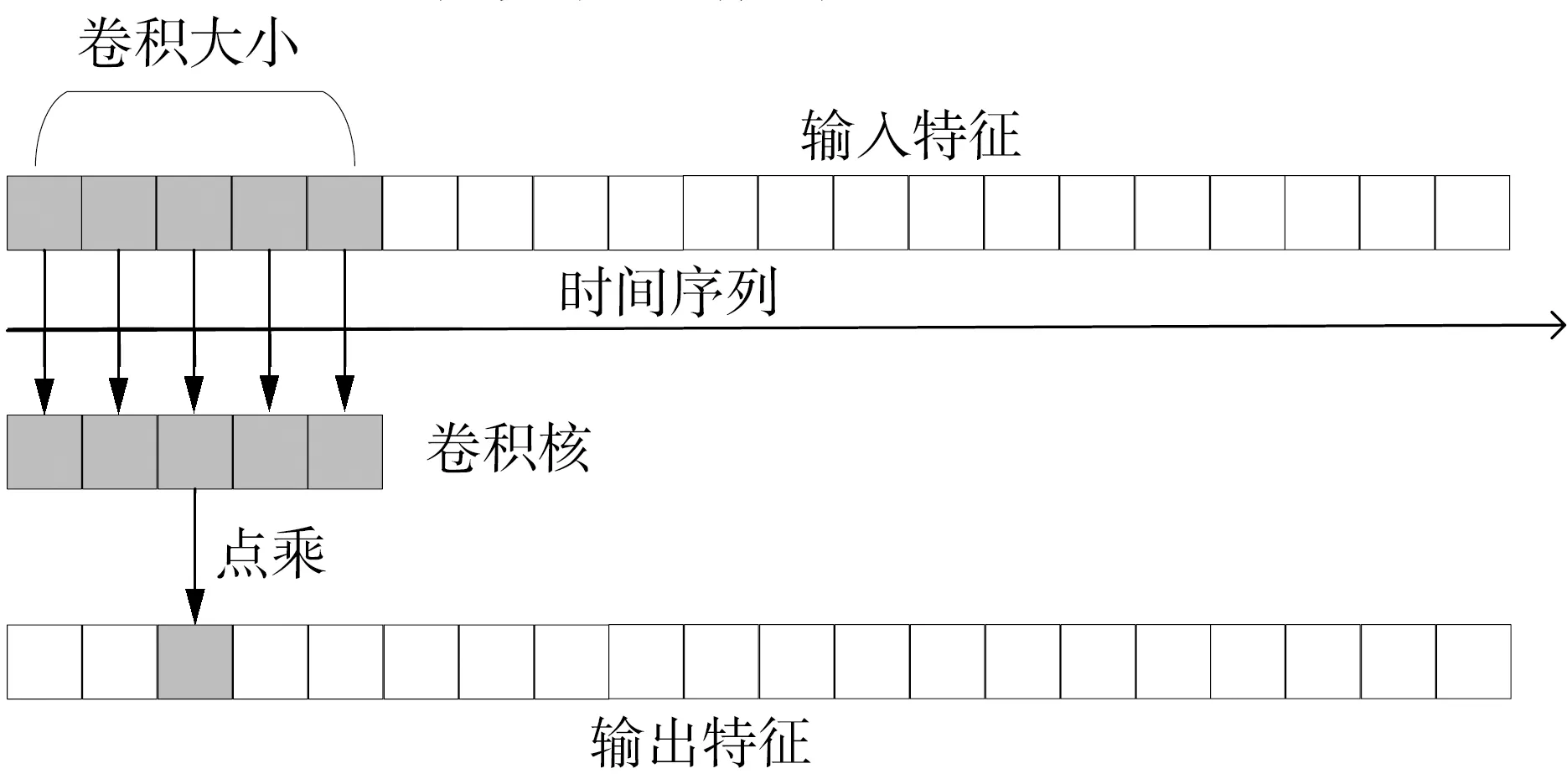
图2 一维卷积运算过程
本研究基于Embedding与一维卷积网络的特性,提出了一种基于Embedding-Conv1D的神经网络预测模型。首先使用卷积网络对时序数据进行一维卷积,通过卷积的时序特征再进入全连接层网络中进行计算,通过全连接层的特征与经过Embedding层的特征进行联接,联接后的网络再通过两层全连接层进行回归。具体的网络架构如图3所示。
1.3 基于贝叶斯优化的自动超参数优化方法
由图3可知,文中的网络模型较为复杂,对应的超参数众多,对每个超参数进行优化调节较困难。针对上述情况,本研究引入了贝叶斯超参数自动优化方法,对网络的参数进行自动调参。鉴于贝叶斯超参数优化对硬件的性能要求极高,文中提出了序列化的参数优化,使得在硬件要求不高的情况下也能实现参数自动优化。
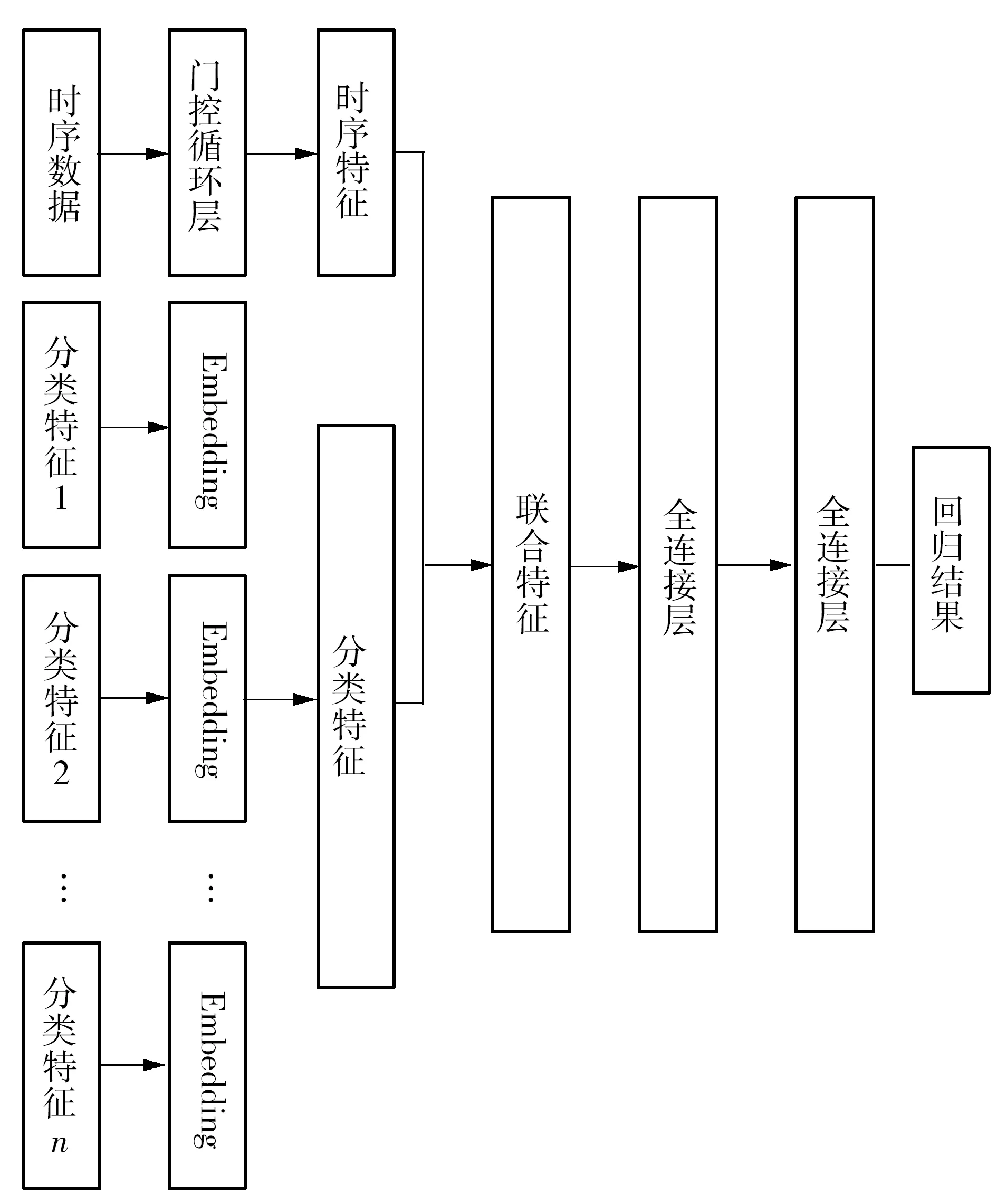
图3 Embedding-Conv1D模型
1.3.1 贝叶斯优化
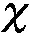
1.3.2 Tree-Structured Parzen Estimator(TPE)算法
本研究使用TPE算法[5,9]对模型的参数进行自动优化。TPE算法是一种基于模型的序列全局优化方法(Sequential Model-Based Optimization,SMBO)。常见的SMBO算法还有高斯过程期望最大化算法(Gaussian Process-Expected Improvement,GP-EI)[5]。与GP-EI方法通过高斯过程寻找最优参数的方式不同,TPE算法首先构建一个由超参数构成的图搜索空间,比如先搜索网络的层数,再搜索网络的激活函数,继而搜索网络的学习率。TPE算法的优化过程是一个在这个图搜索空间中逐层搜索的过程,这也是算法命名为Tree-Structured的原因。
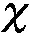
(4)
其中,l(x)是搜索空间中的x(i)使得f(x(i))小于y*的密度分布,g(x)是使f(x(i))大于y*的密度分布。
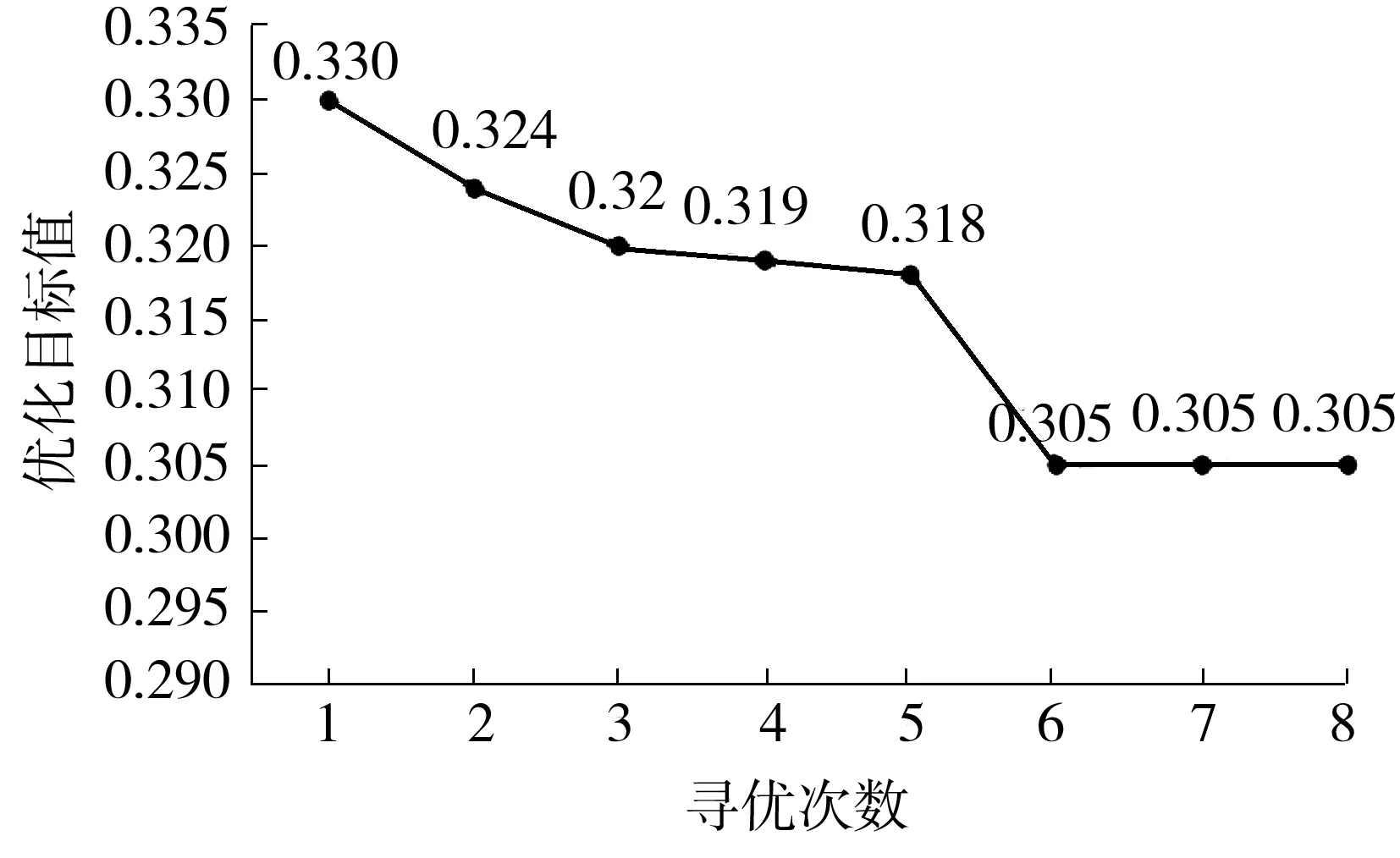
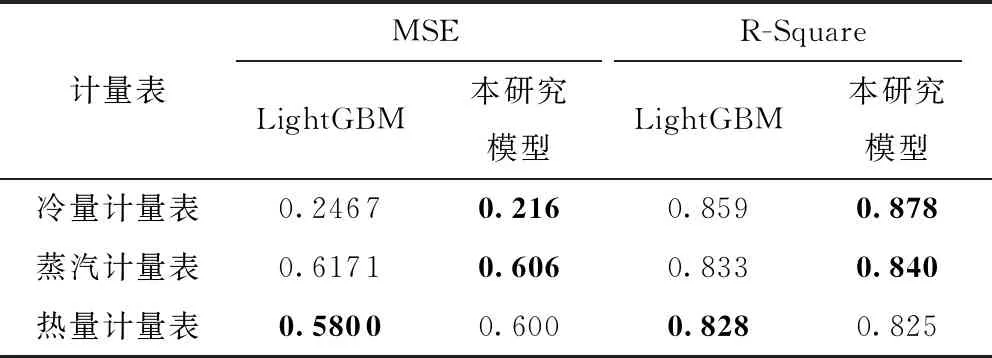
可见,获得较准确的分布的前提是对y*进行合理的设置,一般选取一个分位点γ:p(y 本研究使用期望提升算法(Expected Improvement,EI)选取最优x(i)。EI算法是基于贪婪策略的启发式算法,即在当前最佳采样点的基础上对期望改进最大的点进行采样,EI算法简单且易于实现,在实践中拥有良好的表现。TPE算法中的EI为 (5) (6) 最终可以得到 (7) 在TPE算法的具体实现中,通过Parzen估计,得到先验分布,继而由式(4)得到对应的l(x)和g(x)。最后通过求解最大期望值得到新的x*,并以此更新搜索空间。 Parzen估计需要选择窗口函数。由于在超参数空间包含离散型和连续型超参数,因此需要选用不同的窗口函数进行Parzen估计,从而得到能表征超参数类型特征的后验概率分布。对于连续变量,本研究选用截尾高斯混合模型(Truncated Gaussian Mixture Model,Truncated GMM)来拟合连续超参数的先验分布。Truncated GMM的均值为所有连续型变量均值的加权和,而分布的方差则选取相邻分布方差的最大值。 针对建筑能耗预测问题,本研究的实验流程如图4所示。实验配置环境:操作系统为Ubuntu18.04 LTS,内存为32 G,CPU为Intel Core i7-7700,GPU为Nvidia GTX-1070Ti。使用的深度学习框架为Keras,并使用TensorFlow作为Backend。具体的实验步骤如下。 图4 实验流程 步骤1 预处理数据,对缺失的天气数据进行插值,对缺失的分类数据进行剔除。分析天气数据的时间特性,确定天气特征中具有时序相关的特征。时序特征分析通过计算时序数据的自相关系数(Auto Correlation Factor,ACF)和偏相关系数(Partial Correlation Factor,PCF)来确定。通过选择合理的滞后系数k,确定合适的滑动窗口值,从而构建时序特征,将窗口内的平均值、最大/最小值、中值等统计变量作为额外的时序特征加入训练数据中; 步骤2 构建基于Embedding与一维卷积的神经网络模型,并用贝叶斯超参数优化对模型的超参数进行选择。由于网络的规模较大,本研究在实验过程中选取了分步优化的策略,即逐步地对Embedding网络和卷积网络进行优化,在综合两个网络的最优超参数后,再通过微调的手段对个别参数进行调整,最终确定整个网络的参数; 步骤3 对比验证文中模型的性能。 本研究所用数据来自ASHRAE-Great Energy Predictor Ⅲ。这是一个数据挖掘比赛[10],数据由美国建筑技术协会(ASHRAE)提供,该协会采集了不同地方不同建筑为时一年的历史数据,数据主要包含的信息包括:计量表(电表,冷量表,蒸汽表,热量表)读数;建筑元信息(如用途、投用时间、建筑层数、建筑地点)和气象信息(如空气温度、云层覆盖、露点温度、气压、风向速度)。对应地,数据中还有与训练数据集结构一样的测试数据集。 由于数据中有很多缺失值,因此需要进行预处理。对于天气数据中的缺失值,本研究选用了插值方法对缺失数据进行填充。对于建筑元信息中的分类特征,则采取剔除缺失值的方法进行处理。 考虑到气候特征具有时序特性,本研究的数据预处理将构建滚动窗口特征。在构建滚动特征之前,需要分析气候特征的时序相关性,从而确定滞后系数。因此本研究对气候信息进行了自相关系数分析。自相关系数可以定义为 (8) 其中:k为滞后系数,k=0,1,…,∀t;序列{Xt-k}是序列{Xt}滞后k个采样点后所形成的序列;Cov(Xt-k,Xt)为(Xt-k,Xt)的协方差;Var(Xt-k)、Var(Xt)分别为Xt-k和Xt的方差;如果序列{Xt}满足ρk=0,k=1,2,3,…,则可以认为{Xt}为白噪声序列,即没有时序相关性;反之,ρk越大,则说明时序相关性越大。气候信息的自相关分析结果如图5所示。 由于篇幅关系,仅展示有时间相关性的气候特征。由图5可见:温度具有明显的时间相关性,且其相关性具有明显的周期性;同时,气压与时间之间也具备相关性,且其相关性同样体现出了周期性的特征;风速和风向数据在短时间尺度上具有时间相关性。根据自相关分析的结果,考虑相关性的周期特性,选取时间窗口时应保证窗口内的时序数据的自相关性不高。为此,本研究分别添加了窗口大小为12、24、72和720 h的风速、风向、大气温度、气压滞后数据,滞后数据包括滞后时间窗内的最大值、平均值和最小值。 图5 气候特征自相关分析结果 本研究构建的模型如图3所示。对于超参数优化部分,选取Optuna[11]作为超参数优化的工具。Optuna是一个专门为机器学习的超参自动优化而设计的框架,在Optuna中可以设置优化的采样算法,如TPE采样、随机采样、高斯过程采样等。由于采用TPE算法,需要预先定义超参数的搜索空间,搜索空间设定为树型搜索空间,空间的设定如图6所示。 图6 树型结构超参数搜索空间 搜索空间的参数类型可以分为离散型和连续整数型,其中激活函数、优化器属于离散型参数,而其他参数属于连续整数型参数。超参数搜索空间的预设值见表1。 表1 超参数搜索空间的预设值 考虑到超参数寻优需要大量的运算,寻找最优参数的时间将会随着模型复杂度的增大而大幅增加。因此,本研究采取了分步优化的策略,即分别对Embedding网络与一维卷积网络进行优化,并将分别优化的结果组合起来,最后经过网络微调得到最终的网络参数。这样大大减少了寻找最优参数的时间。同时,由于计算能力有限,文中仅使用了100 000条数据作为超参数寻优的数据集。 针对模型的预测性能,文中选取了数据集中的0号计量表,即电表,进行预测实验。同时为了验证模型的泛化能力,将对其他3个计量表读数进行预测,并将结果与其他算法比对,作为验证模型泛化能力的依据。 2.4.1 对比模型的选择 为了评估文中所提模型的预测性能,选用LightGBM(Light Gradient Boosting Method)[12]、CatBoost(Categorical Boosting)、支持向量机回归和长短时记忆(LSTM)网络作为横向对比模型。LightGBM与CatBoost算法都是对梯度提升决策树(Gradient Boosting Decision Tree,GBDT)算法的改进。相比于GBDT算法每层切分特征的策略,LightGBM算法直接在树的叶子节点上进行特征切分,同时引入了直方图优化,不用对每个特征进行排序,在速度上相较于GBDT算法有很大的提升。CatBoost是另外一种改进的梯度提升算法,CatBoost能自动处理分类数据且能在GPU上并行训练,因此在精度上和速度上都有很好的表现,两种集成学习算法都在数据挖掘领域得到了广泛应用。同时,为了验证一维卷积神经网络(Conv1D)在时序上具有提取时序特征的性能,选用长短时记忆网络进行了对比。 2.4.2 实验过程与结果分析 在训练数据选择上,经过缺失值处理后的原始数据共有11 714 696条,包含时序特征27个,分类特征3个。本研究按照4∶1的比例将数据分成训练集与测试集;然而,在训练模型的过程中,笔者发现SVR与LSTM在大数据集上的训练速度过慢;因此,对于上述两个模型,本研究仅选取了其中800 000个样本作为训练模型的数据集,并同样按照4∶1的比例进行训练集与测试集的划分。 本研究选取了均方误差(Mean Square Error,MSE)、R方误差(R-Square)与模型的收敛时间作为性能评价指标。其中:MSE表征模型的准确度,MSE越小,则模型越准确;R-Square表征模型对于输出变量的解释性,R-Square越大则说明模型的解释性越强。MSE和R-Square的定义分别为 (9) (10) 本研究选取是否在本模型上使用TPE算法进行对比,同时与其他超参数搜索方法进行了对比。在不使用TPE算法时,选用网格搜索(Grid-Search,GS)算法作为超参数调节的手段。 本研究选用了早停止(Early Stopping)策略来终止训练以防止模型的过拟合。同时对于所有算法采用k-fold交叉验证,k值设置为6,最后的结果取6次的平均值。实验结果如表2所示。 表2 模型性能对比 由表2结果可知,本研究所提出的模型在准确度和模型的解释性上都具备很高的性能,仅比LightGBM算法稍低,而优于其他集成学习算法和神经网络。本研究的模型在收敛时间上耗费较多,这是超参数的搜索进行较多的迭代训练所致。 2.4.3 超参数搜索有效性验证 本研究以模型总体的均方根误差最小为超参数搜索的目标,在每次迭代搜索中,TPE算法在参数空间中寻找可能的组合,使得模型在本次迭代的均方根差比上次迭代小。TPE算法的搜索结果如图7所示。 图7 TPE算法迭代搜索过程 由图7可以看出,TPE算法能有效对超参数进行搜索。在前6次迭代中,通过超参数的寻找,模型的均方根误差逐次下降。但由于TPE算法并不是稳定的搜索过程,模型性能会出现一定的波动,因此需要进行一定的剪枝,在模型性能无法得到进一步提高时停止迭代。 在图7搜索的过程中,模型最终的均方根误差为0.305,这与表2中的结果有一定差别。这是由于图7的搜索过程仅为卷积层的搜索,词嵌入层的超参数仍需再进行一次超参数搜索。最后在获得两者的超参数的基础上进行微调,从而得到总模型的最终参数。由于对模型的总体寻优将会耗费十分多的计算资源,导致寻优过程偏慢,本研究分步对两个子网络进行优化,所耗费的时间明显减少。 综合分析表2和图7,在加入词嵌入层后模型的均方根误差相比图7得到明显地降低,也证明了词嵌入层对于提高模型的预测能力具有显著的作用。 2.4.4 模型泛化能力验证 为了验证模型的泛化能力,文中对其他3个计量表分别进行回归预测,并采用LightGBM算法与本研究提出的模型进行对比。在LightGBM算法中,参数的设置与电表预测的参数一致。对于本研究模型的参数,仍然以用电量预测模型的参数作为参数设置的依据,没有使用TPE算法对超参数进行寻优。实验结果如表3所示。 由表3可见,本研究提出的模型的性能接近甚至优于LightGBM算法。由此可见,本研究所提出的模型具有较好的泛化能力,不仅适用于对建筑耗电量进行预测,在对建筑冷量、热量等能耗进行预测时也能得到很好的结果。 表3 模型泛化能力验证 文中提出了一种基于一维卷积与词嵌入融合的新型神经网络架构,基于该架构建立了建筑能耗短期预测模型;并通过实验对模型进行了验证。结果表明,词嵌入层和一维卷积层能分别提取离散特征和连续特征,该模型在能耗预测问题上取得良好的效果。也适用于对包含连续变量和离散变量的数据集进行回归预测。同时,本研究采用了超参数优化方法,引入贝叶斯优化算法对网络的超参数进行自动优化,很大程度上提升了模型的性能。虽然本研究的模型在精度和模型解释性上稍弱于目前最先进的LightGBM算法,但是在模型的泛化性上取得了比LightGBM更好的效果。 本研究的模型仍存在许多不足,由于分类信息只有3类,因此无法得到本模型的分类特征对预测的精度有大幅提升的结论。同时本研究在数据预处理阶段加入了许多时序特征,然而每一种计量表的时序特性不同,如果要得到精确的结果,则需要对时序数据进行分析,大大增加了工作量,获得较高拟合结果的同时,也导致了模型的泛化性不够强。因此后续研究将关注于如何在没有人为增加时序特征下,得到精准的预测值,提高模型的泛化性能。 此外,在超参数优化搜索上,虽然本研究采用了分步搜索的策略,减少了寻找参数的时间,但分步优化策略无法充分考虑不同网络其参数之间的联系,导致搜索结果无法进一步优化,在准确度上也稍劣于先进的集成学习算法,且搜索速度在单机显卡上仍然有待提高;因此,后续研究将关注于搜索策略的优化、自动搜索效率的提高与准确度的提升。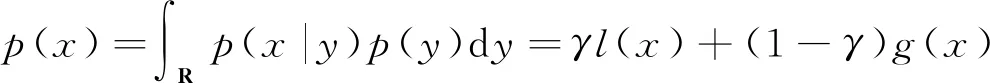
2 实验过程与模型验证
2.1 实验设计
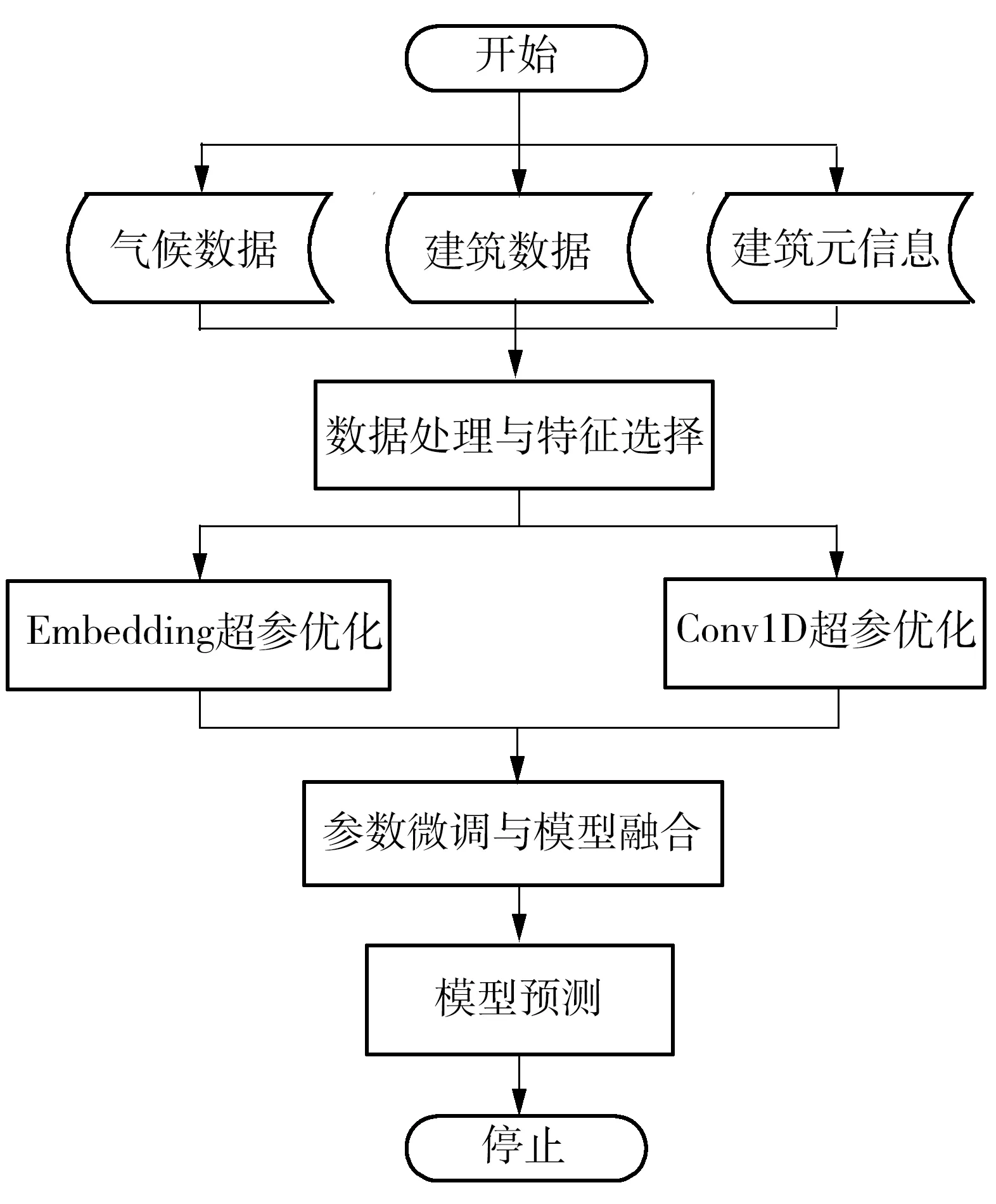
2.2 数据预处理
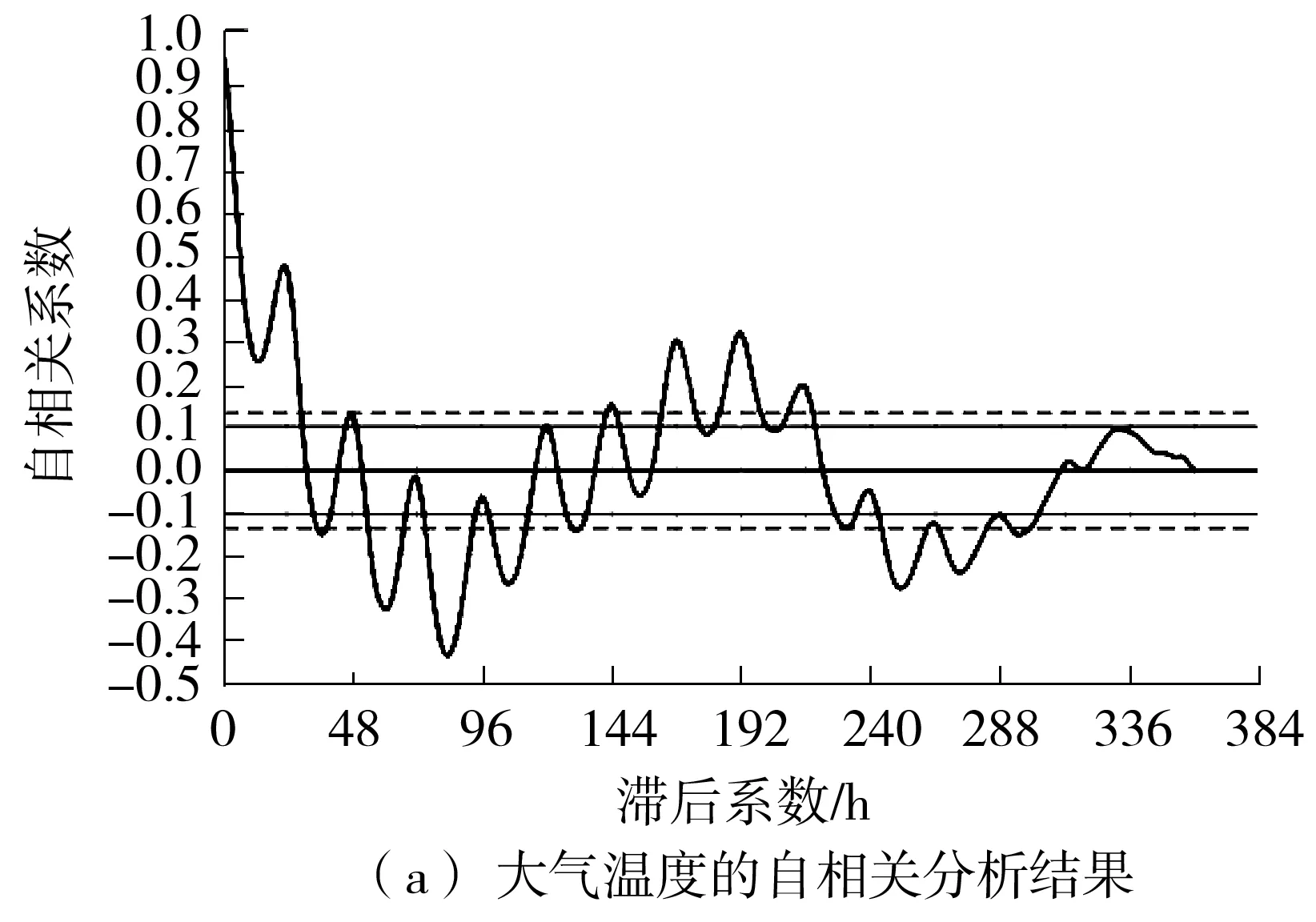
2.3 模型构建与超参数调优
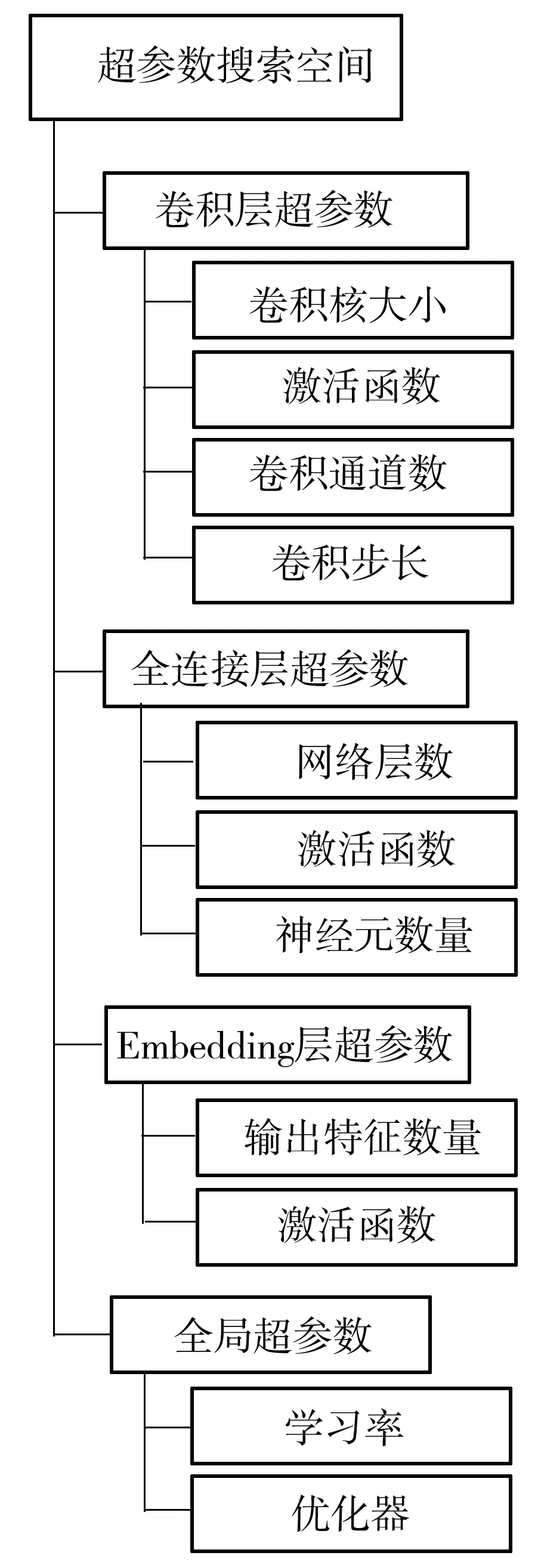
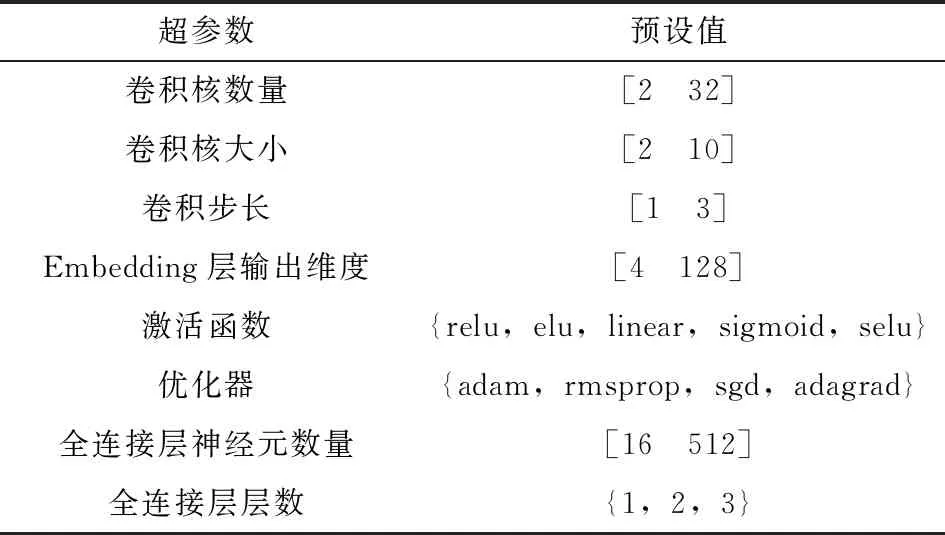
2.4 模型性能评估
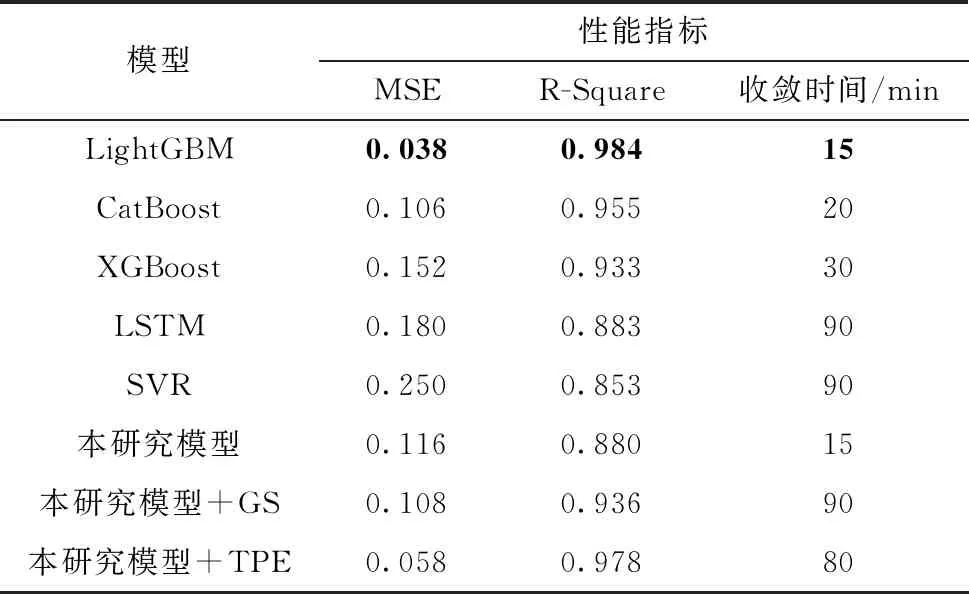
3 结语
