角单元对薄壁管耐撞性的影响

刘旺玉 田鹏飞 金林 罗远强

(华南理工大学 机械与汽车工程学院,广东 广州 510640)

汽车耐撞性问题是汽车被动安全所需解决的重要问题。薄壁结构因其低质量和卓越的能量吸收特性等优点,被广泛应用在车身耐撞性结构设计中[1]。截面形状是影响薄壁结构耐撞性的重要因素。其中,简单截面形状(例如三角形[2]、方形[3]、六边形[4]、八边形[5]和圆形[6])和由简单截面形状转化而来的复杂形状(例如星形[7]、正弦波纹形[8]和十字形[9])都被广泛研究。以上研究表明，塑性变形主要发生在管的角单元附近,角单元吸收了大量的能量。

Wierzbicki等[10]提出超折叠单元理论来解释轴向碰撞过程中移动塑性铰的形成。超折叠单元理论将变形模式分为非延展模式和延展模式。Chen等[11]在此基础上推导出简化超折叠单元理论。Zhang、Tran等[12- 14]利用简化超折叠单元理论分别对多胞方管、三板管和多胞三角形管进行了研究。他们将管截面划分为不同的基础角单元,通过叠加不同角单元对平均力的贡献得到整个管的平均力理论表达式。

根据理论可得方管的平均力为

Pm=13.10σ0C1/3t5/3,

式中，σ0是材料的流动应力,C和t分别代表薄壁管的宽度和厚度。

对于六边形管,其平均力为

Pm=30.90σ0C1/3t5/3。

因此,方管和六边形管每个角单元的平均力分别是3.27σ0C1/3t5/3和5.15σ0C1/3t5/3,意味着当角单元从90°增大到120°时,平均力增大57.5%。然而平均力随着角单元的增大而增大的结论是以几个特殊正多边形角单元(90°,108°和120°)的平均力为依据,这些角度以外的其他角度是否具有相同的影响规律无法得到验证,所以以上结论不具有普遍性。

Zhang等[15]指出边数为奇数的正多边形管会发生混合变形,即有的角单元会发生延展变形,有的角单元会发生非延展变形;而边数为偶数的正多边形每个角单元均发生延展变形。当对比90°角单元和108°角单元的平均力时会发现,方管和五边形管有不同的变形模式,而且五边形管的不同角单元有不同的变形模式,无法根据总平均力分解出每个角单元的贡献,所以传统的通过比较不同正多边形角单元的平均力来研究角单元对耐撞性影响的方法是存在缺陷的。

针对以上问题,本研究将凹角引入截面形状设计中,提出了一种凹角管,将角单元大小作为形状演变的自变量,研究轴向冲击下薄壁管的耐撞性,以此来研究角单元对耐撞性的影响,研究结果可以为能量吸收结构的设计提供参考。

1 材料与方法

1.1 几何构形

针对不同正多边形有不同变形模式的问题,新截面的设计目标首先是保证当角单元在一定范围内自由变化时,薄壁管的变形模式不发生改变。传统的正多边形管明显不满足以上要求。受Liu等[7]设计的星形管启发,本研究提出一种凹角管,这种凹角管可以突破传统多边形管对于角度的限制,并且满足以上要求。设新设计的截面是N边形,有N个内角。关于直角单元对平均力的影响已有广泛研究[10,14- 15],令N/2个内角为直角,因为任意相加为360°的两个角单元拥有相同的变形模式。因此使剩下的N/2个内角两两相加为360°,则该N/2个内角就有相同的变形模式。以上思路可以用下式表示:

(1)

求解式(1)可得N等于8。

根据设计目标生成的凹角管的几何模型和截面形状如图1所示。4个角单元顶点(A、B、C和D)都在角平分线上,且离中心点距离为30 mm;4个角单元顶点固定,4个角单元角度始终保持90°;角单元的两边绕顶点旋转可以生成不同的角。由于几何形状限制,凹角管的角度范围在90°到180°之间。角单元角度可以是90°到180°之间的任意角度,而且在角单元变化时,4个直角变形模式保持不变,所以可以认为是4个变化的角单元造成耐撞性的改变,从而实现研究角单元对耐撞性影响的目标。图中L是管高,t是壁厚,θ是角单元角度。

1.2 耐撞性指标

通过总吸能量、比吸能量、最大冲击力和平均力来定量评估和比较薄壁管的耐撞性。

总吸能量(EA)指在碰撞过程中吸收的总能量,其表达式如下：

(2)

式中，F(x)是瞬时冲击力,d是压缩距离。

为了比较不同结构的吸能能力,质量也被当作评价耐撞性的指标。比吸能量(SEA)指单位质量吸收的能量,表达式如下：

(3)

式中，M是结构的总质量。

比吸能量越大,单位质量吸收的能量越多,耐撞性越好。

最大冲击力(Fmax)指碰撞过程中的最大冲击力。如果Fmax过大会对驾驶员造成伤害,所以在吸能结构设计过程中要降低Fmax。

平均力(Fm)指整个碰撞过程冲击力的平均值,被认为是单位距离吸收的能量，其表达式如下：

(4)

1.3 有限元模型及验证

1.3.1 材料属性

实验所用材料是铝合金6061T4。基于ASTM E8M—2004的金属材料拉伸实验标准方法,对试样进行拉伸实验,获得其应力-应变曲线。铝合金6061T4的密度ρ=2 700 kg/m3，杨氏模量E=70 GPa，泊松比ν=0.3，屈服应力为112.36 MPa，极限应力为214.16 MPa处理后得到的真实应力-应变曲线如图2所示。

1.3.2 有限元模型

整个凹角管压缩模型如图3(a)所示,模型包括移动刚体、凹角管和固定刚体。移动刚体被赋予质量,以5 mm/s的固定速度冲击凹角管。有限元模型采用ABAQUS/Explicit进行数值仿真,为保证收敛,沿厚度方向采用5个积分点,凹角管底部与固定刚体绑定,并约束固定刚体6个自由度。移动刚体与凹角管之间采用面面接触,摩擦系数取0.3[8]。网格单元长度采用1 mm×1 mm。由于铝合金对应变率不敏感,数值仿真中不考虑应变率的影响。

1.3.3 有限元模型验证

为了检验有限元模型的可靠性,利用万能实验机对凹角管进行准静态压缩实验。通过线切割技术制造θ=120°的凹角管,其它几何参数同图1。万能实验机压头加载速度为5 mm/s。

凹角管准静态压缩实验、有限元模型仿真的变形结果和力-位移曲线如图3所示。

图3 准静态压缩实验和仿真变形结果及力-位移曲线

由图3所示的最终压缩变形结果可见,尽管存在断裂,但是整体来说,有限元模型和实验有相同的变形模式和相同的褶皱数量。根据图3所示的实验和有限元模型仿真的力-位移曲线，经计算,当压缩位移达到50 mm时,试验的总吸能量EA为1 470.83 J,有限元仿真的EA为1 434.14 J,两者相差2.5%,在误差允许的范围内。除了实验时发生断裂导致第二个峰未能完整生成外,实验和有限元模型的力-位移曲线基本一致,有相同的峰数,在相近的位置变形,所以可以认为有限元模型能很好地反映实验结果,具有可靠性。

2 薄壁管参数分析

根据设计目标,θ可以取90°～180°之间的任何角度,为了研究角单元对薄壁管耐撞性的影响,角单元角度从90°开始以10°为梯度逐级增大到180°,得到10个不同截面形状的薄壁管,截面如图4所示。对10个薄壁管进行轴向冲击仿真,为模拟汽车碰撞过程,冲击刚体速度设为10 m/s,其他参数不变。

图4 不同角单元时薄壁管的截面形状

2.1 薄壁管变形模式

变形模式对薄壁管的吸能性能影响显著。图5所示为不同截面形状薄壁管的最终变形。

由图5可见，当θ从90°增大到180°时,总共有4种不同的最终变形。当θ在100°到150°之间时,为凹角管,生成3个褶皱；下面以θ=120°为例详细解释其变形,如图6所示。

图5 不同薄壁管的最终变形

由图6可见，4个直角单元以非延展模式变形,剩下的角单元以延展模式变形。因为凹角管截面形状是对称的,对称轴两边有相同的变形,在对称轴上的4个角单元以对称的延展模式变形,因为角度大于90°,长轴上的2个角单元只能向管外变形,短轴上的角单元只能向管内变形。直角单元一边向外变形,另一边向内变形,导致角单元只能以非延展模式变形,4个直角单元的变形可以看作是对称轴上4个角单元变形的结果。

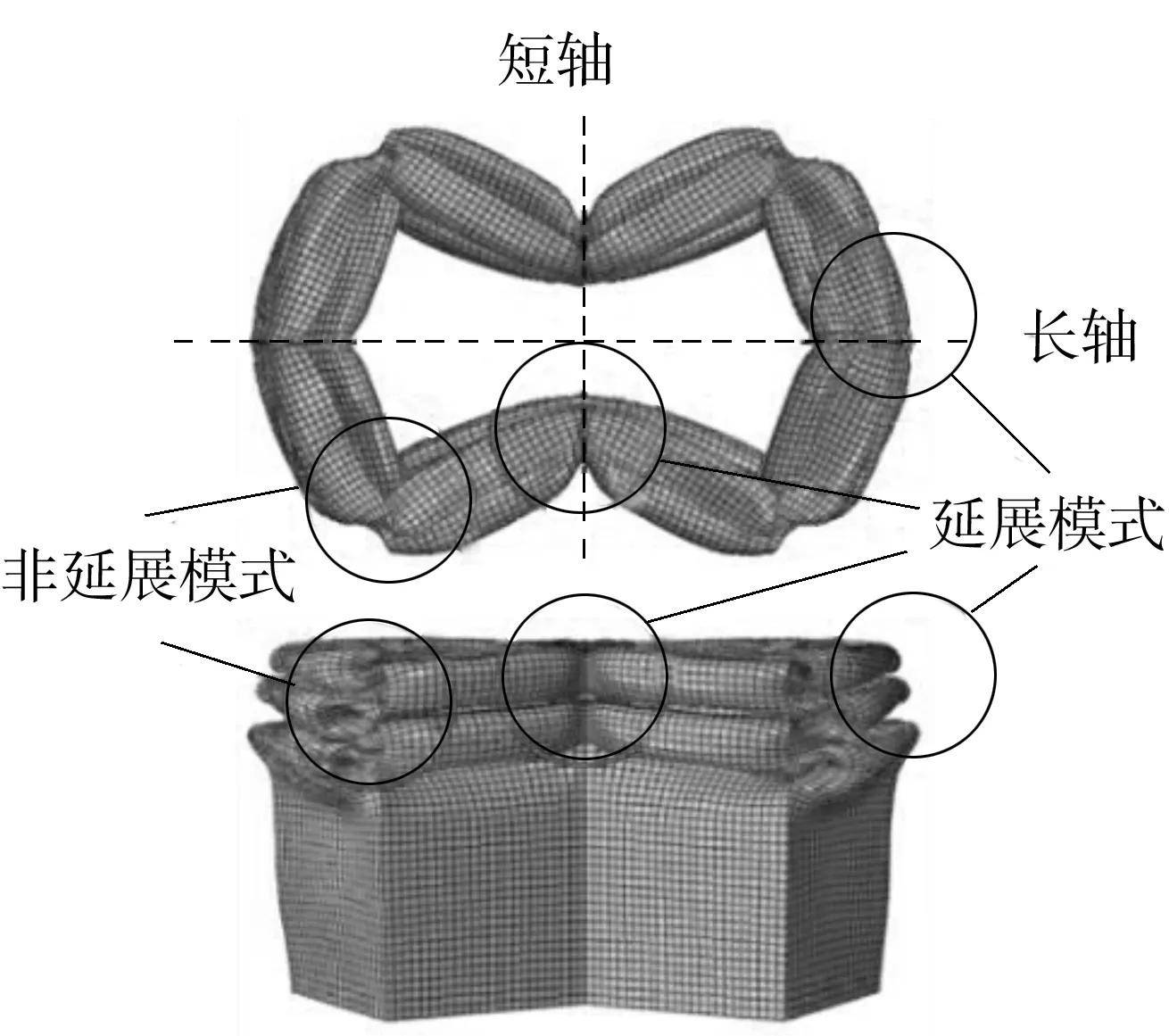
图6 θ=120°时凹角管的变形模式

当θ在160°到170°之间时,凹角管趋于发生不稳定的膨胀和收缩变形,通常有更长的波长,导致凹角管只生成2条褶皱,能量吸收效率显著降低。当θ=180°时,对称轴上角单元变为直线,形成方管,由于没有对称轴上角单元的约束,4个直角单元变形变成延展模式。当θ=90°时,实质变为多胞管。因为角度变为90°,为了吸能最大,短轴上角单元的两边向管外变形,原先4个直角单元变形变为延展模式。

2.2 角单元对耐撞性指标的影响

文中薄壁管有8个角单元,当θ改变时,4个直角单元保持不变,剩下的4个角单元同时改变,有相同的变形,所以薄壁管的耐撞性改变是角单元改变的结果。为了定量研究薄壁管的耐撞性,每个薄壁管设置相同的压缩距离用来计算各项耐撞性指标，结果如图7所示。

由图7可知，角单元对薄壁管冲击响应有重要的影响。当θ=90°,正如前人的结论[12],多胞管表现出良好的吸能特性,相对于100°凹角管,EA提高23.16%，SEA提高13.63%,不过Fmax也提高了9.28%。当θ在90°和180°之间时,Fm和EA随着角单元角度增加而减小,特别是当θ大于150°,下降的幅度增加。100°凹角管相对于170°凹角管,Fm和EA分别减少45.64%和46.84%。因为变形模式会变为不稳定的膨胀和收缩模式,导致波长增长,变形不充分,吸能效率降低。当考虑质量时,薄壁管质量随角度增加而减小,SEA呈现先缓慢增加后快速减小的变化趋势；在140°达到峰值,140°同时也是能否稳定变形的分界线。Fmax随角单元角度增加而降低,100°凹角管相对于170°凹角管降低了33.10%。当θ=180°时,方管变为延展变形模式,各个耐撞性指标相对于170°凹角管都得到提升。

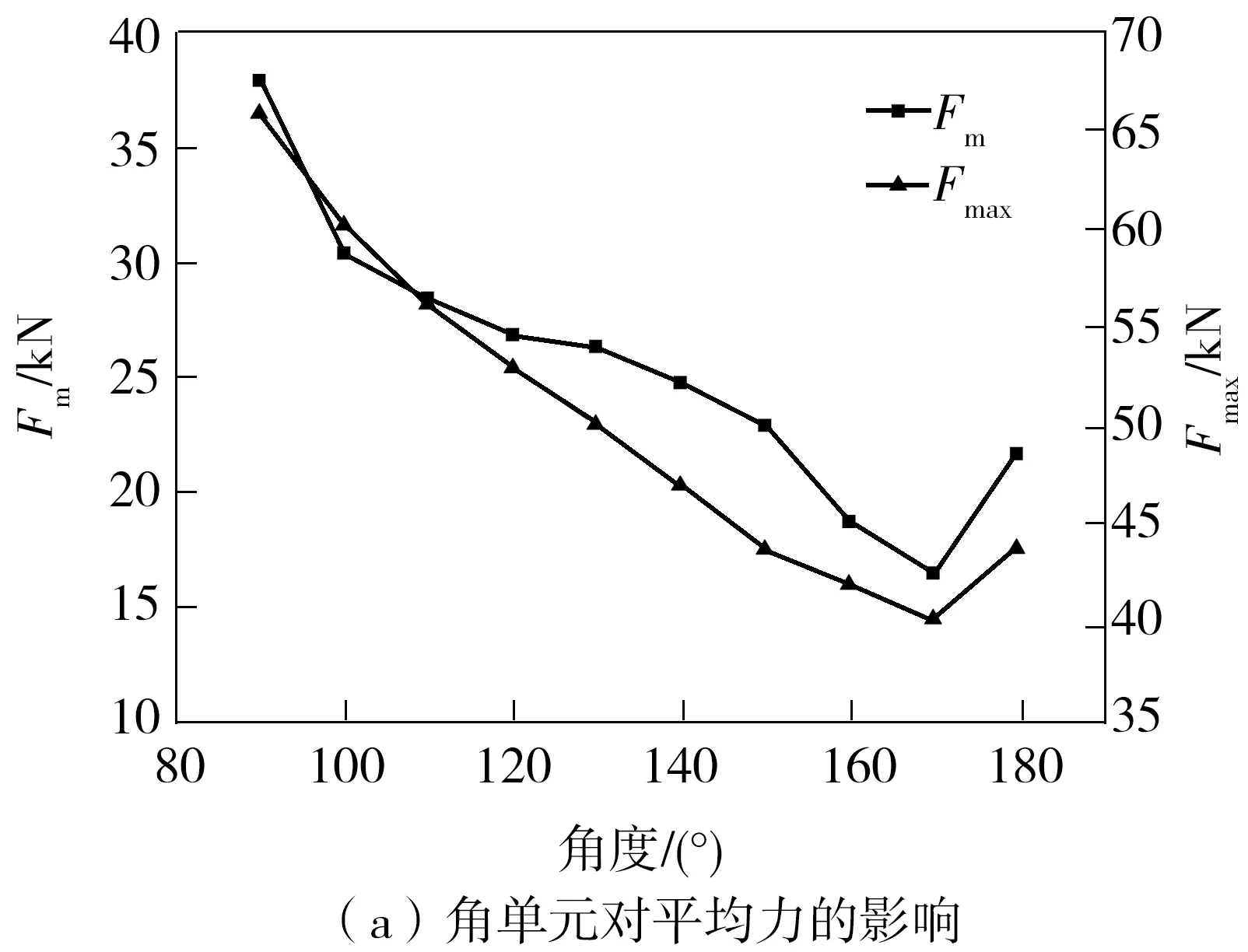
图7 角单元对耐撞性指标的影响

综上所述，管整体的最终变形决定凹角管的耐撞性，而每个角单元夹角的大小影响角单元的折叠变形模式，进而影响整个管的最终变形。90°角单元由于可以按照有利于吸能的原则调整变形方向，向最大吸能方向变形，因此被广泛应用在多胞管和多角管中；而过大的角单元角度会导致不充分变形，降低碰撞吸能效率。90°到140°之间能保证正常变形，而且耐撞性良好，为合适的角度设计范围。

3 理论预测与验证

前文已经定性解释角单元和耐撞性的关系,接下来利用超折叠单元理论定量推导出角单元与薄壁管轴向冲击平均力的表达式。基于系统能量守恒原理,来自压缩的外力做功和形成褶皱所消耗的弯曲变形能和薄膜变形能的集合相等[11]。表达式为

(5)

其中：2H、M0、B和t分别代表波长、完全塑性弯矩、截面周长和厚度;η是有效冲击位移系数,取值通常在0.7～0.75之间[3];N为整个角数的一半。

得到凹角管的平均力表达式为

(6)

根据Hanssen等[16]的研究结果可得,动态冲击的放大系数为

(7)

(8)

数值仿真和理论预测结果如表1所示。由表1可见，当θ在90°和150°之间时,数值仿真结果和理论预测结果的相对误差在5%以内,处于可接受的范围。当θ在160°到180°之间时,理论预测明显高于数值仿真结果。正如在前文变形模式中提到的,在实际变形中,凹角管在160°到180°之间时趋于按非稳定膨胀和收缩模式变形,变形不充分,导致能量吸收效率降低,因此数值仿真普遍低于理论预测。当θ=90°和θ=180°时,因为角单元变形模式发生改变,平均力公式变为

表1 理论预测和数值仿真结果的比较

(8)

修正后的数值平均力与理论平均力的相对误差也在5%以内,证明了理论平均力的可靠性。综上所述,平均力随着角单元的增加而降低。

4 结论

文中,凹角管有相同的边数,而且在轴向冲击下有相似的变形模式,被用来解决正多边形边数不同和奇偶边变形模式不同的问题,从而使角单元成为影响耐撞性的唯一指标。首先，对一系列不同角度的薄壁管进行了轴向碰撞仿真；然后，利用超折叠单元理论定量推导出角单元与薄壁管轴向冲击平均力的表达式；最后，对理论预测结果和数值仿真结果进行了对比。得到以下主要结论：

(1)当角单元角度为90°时,薄壁管可调整变形模式向吸能最大方向变形,有良好的耐撞性。

(2)当角单元角度大于90°时,EA随角度的增加而减少;SEA随角度的增加先缓慢增加,当角度超过140°,因为变形模式的改变,SEA又快速减少。

(3)当角单元角度在150°到180°之间时,不充分的变形会导致平均力仿真结果小于理论预测,而且SEA、EA和Fm均迅速下降。