高维生物医学数据变量筛选方法的模拟研究

王静娴，赵 芃，李业棉，杨嵛惠，陈方尧

(西安交通大学医学部公共卫生学院流行病与卫生统计学系，陕西西安 710061)

近年来，随着生物医学检验检测技术的发展，研究中生物医学数据的积累呈现指数级别的增长，尤其是在组学研究领域，测序技术的发展实现了基因、蛋白质等大规模组学数据的测量和积累。常规的统计分析中，在进行多变量分析时，往往要求自变量的数量和样本量成一定的比例[1]。然而，在实际研究中，特别是涉及组学分析的相关研究中，研究所关注的自变量数量往往远大于其收集的样本量数量，这类自变量的数量p远大于样本量n，即p>>n的数据被称为高维数据[2]。目前，高维数据分析被广泛应用于生物医学研究的各个领域，如计算生物学研究、组学研究、危险因素筛选和预后模型建立等。如何从海量的高维数据中提取有用的信息，筛选出最关键的研究变量，是高维数据分析研究中的重点和热点问题。

由于在高维数据的分析中存在许多假定条件，且高维数据本身的统计性质复杂，因此，在高维数据的分析中，虽然存在许多可选方法，但对于各个方法的实际效果，并没有公认的一致评价。本研究旨在通过Monte Carlo 模拟的方法，评估几种常用方法在高维数据变量筛选中的效果，为制定特定条件下高维生物医学数据的变量筛选策略提供依据。

1 材料与方法

常规的统计建模方法中，常要求数据中的变量数量(成一定比例的)小于样本量数量，且自变量间不存在或仅存在很弱的相关性。但是，这样的要求对于高维数据的建模分析来说，通常是无法满足的。因此，针对高维数据进行建模分析时，首先需要对数据进行降维，即变量筛选。为了解决这一问题，研究人员开发出了一系列方法，其中最为常见的方法包括以下这5种：

1.1 偏最小二乘法偏最小二乘法(partial least square, PLS)是高维数据降维分析中常用的方法之一，是常规的最小二乘法(ordinary least square, OLS)的一种扩展[3]。和OLS不同的是，PLS方法采用了主成分分析(principal component analysis, PCA)的方法从自变量空间中提取出主成分然后进行系数估计。由于在运算中采用了主成分分析的方法，因此，PLS方法可以很好地容忍高维变量间可能存在的多重共线性问题。

1.2 LASSO算法LASSO(least absolute square selection operator)是一种基于正则化(regularization)的高维数据变量筛选方法，它是由TIBSHIRANI[4]提出的。其基本思想是在最小二乘法的基础上施加了一个L1范数的惩罚项，实现稀疏化，来限制参数的个数：

1.3 Ridge算法岭回归(ridge regression)或Ridge算法也可以看作是最小二乘估计法的一种改进，且得到的回归系数的标准差也比最小二乘估计的要小。其基本做法是在最小二乘法的基础上施加了一个L2范数的惩罚项，基本思想与LASSO方法类似，也是基于正则化思想的一种方法[5]。当自变量中存在较为显著的多重相关关系时，它可以通过对回归系数的控制，达到减小误差的目的。其基本模型假设可以表示为：

1.4 弹性网ZOU和HASTIE[6]将Ridge算法和LASSO方法相结合，提出了弹性网(elastic net，EN)方法。其基本思想可表示为：

其中，λ1和λ2是模型中的两个非负惩罚参数，且有λ1+λ2=1。可以看出，当λ1=0时，EN方法模型退化为岭回归；反之，当λ2=0时，此退化为LASSO模型。因此，EN方法可以看做是LASSO和岭回归两种方法的结合，兼有二者的性质[7]。

1.5 自适应LASSO自适应LASSO方法(adaptive LASSO, ALASSO)是在LASSO方法的基础上发展出来的一种算法[8]。在基于高维数据的变量筛选中，该方法首先通过使用LASSO方法，在一定的模型框架下，获得变量系数的初始估计，再通过对惩罚项进行修正，达到压缩参数个数的目的。它可以看作是在LASSO方法的基础上对L1惩罚项的每一个系数进行了加权处理，对于一般的线性回归，该方法可表示为：

2 模拟研究

本研究将通过模拟研究比较几种不同的高维数据变量筛选方法在应用中的效果。

2.1 模拟方法与参数设置模拟研究基于R语言及Rstudio编程实现，模拟研究所用的高维数据基于Monte Carlo方法产生，假设变量服从广义线性回归模型：

P(y|X)=logit(βX+ε)

其中y为二分类结局变量，ε～N(0,1)为误差项。X为服从多元正态分布的自变量矩阵，维数为n×p，其中，n为样本量，p为自变量数。y为连续性应变量。

考虑到高维数据分析实践的特点，模拟研究中考虑两种自变量间的相关性情况：①自变量间均线性无关的情况；②存在一定的线性相关性的情况，设ρ|i - j|=0.5表示任意两个自变量Xi与Xj之间的相关系数；自变量间的相关性通过方差协方差矩阵控制。

模拟研究考虑的参数包括样本量(n)、自变量数量(p)，且有p>>n；变量系数假定β={β1,β0}，其中，β1=(0.2,0.5,0.8,1.1,1.4)5为X1～X5的系数，β0=(0,…,0)p-5为X6～Xp的系数。模拟研究样本量取40、80、120和160；样本量与自变量数量的比值n∶p=1∶2～1∶4。每一个参数组合下，进行1 000次模拟。

模拟评价采用真阳性率(true positive rate, TPR)和真阴性率(true negative rate, TNR)进行评价。其中，真阳性率指实际相关的变量被筛选出的概率，真阴性率指实际无关的变量在变量筛选中被排除的概率，二者的定义如下：

理想状态下，两个指标均为越接近1(100%)越好。

本研究中所涉及的5种变量筛选方法分别基于R包“msgps”(version 1.3.1)，“glmnet”(version 4.1)和“plsVarSel”(version 0.9.6)实现。其R代码如下：

#偏最小二乘法：

pls_v=rep_pls(y, X, N=SS)

pls_vs=pls_v$rep.selection

sig=matrix(0,SS+1,1)

sig[pls_vs,]=1

coef_pls[,i]=sig

#LASSO方法：

Gla=cv.glmnet(X, y, alpha=1)

coef_tepm_ri=coef(gla$glmnet.fit,s=gla

$lambda.min)

fit2=attributes(coef_tepm_ri)

coef_la[,i]=fit2$x

#Ridge方法：

gri=cv.glmnet(X, y, alpha =0)

coef_tepm_ri=coef(gla$glmnet.fit,s=gla

$lambda.min)

fit3=attributes(coef_tepm_ri)

coef_ri[,i]=fit3$x

#弹性网方法：

fit4=msgps(X, y, penalty="enet",alpha=0.5)

coef_en[,i]=coef(fit2,2.5)

#ALASSO方法

fit5=msgps(X, y, penalty="alasso",gamma=1)

coef_al[,i]=coef(fit5,2.5)

2.2 模拟结果

2.2.1变量间线性独立条件下的筛选结果 第一部分模拟研中假设自变量间的相关系数均为0，即在变量间线性独立的条件下进行变量筛选，5种筛选方法的效果如下表1所示：

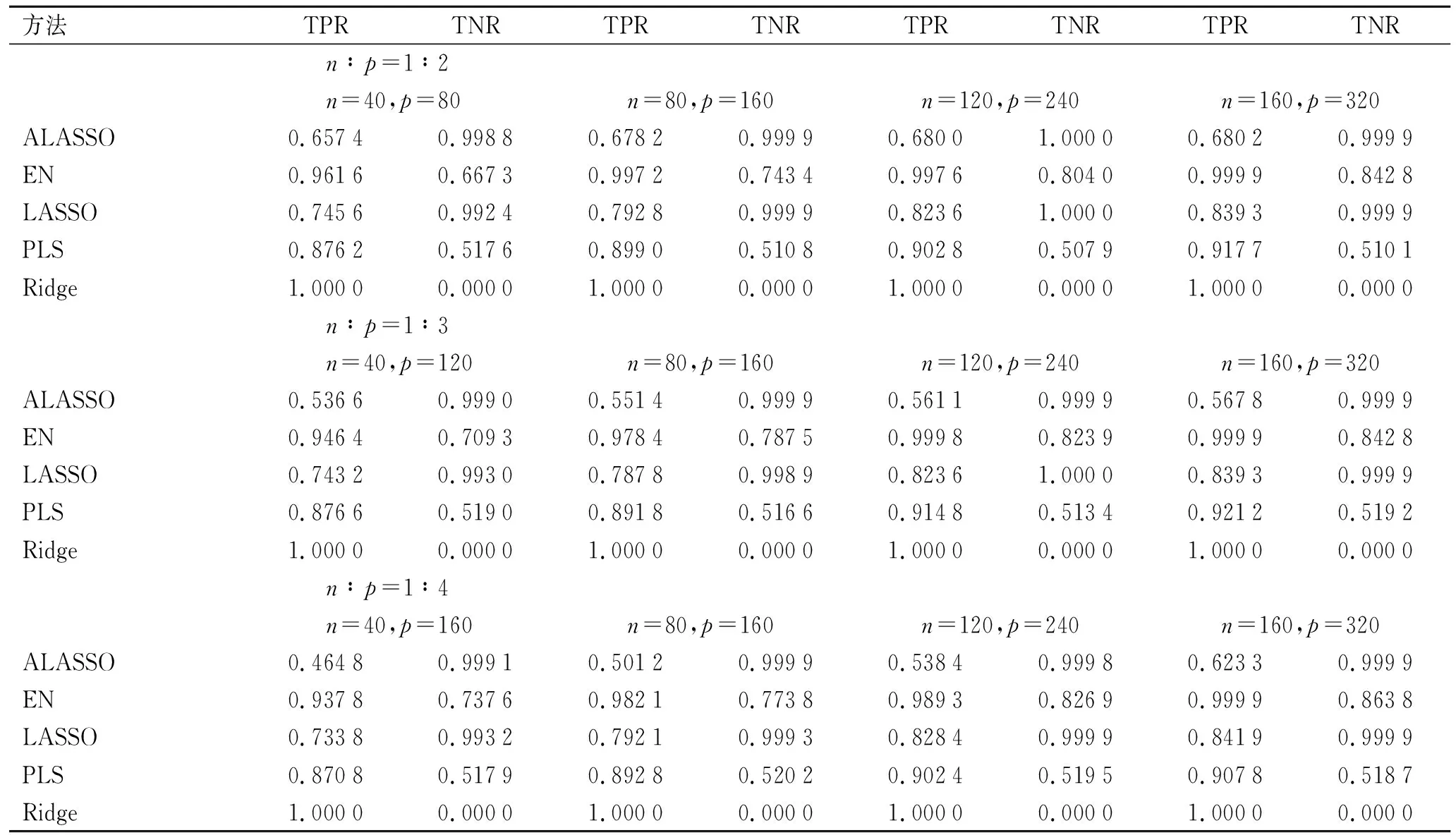
表1 自变量间线性独立条件下不同方法的变量筛选效果

2.2.2变量间线性相关条件下的筛选结果 第二部分模拟研中假设自变量间存在一定的相关性，即在变量间线性相关的条件下进行变量筛选，5种筛选方法的效果如下表2所示：

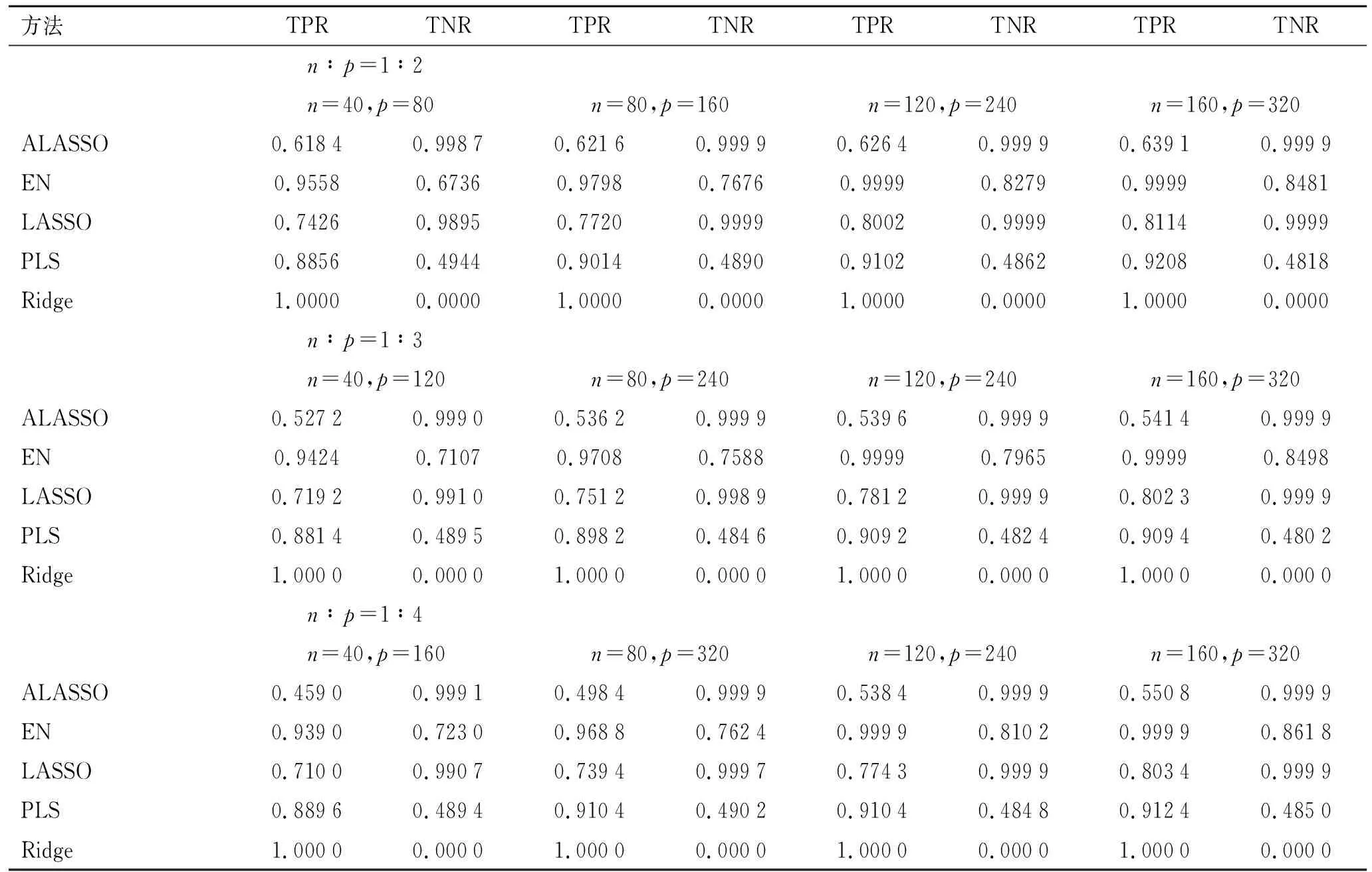
表2 自变量间线性相关条件下不同方法变量筛选效果

2.2.3样本量对变量筛选结果的影响 表1、表2的模拟结果显示，无论在自变量间是否存在关联性：

①在一定的n∶p水平下，随着样本量增大，EN方法的TPR、TNR均增大，变量筛选效果变好，过拟合、欠拟合的风险随之降低；但在一定的样本量下，随着样本量与变量数比例的增大(1∶1→1∶4)，EN方法的TPR略有减小，但TNR增大。

②在一定的n∶p水平下，随着样本量增大，PLS方法的TPR增大，TNR基本不变；在一定的样本量下，随着样本量与变量数比例的增大(1∶1→1∶4)，TPR减小，TNR亦基本不变。

③在一定的n∶p水平下，随着样本量增大，LASSO方法得到的TPR、TNR均增大，但TNR始终高于TPR；在一定的样本量下，随着样本量与变量数比例的增大(1∶1→1∶4)，TPR减小，TNR增大。

④在一定的n∶p水平下，随着样本量增大，ALASSO方法得到的TPR增大，但TPR水平总体仍较低，存在一定欠拟合的风险，TNR水平始终良好；在一定的样本量下，随着样本量与变量数比例的增大(1∶1→1∶4)，TPR有较大幅度减小，TNR基本保持一致且水平良好。

⑤Ridge算法无论在何种参数组合下，均没有起到变量筛选的作用。

2.2.4变量间相关性对变量筛选结果的影响 自变量间存在关联性时与自变量间独立时相比：

①EN方法的变量筛选效果较为稳健，且随着样本量增加效果越来越好。

②PLS方法的变量筛选效果也较为稳健，且随着样本量增加效果逐渐变好，但次于EN方法。

③LASSO和ALASSO方法的变量筛选效果受到变量间关联性影响较大，且ALASSO方法对变量间关联性更加敏感，两种方法相比，LASSO方法在变量间存在关联性时的变量筛选效果更好。

④无论在何种条件下，Ridge算法都没有起到变量筛选的作用。

3 讨 论

变量筛选在高维生物医学数据统计建模中扮演着十分重要的角色，它可以在保证模型稳定性的前提下减少候选变量的个数，更加充分和准确地挖掘变量之间的关系。实践中用于高维生物医学数据变量筛选的方法较多，但在方法的选择上并没有公认的标准和依据。本研究在简要介绍了5种高维数据变量筛选方法的基础上，通过Monte Carlo方法，设置适当的条件和参数，模拟分析对比了5种方法在高维数据变量筛选中的效果，为高维生物医学数据变量筛选策略的指定提供依据。

从模拟结果来看，样本量的增加对于变量筛选有较大影响。从模拟结果来看，无论何种方法，样本量越大，变量筛选效果越好。在高维生物医学数据的分析实践中，研究者往往对于变量数的多少更加重视，而容易忽略样本量的大小。尽管包括本研究所模拟的几种方法在内的许多变量筛选算法，都适用于变量数远大于样本量的情况，但如本研究结果所示，样本量的绝对大小依旧会影响变量筛选的效果。因此，即使在分析中使用了相关的高维数据变量筛选方法，也需要注意样本量的绝对大小，确保变量筛选的效果。

自变量间的相关性对变量筛选结果也有一定影响。模拟结果显示，在相关性存在的情况下，各种方法的变量筛选效果都会下降，但EN方法在样本量足够大的时候，依旧可以达到良好的效果，这与EN方法本身的特性有关。EN方法可以看作是LASSO和Ridge两种方法的结合，而Ridge方法是适用于变量间存在相关性的情况[7]。因此，EN方法兼有LASSO方法和Ridge方法的性质，对变量间的相关性容忍度很好。尽管很多分析模型都要求自变量间应尽量保持线性独立，但在高维生物医学数据的分析中，变量间存在相关性的情况几乎是不可避免的。因此，无论是建模分析还是在变量筛选，都应该对变量间的相关性予以充分的重视。

ALASSO方法在模拟中并没有在变量筛选中优于LASSO方法。相关研究认为，在较低维的情况下，尤其是当绝大部分自变量均与应变量相关时，ALASSO方法的效果可能会优于EN方法和LASSO方法[9]。本研究的模拟中仅有小部分自变量与应变量相关，这可能在一定程度上影响了ALASSO方法的变量筛选效果。

模拟研究也提示，Ridge方法对于自变量的筛选没有任何作用，因此不推荐在变量筛选过程中使用Ridge算法。Ridge算法虽然与LASSO方法都属于惩罚方法，但在进行系数压缩时，LASSO方法会将一部分关联性不显著的系数压缩至0，进而将这些变量筛选掉，而Ridge算法则仅将关联性较小的一部分变量的系数压缩至接近于0，因此无法起到真正的变量筛选作用。但根据相关研究的结果[10]，在完成变量筛选后的建模过程中，该方法依旧是有效的建模算法之一。

4 结论

模拟研究显示，在高维纵向数据的自变量筛选中，5种变量筛选方法在模拟研究中的变量筛选能力排序为EN>LASSO>ALASSO>PLS>Ridge。除Ridge算法外，其余4种方法在n∶p水平一定的条件下，增加样本量均可提高变量筛选的效果。变量间的关联性会对变量筛选结果产生影响，但EN方法(即弹性网算法)受其影响较小，最为稳健。因此，在高维生物医学数据分析的变量筛选中，更加推荐使用弹性网算法进行自变量筛选，但无论使用何种方法进行自变量筛选，充足的样本量都是自变量筛选获得良好效果的保证。