干热岩人工裂隙三维流动传热的数值模拟研究
2021-07-09冯雨晴汪道兵张凯鑫边雨辰
冯雨晴,汪道兵,秦 浩,张凯鑫,边雨辰
(北京石油化工学院机械工程学院,深水油气管线关键技术与装备北京市重点实验室,北京 102617)
地热能作为一种绿色清洁能源,不会排放二氧化碳、甲烷等温室气体而造成空气污染,符合当前的社会可持续发展战略。地热能还有一个特征就是其能量来源稳定,平均利用系数非常高,超过70%,目前国外己经建成的地热电站的利用系数高达95%,同时地热能电站也具有易于调节峰值、方便联网联供的优点。开采地热资源也比其他一般热源更为有利,主要原因在于夏天来临时,其可以自主进行能量回收,而这部分回收的能量又可以在冬天进行供热,这种循环方式既可以提高供暖水平,又可以降低能量损失[2]。所以高效开采地热资源将会为能源的发展带来质的飞跃。
地热资源主要分为浅层地热和深层地热,干热岩属于深层地热,是指温度150~650 ℃、埋深数千米、内部不存在流体或仅有少量地下流体的高温岩体[1]。开发干热岩可通过水力压裂造缝方式在地下形成一定规模的人工裂隙系统,然后向人工裂隙内注入工质进行充分热量交换,以提取地热能。裂隙渗流是地下流体渗流的主要形式,单一裂隙的水力特性的研究对理解干热岩的流动传热行为非常重要,国内外学者分别从干热岩裂隙换热实验和数值模拟方面进行了干热岩裂隙换热的相关研究。
在干热岩裂隙换热的实验研究方面,多个学者分析了不同因素对裂隙换热产生的影响。Auradou[2]主要针对单粗裂缝得出开度变化导致紊流的流动及对渗流变化产生的影响。任晔[3]研究认为,岩石裂隙填充物孔隙度、导热系数、岩石体积比热及其水平导热系数均属于低敏感性因素,而流体的流速、裂隙开度则均属于高敏感性因素。流体的相对温差随着岩石裂隙半开度以及流体流速的增大而增大。Zhao等[4]用人工劈裂的粗糙裂隙花岗岩进行换热实验研究,主要研究了流体流速和裂隙开度对换热的影响,结果显示增大流速和增大开度均提高了裂隙的换热能力。除了研究岩石自身性质变化对裂隙换热的影响,还有学者研究了改变外界因素对岩石换热产生的影响。赵坚[5]曾对花岗岩试样进行水力-热力实验,研究温度场对裂隙渗透性质的影响以及裂隙水与岩石基质之间的对流换热系数,得到对流换热系数与裂隙水的渗流速度有关的结论并与传热学理论中的经验公式相比较。Luo等[6]研究了不同围压(4~24 MPa)和温度(25~100 ℃)下单裂隙花岗岩的渗透性质,结果表明随着岩石温度的升高,裂隙水力开度呈减小趋势,水力传导系数却由于流体温度的升高而升高。Shu等[7]进行了25~200 ℃温度范围下升温、保温及降温过程对花岗岩水力特性的影响,结果表明,升温、保温及降温过程中裂隙开度及渗透率持续降低,升温过程中水力传导系数和换热效率升高,保温及降温过程中水力传导系数和换热效率持续降低。刘亚晨等[8-9]进行了70~290 ℃温度范围下单、正交裂隙花岗岩的渗透试验,研究了温度-应力-水力耦合作用下岩石裂隙结构面的渗透规律。结果表明高温高压下单裂隙岩样的渗透率随温度、围压的变化均符合指数函数关系,多条裂隙的渗透率可视为单条裂隙渗透率的线性叠加。Elias等[10]开展了不同岩性的岩石裂隙在不同温度、应力、化学条件下的渗流特性试验研究。程龙[11]开展了裂隙渗流传热机制研究,得出了在热扩散和热对流的共同作用下,裂隙中导热流体的温度分布随热传输过程的进行逐渐趋于平衡。热对流作用随着压力梯度的増大而増大。然而,通过实验难以获得人工裂隙不同位置内部的温度场和速度场的时空演化规律。
但是,由于干热岩所处地层应力高、位置深,难以获取实际岩石的内部结构和流体的温度变化,在对干热岩裂隙换热的研究方面,通常会采用数值模拟的方法,这种方法更为便捷、快速。在干热岩数值模拟方面,赵锟[12]以热交换和热传递的理论为基础,根据岩体和裂隙水的温度控制方程建立干热岩储层单条裂缝二维模型,通过ANSYS Fluent软件对沈阳地区干热岩温度分布情况进行了模拟计算。王如兵等[13]对单裂隙内渗流对温度分布影响机理的数学模型进行了探讨和分析,得到了单裂隙水流稳定温度场表达式,表明水流速度场的分布与温度场没有关系,温度场中的温度是渗流场中渗流流速的函数,渗流速度变化越大,温度场的分布变化也越大。Nemat-Nasser等[14]基于热储中的对流换热问题,推导出基于二维模型下的渗流传热过程的基本方程。Ogino等[15]用数值方法模拟了流体与高温裂隙岩体之间的对流换热过程,并考虑了局部对流换热系数的差异。高雪峰等[16]以花岗岩材料参数为基础,建立具有单一裂隙单元的二维数值模型,在不同的初始温度和流速下进行数值模拟,研究了单一裂隙通道表面几何形态对换热特征的影响规律。Pruess[17]研究了一定范围内传热的瞬态平衡问题,得出基岩与裂隙之间渗流传热问题的解析解。朱家玲等[18]应用局部非热平衡法,依据岩体截面二维导热方程推导出单裂隙流固换热系数解析解,并对解析解进行敏感性分析。张树光等[19]建立了裂隙岩体的几何模型,并对岩体与裂隙水流之间发生的对流换热现象进行分析,模拟得出在渗流作用下岩体内的温度场分布规律。Jiang 等[20]开展了裂隙渗流传热的数值模拟和实验研究,结果表明,对于充分发展的渗流传热区域,岩石裂隙的局部传热效率随着流速的增长不发生明显变化。张正[21]利用ANSYS Fluent模拟软件进行数值模拟计算,在某一固定流速下,干热岩系统出水温度在某一时间段内都会有显著地提升,并逐渐趋于稳定,最后恒定为固定温度。
上述数值模拟主要以二维模型为主,实际上干热岩裂隙换热过程为三维模型,二维模型的数值模拟对于干热岩裂隙换热的研究不够全面,因此,笔者建立了干热岩单裂隙的三维模型,具体考察了单因素裂隙内流体温度的变化规律,分别从流入速度、裂隙长度、裂隙宽度等因素进行模拟试验,研究裂隙传热过程的一般规律,分析了以上因素对换热强度的影响。
1 物理模型
干热岩裂隙流动传热模型如图1所示,为了保证模拟计算的精度和效率,对其进行了网格划分,结果如图2所示。在网格划分时,设置划分数为30个单元,单元尺寸为10 mm,并对裂隙内流体流经的部分进行加密,采用四面体网格,远离人工裂隙的岩石基质部分采用较粗的八面体网格,以避免计算耗时过长。
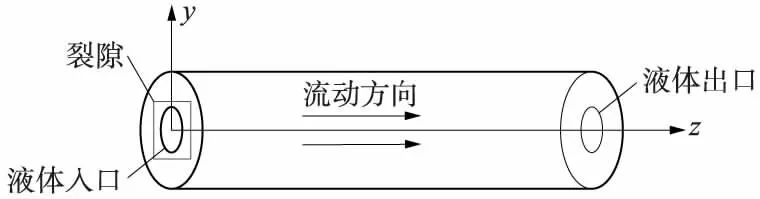
图1 流动热传导示意图

图2 模型网格划分示意图
将人工裂隙假设为细长的三维圆柱管束,具体假设条件如下:
(1)人工裂隙周围岩体均为花岗岩,将花岗岩设置为固体域;流体在人工裂隙内流动换热,将人工裂隙设为流动域;
(2)与人工裂隙流动能力相比,周围的岩石层的渗透性能较低,因此流体仅在裂隙内部沿裂隙方向流动;
(3)为方便网格划分,将人工裂隙和岩石基质简化为三维圆柱体。
2 数学模型
在模拟计算中做出如下假设:流体为不可压缩水,模型为三维模型、非稳态,在计算区域始终处于湍流状态,忽略黏性耗散,不考虑重力作用。
2.1 不可压缩流体与流动换热的控制方程
不可压缩流体与流动换热的控制方程为:
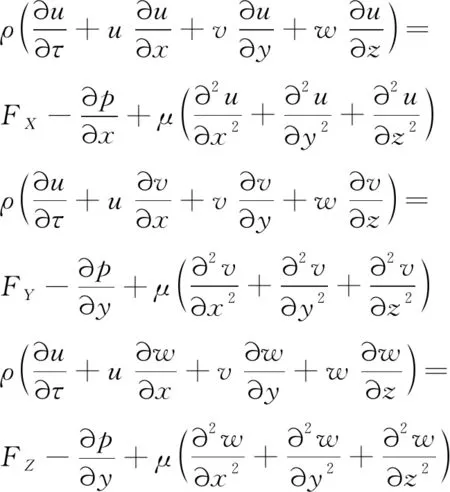
(1)
式中:ρ为流体密度;p为压力;u、v、w分别为流体在t时刻沿x、y、z方向的速度分量;FX、FY、FZ分别为单位体积流体在x、y、z方向上受的外力;μ是注入工质的动力黏度。
2.2 连续性方程
连续性方程为:
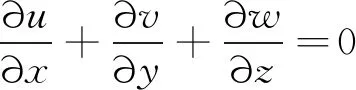
(2)
2.3 能量守恒方程
能量守恒方程为:
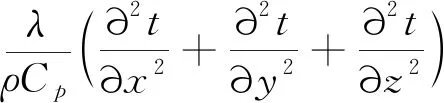
(3)
式中:λ为干热岩导热系数;CP为干热岩比热容;t为温度;τ为时间。
3 数值模拟
3.1 边界条件及物性参数
计算区域的边界条件设定如下:
3.1.1 入口处
流体入口采用速度入口边界条件,假定流体不可压缩,并且流体速度已知,因此入口流速取值分别设置为0.1、0.2、0.3 m/s。
3.1.2 出口处
流体出口采用压力出口边界条件,为模拟干热岩地层的压力,将出口压力取值为40 MPa。
3.1.3 岩石壁面
圆管壁面均采用壁面边界条件。
在模拟计算中流体为水,管壁材质为干热岩,其物性参数如表1所示。

表1 基础物性参数表
3.2 模拟方案
假定干热岩水力压裂产生的人工裂隙处于深度为3 500 m的岩层中,干热岩温度恒定为473 K,由于流体的流出温度受入口速度、裂隙宽度、裂隙长度、流体初始温度等因素的影响,所以分别对这些因素影响下的流体流出温度变化进行模拟求解,并对数值模拟结果进行对比分析。
该模型的换热过程发生在岩石层内部,换热形式为流体在裂隙内与周围岩石进行热量交换,所以将模型设置为裂隙内部水-岩换热的形式。
在计算过程中,先对裂隙进行分析,建立描述注入流体(水)在单裂隙内流动的裂隙模型,注入的流体仅在裂隙内流动。岩体可以简化为均质各向同性的连续介质模型,忽略岩块的渗透性。假定岩体存在单一裂隙,裂隙长度远远大于裂隙宽度。
模型参数设置如表2所示。
3.3 模拟结果及分析3.3.1 出口面温度分析
不同裂隙宽度、裂隙长度、流入速度条件下,流过裂隙的流体温度变化曲线如图3所示。
(1)不同裂隙宽度
由图3可知,流体在流经不同宽度的裂隙时,温度受到的影响也不一样。在岩石裂隙长度与流入速度一致时,裂隙宽度越小,出口处流出的流体的温度越高,随着时间的增加,温度逐渐趋于平缓。由图3(c)中可以看出,在裂隙长度为3 m、流入速度为0.3 m/s的条件下,裂隙宽度为10 mm时,出口处流体温度为397 K;裂隙宽度为8 mm时,出口处流体温度为406 K;裂隙宽度为6 mm时,出口处流体温度为420 K,可以看出,同一模型在不同裂隙宽度时,温度相差十分明显。由图3(e)中可以看出在不同裂隙宽度下每组模型中流体流经出口时达到的最高温度。由此可知,在裂隙长度、流入速度相同时,出口处流体的温度随裂隙宽度增加而下降。
(2)不同裂隙长度
由图3(c)可知,当裂隙宽度、流入速度相同时,随着裂隙长度的增长,沿着裂隙流出的流体温度也会升高,裂隙长度为1 m的模型流体温度为392 K;裂隙长度为3 m的模型流体温度为420 K,2组模型之间温度相差为28 K。由图3(d) 可以看出,不同裂隙长度下,出口处流体温度随裂隙长度的增大上升趋势明显。所以流体所流经的裂隙长度越长,流出时的流体在受到更长时间的热传递的影响下,温度增大程度越大。
(3)不同流入速度
由图3中可以看出,流体流入的初始温度都是373 K,随着时间增加,温度在升高到一定幅度后慢慢趋于稳定。由图3(a)中可以看出,流入速度为0.1 m/s时,出口处流体的温度最高的一组为457 K;由图3(b)中可以看出,流入速度为0.2 m/s时,出口处流体的温度最高的一组为433 K;由图3(c)中可以看出,流入速度为0.3 m/s时,出口处流体的温度最高的一组为419 K。由此可知,流入岩石裂隙速度越慢的流体,在流出时流体的温度就越高。图3(f)为流体流出出口时所能达到的最高温度,当岩石裂隙宽度、长度相同时,流速越小,流体出口处温度越高,与周围岩石进行热交换的时间越长,使得换热过程更加充分。
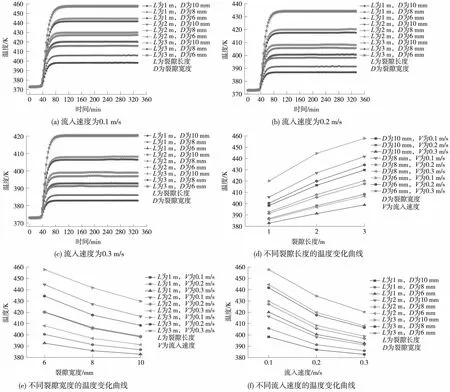
图3 不同条件下的温度变化曲线
3.3.2 出口面温度云图
岩石的横切面在160 s时不同裂隙宽度的温度云图如图4所示。
从图4中可以看出,裂隙宽度对出口处流体的影响很大,岩石外壁初始温度为473 K,内部流体区域的初始温度为373 K,本组模型的升温幅度范围在27~82 K左右。通过岩石横截面观察到,温度由岩石外壁向内部传递,将热量传递到流体区域,裂隙宽度越小,横截面中流体所圈出来的流体的区域温度越高。将图4(i)与图4(c)进行对比发现,裂隙宽度为6 mm的模型岩石裂隙中的流体温度为445 K,要高于裂隙宽度为10 mm时温度为410 K的流体。所以相同裂隙长度和流入速度的情况下,裂隙宽度越小,沿裂隙流出的流体温度越高。

图4 同一时刻不同裂隙宽度的温度变化云图
由图5中可以看出,裂隙长度对于流经流体的温度影响显著。流体沿z轴正方向流动,流体从进口处流入到出口处流出过程中,在入口处温度颜色较深,温度较低,与初始设置的373 K相差不大;流体沿着裂隙流动,温度逐渐上升,云图中流体区域的颜色也逐渐变浅。裂隙长度为1 m时出口处流体温度为396 K;裂隙长度为2 m时出口处流体温度为415 K;裂隙长度为3 m出口处流体温度为430 K。所以,裂隙的长度越长,流体在裂隙中升高温度的幅度就越大,出口处流体的温度也就越高。

图5 同一时刻不同裂隙长度的温度变化云图
4 结论
通过建立干热岩单裂隙流动换热的三维数值模型,以干热岩热力学参数为基础,利用ANSYS Fluent商业软件进行了相关数值模拟计算,研究了人工裂隙宽度、流体流入速度及裂隙长度对干热岩裂隙内流体温度的影响,主要结论如下:
(1)在岩石裂隙长度与流入速度一致时,裂隙宽度越小,出口处流出的流体的温度越高;裂隙长度增长,也使流出的流体温度升高,流体所流经的裂隙长度越长,流出时的流体在受到更长时间的热传递的影响下,温度增大程度越大;
(2)流体流入的初始温度都是373 K,随着时间增加,温度在升高到一定幅度后慢慢趋于稳定。岩石裂隙宽度、长度相同,流速越小,流体出口处温度越高,流入速度越慢,换热时间就更长,传递的热量就越多。
(3)为了利用干热岩热能,提供足量的高温度液体,裂缝宽度决定了出口的温度。裂缝宽度越大,能够使得足够多的流体升温到与基岩一样的温度。在可能的情况下,应增加裂缝的宽度,以提高注入量或提高流体升温幅度。
(4)对于不同的裂缝宽度及不同的流入速度,裂缝长度(升温距离)达到一定程度后,水温才能升高到与基岩一致。可见在可能的情况下,必须提高裂缝的长度;裂缝宽度越小,在给定的流入速度下,达到最高温度所需要的裂缝长度越长。当裂缝宽度不足时,可以通过增加裂缝长度达到使高排量流体升温的目的。
