基于遗传算法的平面移动式立体车库存取调度优化
2021-07-09杨佳衡沈伟东钟浩翔朱亚东邓黎明
陈 亚,杨佳衡,沈伟东,钟浩翔,朱亚东,邓黎明
(1.北京石油化工学院机械工程学院,北京 102617; 2.中国联合网络通信有限公司勃利县分公司, 黑龙江 勃利 154500;3.北京化工大学机电工程学院,北京 100029)
随着我国汽车保有量的急剧增加,“停车难”问题日益突出,而立体车库是解决停车难的有效途径[1-2]。立体车库调度策略是影响立体车库工作效率的关键,因此研究立体车库调度策略对提升车库服务能力、客户满意度及车库的竞争力具有重要的现实意义[3]。
常见的车库存取调度优化算法有遗传算法、蚁群算法、粒子群算法等,很多学者基于以上算法对立体车库调度问题进行了深入研究。Manzini R等[4]提出了适用于智能仓储系统的多参数动态优化模型,对立体车库的分区存储具有一定的参考意义。Potrco I等[5]对巷道堆垛式立体车库建立了时间模型,基于时间模型优化了车辆出入库顺序。日本学者Motoji等[6]研究了巷道堆垛式立体车库服务时间与入库位置的正相关性,给出了多任务状态下库位的最短路径。Tone L等[7]在多巷道立体车库的库位存取任务方面提出了一种启发式服务规则。Chen等[8]使用遗传算法确定好存取目标车位后,利用Petri网进行路径规划,以节省存取时间。李剑锋等[9]采用改进遗传算法对巷道堆垛式立体车库存取车时间进行建模优化,得到最优的存取车耗时。孙军艳等[10]利用改进的交叉算子遗传算法,分别对3种不同库容的升降横移式与巷道堆垛式立体车库进行存取车调度优化。周雪松等[11]采用融合遗传算法和蚁群算法的GAAA算法来搜索立体车库存取车的最短路径。李建国等[12]以排队论为基础,使用分区调度的策略进行编程仿真,为立体车库选择合理的调度策略提供了量化分析的依据和理论参考。陈桂兰等[13]提出一种改进混合粒子群算法,应用于立体车库存取策略时间模型,寻找存取车最优时间和最优排序。
对存取车任务进行车位分配的实质是规划升降机与泊车机器人的运动路径,使存取车总时长最小,因此可以将立体车库车位分配问题看作旅行商(Traveling Salesman Problem, TSP)问题进行研究。旅行商问题的研究广泛应用于车间调度、网络路由、车辆路径、航迹规划等领域。笔者通过分析存取车详细的流程,建立车库存取时间模型,利用遗传算法对车位分配进行优化,通过仿真及实验得出算法对时间的优化结果。
1 车库调度模型的建立
1.1 平面移动式立体车库结构
平面移动式立体车库是采用智能泊车机器人与升降机配合,将载车板与汽车搬运至指定车位或者搬运至进出口实现车辆存取的机械式停车设备。该类车库的特点为,升降机实现车辆垂直方向的运动,泊车机器人实现车辆水平方向的运动。车库中采用的泊车机器人为全向移动式泊车机器人,因此存取车更为灵活,效率更为高效。
平面移动式立体车库结构如图1所示,车库为M层N排K列,第 1 排的 1 列与 2 列为升降机所在位置,2 排至N-1 排的第 1 列位置为泊车机器人通过的巷道,每排车位之间也是巷道,因此,车库共设有M×N×(K-1)个车位。车库的出入口设置在 1 层 1 排升降机所在位置。
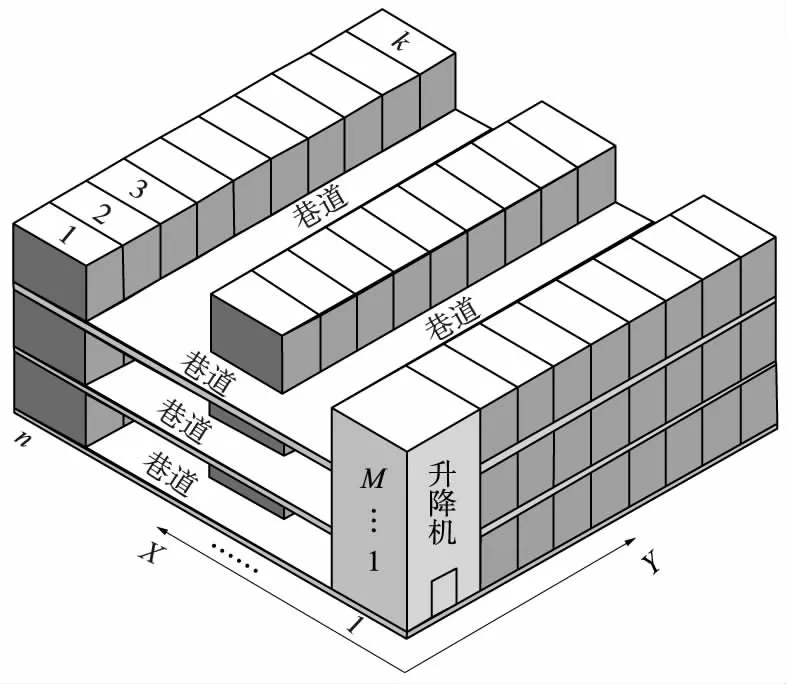
图1 平面移动式立体车库结构示意图
1.2 TSP问题描述
TSP问题是已知n个城市两两之间的路径,商人从某个城市出发遍历所有的城市且每个城市只能拜访1次,求其安排的旅行顺序使商人总路径最短。用图论对其描述即为:假设有1个无向图G=(V,W),其中V={V1,V2,…,Vn}是节点集,W={WViVj},(Vi,Vj∈V)是节点Vi与Vj之间对应的代价所组成的代价矩阵。所以TSP问题即为求1个排序:
O={O1,O2,…,On},On∈V(i=1,2,…,n)使式(1)最小,其中On+1=O1。
(1)
在立体车库中,起点车位与终止点车位均为车厅位置车位,车位与车位之间执行任务的时间为对应节点的代价,对于立体车库存车任务分配的车位也只能分配该车位1次,单次取车任务车位固定,在本次存取任务序列中也只能分配1次,因此可以将立体车库车位分配问题看成典型的TSP问题进行研究。
1.3 车库存取车调度策略
平面移动式立体车库运行过程中,存取车是由泊车机器人与升降机配合完成。根据平面移动式立体车库的存取车运行过程,车位的分配直接决定了存取车时升降机与泊车机器人行驶距离的长短,升降机与泊车机器人的待命位置也同时影响了存取车时泊车机器人与升降机的运动路径,从而影响完成任务的时间。因此,升降机、泊车机器人的待命位置选择与车位的分配是立体车库存取车优化的关键。
常见的立体车库存取调度策略有4种,如表1所示。

表1 调度策略分类
综上所述,存车优先和取车优先分别适合存车高峰期与取车高峰期,存取车效率比较高,但是泊车机器人与升降机空载路程较长,而交叉存取与原地待命策略能有效避免泊车机器人与升降机产生多余的空载动作,从而达到节能的目的。而交叉存取本质上是以原地待命为基础对存取车任务进行两两分组,前后搭配进行存取,当存取车任务量相差较大,分组将会陷入被动。因此,选择原地待命调度策略进行建模。
1.4 原地待命策略的时间模型
为了建立一个合适的符合实际的数学模型,进行了如下假设:
(1)车库初始为空,升降机和泊车机器人初始位于车库车厅出入口位置;
(2)存取车的车辆都能通过车辆安全检测,顺利出入库;
(3)提升系统电机抱闸减速距离忽略不计;
(4)忽略泊车机器人加速时间和减速时间;
(5)泊车机器人和升降机无论是否负载,速度一致;
根据车库实际实验情况所建立的模型参数设置如表2所示。

表2 立体车库参数设置
根据任务分配的优化原则,选择存取车时间最短作为调度优化的的目标,建立存取车总时间数学模型。
存取车总时间的计算式为:
T=Te+Tr
(2)
其中:Te为升降机运行时间;Tr为泊车机器人运行时间。升降机运行过程分加速、匀速、减速的过程,则升降机将车辆和泊车机器人从i层运至第m层或从m层运至i层所需时间为:
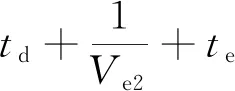
(3)
但当m=1且i=1时t1↔1=te。
泊车机器人在某车位[ni,kj]和指定车位[n,k]之间运动所需时间为:
t[ni,kj]↔[n,k]=
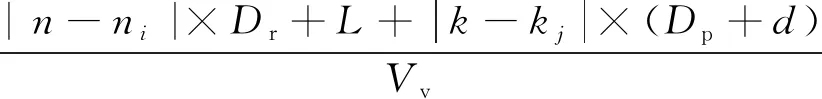
(4)
其中,升降机可以看成是车位[1,1],但当ni=n时

(5)
根据上次任务原地待命的位置和此次存取车任务的不同,可分为4种情况进行讨论:
(1)当上次任务为取车任务,则泊车机器人与升降机都在车厅位置待命,此次为存车入库任务,任务执行总时间为:
T=t1↔m+t[1,1]↔[n,k]
(2)当上次任务为取车任务,此次也为取车任务时,同理可得:
T=2t1↔m+t[1,1]↔[nz,kz]+t[nz,kz]↔[n,k]+t[1,1]↔[n,k]
其中:nz、kz分别为放置载车板的目标空车位所在排和列。
(3)当上次任务为存车任务,此次为取车任务时,取车车位与待命车位分为同层与不同层2种情况:
①当取车车位与待命车位同层时,取车出库任务执行总时间为:
T=t1↔m+t[nd,kd]↔[n,k]+t[1,1]↔[n,k]
其中:nd、kd分别为待命车位所在排和列。
②当取车车位与待命车位不同层时,取车出库工作总时间为:
T=tmd↔m+t[1,1]↔[nd,kd]+2t[1,1]↔[n,k]
其中:md、nd、kd分别为待命车位所在层、排和列。
(4)当上次为存车任务,此次仍为存车任务,存车车位与待命车位分为同层与不同层2种情况:
①当存车车位与待命车位同层时,存车入库任务执行总时间为:
T=2t1↔m+t[nd,kd]↔[n,k]+2t[1,1]↔[n,k]
②当存车车位与待命车位不同层时,存车入库工作总时间为:
T=tmd↔m+2t1↔m+t[1,1]↔[nd,kd]+3t[1,1]↔[n,k]
因此,总存取车时间最短的目标函数为:

(6)
其中:Ti为第i次存取车任务所用时间;R为存取车任务总数。
2 基于遗传算法车位分配优化
2.1 遗传算法优化策略
遗传算法是一种基于概率的搜索最优值算法,是模拟生物染色体遗传变异进化过程进行迭代,其具有较强的全局搜索能力与自适应性。使用遗传算法进行寻优计算的主要优势在于,遗传算法使用大量并行计算提高计算速度,并且寻优过程并非随机试探,而是通过概率实现,本身具有良好的灵活性,通过交叉变异操作产生优良个体,因此十分适合求解大规模的复杂优化问题。
2.2 车位分配的遗传算法实现
遗传算法实现涉及的主要因素包括参数的编码、初始群体的设定、适应度函数的设计、遗传操作、算法控制参数的设定和约束条件的处理。
(1)在立体车库车位分配问题中选取整数编码方式,首先对车库中车位进行绝对车位的编号;然后对存取车的汽车数目进行编号;最后在车库中随机选取任务数目数值,即为存取车车位号。一条染色体编码方式即为车位分配的可行解之一,染色体的长度为存取车任务数目,基因就是空车位,基因与染色体位置上的车辆编号对应。如车库中有7辆车需要进行存取,存取车车位按照从小到大排列为1~7染色体的基因随机产生,具体的存取任务与存取车位编号如表3所示。

表3 存取车任务示例表
由表3可知,1号存车车辆分配到9号车位,2号取车车位在2号车位,即(9|2|13|5|8|11|17)为一条染色体,也即为一种车位分配方案。
(2)选择的策略为原地等待策略,选取存取车总时间最短为目标,都是以最小值为目标的优化,函数值越小的个体适应度值越大,因此,将函数值的倒数作为适应度值。
存取车时间最短的适应度函数为:
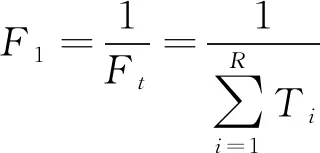
(7)
(3)采用最优保存的选择策略,其适应度最高的个体直接替换子代交叉变异后适应度最差的个体,因此可以确保其种群优良性;使用单点交叉方式随机在父代基因生成一个交叉点;在随机生成的变异的基因位置,互换其两侧的基因,生成新的子代个体。
3 仿真与实验分析
以3层7列平面移动式立体车库为研究对象,其车位分布如图2所示。
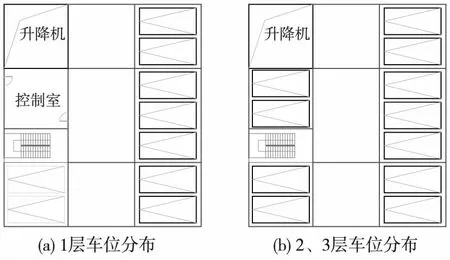
图2 立体车库车位分布
存车车辆可以放入路径最短空车位中,取车车位固定。鉴于忙期分为存车高峰期与取车高峰期以及存取车任务量相等的情况,因此需要对不同情况进行仿真分析,进而求得最佳车位分配策略。经过试验选择遗传算法控制参数,如表4所示。

表4 遗传算法参数
3.1 存车任务数大于取车任务数的情况
以存车任务为10,取车任务为4为例,具体存取车车位如表5所示。
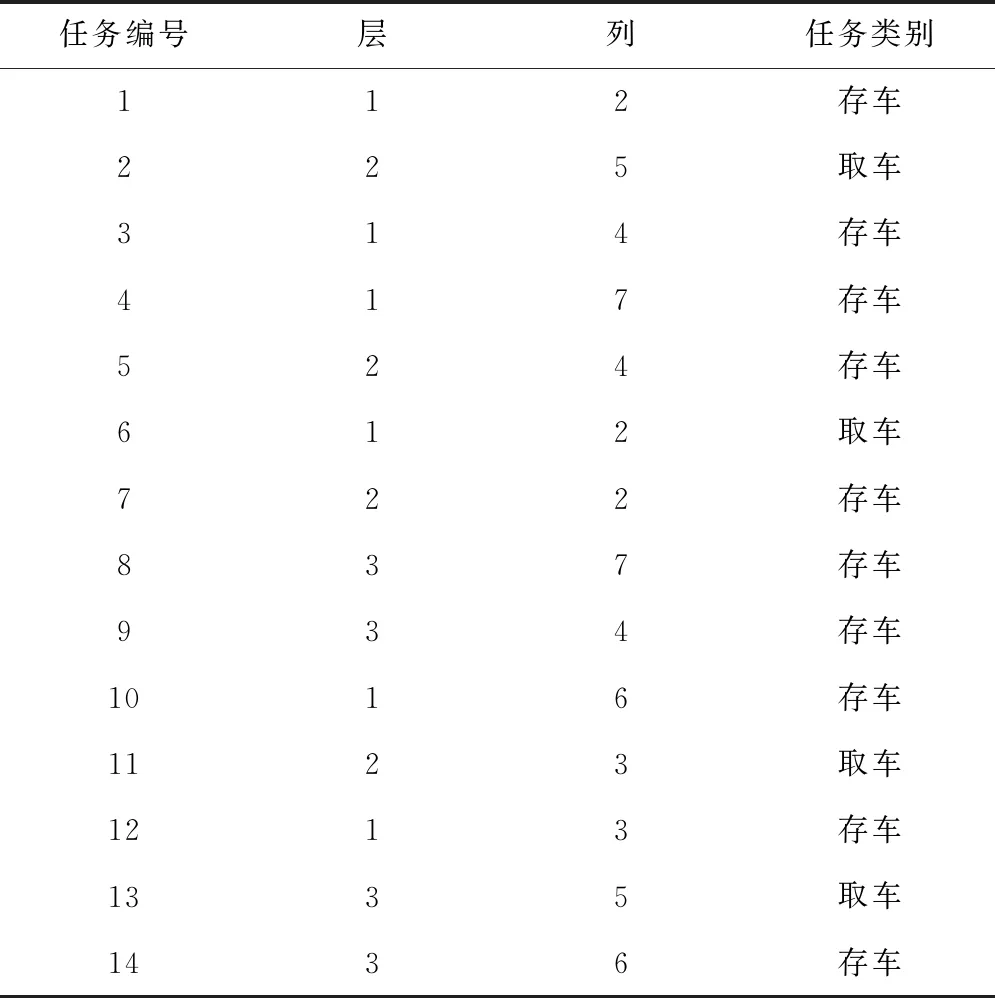
表5 存车高峰时存取任务
使用遗传算法对原地待命策略进行优化仿真,重复运行10次,以平均值计数,结果如表6所示。

表6 存车高峰仿真优化结果
使用遗传算法对时间进行优化后所得的存取顺序为(11|12|2|3|1|6|4|10|7|5|13|14|9|8|1),仿真所得存取顺序如图3所示,图中横坐标为楼层,纵坐标为车位所在列。

图3 存车高峰时优化后的存取顺序图
3.2 取车任务数大于存车任务数的情况
以取车任务为10辆,存车任务为4辆为例,存取车车位如表7所示。
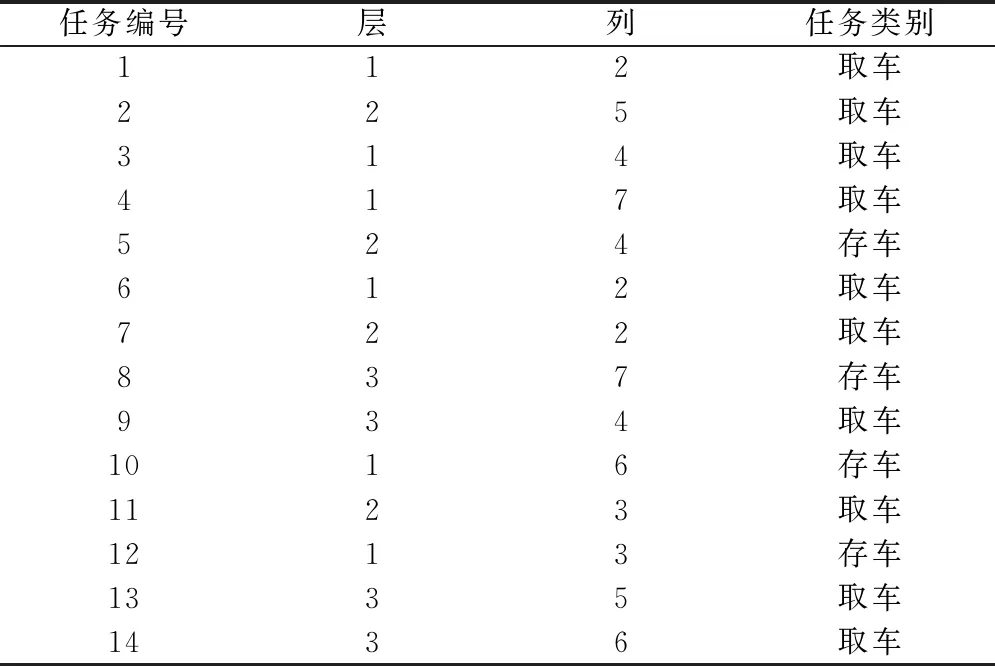
表7 取车高峰时存取任务
优化后所用时间如表8所示。仿真所得存取顺序如图4所示。

表8 取车高峰仿真优化结果
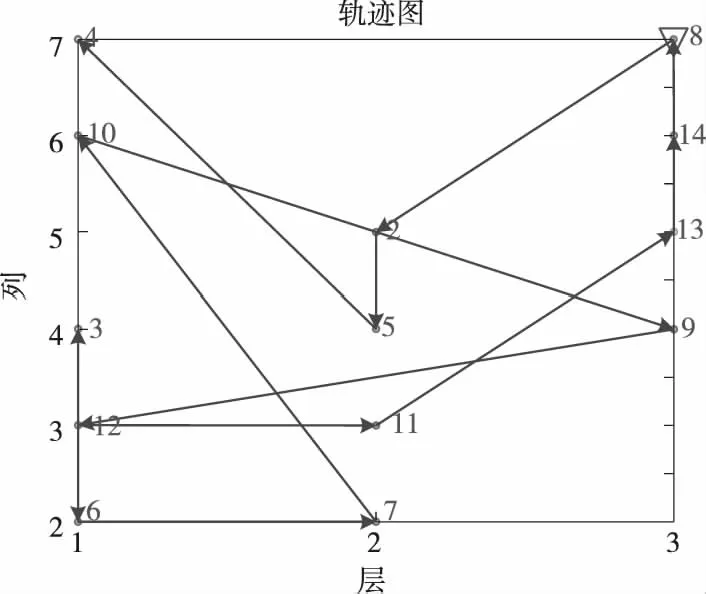
图4 存车高峰时优化后的存取顺序图
3.3 当存车取车任务量相近或相等的情况
以取车任务为7辆,存车任务为7辆为例,存取车车位如表9所示。

表9 存取任务量相等时存取任务
优化后所用时间如表10所示。仿真所得存取顺序如图5所示。

表10 存取任务相近情况仿真优化结果
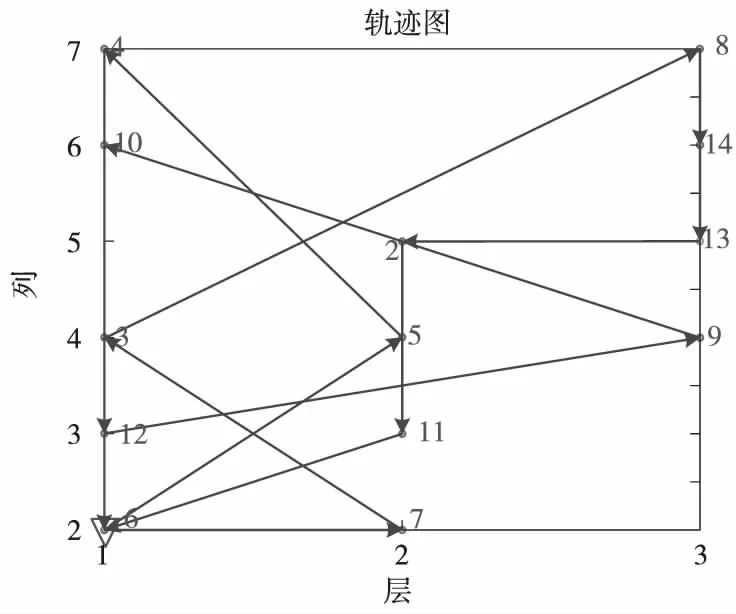
图5 存取车任务量相等时优化后的存取顺序图
对比随机存取与优化前后的时间,所得结果如表11所示。
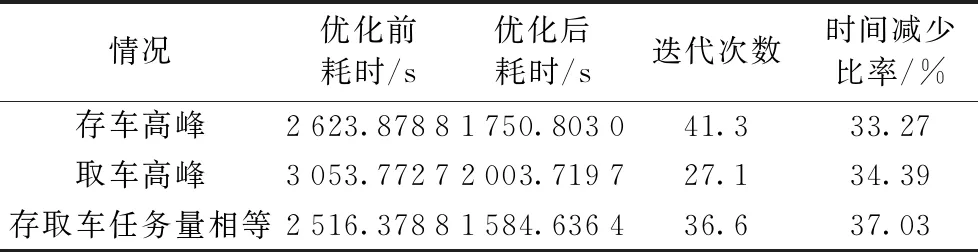
表11 时间优化结果对比
通过优化前后的时间对比,可以得出存取车总时间相比优化前缩短了33%以上,最高为存取任务数相等时,达37.03%。
在仿真实验的基础上,对实际立体车库(见图6)进行了测试,随机产生了5个车位的存取车任务,如表12所示。

图6 平面移动式立体车库实景图
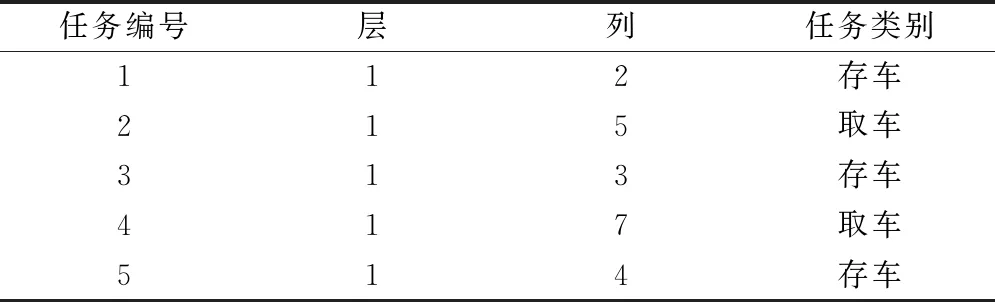
表12 存取车试验任务
根据原地等待策略,分别按照随机分配车位的存取与经过遗传算法优化后的存取顺序执行存取任务,对比完成 5 次存取任务的总时间,结果如表13所示。

表13 实验存取总耗时对比
实验结果表明,仅对5次存取任务进行优化总耗时就可以节省166.44 s,效率提高15.68%。实验结果验证了该遗传算法能有效提升车库存取效率。
4 结论
(1)根据平面移动式立体车库调度过程中车位分配特点,将TSP应用问题推广到平面移动式立体车库存取车任务调度优化中,在已有的立体车库结构与性能参数基础上,选择原地待命策略对立体车库存取车时间进行数学建模。
(2)使用遗传算法对存取车车位分配进行优化,实验结果表明,该遗传算法减少了平面移动式立体车库执行任务的总耗时,存取效率有了明显的提高。
(3)验证了运用遗传算法的平面移动式立体车库调度系统对提升车库运行效率的有效性与可行性,从而为提高车库运营效益与客户满意度方面提供参考依据。
