基于内模控制器的直流伺服电机速度控制方法

徐 勇，张智华，龚 旭，李胜永

（1.江苏航运职业技术学院交通工程学院，江苏南通226010；2.上海理工大学光电信息与计算机工程学院，上海200093）

随着工业自动化程度的不断提高，促使了直流伺服电机被应用到了越来越多的工业场合［1］。直流伺服电机是一个具有稳定特性的标准二阶系统，具有很高的工业适用性［2-3］。近年来在机械臂、机床以及轧机等应用中都用到了直流伺服电机。直流伺服电机的广泛应用，促使了人们对其速度控制的要求也越来越高［4-5］。

通过学者们的研究，出现了较多直流伺服电机的控制方法。文献［6］中为了解决了电机参数变化和负载转矩扰动的问题，提出了一种基于扩展状态观测器的直流伺服电机控制方法，利用扩展状态观测器方法，在外界干扰部分未知的情况下准确地估计无刷直流电动机的转矩，并利用动态表面控制技术设计控制器，以控制电机速度。Kumar等［7］采用带电容的六开关逆变器，将单相逆变器逆变为几段式逆变器后，再利用无刷电机功率与速度传感器直接调速。文献［8］在有效目标函数积分时间绝对误差（ITAE）的基础上，利用PSO、Bat和Firefly算法等生物激励优化技术对PID控制器参数进行在线整定，采用PID控制器实现永磁同步电机的速度控制。这些方法都能对直流伺服电机的速度进行控制，但控制结果的准确度和平稳性都不高。

对此，本文通过对直流伺服电机的模型进行分析，获取其传递函数。引入分数阶积分器，在其传递函数的基础上，计算CRONE控制方法的开环和闭环传递函数，利用CRONE控制方法的闭环传递函数构造内模控制器，并以内模控制器为中心，建立了内模控制系统，以求取系统的输出速度。通过利用本文方法和干扰观测器PID方法，对阶跃变化和曲线变化的参考速度进行跟踪，以验证本文方法跟踪性能的有效性与优越性。

1 直流伺服电机模型分析

由电枢绕组电阻和电枢绕组电感组成的电枢控制直流伺服电机结构示意图如图1所示［9］。图中：ia为电枢绕组电流，ω为转子角速度，R为电枢绕组电阻，L为电枢绕组电感，Kb为反电动势常数，u为电枢绕组输入电压，J为系统惯性矩，d为系统阻尼系数，M为负载的质量。

图1所示直流伺服电机工作时，在输入电压为u的状态下，电路平衡的计算过程为［10］

图1 电枢控制直流伺服电机结构示意图Fig.1 Structure diagram of armature control DC ser vo motor

式中：Ce为电机感应电动势系数；β为磁通量。

直流伺服电机力矩的计算过程为

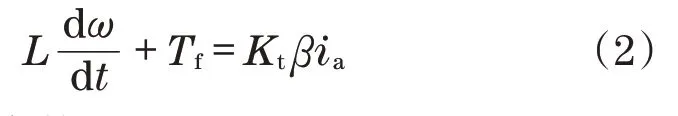
式中：Kt为转矩常数；Tf为阻力力矩。

电枢控制直流伺服电机的线性化机电动力学可以描述为

直流伺服电机可以用线性时不变单输入单输出（SISO）系统来表示，其对应的传递函数为

式中：η为转换增益。

在获取传递函数后，需要设计一个如图2所示的反馈配置中的控制器C（s），使得直流电机能够稳定准确地跟踪参考速度。图中：ωf为输入的参考速度，D为外部干扰。

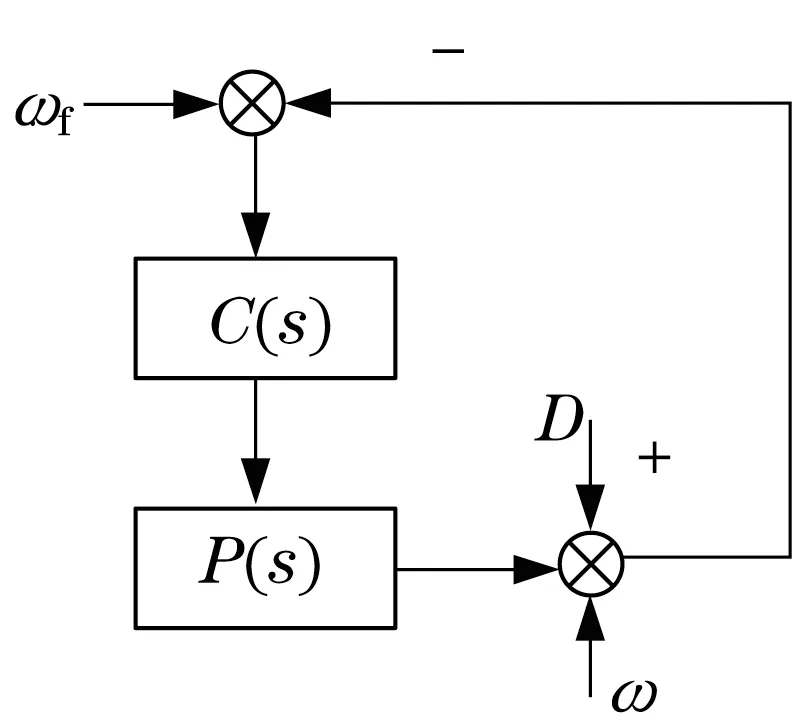
图2 反馈配置示意图Fig.2 Feedback configuration diagram

2 内模控制器设计

分数阶微积分是对非整数阶算子积分和求导的推广。近年来，在控制系统设计中，基于分数阶的控制策略已成为一个活跃的研究领域。在分数阶系统中，控制系统动力学的方程可以是任意阶的。分数阶系统由分数阶积分器和微分器两部分组成，分数阶积分器的传递函数可定义为［11］

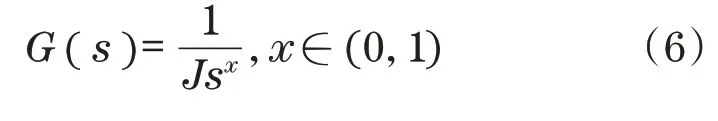
当x=1时，G（s）为一个简单的纯积分器。当x减小到0时，由于s0=1，传递函数的积分作用就被消除了。纯积分器的加入会减慢响应速度。从式（6）可见，分数阶积分器能够避免纯积分器的出现，保证了系统的响应速度，为系统速度的准确控制提供了时间上的支持。

式（6）的谱传递函数以及相位可分别表述为

式中：ai≠0，且y m>y m-1>…>y1。

Dv≡0Dvt是关于变量t的v阶Caputo分数导数，在起始时间t=0时分数阶导数的表达式为

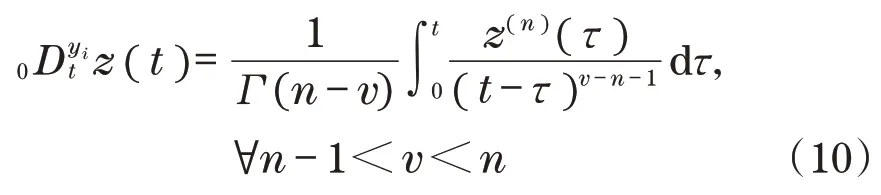
式中：z（n）（t）为z（t）相对于t的n阶导数；Γ(·)为伽马函数。

CRONE控制方法是一种频域方法［12］。在CRONE原理中，开环传递函数由分数阶积分器定义。通过分数阶积分器G（s）定义的关于图2所示反馈配置的CRONE开环传递函数为［13］

阶数α、增益交叉频率Ωgc分别确定输出响应的超调量和速度。T（s）的相位裕度计算过程为

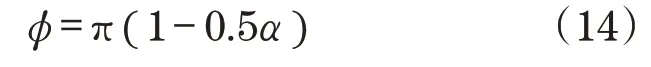
由式（14）可见，T（s）的相位裕度与系统增益k无关。

T（s）的谱传递函数为［14］

在T（s）的基础上构造的内模控制器为

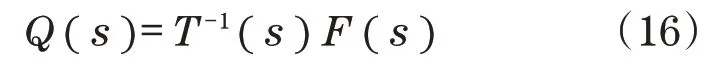
式中：F（s）为分数阶形式的内模控制滤波器，其表述为

式中：λ为保持响应速度和鲁棒性的滤波器时间常数。

利用内模控制器建立的内模控制系统架构图如图3所示。

图3 内模控制系统架构图Fig.3 Internal model control system architecture

图3中，系统的输出速度ω的计算过程为

3 实验结果

采用Matlab/Simulink作为软件平台，将AMD Ryzen5 3.4 GHz处理器、8 GB内存的Lenovo计算机作为硬件平台，对本文设计的内模控制器方法（Internal Model Controller Method，IMCM）和干扰观测器PID方法（PID Method of Disturbance Observer，PIDMDO）进行参考速度跟踪测试实验。实验中利用IMCM和PIDMDO两个方法分别对简单参考速度和复杂参考速度进行了跟踪实验，以测试不同方法的跟踪效果。

3.1 简单参考速度跟踪实验

采用阶跃变换的速度曲线作为简单参考速度曲线。利用IMCM和PIDMDO对所设置的简单参考速度曲线进行跟踪，其跟踪结果如图4所示。

通过分析PIDMDO和IMCM对简单参考速度的跟踪结果可以发现，图4（a）所示的PIDMDO方法跟踪结果，比图4（c）所示的IMCM方法跟踪结果波动更大，波动次数更多。以各方法对简单参考速度跟踪曲线中标记观察区为例，图4（b）所示的PIDMDO方法的跟踪误差，比图4（d）所示的IMCM方法的跟踪误差中，存在更频繁的波动，而且波动产生的超调量也较大。图4（b）中存在的最大超调量为8.625 rad/s，图4（d）中存在的最大超调量为6.375 rad/s。由此可见，本文设计的IMCM方法对简单参考速度具有更为准确和稳定的跟踪效果，能够控制直流伺服电机对阶跃变化的参考速度进行较好的跟踪。

图4 PIDMDO和IMCM对简单参考速度的跟踪结果Fig.4 Tracking results of PIDMDO and IMCM method for simple reference speed

3.2 复杂参考速度跟踪实验

采用曲线变换的速度作为复杂参考速度。利用IMCM和PIDMDO对所设置的复杂参考速度曲线进行跟踪，根据各方法的跟踪结果，分析其跟踪性能。IMCM和PIDMDO对复杂参考速度的跟踪结果如图5所示。

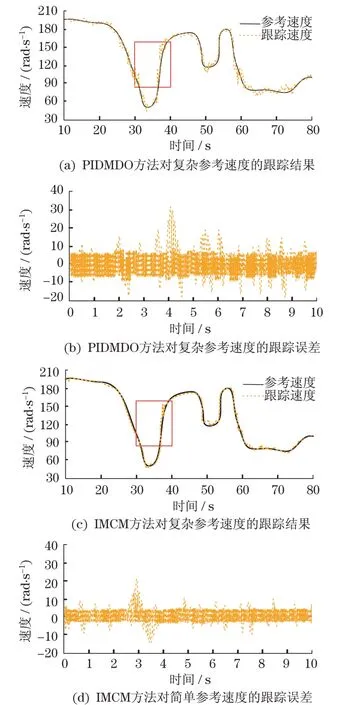
图5 PIDMDO和IMCM对复杂参考速度的跟踪结果Fig.5 Tracking results of PIDMDO and IMCM method for complexle reference speed

在图5（a）所示的PIDMDO方法对复杂参考速度的跟踪结果中，跟踪速度的曲线与参考速度的曲线较为贴合，但存在多次较大的超调现象。在图5（c）所示的IMCM方法对复杂参考速度的跟踪结果中，跟踪速度的曲线比图5（a）中跟踪速度的曲线更为贴合于参考速度的曲线，而且整个跟踪过程出现的超调次数较少，超调量也更小。以各方法对复杂参考速度跟踪曲线中标记观察区为例，图5（b）所示的PIDMDO方法对复杂参考速度的跟踪误差，比图5（d）所示的IMCM方法对复杂参考速度的跟踪误差中，含有更多的波动次数，而且波动量也更大。在图5（b）中最大超调量为32.483 rad/s，图5（d）中最大超调量为21.247 rad/s。由此说明，IMCM方法能够较好地适应曲线变化的复杂参考速度，能对其进行准确的跟踪。表明本文设计的IMCM方法不仅能够对直流伺服电机的速度进行更为准确的控制，而且其鲁棒性也较强，能够适应多种形式的参考速度。

4 结论

本文对直流伺服电机的模型进行了分析，明确了其电路平衡的计算过程，获取了其线性化机电动力学模型，得到了直流伺服电机对应的传递函数。在分数阶积分器传递函数的基础上，推导了其谱传递函数。利用CRONE控制方法的闭环传递函数，构造了内模控制器，并以内模控制器为依据，建立了内模控制系统，用以对直流伺服电机进行速度控制。实验结果显示：本文方法能够较好地对阶跃和曲线变化的参考速度进行跟踪，跟踪过程较为平稳和准确。说明本文方法可有效地对直流伺服电机的速度进行控制。