人车路径可达性评价方法综述

李真

（同济大学建筑设计研究院（集团）有限公司）

1 引言

可达性最早源于古典区位论，指对空间上某一要素实体（点、线或区域）的区位优劣程度进行的度量。1959年Hansen首次正式提出可达性，将其定义为“交通网络中各节点相互作用的机会大小”。同时，他利用重力方法研究了可达性与土地利用之间的关系[2]。从此时起，可达性开始广泛应用于城市规划、交通地理、区域和空间的研究中。

Bill Hillie（r1993）指出 ，60%的人行量和70%的车行量与城市网络模式有关，即路径的结构性因素在可达性的评价中具有关键的影响效应。那么，有哪些具体方法可以度量人车路径可达性，这些方法的适用性又是怎样的呢？

2 人车路径可达性的定义及评价方法

2.1 人车路径可达性的定义

2.1.1 人车路径

路径通常有两种理解，一种是指道路，有宽度、长度、品质、绿化和界面等属性；另外一种是指路线，即个体在时间和空间活动的连续轨迹。本研究中的人车路径，是指只包含路径的结构性属性，例如，长度、方向及其组成的网络等。

2.1.2 可达性

对可达性概念的理解主要有客观和主观两个方面：即空间可达性和心理可达性[3]。空间可达性又分为网络空间配置和空间上两点的相互作用。前者指到达网络中某点的难易程度[4]。度量方法一种是通过网络本身的属性得出可达性，另外一种是在路网基础上叠加物质功能的数量来推出的可达性。空间上点的相互作用的评价方法与交通网络空间形态无关，从地理学第一定律出发，是由两点间的引力规模定义出的可达性[3]。

文章研究的可达性是基于人车路径的结构性作用而形成的可达性，即空间网络可达性中的网络可达性，不考虑功能使用和人的心理因素等对其的修正作用。

2.2 人车路径可达性的评价方法

从路径角度出发的可达性评价方法，首先，运用图论，将交通网络归纳为几何网络或拓扑网络；然后，从以下五个视角来构建度量可达性的模型：空间阻隔、机会累积、空间作用、心理认知和拓扑连接[5]，也有这几种方法的集成和融合[6]。

通过对上述几种方法的总结，基于空间阻隔和拓扑连接的方法都包含从网络本身出发的可达性度量方法，而基于机会积累、空间作用和心理认知三种方法均是在路网基础之上加入了物质功能等其他因素后产生的综合可达性。因此，选择基于空间阻隔和拓扑连接两种视角下的可达性评价方法进行具体度量和研究现状的回顾。

3 人车路径可达性评价方法的研究现状

3.1 基于空间阻隔

19世纪50年代Pooler JA[7]最早提出了基于空间阻隔的可达性指标；Ingram[8]于1971年最早提出了这种方法的可操作模型，并且提出了相对可达性和综合可达性两个概念。相对可达性是一点和另外一点的空间阻隔；综合可达性是一点到区域中的所有点的空间阻隔的总和或均值。

Allen（1993）在综合可达性的基础上推导出整个网络的可达性[9]，该方法计算网络中的每一点到所有目的地点的平均距离，将此作为该点的可达性指标。由于在计算过程中用到矩阵，所以也称为矩阵法[3]。除了整体可达性矩阵，也有通过最短距离矩阵运算，获取节点和网络的可达性[10，11]。

基于空间阻隔的研究视角中，除了上述最基本的方法外，在实际应用中，也有三种相对简单的可达性度量方法。

1）直接距离测量法

这种方法顾名思义，直接利用物理距离来衡量可达性。Aultman Hall等(1997)在住区中选择了三个目的地（分别是学校、最近的公共空间、最近的地铁站），利用GIS测量了对于每个住户来说到达目的地最近的路径，在此基础上计算住户的平均步行距离、最大步行距离和最小步行距离，并统计出最小步行距离在400m以上的住户所占的比例[12]。这个测量方法用于案例之间不同地点的可达性比较。

2）距离比值法（PRD、Circuity factor）

这种可达性评价方法主要是利用基于路网的实际距离和两点间直线距离的比值来度量可达性。在步行路径可达性评价中，称之为步行非直线系数PRD（Pedestrian Route Directness），又称绕路系数。PRD值越接近1，可达性越好[13]，在城市尺度度量车行路径可达性时，这个比值被称为Circuity factor，在实际操作中可以用来估算城市间的实际出行距离[1]。

Hes（s1997）比较了处在城市不同区域的居住社区内部500f（t152m）、1000ft（304m）、1500f（t457m）、2000f（t610m）四种范围圈上的住户到达社区中心的PRD值，发现城市中心部位的密路网的住区可达性远比疏路网、尽端路多的城市边缘部位的可达性好；前者的PRD值为1.2，后者为1.7[13]。

波特兰（Portland）轨交站域的设计取PRD值作为设计街区尺度的备选标准之一，其上限是1.5[14]。Randall和Baetz发现方格网的街道邻里和相对小的街区PRD值大概是1.4-1.5；而曲线的道路和含有尽端路的街区则为1.63～1.88。同时，PRD值在1.2～1.5之间的街区可达性较好，如果该值达到了1.6～1.8，则说明这个街区有些绕路[15]。

3）面积比值法（PCA）

面积比值法主要是步行吸引区（Pedestrian Catchment Area）的方法，指从某一固定点出发实际步行5min（400m）或10min（800m）可达的面积与该点辐射的直线距离可达面积的比值[16]。PCA也被称为PED SHEDS，可以绘制一张步行实际范围图，从图1中可以很清晰地看出区域内到达邻里中心或者公交站点是否便利（见图1[17]）。这个指标具有很好的可视性，可精确估算区域的步行可达性[17]。

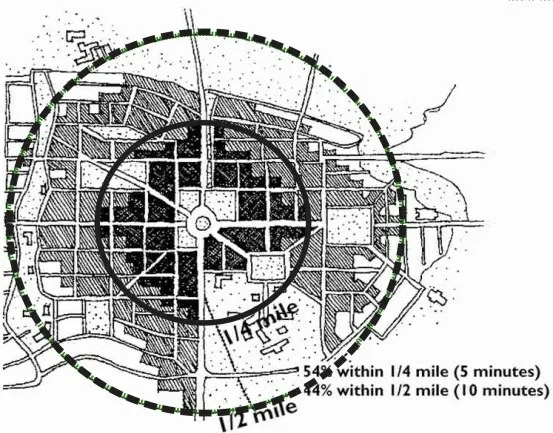
图1 PED SHEDS步行实际范围示意图

有研究指出，PCA值的指标如果达到0.6或者以上，就证明步行网络的可达性还不错，即大多数的理论可达区都可以通过实际的路网到达。PCA数值大于0.8则表明路网基本上是方格路网；如果PCA的数值小于0.3，则可以反映出这个区域的路网可达性非常不好[34]。

Schlossberg等人在2004年使用了PCA值对波特兰11个TOD地区的可达性进行了对比，在路网分类的情况下对几个地区的1993年和2002年TOD规划前后的PCA值分别进行了计算，发现PCA值都有所增高，说明在规划后该区域的可达性变好[18]。

3.2 基于拓扑连接

1）矩阵法

基于拓扑连接的矩阵法是将基于空间阻隔中的可达性计算公式中的物理距离替换成拓扑距离来计算。刘贤腾在一个抽象的城市分区模型基础上，利用城市各区域间的拓扑距离，举例计算了城市各个分区的综合可达性和标准化后的网络整体可达性，对比了整个城市不同区域之间的综合可达性[19]。陈洁等详细介绍了矩阵法基于拓扑距离的计算过程[3]。

2）空间句法

空间句法(space syntax)主要是利用轴线法（Axial）[20]、凸空间法（Convex）和可视性（Ⅴisibility）三种分析方法来对空间组构引起的活力进行研究。其中，轴线法较多地应用于线性空间，而视域法与凸空间法则更多应用在人的运动更具探索和即兴性质的非线性自由空间上。因此，在人车路径可达性评价中，一般采用空间句法中的轴线法，并且该方法已经有了较为成熟的研究成果。

在二维层面上，Bill Hillier等对空间整合度与人流量的关系进行了一系列研究发现，在伦敦，60%的人行与70%的车行量的不同与城市网络模式有关。在对伦敦King’s Cross车站区域及the City ofLondon两个案例进行轴线分析研究后发现，在局部整合度与人流的对数之间存在显著的相关度（R2=0.547）[21]；此外 ，通过对伦敦邦斯贝瑞（Barnsbury）区的实验研究，发现在人流的对数与局部整合度（R=3）之间存在很大的相关度（R2=0.734）[22]，这意味着大约有3/4的人流变化能够通过整合度值直接预测得出。

在三维层面，直接通过某个空间句法变量对人流量进行预测的能力会有所降低[21]。在D Chang及A Penn对伦敦巴比肯地区（Barbican）与南岸地区（South Bank）进行的人流量调研及句法计算与相关性分析中，发现引入一些空间变量，例如，出入口、垂直交通等，对整合度进行修正后，多层面空间系统的人流量将不再不可预测[23]。此外，王静文、朱庆、毛其智等人将空间句法与凯文·林奇的城市意向理论进行整合，通过对传统句法轴线图上存在意向点的区域进行整合度的加权修正，建立了一套句法三维扩展概念模型[24]。

近年来，空间句法也在轴线法（Axial）的基础上发展出了角度分析法（Angular），在2005年Bill Hillier和Shinichi Iida的文章中，通过四个城市空间的案例证明，空间句法的角度分析与人流量的相关性比轴线法与人流量的相关性更高[25]。

4 结语

基于路径的可达性评价方法中，主要是基于五种视角：空间阻隔、机会积累、空间作用、心理认知和拓扑连接，其中基于空间阻隔和基于拓扑连接的评价视角可仅从路径的角度对可达性进行评价。

在基于空间阻隔的可达性评价方法中，PRD法和PCA法都是衡量步行路径可达性的方法，前者适用于衡量节点之间的可达性，PCA法适用于衡量区域的总体可达性；circuity factor[1]则可以应用在城市两点之间的车行路径可达性的评价中；矩阵法不仅适用于网络中不同节点之间的可达性比较，也可以对路网的总体可达性进行评价。基于拓扑连接的可达性评价方法在步行和车行路径中均可应用。矩阵法在这里使用的是节点间的拓扑距离，应用于城际大尺度下的可达性评价中；空间句法中的轴线法（axial）在车行和人行中都有不错的预测结果，但在三维路网中，评价能力有所降低。近年来，角度分析法（Angular）在对路径人流的预测中，呈现出比轴线法（Axial）更好的研究结果，这需要用更多的案例进一步证明。