长距离地上输油管道保温层厚度设计

郭志阳,莫光贵,张天阳,刘子赫,李昌华,张学龄

1.长江大学石油工程学院,湖北 武汉 430100 2.中国石化管道储运公司,江苏 徐州 221008

管道保温层厚度直接影响到长距离输油管道保温效果。厚度不足引起热损失过大,原油温度低则黏度增大,易导致管道沥青和蜡析出堵塞管道等问题;厚度过大则材料费用和运行成本增加,造成管道包裹重量增加,不利于管道建设和保养的成本控制。因此如何科学设计管道保温层厚度,既能保障原油正常输送又能做到成本有效控制,正受到学术界和石油行业的广泛关注。

最大允许热损失法和外表面温度法是目前管道保温层厚度计算常用的设计方法。方立公[1]依照《设备及管道绝热设计导则》(GB/T 8175—2008)[2]中的最大允许热损失法计算了供热管道经济保温层厚度。考虑管路散热损失、供热介质沿途温降、管道表面温度及环境温度的作用,获取合理的供热管道保温材料及保温层厚度,降低了供热管道的散热损失,并减少了管道投资费用。李少华等[3]依照《设备及管道绝热技术通则》(GB/T 4272—2008)[4]中的外表面温度法计算了架空高温输油管道的保温层厚度。考虑管道周围的空气温度远小于管道内介质温度,结合保温后的年散热损失费用与保温工程投资的年分摊费用和最小的经济厚度,得到了架空高温输油管道保温层的最优结果,在减少保温层表面热损失量的同时降低了工程造价。罗树权[5]对DN200蒸汽管道的保温层厚度进行研究,通过最大允许热损失法计算了蒸汽管道保温层厚度。综合考虑架空敷设蒸汽管道的自然补偿以及热能价格和绝热结构单位造价的影响因素,得到合理经济的保温层厚度,减少了管道在输送过程中的散热损失,满足用户需求量以及冬夏季最大量和最小量的要求。在参照国标的研究中,由于没有考虑到温降的变化、流速的变化以及管道长度会对保温层厚度产生影响,忽略了环境因素(如风速和环境温度变化),导致计算结果与实际结果可能会存在一定误差。

允许温度降法是目前管道保温层厚度计算常用的设计方法。薛永明等[6]研究了长输蒸汽管道的温降计算方法,通过蒸汽温降的理论计算保温层厚度。考虑管道内径、流速、保温材料和蒸汽动力黏度等因素,确定长输蒸汽管道的经济保温层厚度。王振华[7]依照《工业设备及管道绝热工程设计规范》(GB 50264—2013)[8]中的允许温度降法确定了供热管道的保温层厚度，考虑管道内径与管内流速以及保温材料的影响因素,计算合理的保温层厚度,将散热损失控制在合理的范围之内。马明杰[9]针对某厂蒸汽管网保温效果存在的问题进行了研究,通过允许温度降法计算保温层厚度。考虑管道沿单位长度的热损失、管线的温降以及管线末端的温度,获取合理的保温层厚度,降低了管道输送时热量的损失。在参照国标的研究中,虽然考虑了温降、流速、热损失量以及环境温度的影响因素,但经验公式的取值相对固定,没有考虑到实际工况参数会随着管道流动发生变化,多方面的因素可能会导致设计精确度不高。付现桥等[10,11]横向比较了日本JISA9501、国际ISO12241和国标GB50254等标准之间的差异，对比认为国标大量简化了外表面换热、内外导热等因素的模型,未能较好地反映真实的传热过程特性,同样条件下设计管道保温层厚度远远厚于其他标准。

对针现状,笔者建立了考虑管道及保温层内外膜阻、外部空气对流换热及管道与保温层传热的综合有限元模型；以管道出口温度即允许温度降为目标,利用二分迭代方法求解,获取了长度为300km、入口温度50℃、出口温度35℃的地上输油管道保温层的最小厚度；讨论了保温层导热系数、管道内径和管道流量3个因素对最小保温层厚度的影响。

1 管道保温层传热有限元模型

描述管内原油的连续性方程和动量方程分别为：

▽(Aρu)=0

(1)

(2)

式中：A为管道横截面积,m2;ρ为原油密度,kg/m3;u为管道曲线切向的流动速度,m/s;p为管内油压,N/m2;dh为管道直径,mm;fD为达西摩擦因子,1。

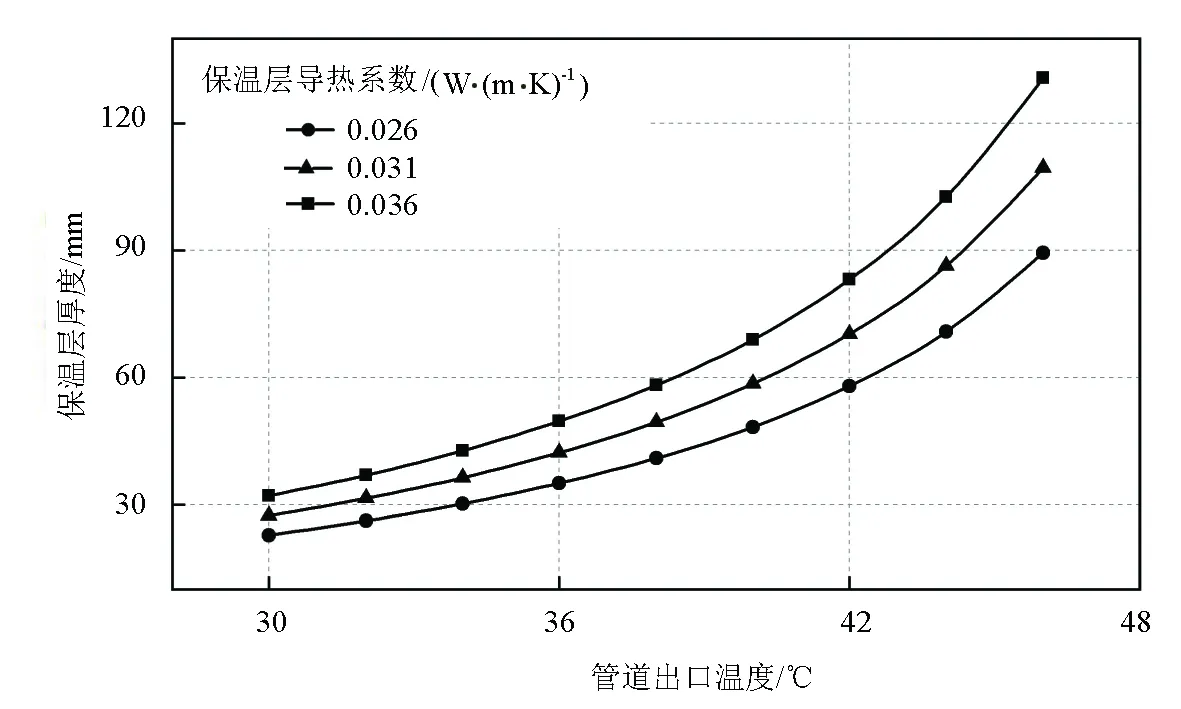
由于密度变化微小可以忽略不计,通常会在建模中不考虑重力的影响。式(2)中描述了由于原油内部剪切黏度引起的压降,达西摩擦因子fD是根据Haaland方程[12]计算的,对于较大的雷诺数范围(4×103

管道表面粗糙度e满足：

(3)

原油的雷诺数Re：

(4)

能量方程式为：

(5)

管壁与周围环境进行热交换而产生的热损失Qwall计算式为：

图1 管壁传热阻力示意图 Fig.1 Schematic diagram of wall heat transfer resistance

Qwall=hZ(Text-T)

(6)

式中：e为管道表面粗糙度,mm;Re为流体的雷诺数,1;uext为原油平均速度,m/s;μ为原油黏度,Pa·s;Cp为恒定压力下原油的比热容,J/(kg·K);T为原油温度,K;k为导热系数,W/(m·K);Qwall为管壁与周围环境进行热交换而产生的热损失,W/m2;h为总传热系数,W/(m2·K);Z为管道湿周,即过流断面上流体与固体壁面接触的周界线,m;Text为管道外部环境年平均温度,K。

假定管道周围的温度不变,并且通过管壁的热传递是准静态的。壁传热阻力示意图如图1所示。

对于此类圆管,hZ的有效值计算公式为：

(7)

图2 管道横截面示意图 Fig.2 Schematic diagram of pipeline cross section

对于只存在一层管壁和一层保温层的管道,可以简化为金属管道壁厚为10mm,保温层导热系数为2.60×10-2W/(m·K),管壁导热系数为46.5W/(m·K)单层管壁和单层保温层的管道,如图2所示。

管道内部薄膜传热系数hint计算公式为：

(8)

管道内部努塞尔数Nu[13]int计算公式为：

(9)

(10)

根据Gnielinski公式[14]可知,式(9)适用于管道内部强制对流传热计算。

管道外部空气流动引起的管道外部薄膜传热系数hext计算公式为：

(11)

管道外部努塞尔数Nuext计算公式为：

(12)

根据Churchill-Bernstein准则[15]可知,式(12)适用于管道外部强制对流传热计算。

这个单相强制对流传热的模型已经有很多文献[13-19]对其进行了论述,直接利用其一般格式和对应的流速/尺寸等参数代入建立的有限元数值模型。综上,利用上述数学模型建立了考虑管道内外膜阻和保温层外部空气对流换热的有限元模型。以出口温度Ts为收敛条件,利用二分法[20]迭代求解最小保温层厚度,直到结果满足相对误差判定：

(13)

式中：(hZ)eff为有效的hZ值;r0为管道内径,mm;rn为n号管壁外半径,mm;rn-1为n-1号管壁外半径,mm;rN为N号管壁间层外半径,mm;kn为n号管壁的导热系数,W/(m·K);hint为管道内部薄膜传热系数,W/(m2·K);hext为管道外部薄膜传热系数,W/(m2·K);koil为原油导热系数,W/(m·K);kair为空气导热系数,W/(m·K);Nuint为管道内部努塞尔数,1;Nuext为管道外部努塞尔数,1;Pr为普朗特数,1;Tc为计算的出口温度,℃;Ts为设定的出口温度,℃。

2 模型结果讨论

利用上面控制方程的弱形式建立一维有限元模型。建立的模型基本参数如下：划分为300个基于三次Hermite插值的单元,管道内径为590mm,管道长度为300km,壁厚为10mm,设计流量为1500m3/h。对非等温管道流进行稳态研究,求解流体流动和温度耦合,入口边界为流量入口,出口边界为温度出口。对流体流动、传热和质量传递进行模拟,把管道中每一段流体都假设为充分发展的状态,运用管道内流动的动量、能量和质量守恒定律,获取沿管道长度的沿程摩擦损失以及黏性热效应,通过耦合计算出管道保温层厚度。管道相关参数如表1所示。

表1 管道主要相关参数

目前长距离地上输油管道保温层厚度标准化设计主要依据为《工业设备及管道绝热工程设计规范》(GB 50264—2013)[8]。允许温度降法从管道两端温度变化入手,结合保温材料、管道内径、管道长度、原油流量的影响,经计算保温层厚度为61.1mm。模型以国标中温度降法计算保温层厚度61.1mm为计算初值,以出口温度35℃为收敛条件,利用二分法迭代求解最小保温层厚度。

图3和图4分别为保温层厚度迭代求解及相对误差降低过程。经13次二分法迭代,相对误差为0.007%，满足式(13)要求，求解得到的最小保温层厚度为32.48mm,小于国标设计结果61.1mm。二者差异主要由2个方面组成：①国标设计忽略了原油流动内摩擦产生的热量能够抵消一部分热损失量,而有限元设计不仅考虑了管道及保温层内外膜阻和黏度的影响,还考虑了流速的变化会引起热量随之变化[21];②国标计算是建立在工程经验方程基础上的,计算结果通过安全系数修正而导致偏保守,而笔者建立的有限元模型对摩擦、导热和对流等过程描述精细。

矿山生产活动可能会形成地质灾害隐患，区域性的应力、应变日积月累，加之降雨等诱发性外部因素影响，应力、应变累积量超越临界点，就可能产生滑坡、沉塌、塌陷等地质灾害。伴随着科学技术发展，矿山监测监控物联网已逐渐替代传统的人工观测、计算方式，可对地质灾害隐患进行全天候、实时在线监测监控，自动生成监测监控数据、图像等成果资料，为防灾减灾提供科学依据。

图3 保温层厚度迭代求解 图4 相对误差降低过程Fig.3 Iterative solution of insulation thickness Fig.4 Relative error reduction process

当保温层厚度为32.48mm时,300km管道中温度分布如图5所示。同时利用有限元模型计算了无保温层厚度和GB 50264—2013要求的61.1mm保温层厚度时,相应的管道温度分布。管道出口温度与管道长度关系如图5所示。

图5 不同保温层厚度的管道出口温度与管道长度关系Fig.5 Relationship between outlet temperature and length of pipeline with different insulation thicknesses

由图5可知,随着管道长度的增加,原油温度逐步降低。其中考虑原油内外膜阻而无保温层厚度时,管道出口温度为8.14℃,略高于环境温度,当不考虑原油内膜阻而无保温层厚度时,管道出口温度为8.09℃,接近环境温度。这是因为原油内摩擦做功将会提高原油温度。有限元方法求解的保温层厚度32.48mm时管道出口温度为35℃,利用模型评估GB 50264—2013中获取的保温层厚度求得管道出口温度为42.56℃。虽然满足管道保温要求,但加重了管道重力载荷,增加了保温费用,不利于维护作业与成本控制。随着管道长度的增加,在0～300km,有保温层时,管道出口温度近似直线降低,这表明热损失的主要形式为热传导,流体内摩擦的作用并不能直接判断;在0～150km,无保温层时管道出口温度变化近似指数降低,这说明此时管道受到热传导和热对流共同作用明显降低温度;而大于150km时,温度均只比环境温度略高,由温度梯度造成的热量基本完全从原油到环境的传递。考虑原油内外膜阻而无保温层时,出口温度略高于不考虑内膜阻情况,温度差异主要由内摩擦做功造成,而差异较小是因为金属管道的热扩散系数较大导致。每日输送原油内能的变化为：

Q=CρqvtΔT

(14)

式中：Q为热量,kJ/d;C为原油比热容,J/(kg·℃);qv为体积流量,m3/h;t为时间,h;ΔT为吸热前后的温度差,℃。

由摩擦做功产热在温度度量上是比较小的数值,但是在能量度量上还是一个很重要的因素。最大温度变化见图5,分别是0.876、1.132、0.587℃。即根据式(14)可换算得到原油输送摩擦做功生热产生的能量,取C=2000J/(kg·℃),ρ=843kg/m3,qv=1500m3/h,t=24h,ΔT1=0.876℃,ΔT2=1.132℃,ΔT3=0.587℃,可知热量Q1=5.32×107kJ/d,Q2=6.87×107kJ/d,Q3=3.56×107kJ/d。热能主要来自输送泵的耗能,这部分能量的估算对于泵的选型具有一定的参考。在保温层设计时,应注意能量效率对温度变化的敏感性。

3 影响保温层厚度的因素

为了解不同管道出口温度要求下,管道保温层厚度受保温材料导热系数、管道内径和管道流量影响,利用上述有限元模型做了进一步的数值模拟分析。所有算例中入口温度为50℃,出口温度分别为30～46℃,其他参数设置与前面模型相同。

3.1 保温层导热系数

图6为不同导热系数及对应出口温度要求下保温层厚度计算结果。由图6可知,随着管道出口温度的增加,保温层厚度逐步增加。当出口温度为30℃,保温层导热系数为0.026、0.031、0.036W/(m·K)时,对应的最小保温层厚度分别为22.76、27.36、32.04mm。当导热系数为0.036W/(m·K),出口温度为46℃时,保温层厚度达到了130.74mm。此时,管道整体直径达到了851.48mm。但工程中,过厚的保温层会导致重力与风载荷急剧增加,不利于保障管道强度。在各设定出口温度的条件下,随导热系数增大保温层厚度快速增加,加强了保温层的热传导而只能增加厚度降低热量的损失[22-25]。

图6 不同导热系数的保温层厚度与管道出口温度关系 Fig.6 Relationship between insulation thickness and outlet temperature of pipeline with different thermal conductivities

3.2 管径

图7为不同管径及对应出口温度要求下保温层厚度计算结果。由图7可知,随着管道出口温度的增加,保温层厚度快速增加。当出口温度为30℃,管径分别为600、700、800mm时,对应的保温层厚度最小,分别为23.74、32.78、40.58mm。当管径为800mm,出口温度为46℃时,保温层厚度达到270.29mm,管道整体直径达到了1340.58mm。此时保温层的导热系数虽然不高,但原油与管道接触面积增大且与热交换时间大大增加,导致热传导温度损失增加。同时管径增加导致保温层与空气对流换热的面积也增加。原油流速降低,其内摩擦力减小,相应的做功降低,三者共同作用使得能量损失更大,因而保温层厚度急剧增加[22-25]。

图7 不同管径的保温层厚度与管道出口温度关系 Fig.7 Relationship between insulation thickness and outlet temperature of pipeline with different pipe diameters

3.3 管道流量

图8为不同管道流量及对应出口温度要求下保温层厚度计算结果。由图8可知,随着管道出口温度的增加,保温层厚度逐步增加。当出口温度为30℃,管道流量为1300、1400、1500m3/h时,对应的最小保温层厚度分别为28.94、25.62、22.76mm。当管道流量为1300m3/h时,出口温度为46℃,保温层厚度达到了127.31mm。当管道流量为1500m3/h时,出口温度为46℃,保温层厚度达到了89.42mm。在同一出口温度时,随管道流量的增大保温层厚度降低,这主要由于流速较大时,原油与管壁直接接触时间降低,热传导时间变短,同时做功随着原油内摩擦阻力增加而增加,导致自身升温。计算结果表明,原油内摩擦阻力做功产热对原油运输温度保障必须仔细考量[22-25]。

图8 不同管道流量的保温层厚度与管道出口温度关系 Fig.8 Relationship between insulation thickness and outlet temperature of pipeline with different pipeline flow rates

4 结论

建立了基于有限元方法的原油管道传热保温模型,可以计算管道内外膜阻、外部空气对流换热及管道与保温层传热问题,是对GB 50264—2013经验模型设计管道保温层厚度方法的补充,进一步利用该模型深入讨论了保温层导热系数、管道内径、管道流量3个因素对保温层厚度的影响。

1)由于模型考虑了管道的传热模型,并且考虑了原油内摩擦做功产热,因而较现有标准更准确。如在对比算例中,GB 50264—2013设计的保温层厚度过厚,与有限元模型有一定差异,结果说明现行标准可能存在保守的经验设计环节。

2)参数研究时发现,保温层导热系数对管道的热传导影响较大;管径增大对热传导、热对流及原油摩擦产热都有抑制,这导致了保温层厚度快速增加;而管道流量增加则更多影响原油与管壁热交换时间并增加原油内摩擦做功产热。因此在工程实践中,应综合考量保温层导热系数(即材料)、管径与管道流量的设计,平衡三者与热传导和热对流之间的关系。

3)笔者并未考虑工程造价成本与各参数关系,建议使用参考有限元模型设计管道保温层厚度时,可与管道建设成本等统筹优化。