考虑宽应变率的修正Johnson-Cook模型及蜂窝板动态力学响应模拟
2021-07-08李双蓓常岩军
李双蓓,赵 璇,吴 园,常岩军
( 1. 广西大学土木建筑工程学院,广西 南宁,530004;2. 广西大学工程防灾与结构安全教育部重点实验室,广西 南宁,530004;3.广西大学广西防灾减灾与工程安全重点实验室,广西 南宁,530004)
金属蜂窝板是由蒙皮、胶层和蜂窝芯层组成的夹层结构,凭借其比强度高、抗冲击性能好等优点而广泛应用于建筑幕墙、室内装饰、车辆船舶等领域,近年来,该结构在动荷载下的力学研究已成为相关领域的热点[1-2],尤其数值仿真技术的不断进步,不仅突破了传统实验研究手段的局限[3],还能明显提高分析效率,而仿真结果的精确程度则直接取决于材料本构模型的正确与否。
通常,在冲击荷载作用下,金属材料的应变率变化范围较宽,低、中、高3种应变率阶段均会出现。Johnson等[4]通过分析实验数据,总结出应变率效应项、应变硬化项及温度项乘积形式的Johnson-Cook经验型本构模型(JC模型),该模型因具有物理意义清晰、参数易标定等优点而成为分析金属材料动态响应的主流模型,但其缺陷在于不能同时满足金属宽应变率下的本构关系,因此需对模型进行修正[5-6]。在修正JC模型应变率效应项方面,孟利平等[7]使用Cowper-Symonds(CS)应变率强化模型[8]替换JC模型中的应变率项从而获得了能够更好表达应变率强化效应的JC-CS模型;Kang等[9]将JC模型中的1次应变率效应项修正为高阶应变率效应项,所得修正模型更适用于描述车身在高速碰撞下的动态响应;Huh等[10]在JC模型中添加2次应变率效应项后,模型预测值与实验数据虽仍有一定差距,但二者偏差较之前明显减小。此外,因为高应变率下金属的应变硬化特征会发生显著变化,所以金属在不同应变率阶段所遵循的应变硬化准则也不尽相同[5]。在对JC模型应变硬化项进行修正时,Kim等[11]提出的H/V-R模型线性组合了Hollomon模型[12]和Voce准则[13],能够较为准确地反映钢材动态行为随应变率提高而变化的现象,但由于该模型具有高度非线性性质,加之材料参数设置也存在一定局限性,因此难以准确估计不同应变率条件下的材料应力-应变关系,不利于实际工程应用;李营等[14]修正后的线性叠加模型以应变1次项和2次项的和为应变硬化项,研究表明,该模型以加和形式虽然提高了对金属行为预测的能力,但拟合所得曲线接近于一次函数,与实测值变化的趋势差异较大。综上可知,仅仅通过修正JC模型中的应变率效应项或应变硬化项均不能有效提高模型在宽应变率条件下的适用性。有鉴于此,本文拟对常温下的JC本构模型应变硬化项和应变率效应项进行修正,提出适用于宽应变率条件的H/V-CS本构模型并对模型的正确性进行验证,再通过显式VUMAT接口将H/V-CS本构模型导入ABAQUS有限元分析软件中,建立冲击荷载作用下的蜂窝板结构模型,进而基于该模型分析蒙皮厚度、芯层壁厚和芯层高度等因素对蜂窝板吸能效果的影响,以期为建立更符合实际的宽应变率金属动态本构关系及蜂窝板在实际工程中的防护和优化提供参考。
1 宽应变率下H/V-CS金属动态本构模型
1.1 H/V-CS本构模型的建立
1.1.1 JC本构模型
JC本构模型是被广泛应用的一种唯象型动态本构模型,将金属材料的真实应力直观地表示为应变硬化、应变率修正项和温度项的乘积,当不考虑温度效应时,其基本形式为:
(1)
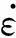
1.1.2 应变硬化项修正
大多数金属材料在不同应变率下所表现出的硬化规律并不一致,所遵循的准则往往随着应变率的增大由Ludwik准则[15]转变为Voce准则,这主要是因为Ludwik准则为幂函数形式,真实应力随真实应变的增加而不断增大,而Voce准则为指数型,应力在大应变条件下会不断接近饱和状态,即应力-应变曲线会出现水平渐近线[5],这与实际高应变率条件下金属材料真实应力会随应变的增大而趋于饱和的现象[16]一致,故Voce准则更适于展现金属材料在高应变率下的本构关系。
Kim等[11]和李营等[14]针对硬化规律对JC本构模型的应变硬化项进行改进,相应得到H/V-R模型和线性叠加模型分别如式(2)和式(3)所示:
(2)
(3)
式(2)~式(3)中,α1、α2、m1、m2、a1、a2、P及q均为材料常数;σ0为静态真实应力;fH表示Hollomon准则,引入初始屈服强度值后发展成为Ludwik准则,fV表示Voce准则,二者表达式分别为:
fH=Bεn
(4)
fV=A2-Dexp(-Eε)
(5)
式(5)中,A2为材料常数;D为金属强度系数;E为硬化指数(Voce硬化准则),可通过拟合金属真实应力-应变关系而得到。
为了准确描述金属材料在不同应变率阶段的应变硬化性质,本文参考H/V-R模型(式(2))及线性叠加模型(式(3))对应变硬化项的处理方式,根据真实应力-应变曲线特征,将Ludwik准则与Voce准则叠加获得新的应变硬化项,表达式为:
σ=A+Bεn-Dexp(-Eε)
(6)
式中,A为材料常数。
1.1.3 应变率项修正
利用CS模型[8]可获得材料动态真实应力与应变率之间的关系表达式为:
(7)
式中,σd为动态真实应力;C和m为材料常数。
以文献[14]所报道的船用低碳钢、文献[17]所报道的921A钢以及文献[18]所报道的EH36钢为研究对象,分别利用JC模型应变率效应项和CS应变率强化模型获得上述钢种的屈服强度-应变率关系拟合曲线,并将拟合值与相应文献所提供的实验值进行比较,结果如图1所示。从图1
中可以看出,利用JC本构模型应变率效应项对船用低碳钢及921A钢力学行为进行拟合时,在中、高应变率阶段所得数据与相应实验值差异较大,而利用CS模型所得3种钢的拟合结果均与相应实验值吻合度较高,兼顾了材料在低、中、高应变率阶段的力学行为变化,满足宽应变率的要求。因此,本文选择CS模型作为金属材料本构模型中的应变率效应项。
1.1.4 H/V-CS本构模型
将修正后的应变硬化项与CS模型应变率效应项耦合,获得适用于宽应变率条件的H/V-CS本构模型,表达式为:
(8)
由式(8)可见,该本构模型表达式中的参数较H/V-R模型(式(2))更少,模型应变硬化项考虑了金属在不同应变率范围内的真实应力-应变关系,包容性较强,拟合方式也较为灵活。同时,模型选用更能准确反映应变率敏感性的CS模型作为应变率强化项,考虑了金属材料的应变率效应,使得整个模型能够充分体现金属材料的力学性能,物理意义清晰,具有通用性。
1.2 H/V-CS本构模型参数的确定
本文基于文献[5]所报道的Q420钢拉伸实验和文献[19]所报道的2024-T3铝的霍普金森拉杆实验,对JC模型及本文所提H/V-CS模型在宽应变率条件下的适用性进行讨论,这2种金属材料分别广泛应用于建筑及航空领域,应变率变化涵盖低、中、高3个阶段,具有一定的普适性。
首先选用数值优化仿真计算软件平台First Optimization(1stOpt)中的全局优化算法,再编写程序输入待拟合参数的模型表达式以及不同应变率下真实应力-应变实验数据,无需依赖初值,即可得到2种材料的H/V-CS模型参数如表1所示。

表1 H/V-CS本构模型参数
待获得H/V-CS模型参数后,再分别使用JC模型和H/V-CS模型对Q420钢及2024-T3铝在多种应变率条件下的应力-应变关系进行预测,将所得理论模型预测结果与相应文献所提供的实验值进行对比,结果如图2所示。由图2可知,2种金属材料在不同应变率条件下都表现出明显的应变率强化效应。当使用JC模型对金属材料的应力-应变关系进行预测时,高应变率条件下的模型预测值与实验实测值差异较大,如图2(a)中应变率分别为133、288 s-1条件下的2条模型预测曲线大部分重叠,未表现出应变率敏感性,且预测值与相应的实验值存在明显偏差,这种现象在图2(b)中(应变率为0.01、500、1300 s-1)表现得更为明显,应归因于JC模型所采用的应变硬化准则和应变率强化项更适用于中、低应变率条件,对金属材料高应变率阶段的力学行为变化不够敏感,难以真实反映金属材料的应力-应变关系,所以在宽应变率条件下使用JC模型不能准确预测金属材料的应力-应变关系;当使用H/V-CS模型对金属材料应力-应变关系进行预测时(图2(c)~图2(d)),2种金属材料在低、中、高应变率条件下的模型预测结果均与相应实验值高度吻合,体现了该模型在宽应变率条件下的适用性与准确性,由此可证明在宽应变率条件下,将Voce模型和Ludwik模型组合的应变强化模型耦合CS应变率强化模型后,所得H/V-CS模型可以更好地表达金属材料的应变率敏感性,对金属材料应力-应变关系的预测结果符合相应的真实发展趋势。
(a) 船用低碳钢 (b) 921A钢 (c) EH36钢
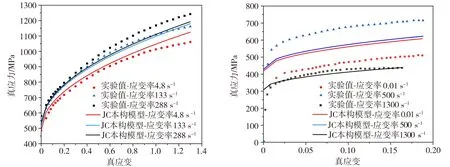
(a)Q420钢,JC本构模型 (b)2024-T3铝,JC本构模型
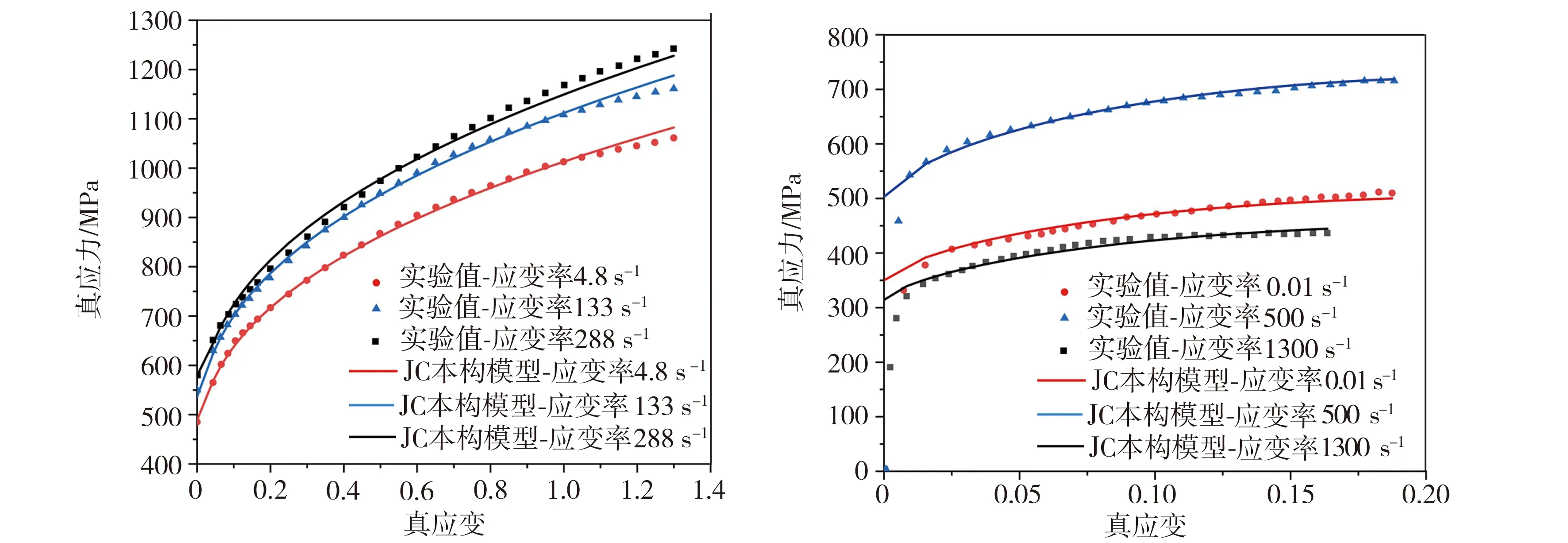
(c)Q420钢,H/V-CS模型 (d)2024-T3铝,H/V-CS模型
1.3 H/V-CS本构模型VUMAT开发
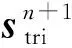
(9)
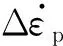
(10)
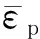
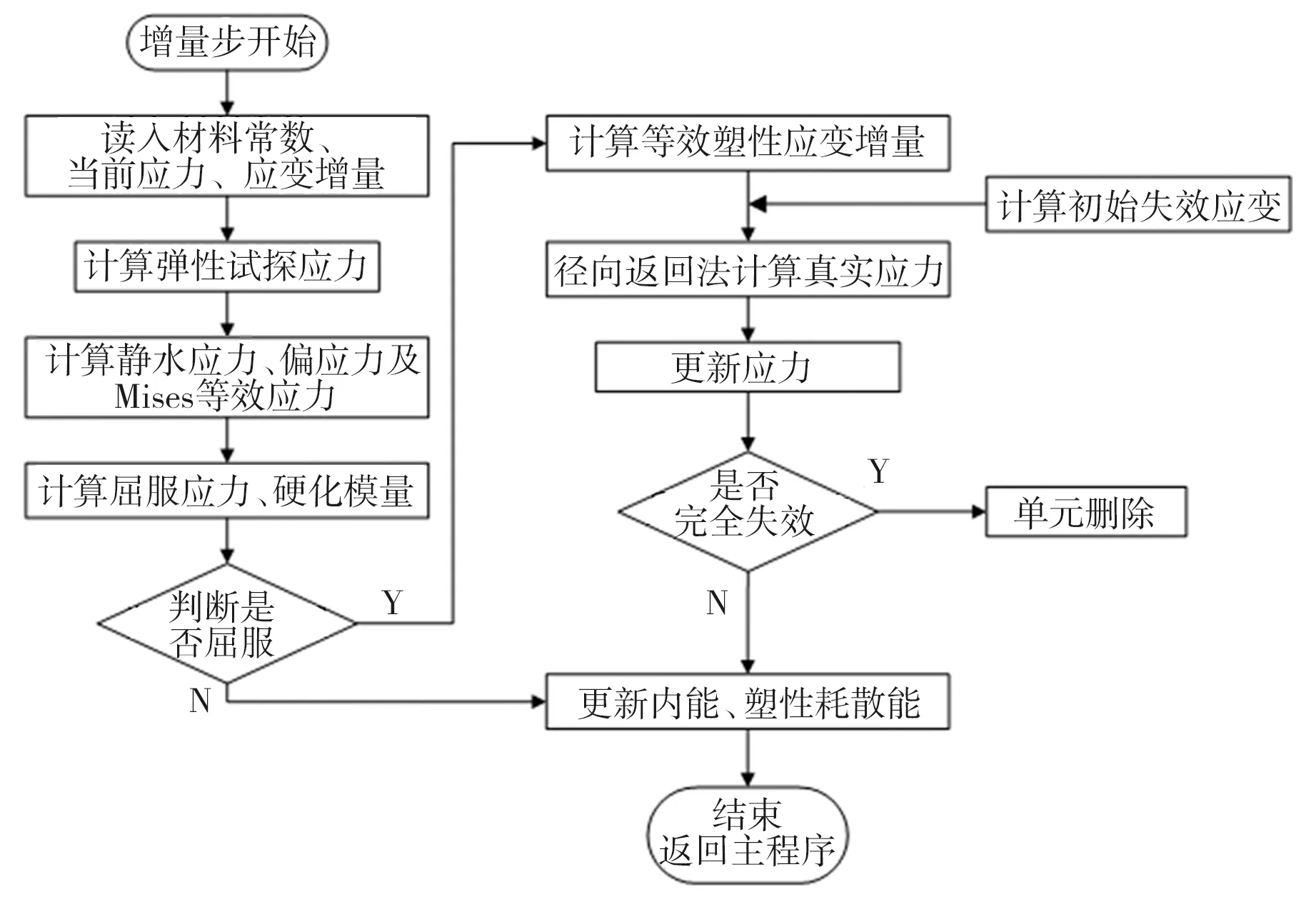
图3 VUMAT子程序流程图
2 基于H/V-CS本构模型的蜂窝板动态力学响应模拟
2.1 蜂窝板模型的建立与验证
为验证VUMAT子程序的正确性,本文以蜂窝夹层板为研究对象,参照文献[2]建立模型,该结构如图4所示,其中蒙皮厚度Tf为1 mm,蜂窝单元直径R为6.35 mm,蜂窝芯层高度h为18mm,蜂窝芯层厚度tc为0.07 mm,蒙皮(2024-T3铝材质)的H/V-CS模型参数见表1,其余部件属性均参照文献[2]设定。采用ABAQUS有限元软件构建蜂窝板有限元模型(见图5)并模拟蜂窝板冲击试验(冲击能为81.07 J),获得冲击中心点处沿X、Y、Z方向的应变率时程曲线如图6所示。由图6可见,冲击点处沿不同方向的应变率均变化复杂且无规律,应变率值覆盖了低、中、高3个阶段,故采用传统的动态本构模型难以满足精确计算的要求,在此基于本文所提H/V-CS宽应变率动态本构模型,借助ABAQUS软件对蜂窝板在不同冲击能下的冲击过程进行模拟,将蜂窝板损伤深度模拟计算值与文献[2]所提供的相应的实验值进行对比,结果如图7所示。由图7可见,在不同冲击能量条件下,由ABAQUS模拟计算所得蜂窝板损伤深度均与相应实验结果基本一致,最大误差不超过5%,从而验证了H/V-CS本构模型与有限元仿真模型的准确性,因此可利用这两个模型进一步探究蜂窝板结构参数对蜂窝板在冲击荷载下吸能效果的影响。
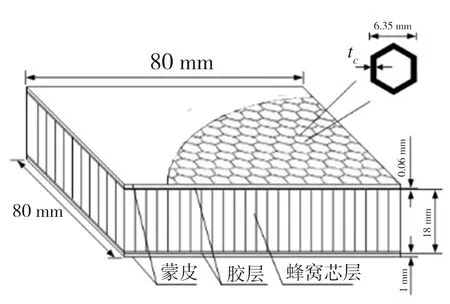
图4 模型结构
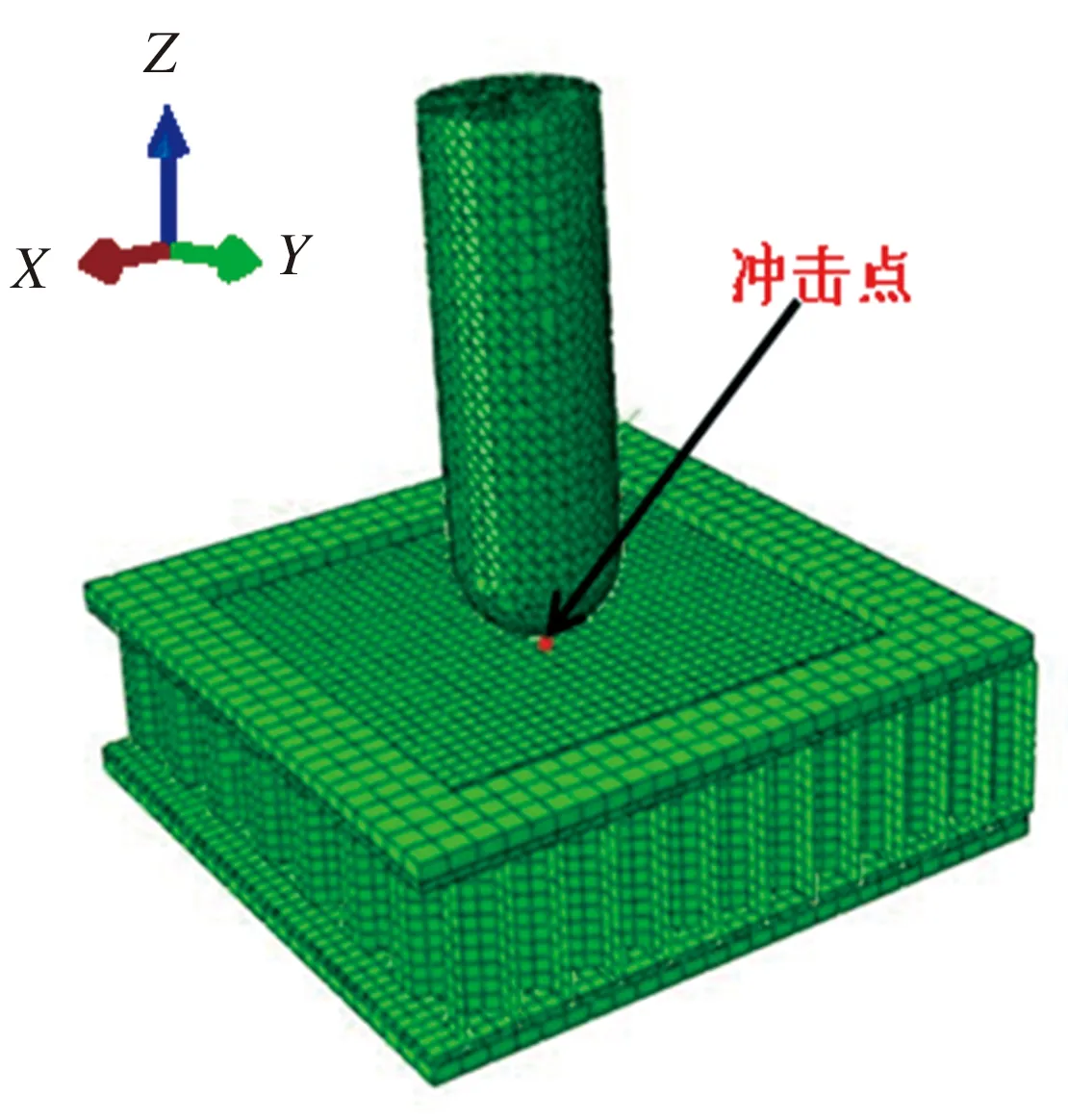
图5 蜂窝板有限元模型
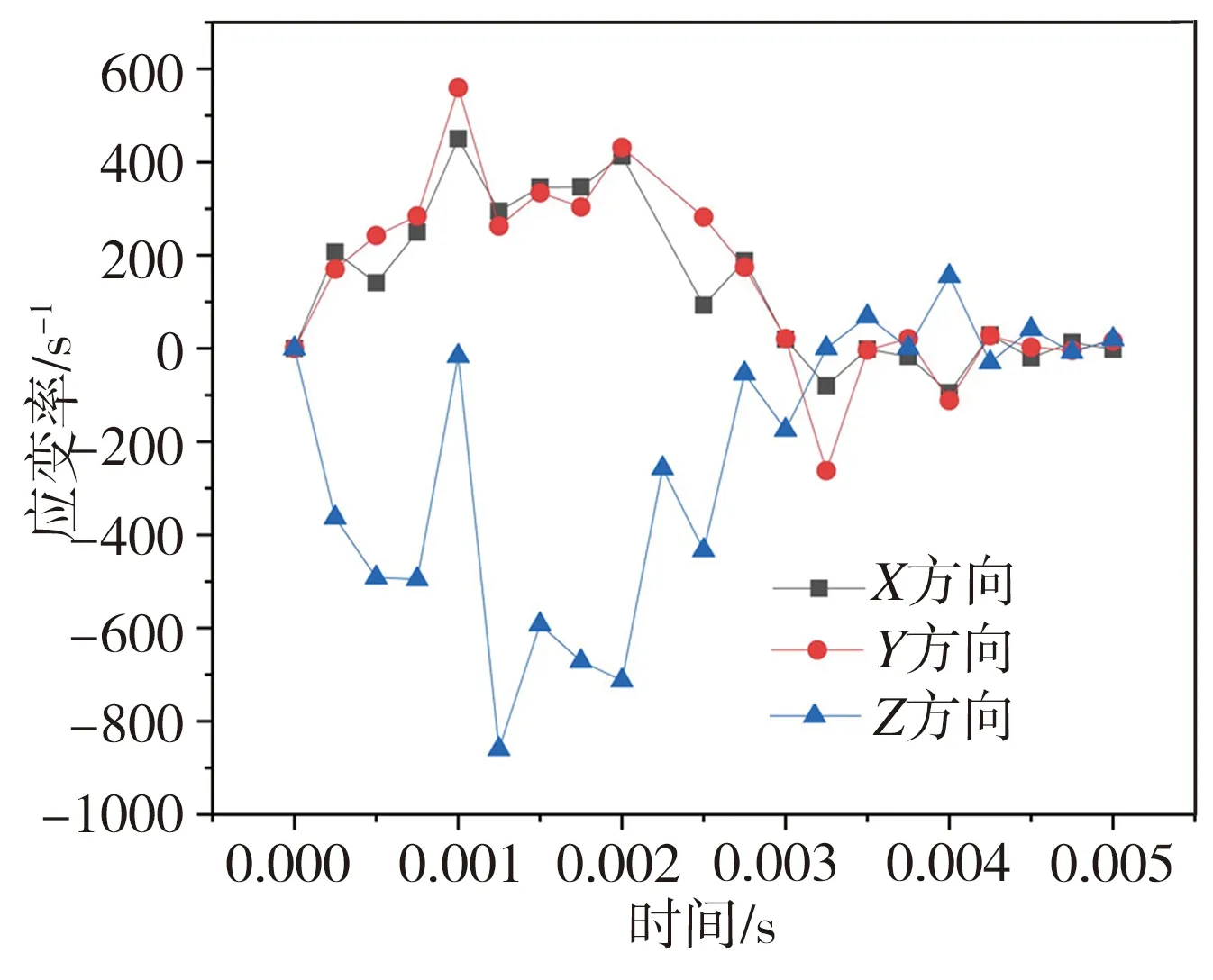
图6 应变率时程曲线
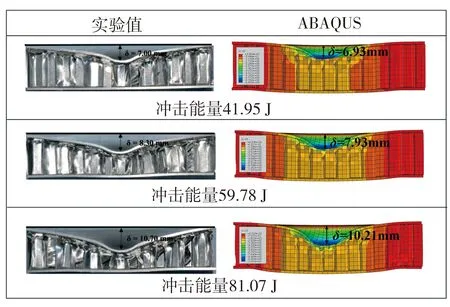
图7 蜂窝板损伤深度
2.2 蜂窝板结构参数对其吸能效果的影响
设定圆柱体平头弹底面半径为10 mm,高为56.7 mm,保持冲击能量为81.07 J,利用本文所构建的H/V-CS本构模型与有限元仿真模型研究了蜂窝板遭受平头弹冲击时,蒙皮厚度(0.5、1.0、1.5 mm)、蜂窝芯壁厚(0.035、0.07、0.105 mm)以及蜂窝芯高度(9、18、27 mm)等结构参数对其吸能效果的影响,分析结果见图8,相应条件下蜂窝板的吸收能量稳定值如表2所示。由图8(a)可见,当蒙皮厚度分别为0.5、1.0、1.5 mm时,相应的蜂窝板吸收全部能量的时长依次为4.2、3.2、2.8 ms,吸能速率随蒙皮厚度的增加而增大,因此,增加蒙皮厚度可有效提高蜂窝板吸能效果;由图8(b)可见,当蜂窝芯壁厚分别为0.035、0.07、0.105 mm时,相应的蜂窝板吸收全部能量的时长依次为8.7、3.2、2.5 ms,吸能速率随蜂窝芯层壁厚的增加而增大,并且还需指出的是,较薄的蜂窝芯层将导致蜂窝板刚度严重降低;由图8(c)可见,当蜂窝芯高度分别为9、18、27 mm时,相应的蜂窝板吸收全部能量的时长依次为4.0、3.2、2.9 ms,吸能速率随蜂窝芯高度的增加而增大,蜂窝芯的高度变化对其吸能效率也有较明显的影响;从表2中可以看出,蜂窝板吸收能量稳定值随蒙皮厚度或蜂窝芯壁厚的增加而减小,并随蜂窝芯高度的增加而增大。这表明蜂窝板结构参数对蜂窝板力学行为的影响在变化程度和变动方向上均有体现,因此实际工程中在对蜂窝结构进行优化和使用时,需谨慎考量材料参数、结构性能和功能需求之间的关系。
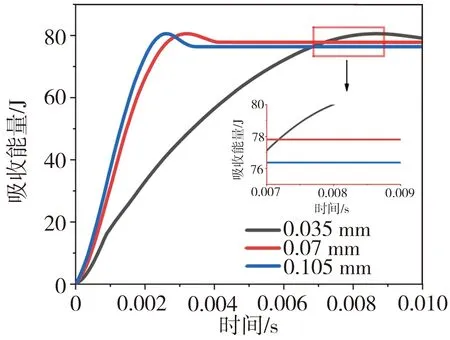
(b)蜂窝芯壁厚(蒙皮厚度、蜂窝芯高度分别为1.0、18 mm)
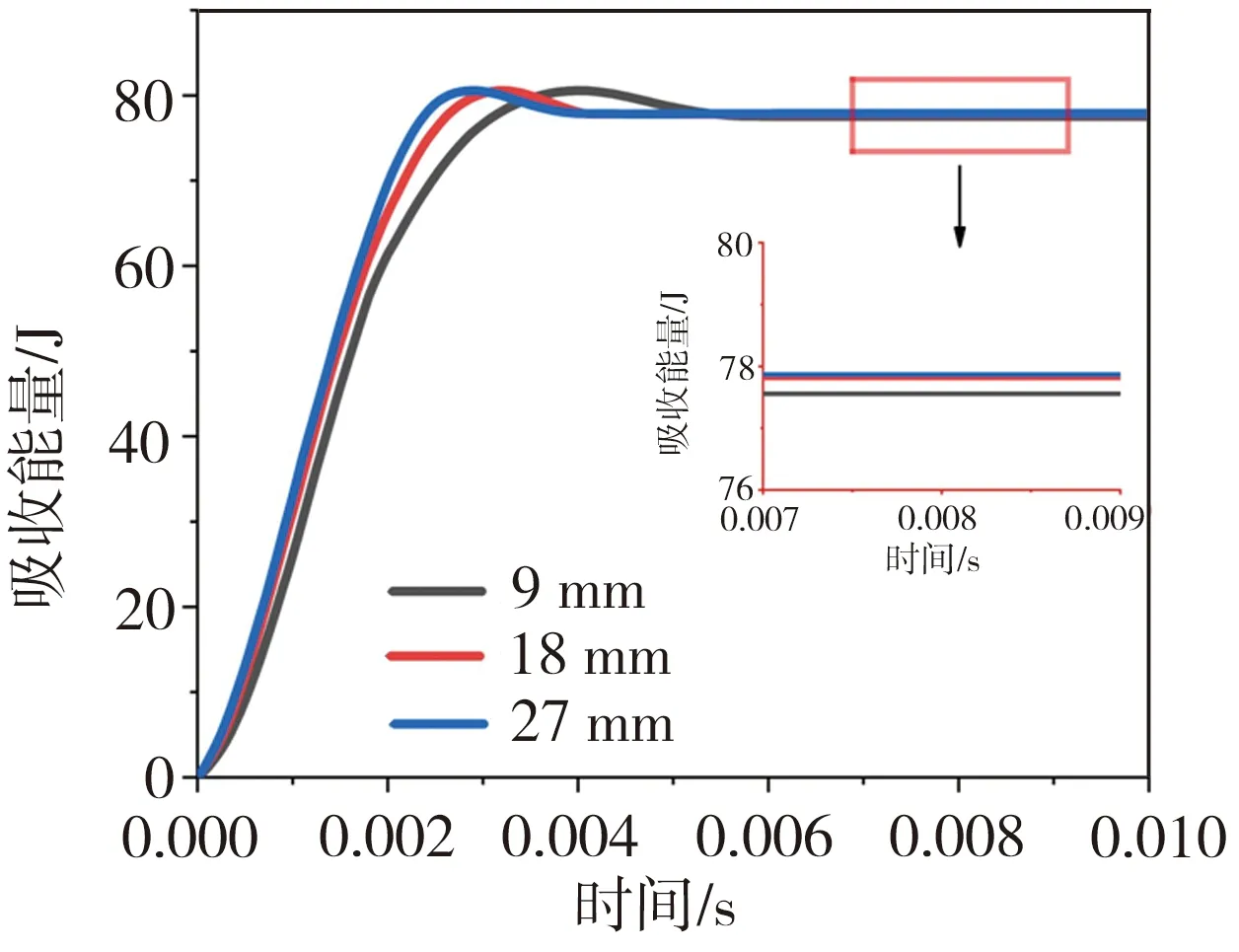
(c)蜂窝芯高度(蒙皮厚度、蜂窝芯壁厚分别为1.0、0.07 mm)

表2 吸收能量稳定值
3 结语
在冲击荷载作用下,金属材料的应变率范围包含了低、中、高三种阶段,而传统的Johnson-Cook模型不适于体现这种宽应变率条件下的金属材料本构关系,故本文以Ludwik准则和Voce准则线性组合作为新应变硬化项、CS模型作为新应变率效应项对Johnson-Cook本构模型进行改造,获得了能适用于宽应变率条件的H/V-CS本构模型。基于金属真应力-应变实验,采用全局优化算法确定了金属材料的H/V-CS本构模型参数并对模型的正确性进行了验证,所得模型参数不依赖于初值,是全局最优组合,具有准确性高、方便易得和应用便捷的优点,且不受参数数量限制。此外,还利用所建H/V-CS本构模型并结合有限元分析研究了蜂窝板结构参数对其吸能效果的影响。结果表明,改变蜂窝板的蒙皮厚度、芯层厚度和高度均会在不同程度上影响蜂窝板结构的吸能效果,蜂窝板吸收能量稳定值随蒙皮或芯层厚度的增加而增大,并随芯层高度的增加而减小,因此在实际工程中进行多方案比较和优化分析时应综合考虑材料使用功能及多种结构参数的影响。
