基于一种碰撞检测算法的液压机械臂柔顺性分析
2021-07-08刘纯键高红星
刘纯键,高红星,蒋 林,3,周 玲,赵 慧,3
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2. 武汉船用电力推进装置研究所,湖北 武汉,430064;3.武汉科技大学机器人与智能系统研究院,湖北 武汉,430081)
随着液压技术的发展,液压机械臂类机器人在工业生产中的应用日趋广泛,但仍存在人机物理接触安全性较差、在意外碰撞瞬间不能及时对碰撞进行处理等缺陷,而人机物理接触安全是该类机器人能被进一步推广应用的必要条件[1-3],因此,设计研发具有一定柔顺性的液压机械臂类机器人已成为相关领域当下的热点课题。
目前,机器人柔顺性研究主要集中在柔顺控制方面,而柔顺控制又分为主动柔顺控制和被动柔顺控制,其中被动柔顺控制是借助弹性元件或智能材料,使机器人在与外部环境接触时产生自然的顺从[4]。黄婷[5]提出了一种基于被动柔顺装置的机器人抛磨系统力/位混合控制策略,用于实现对工具末端力控制和位置控制的解耦。Mason[6]定义了空间机械臂末端力与位置的函数关系,通过建立机械臂在不同刚度条件下应对约束的相应矩阵来体现机械臂的柔顺性。蔡世波等[7]认为变刚度是实现机器人关节柔顺性控制的关键,即关节的刚度特性决定了机器人的柔顺性。然而,常用的以既定的力或位置控制精度来体现机器人柔顺控制策略好坏的方法无法评价机器人本身的柔顺性,对于变刚度机器人,虽能根据其刚度值来评价其柔顺性,但由于变刚度本身具有时变非线性,导致相关的数学模型建模困难且不够准确。针对此状况,Takakura等[8]最先基于机械臂类机器人的总能量及广义动量等物理量,提出一种无需外部传感器的有效碰撞检测方法,并为机器人在碰撞后的安全反应提供了方向信息。吴海彬等[9]对观测器的实时性与准确性进行了优化,通过构造优化函数减少观测器的延迟和振荡,并将一个与机械臂惯性相关的参数作为补偿以解决机械臂从静止到开始运动这一瞬间因惯性作用引起的观测器误检问题。康永利[10]提出了一种考虑末端负载因素的机器人碰撞检测算法,通过对末端负载部分进行辨识,使所得观测值仅体现外部碰撞力影响,有效提高了该值的准确程度。Lee等[11]提出了一种无需任何额外传感器仅依靠机械臂编码器就可对碰撞进行检测的方法,该方法利用广义动量观测器和机械臂位置控制谐波驱动中的摩擦力矩模型来估计碰撞产生的外力矩。针对碰撞检测中可能导致检测结果不稳定甚至不正确的非线性干扰因素,Zhang等[12]基于LuGre摩擦模型构建了机械手关节扰动模型,并依据广义动量理论设计了外力矩观测器,提出一种将摩擦力作为机械手运动扰动项的碰撞检测研究策略。有鉴于此,本文从机器人柔顺性本源出发,首先基于柔顺机构构型理论构建一种变刚度液压机械臂并对该机械臂进行运动学及动力学建模。之后,提出一种获取液压机械臂类机器人碰撞力的碰撞检测算法并设计该算法所需的动量偏差观测器,根据外力矩观测值来评价机械臂化解碰撞伤害的能力,此外,还利用Matlab/Simulink/SimMechanics搭建碰撞仿真平台,验证所提碰撞检测算法是否适用于液压机械臂类机器人的柔顺性分析,为研究机械臂柔顺性在意外碰撞瞬间的作用提供可行性方法。最后,基于多元非线性回归模型,对关节柔顺度、碰撞力及外力矩观测值之间的函数关系进行拟合,以期为提高机械臂在意外碰撞发生时的人机物理接触安全性提供参考。
1 液压机械臂动力学分析
1.1 机械臂几何建模
根据具体工况和变刚度液压机械臂柔顺构型理论,构建一种由液压柔顺摆动关节、液压柔顺回转关节、变刚度液压被动随动回转关节及连接件组成的5自由度变刚度液压机械臂,其整体结构如图1所示,图中θi(i=1,2,…,5)表示相应关节的角位移。该结构中的变刚度液压被动随动回转关节由液压被动柔顺关节的阀芯与第一级液压柔顺回转关节的阀体输出轴串联组成,液压被动柔顺关节结构如图2所示。该关节主要由左端的液压转角自伺服摆动缸和右端的力矩传递机构组成,当负载盘所承受外力传递到支撑轮并超过托盘所允许的安全值时,支撑轮将从托盘卡槽脱离,关节即转换为低刚度模式,通过串联部分使得第一级液压柔顺回转关节的输出减小,从而起到降低碰撞伤害程度的作用[13]。需要说明的是,变刚度液压机械臂是一种主、被动柔顺性有机结合的构件,但本研究不涉及主动柔顺控制,文中所提柔顺性均为被动柔顺性。
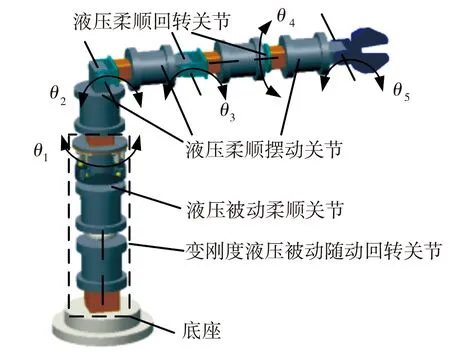
图1 机械臂结构
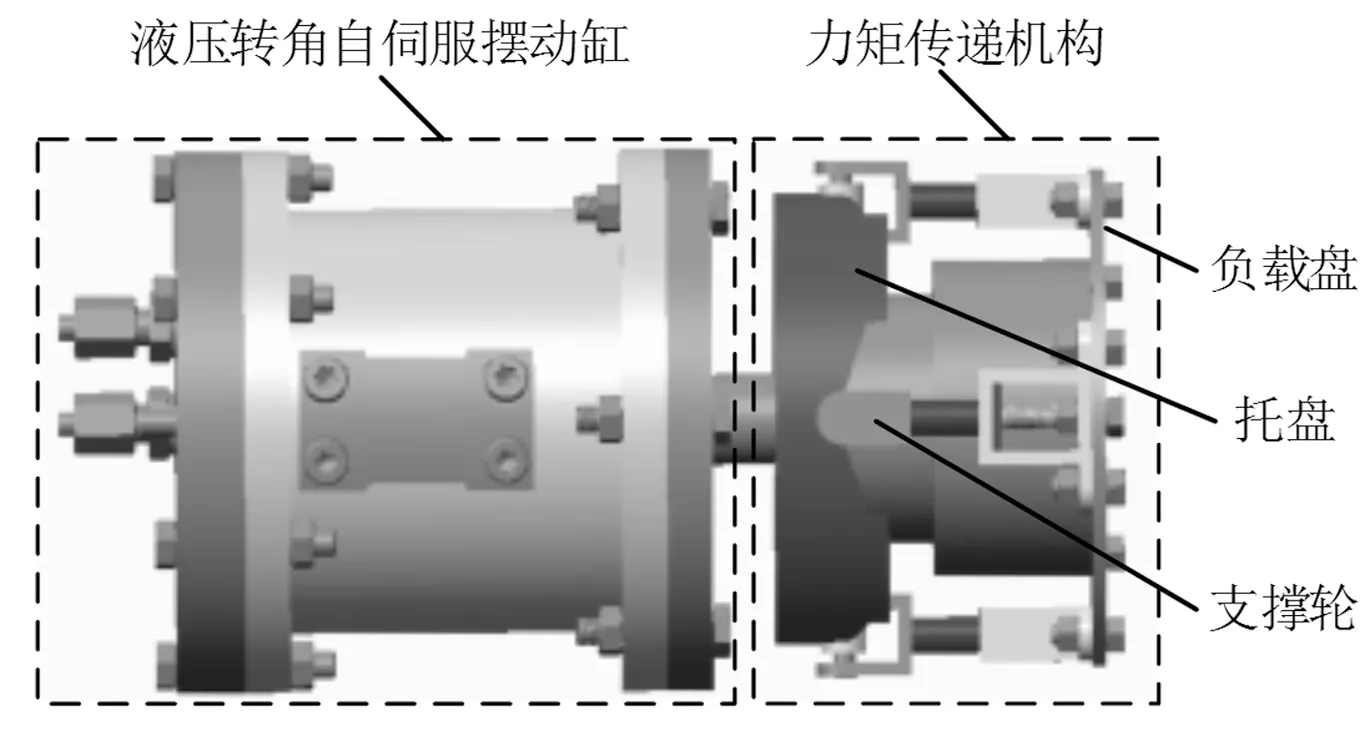
图2 液压被动柔顺关节示意图
为了更加方便地描述机械臂各关节实时的位姿状态,应用改进的D-H参数法和右手法则建立机械臂连杆坐标系如图3所示,改进的D-H参数法与经典D-H参数法的不同之处在于前者关节坐标系编号与关节编号相同,图3中以机械臂底座处为起始坐标系x0y0z0,a与d分别表示连杆长度及偏距,具体机械臂关节参数见表1,其中α表示连杆转角。根据D-H坐标参数表,使用link函数并设定5个关节的初始角度均为0,通过Matlab Robotics Toolbox平台搭建机械臂初始位置模型如图4所示。

图3 连杆坐标系

表1 机械臂D-H参数
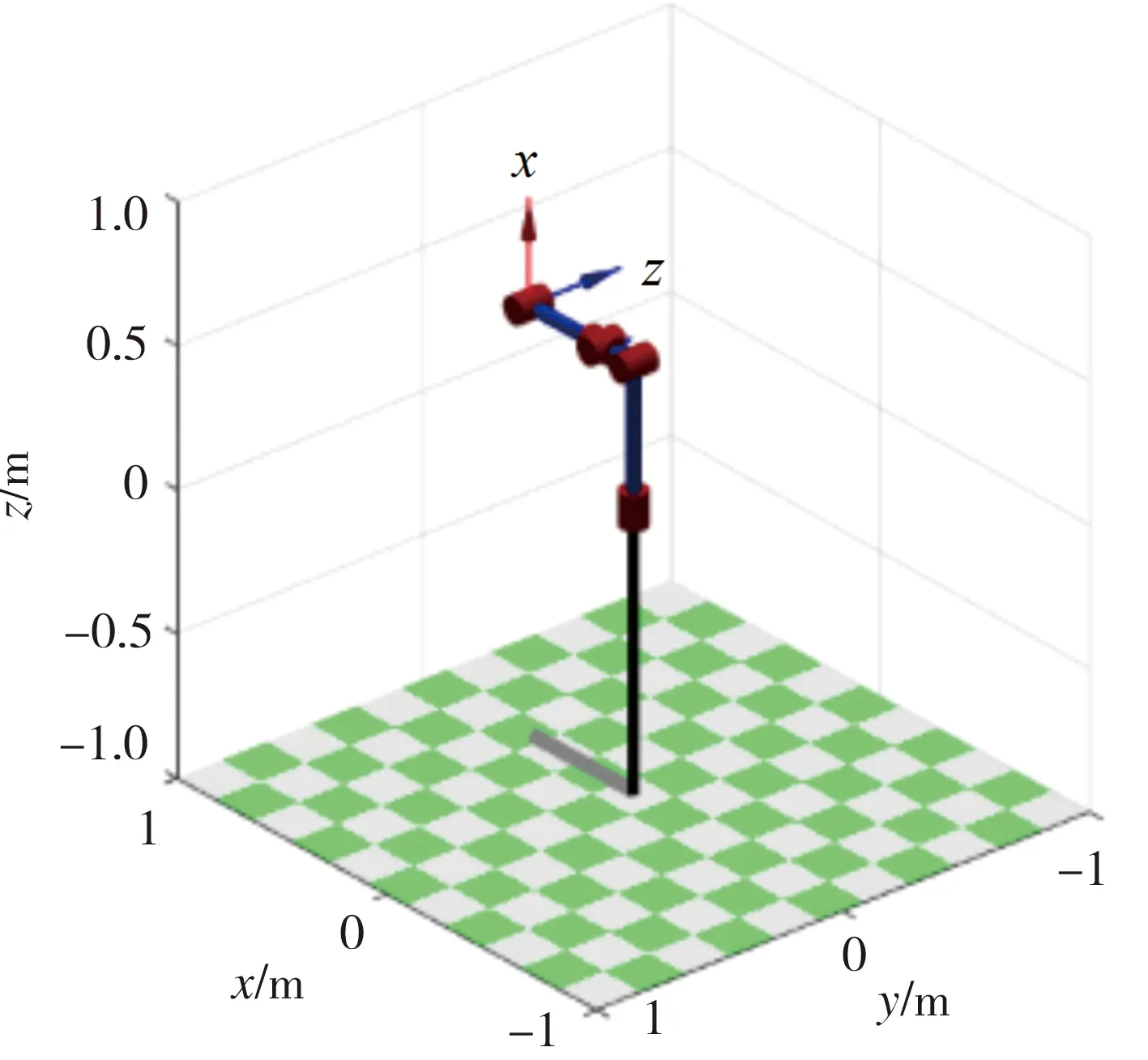
图4 机械臂初始位置
1.2 机械臂运动学规划
欲使机械臂末端到达指定位置,需所有关节协同转动,在关节转角范围内随意给定1~5号关节的转角依次为π/4、 π/5 、π/2、 -π/4、 π/6 rad,假设该点为目标工作点,采用jtraj函数对机械臂进行运动学仿真,设置仿真时长为10 s,所得仿真结果如图5所示。其中,图5(a)为机械臂末端到达目标位置时的各关节及连杆的位姿状态,同时,还对机械臂末端从初始位置到达目标位置的运动轨迹进行了模拟;图5(b)为机械臂运动过程中各关节的角位移变化曲线,从图中可见,机械臂在指定初始位置和目标位置的前提下进行点到点的运动时,各关节角位移变化曲线较平滑,无明显突变现象,且轨迹曲线末端趋于平缓,表明该机械臂不会产生振动及刚性冲击,其模型正确性得到验证。
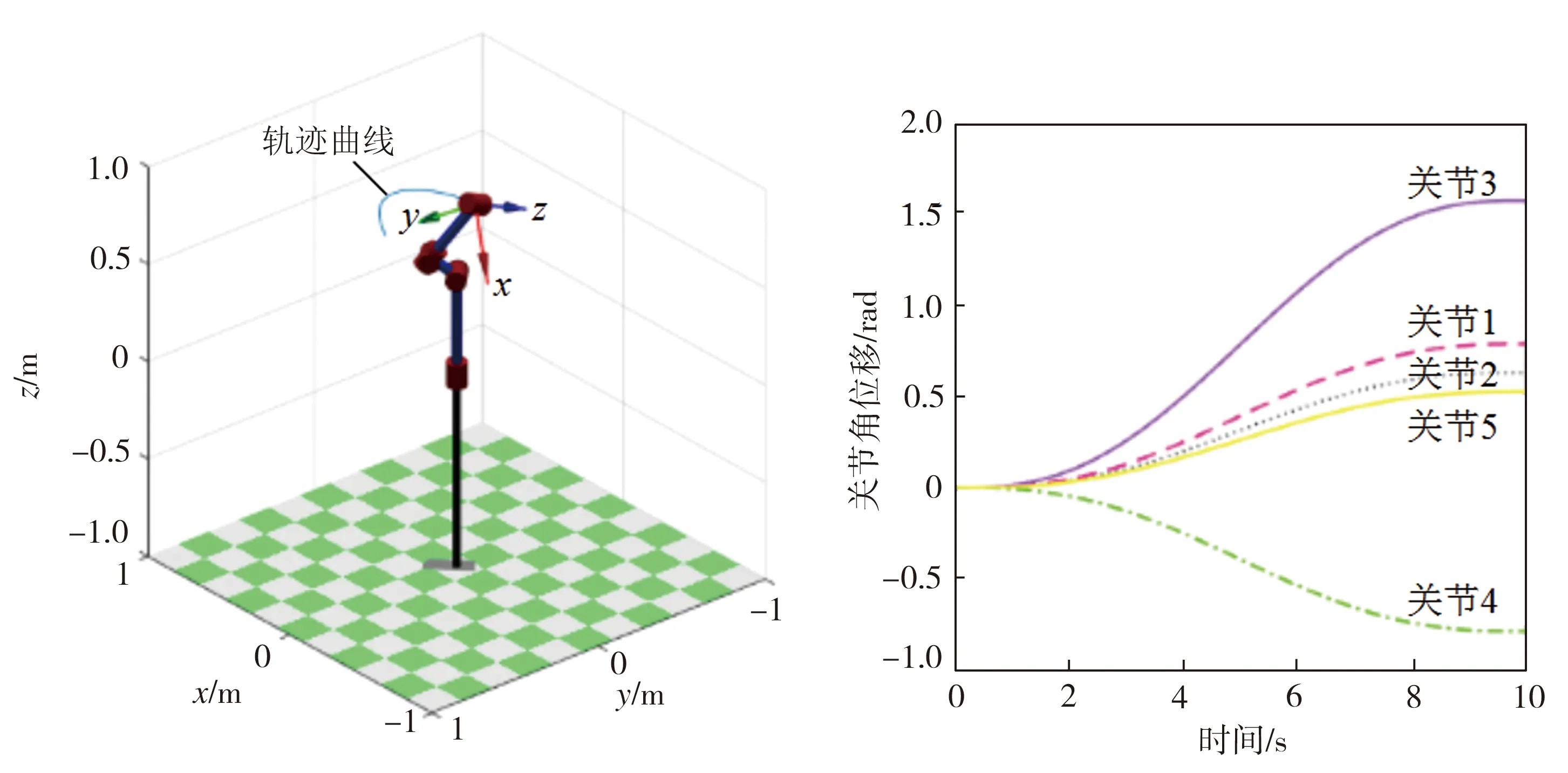
(a)机械臂末端位置仿真 (b)关节角位移变化曲线
1.3 机械臂动力学模型
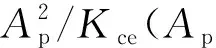
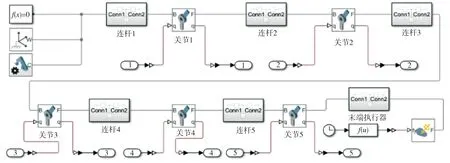
图6 机械臂的SimMechanics模型
建立机械臂动力学模型的过程包括利用已知机械臂关节位置求相应关节力矩以及利用已知关节力矩求解机械臂所产生的运动。根据液压机械臂工作原理可知,机械臂各关节均基于液压位置伺服独立控制[16]且各关节位置已知,故本研究将机械臂SimMechanics动力学模型的关节输出转角作为液压关节动力学模型的伺服输入,藉由液压关节动力学模型直接求解机械臂动力学关节力矩,其中机械臂的变刚度液压被动随动回转关节动力学模型参照文献[4],其它关节则去除具有被动柔顺性的力矩传递机构并调整部分参数。
2 动量偏差观测器的建立
在无外部传感器的机械臂碰撞检测算法中,可利用动量偏差观测器来获取机械臂的外力矩,通过比较外力矩与预设阈值的大小来判断机械臂是否发生碰撞[17]。本文在已知发生碰撞的前提下研究机械臂的柔顺性,不仅能够根据动量偏差观测器的观测结果判断机械臂是否发生了碰撞,而且还能借助机械臂刚性与柔性碰撞实验的对比更容易地评估机械臂的柔顺性。
当变刚度液压机械臂与周围环境中的人或物发生碰撞时,外部的碰撞干扰力和力矩作用在碰撞点上,对机械臂的各个关节均产生力矩作用,此时,机械臂动力学平衡方程可以表示为:
(1)
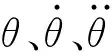
目前,大多数基于广义动量的偏差观测器都是根据式(1)所建,机械臂在发生意外碰撞时其动量通常会出现较大波动,而动量与外力矩之间又存在解耦性,因此可以根据动量偏差来设计外力矩观测器,初步定义动量偏差观测器的表达式为:
(2)
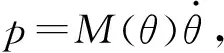
(3)
将式(3)带入式(2),得到动量偏差观测器的具体表达式为:
(4)
通过对式(4)进行分析,发现该观测器为二阶系统,然而对于典型的二阶系统,可能会因为振荡而出现较大的超调量和稳态误差,因此需为观测器添加调整函数来充当系统前馈环节以优化系统性能,调整函数fe的具体表达式为:
(5)
系统性能优化后的动量偏差观测器表达式为:
(6)
式中,z(t)为系统优化后的外力矩观测值;K4是一个正的调整矩阵,K3是一个正增益矩阵,K5为判断机械臂瞬态的参数;Gm是与机械臂末端负载及惯性相关的参数,用于提高观测值精度。根据式(6)在Simulink环境中建立动量偏差观测器的系统模型如图7所示。对于该动量偏差观测器,需要设定一个大于0的碰撞力阈值rth,当z(t)大于阈值rth时,即可认为机械臂发生了碰撞,且观测值越大,碰撞产生的冲击和造成的危害也就越大。
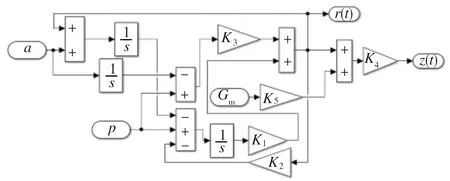
图7 动量偏差观测器Simulink系统
3 碰撞仿真实验
3.1 机械臂碰撞仿真系统
利用Matlab/Simulink/SimMechanic平台对机械臂碰撞进行仿真与分析以验证本研究所设计的变刚度液压机械臂是否具有良好的柔顺性以及能否有效减少碰撞冲击伤害,所建机械臂碰撞仿真系统主要由轨迹规划函数模型、机械臂各关节液压系统动力学模型、机械臂SimMechanic模型、负载补偿模型以及动量偏差观测器组成。该系统的具体仿真过程如下:
(1)给定机械臂的目标位置,通过轨迹规划函数模块得到机械臂各关节变量,包括关节的角度变化、关节角速度和关节角加速度。
(2)将轨迹规划获得的关节变量作为机械臂SimMechanic模型的输入,设置机械臂模型内部力学中的弹簧刚度和阻尼系数参数,利用二者等效替代液压关节的液压力,给模型添加碰撞力后得到机械臂各关节角位移变化曲线。
(3)将机械臂各关节角位移变化曲线作为各液压关节动力学模型的输入,得到液压关节角位移变化、关节角速度和输出力矩,将数据输入机械臂动力学模型以及负载补偿模型中进行计算,得到动量偏差观测器所需的计算参数。
(4)最后经由动量偏差观测器计算后输出机械臂各关节外力矩z(t)仿真结果。
3.2 机械臂碰撞力观测值分析
基于机械臂碰撞仿真系统进行机械臂的刚性与柔性碰撞对比实验。设置仿真时长为10 s,在机械臂末端位置添加一个沿y方向大小为50 N的碰撞力,通过控制变刚度液压被动随动回转关节动力学模型中的柔顺开关即力矩传递机构来切换机械臂的刚性与柔性。在仿真模拟过程中,机械臂发生刚性碰撞及柔性碰撞时外力矩的观测结果如图8所示。从图8(a)中可以看出,机械臂在发生刚性碰撞时,由于没有力矩传递机构对碰撞力进行化解,各关节仅靠自身液压弹簧刚度特性来应对冲击,因此各关节的外力矩观测值在碰撞时均产生了较明显的突变,据此可以很容易地判定机械臂发生了碰撞,且机械臂柔顺性较小、刚度较大。由于假设碰撞发生在机械臂的末端,所以对于刚性碰撞仿真系统来说,每个关节的外力矩值都应大于阈值rth,因为关节3的外力矩观测值最小,为10.61 N·m,所以设置阈值rth小于该值即可。由图8(b)可见,在力矩传递机构开启并发挥被动柔顺作用的情况下,机械臂发生柔性碰撞时各关节外力矩同样会产生一定的突变,但是由于力矩传递机构的存在,当碰撞力超过安全值时将触发机械臂被动柔顺控制,造成碰撞力还未达到较大值时机械臂就已经退让,同时各关节外力矩观测值也迅速下降,其中关节1的外力矩观测值最大,为9.78 N·m,但该值仍小于机械臂刚性碰撞时的外力矩最小值(10.61 N·m),将阈值rth定于两值之间时,即可认为经碰撞检测算法得出的结论为机械臂未发生碰撞。虽然这种判断仍存在不确定性,但仅从外力矩观测值的差别也能看出关节柔顺性对碰撞力的化解作用,比如该变刚度液压机械臂各关节外力矩观测值在柔性碰撞下均较刚性碰撞时的相应值下降了50%以上。因此不仅能够借助所建动量偏差观测器估计变刚度液压机械臂的碰撞力,而且可以通过外力矩观测值反映出机械臂对碰撞力的化解能力。
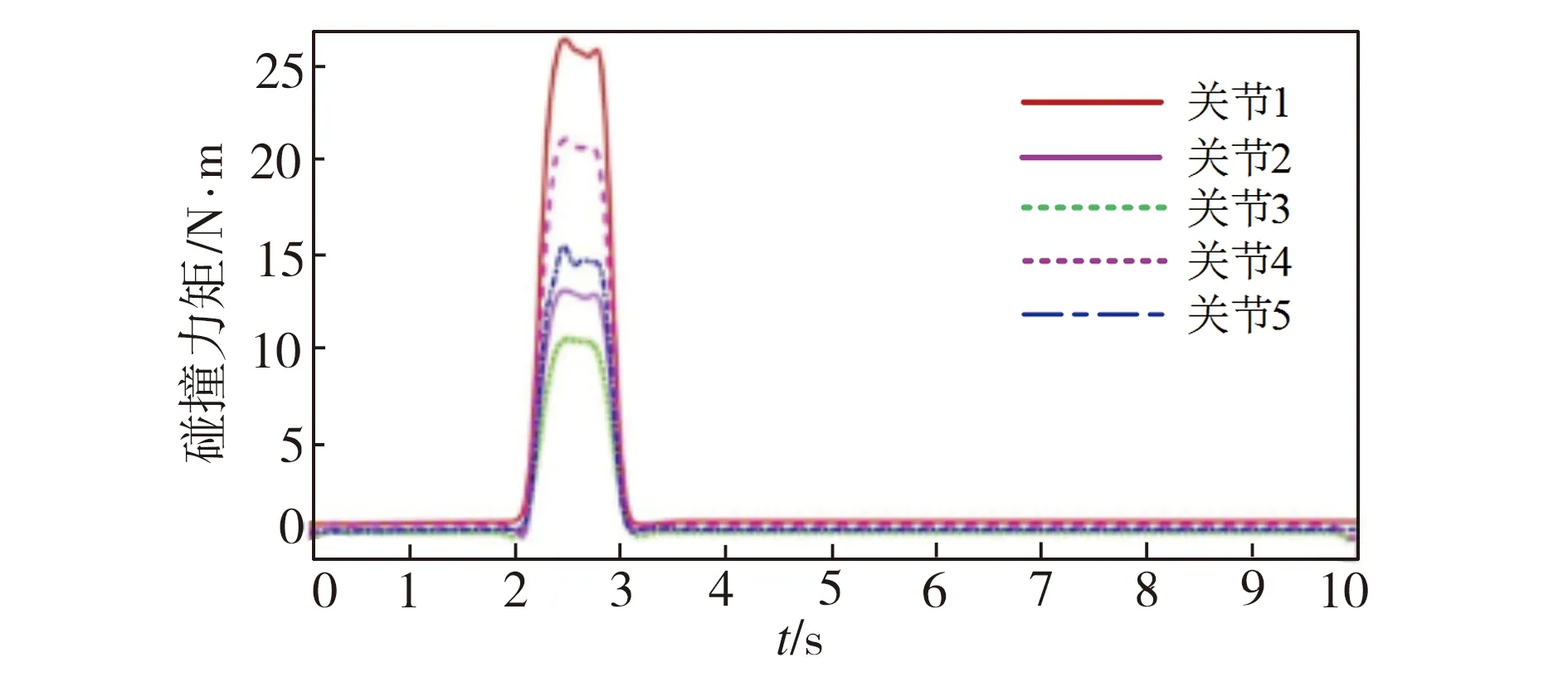
(a)刚性碰撞
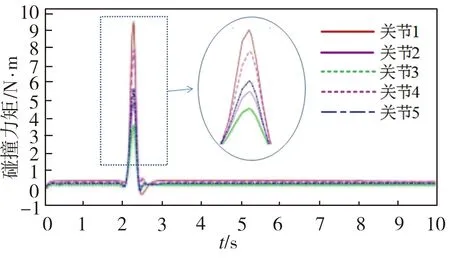
(b)柔性碰撞
3.3 机械臂柔顺性分析
借助具有特定参数和碰撞力的机械臂碰撞仿真实验虽然可获取关节外力矩值,但在缺乏连续可变化的参数化模型情况下,仅从外力矩观测值很难说明机械臂柔顺性的具体作用。为了更加清楚地明确柔顺性在意外碰撞瞬间的作用,还需构建基于柔顺度的机械臂外力矩观测值参数化模型并建立相关参数与该机械臂柔顺性之间的关系,以分析不同参数条件下机械臂柔顺性对碰撞力的化解作用。本研究设计的机械臂柔顺特性主要集中在第一级的液压被动柔顺回转关节上,其它关节的柔顺性对机械臂整体柔顺性的影响较小,因此在正常工作条件下可利用关节1的柔顺度来反映机械臂整体柔顺度。柔顺度是指关节末端受到与其输出轴满足左手规则或右手规则的力矩作用时,关节角位移偏差与力矩的比值[18],对于液压关节而言,其柔顺度R的表达式为:
(7)
式中,Δθ为关节角位移偏差,PL为液压关节负载压降,Dm为液压关节工作腔每弧度的排量,PLDm为关节力矩。该式表明,在不同的碰撞力作用下可通过调节液压关节动力学模型中的结构参数来调整关节的柔顺度。为了使机械臂具有合适的柔顺度以适应不同工作场合,有必要在一定范围内对关节柔顺度化解碰撞力的能力进行非线性回归分析,通过分析关节柔顺度在化解不同碰撞力F0时与外力矩观测值z(t)之间的关系,真正体现关节柔顺度对碰撞力的化解作用。不同柔顺度、不同碰撞力所对应的机械臂关节1外力矩观测值如表2所示。
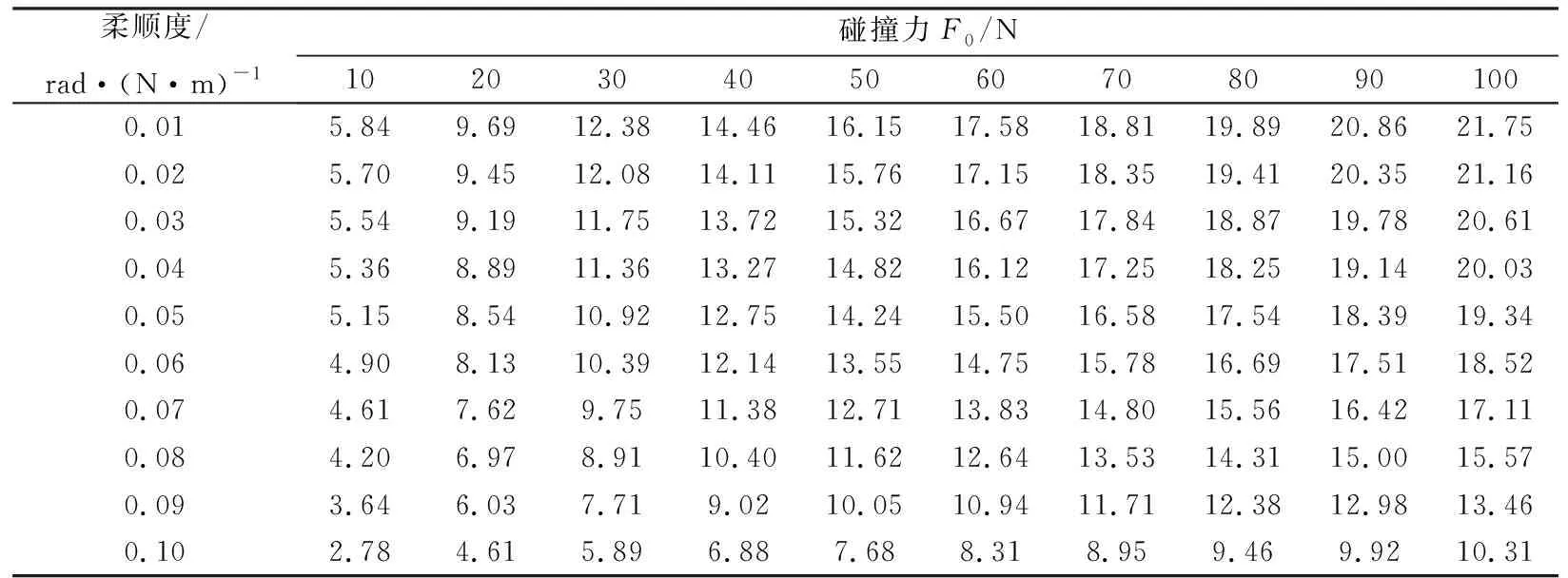
表2 外力矩观测值(单位:N·m)
在获得不同柔顺度、不同碰撞力对应的外力矩观测值散点后,需要选择合适的函数对散点进行拟合,而在未确定各参数之间的函数关系之前,通常采用多元非线性回归函数对数据进行处理。首先选用具有自定义拟合函数功能的fittype函数对数据散点进行拟合,然后再使用shading interp函数对拟合出来的曲面对象着色进行色彩的插值处理,使曲面色彩平滑过渡,最后添加colorbar通过颜色映射体现数据变化情况,得到不同柔顺度、不同碰撞力与外力矩观测值的关系如图9所示。从图9中可以看出,柔顺度、碰撞力和外力矩观测值之间存在明显的函数关系,尤其从图9(d)俯视图可以看出,关节柔顺度越大,对外部碰撞的化解能力就越强,而同一关节在化解不同的碰撞力时,其柔顺度并非简单的按比例变化。总而言之,在化解不同碰撞时,都存在一个最优的关节柔顺度值,通过外力矩观测值能揭示机械臂柔顺性的作用,选取最优柔顺度,再反过来指导机械臂的结构参数设计,这为后续研究变刚度液压机械臂的意外碰撞自化解机理提供了更全面的参考依据。
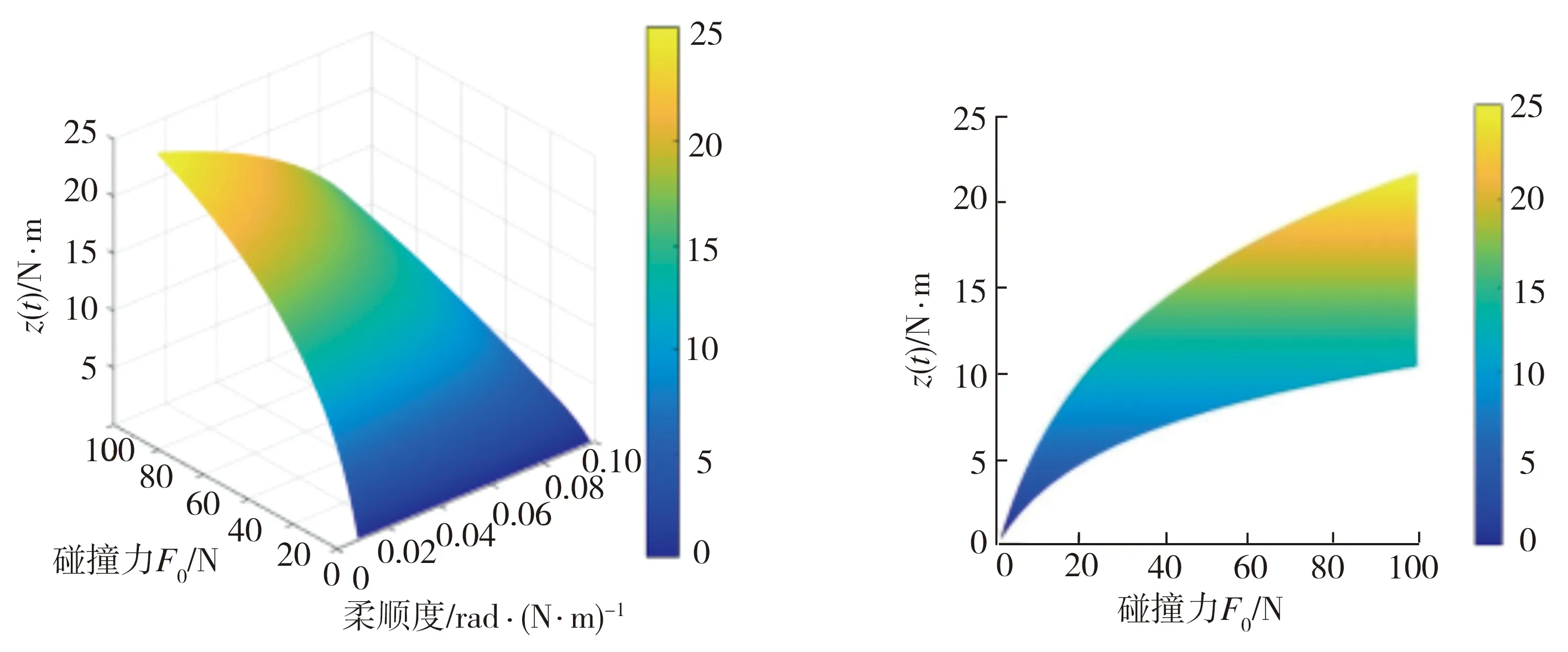
(a)三维图 (b)侧视图
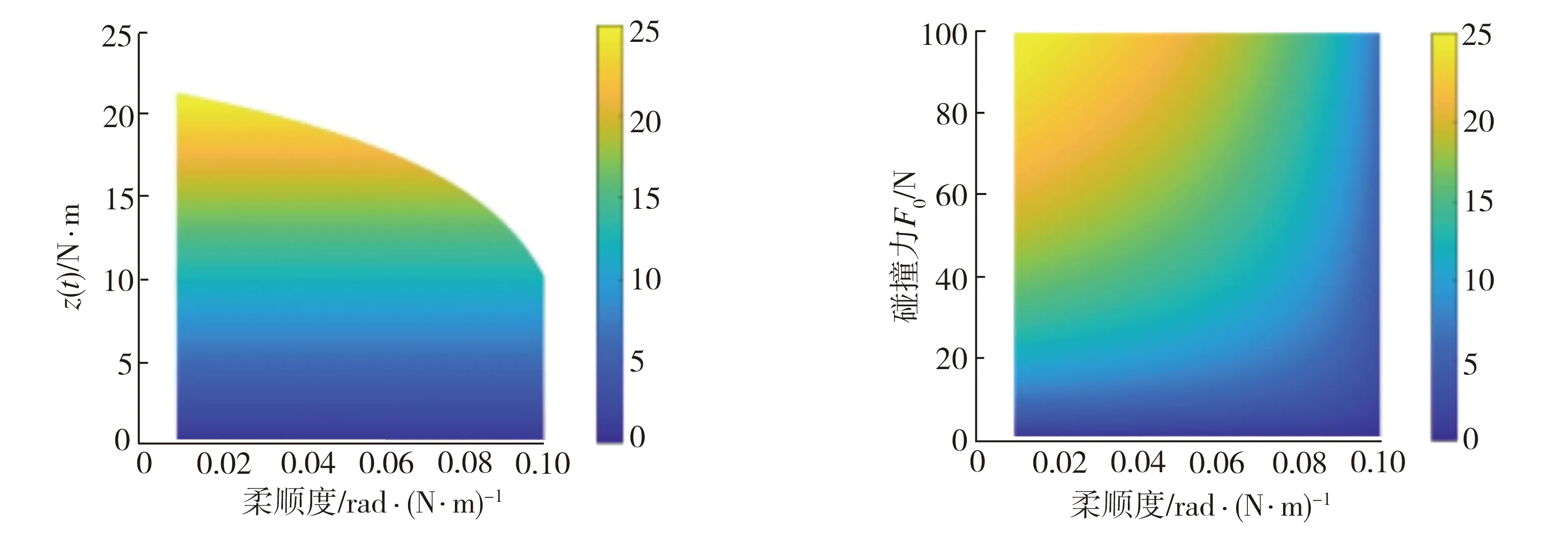
(c)主视图 (d)俯视图
综合不同柔顺度、不同碰撞力与所对应的外力矩观测值的关系,得到二元非线性回归模型为:
fitresult(λ,δ)=14.55-1.963λ+3.529δ-
0.5489λ2-0.4398λδ-0.7493δ2-0.3587λ3-
0.1319λ2δ+0.08521λδ2+0.22δ3-0.1266λ4-
0.09815λ3δ+0.05144λ2δ2-0.07115λδ3-
0.1368δ4-0.02227λ4δ+0.02912λ3δ2-
0.03869λ2δ3+0.02338λδ4+0.0631δ5
(8)
式中:λ表示柔顺度,δ表示碰撞力,fitresult(λ,δ)则表示外力矩观测值,该式的系数置信度为95%,stats返回模型的检验量如表3所示。由表3可见,所得回归方程剩余标准差仅为0.0452,能在一定程度内反映出机械臂柔顺性相关参数与其意外碰撞柔顺自化解能力之间的关系。
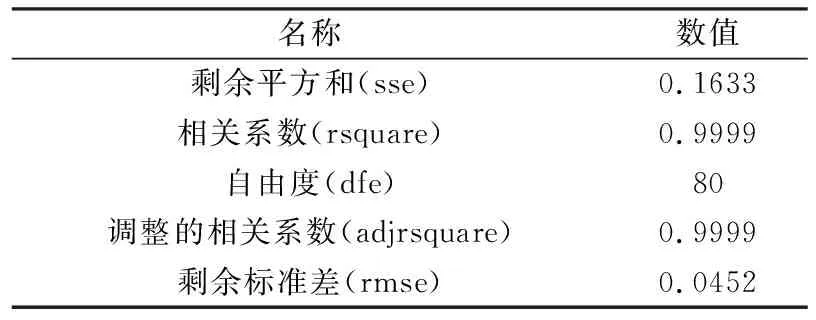
表3 二元非线性回归模型统计量
4 结语
为了提高液压机械臂类机器人的人机物理接触安全性,本文首先基于柔顺构型理论构建一种变刚度液压机械臂,该机械臂能够在受到碰撞时进行刚度切换以减小碰撞冲击,然后提出了基于一种碰撞检测算法来获取液压机械臂类机器人碰撞力的方法,该方法能够有效结合机械臂动力学模型以及液压关节动力学模型,通过外力矩观测值体现机械臂化解碰撞伤害的能力,并且借助搭建的碰撞仿真平台验证了所提方法的有效性,为研究机械臂柔顺性在意外碰撞瞬间的作用提供了可行性手段,最后基于多元非线性回归模型,对机械臂柔顺性、碰撞力与关节外力矩观测值之间的函数关系进行了拟合,拟合结果表明,外力矩观测值可反映机械臂柔顺度在化解碰撞时的作用。后续工作将为变刚度液压机械臂添加主动柔顺控制来增强其柔顺性,并在机械臂的硬件和物理样机上对本文所提柔顺性分析方法做进一步验证与优化。
