基于边界限制事件触发的Lurie系统鲁棒控制
2021-07-08张凌宇楼旭阳
张凌宇,楼旭阳*,叶 倩
(1.江南大学物联网工程学院,江苏 无锡 214122;2.无锡职业技术学院物联网技术学院,江苏 无锡 214121)
事件触发控制策略中由于其控制律更新的时刻由特定事件确定,从而减轻了计算机控制系统的通信负担,故事件触发控制策略的理论设计备受关注.Tabuada[1]定义了一种系统状态相关的事件,将阈值定义为状态相关的函数,在未考虑控制律的情况下仅依据系统信息随机选取阈值参数;Zhang等[2]建立了线性系统事件触发控制系统的一般框架,将事件定义为与误差超过时间相关的指数函数阈值,引入误差变量将闭环系统转换为连续系统,通过连续系统的稳定性分析方法对闭环系统的性能进行分析,得到系统状态最终有界的稳定性结论;李国梁等[3]研究了状态反馈事件触发控制问题,将闭环系统建模为脉冲系统,运用脉冲系统稳定性分析方法给出事件触发控制系统的稳定性定理.事件触发下闭环系统通常是一类包含离散动态和连续动态的混杂系统,故可将事件触发控制下的系统建模为混杂系统,以进一步分析其稳定性和鲁棒性.Meslem等[4]提出了一种基于边界限制的事件触发控制框架,利用混杂系统稳定性理论对闭环系统性能进行分析.目前,事件触发控制策略已被广泛应用于多智能体系统[5]、网络化系统[6]及Lurie系统[7-9]的控制研究.Lurie系统中一般包含线性系统和非线性系统,多数非线性系统均可描述为Lurie系统,因此学者们针对Lurie系统的控制及其稳定性分析展开了大量研究,如时滞问题[10-12]、量化问题[13]和脉冲同步问题[14]等.Zhang等[8-9]研究了Lurie系统的事件触发反馈控制,将事件选取为误差超过系统状态的函数,通过连续系统的稳定性分析给出系统的稳定性定理,并提出一类Lurie系统的周期事件触发控制框架,从控制策略的设计上避免了芝诺现象.受文献[4]的启发,本文拟将Lurie系统的事件触发控制闭环系统建模为混杂系统,提出一种基于边界限制事件触发的鲁棒性控制策略.

1 问题描述
1.1 连续控制
考虑如下受控Lurie系统:
(1)
式中xp=(xp1,xp2,…,xpn)T为状态变量;u∈Rm为待设计的控制输入;A∈Rn×n,B1∈Rn×q,B2∈Rn×m,C∈Rn×q为常数矩阵;对任意s1,s2∈Rq,函数f(s):Rq→Rq满足Lipschitz连续,即
|f(s1)-f(s2)|≤L|s1-s2|,
(2)
式中L>0为具有合适维度的常数矩阵.
对于系统(1),设计连续状态反馈控制器
u=-Kxp,
(3)
式中K为控制增益矩阵.
1.2 事件触发控制
基于系统(1)引入快系统xf和慢系统xs作为辅助系统[4]:
(4)
式中βf,βs为辅助系统参数,βf>1,0<βs<1. 进而利用2个辅助系统的Lyapunov函数设计系统(1)的事件触发控制策略.
事件触发时刻由集合Ds和Df确定,在事件触发控制下将控制输入u视为系统状态,联合辅助系统即可建立闭环混杂系统模型,其连续动力学为
(5)
离散动力学为
(6)
和
(7)
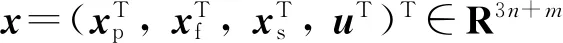
C={x∈R3n+m:Vp(xf)≤Vp(xp)≤Vp(xs)},
(8)
式中Vp(·)表示系统的Lyapunov函数.
定义如下流映射F和跃映射G:
(9)
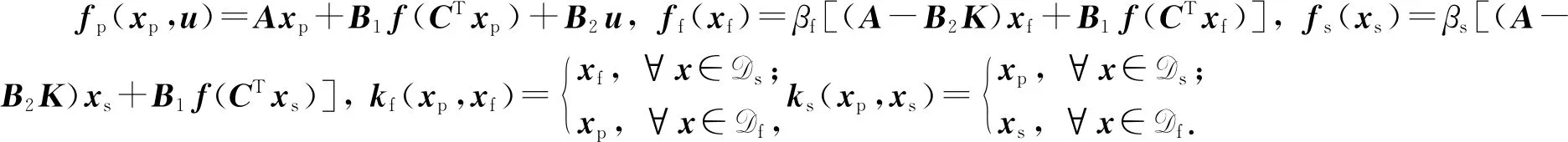
于是,可将系统(5)~(7)简化描述为如下混杂系统H形式:
(10)
2 连续控制器设计
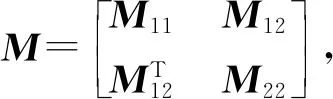
命题1若存在矩阵S和对称正定矩阵R,满足如下线性矩阵不等式:
(11)
其中反馈增益K=SR-1,则Lurie系统(1)在控制器(3)的作用下是全局渐近稳定的.
证明 考虑Lyapunov函数
(12)
其中对称正定矩阵P>0.
沿式(1)对Vp(xp)求导可得
由函数f(·)满足式(2),可得
(13)
其中
(14)
当Q<0时,系统(1)在连续控制器(3)作用下是全局渐近稳定的. 令P=R-1,K=SP,进行变量代换,式(14)等式右侧前后同乘P-1等价于
(15)
进一步地,由引理1可知式(15)等价于式(11). 证毕.
3 事件触发控制器设计
假设闭环系统(1)满足命题1,则对所有的xp∈Rn,满足
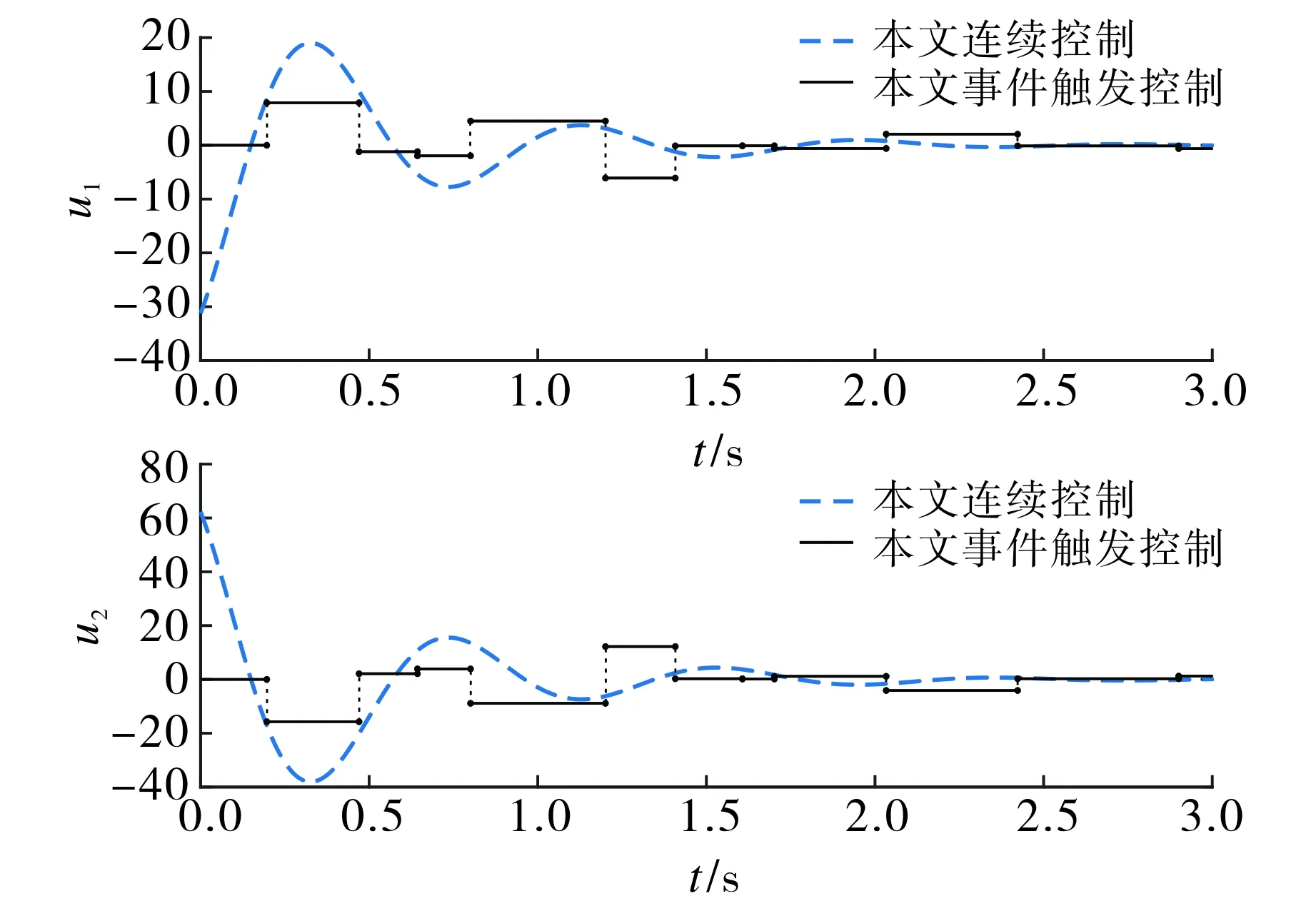
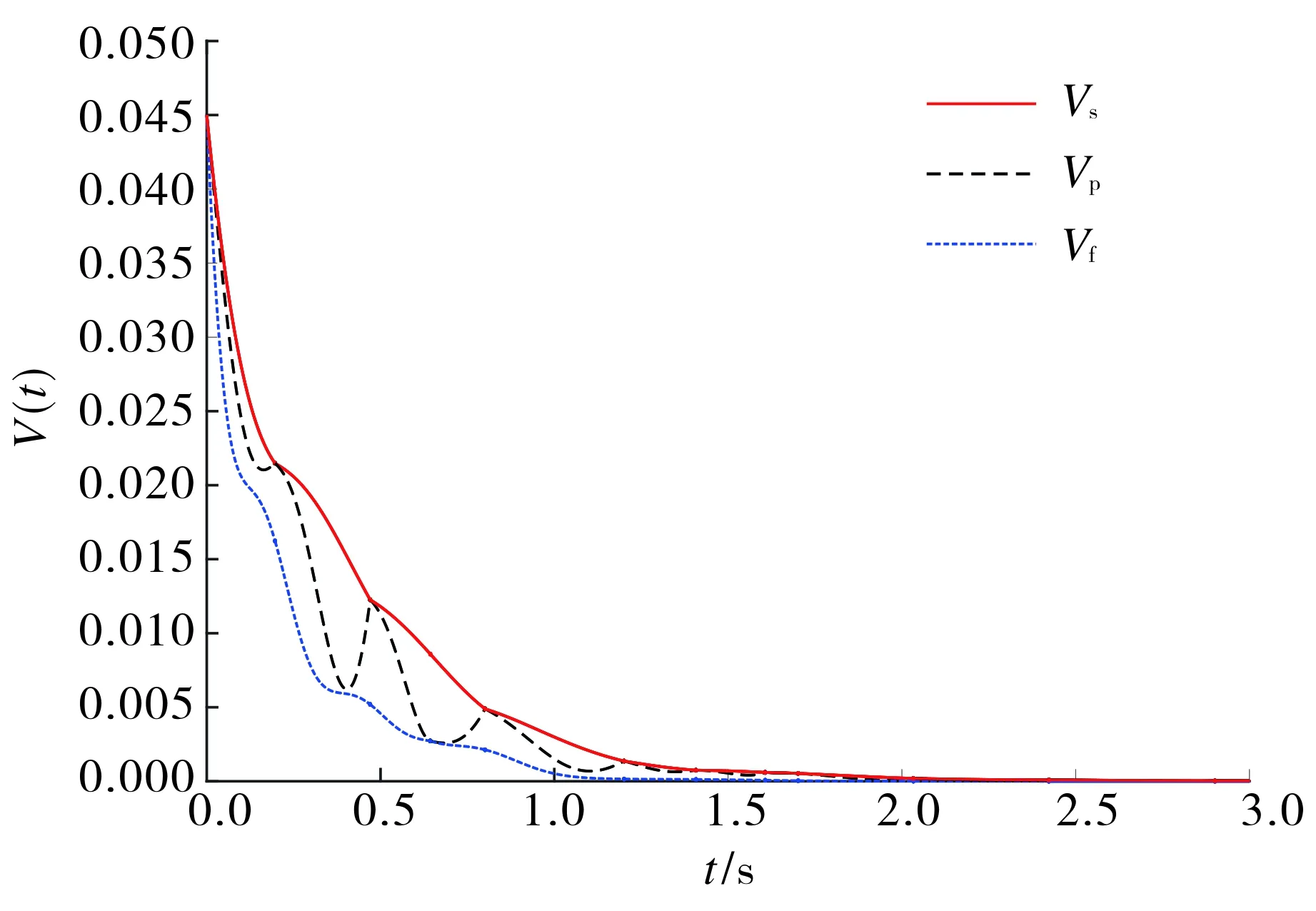
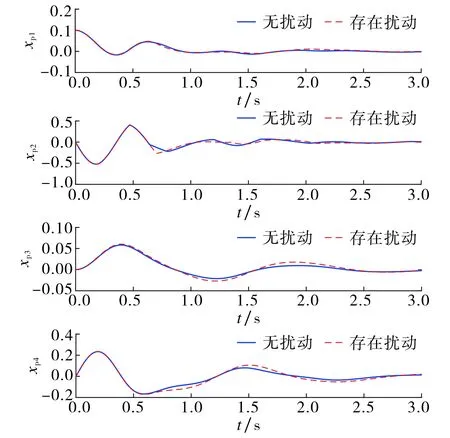
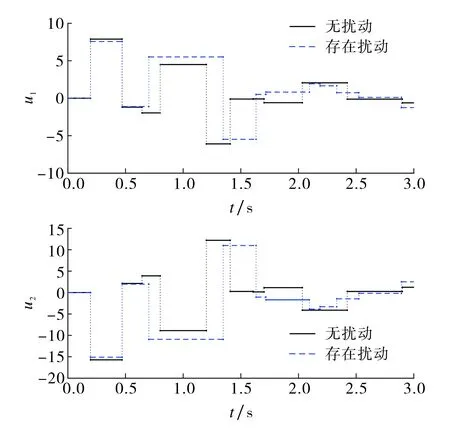
λmin(P)‖xp‖2 (16) 由快系统及慢系统的定义可知,对所有的xf∈Rn,xs∈Rn,满足 λmin(P)‖xf‖2 下面对事件触发控制下闭环系统(10)进行稳定性分析. 引理2[16]假设混杂系统H=(C,F,D,G),闭集A⊂Rn.V为系统H的一个Lyapunov函数,若存在标量α1,α2∈K∞和一个连续函数ρ∈P使得 (17) 则A对于系统H是全局渐近稳定的. 定理1假设命题1成立,则对于由式(10)定义的混杂系统H,集合 A=Ap×Af×As×Rm={0}×{0}×{0}×Rm (18) 在状态空间域C∪D上是渐近稳定的. 证明 考虑Lyapunov函数 (19) 由式(8)定义的流集可知,对任意x∈C,有 相似地,有 由此可得 |x|A=|xp|Ap+|xf|Af+|xs|As≤μ|xs|As, μ-1|x|A≤|xs|As≤|x|A. (20) 由式(12)可知,对所有x∈C,有 (21) 记 则根据式(21)可得 α1(|x|A)≤V(x)≤α2(|x|A),∀x∈C∪D∪G(D). (22) 据式(4)和式(13),对所有x∈C,有 结合式(20)可得 下面讨论排除闭环控制系统的芝诺现象,并给出定理表明闭环系统的最小事件时间间隔是正的. 定理2对于任意R>0以及0 r≤|x(t,j)|A≤R,∀(t1,j1)≤(t,j)≤(t2,j2), (23) 其中t2-t1≥tmin. 证明 给定0 考虑具有状态干扰和外部扰动的闭环混杂系统 (24) (25) (26) 式中 注1与文献[8]中基于状态误差的事件触发控制策略相比,本文所提出的触发事件设置更灵活,触发频率和控制性能均可通过辅助系统的参数来调整,并且由于所提出的事件触发控制器与被控系统是在混杂系统框架下建立的闭环系统模型,故更利于研究和分析同时具有内部状态扰动和外部干扰的系统渐近稳定的鲁棒性. 考虑一个柔性连杆系统[18],其动力学模型可由式(1)描述,参数选取如下: 定义非线性函数f(x)=sin(x),该函数满足Lipschitz连续条件,其中Lipschitz常数矩阵L可以取为单位矩阵. 根据命题1,利用MATLAB LMI工具箱求解矩阵不等式(11),得到一组可行解为 仿真中,选取式(4)中2个辅助系统参数βf=1.4,βs=0.6. 图1给出了不考虑扰动时的闭环系统连续控制器、文献[8]事件触发控制方法以及本文所提事件触发控制作用下的状态响应曲线. 为了对比系统状态收敛时间一致下的事件触发控制效果,设置文献[8]中的事件触发控制器参数α=0.8. 由图1可见3种控制器作用下系统状态收敛时间大致相同. 图2显示了文献[8]事件触发控制策略和本文所提事件触发控制策略分别作用下的事件触发时间间隔. 由图2可见,文献[8]方法下事件触发更频繁,共触发33次,而本文所提事件触发策略仅触发11次即可达到相同的稳定控制效果. 图2 不同控制策略下的事件触发时间间隔Fig.2 Inter-event intervals under different control strategies 图3给出了连续控制和事件触发控制下的控制输入曲线. 由图3可见控制器的更新是非固定周期的. 图4给出了Lyapunov函数Vp(xp),Vp(xf)和Vp(xs)的演化曲线.由图4可见,被控系统对应的Lyapunov函数曲线始终处于2个辅助系统的Lyapunov函数曲线之间,验证了式(8)中对流集C的设计要求. 图3 无扰动下的控制输入Fig.3 Control input without perturbations 图4 事件触发控制下的Lyapunov函数值Fig.4 Graphical illustration of Lyapunov functions under event-triggered control 为了验证系统镇定鲁棒性,仿真中系统扰动取[0,0.01]之间的随机扰动.扰动作用下被控系统状态的收敛曲线及事件触发控制输入曲线分别如图5~6所示. 由图5~6可见:系统状态存在扰动时控制输入的更新次数增多;当存在小扰动时,基于本文提出的事件触发控制策略仍可鲁棒镇定被控系统状态,验证了定理3的结论. 图5 存在扰动与无扰动时事件触发控制下的状态时间响应曲线Fig.5 Time responses of system states under event-triggered control with and without perturbations 图6 存在扰动与无扰动下的事件触发控制输入Fig.6 Event-triggered control with and without perturbations 本文针对Lurie非线性系统提出了一种新的基于边界限制事件触发的控制器设计方法.根据连续闭环系统的稳定性设计控制器增益矩阵,再引入辅助系统并以其Lyapunov函数为界,当被控系统的Lyapunov函数到达边界时更新控制量,否则控制量维持不变.将事件触发控制闭环系统建模为混杂系统进行稳定性分析,并讨论了系统存在外部干扰和内部扰动时的鲁棒性问题.通过柔性连杆系统仿真验证了所提控制策略的有效性和优越性.3.1 稳定性分析


3.2 最小事件时间间隔存在性
4 鲁棒性分析


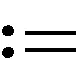

5 数值算例

6 结语
