具有河流区域的蚊虫传播动力学分析

许 瑶,凌 智

(扬州大学数学科学学院,江苏 扬州 225002)

蚊虫等媒介昆虫引起的传染病对人类造成了极大威胁．1911年英国微生物学家Ross博士通过建立一个连续的微分方程模型[1]研究疟疾在蚊虫和人群中传播的动力学行为,开启了蚊媒传染病数学模型的研究．近年来,随着“一带一路”倡议的不断推进,带来了全球化和经济的不断发展,同时也对新时期蚊媒传染病的防控造成了挑战．相对于医疗水平的提高,研究蚊媒传染病的传播机制可以从源头减少疾病的发生．数学模型的分析作为一种主要研究方法,在预测、控制甚至消除疾病等方面发挥着重要作用．例如,Cunha等[2-3]对黄热病和寨卡病毒进行相关研究;Polwiang[4-5]、丁亮[6]和王艺玮[7]等针对登革热疫情进行系列研究,而这些都是由埃及伊蚊作为媒介引发的传染病;因此,对蚊虫动力学的研究具有现实意义,可以帮助人们了解在特定环境下蚊虫的动力学行为,为相关医疗人员制定适当的控制策略提供理论依据．

本文主要研究在有开放河流的区域中蚊虫繁殖与扩散的动力学模型:

(1)

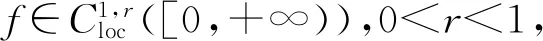
1 比较原理

为了得到解的存在唯一性,引入针对问题(1)的上下解定义．记Du,T=R×(0,T),Du,T∪ΓT=R×[0,T),Dv,T=Ω×(0,T),Dv,T∪ΓT=Ω0×[0,T),Ω={(x,y):x∈R,y>0},Ω0={(x,y):x∈R,y≥0}．

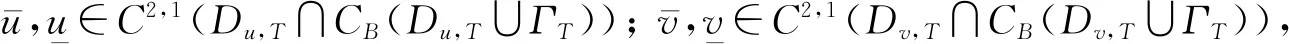
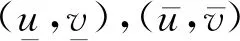
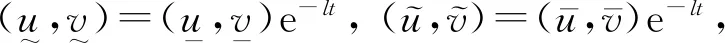
(2)

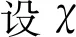
2 解的存在唯一性

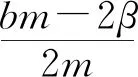
的解有界．

证明 记方程组的解为u*(x,t),有

(3)

显然,问题

(4)

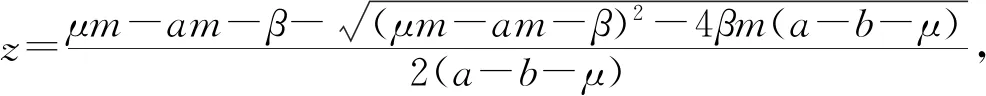
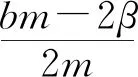
证明 分三步完成证明．

1)近似解．类似文献[9]中证明过程,有

(5)

(6)

从vn-1(n=1)>0开始,不难看出方程组(5)和(6)每一步都可解,且un,vn非负．下面重点讨论方程组(5)．

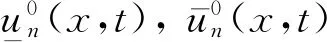
(7)

(8)

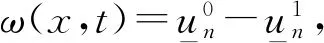
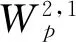
3)收敛性．在步骤(2)的基础上取p>N+1,通过Morrey不等式可以得到(un)n,(vn)n关于Cα(0<α<1)的模也是一致有界的．通过Schauder估计,它们对时间的导数和空间二阶导数在紧集上一致Hölder连续,所以(un,vn)n收敛于(u,v),得到limn→+∞(un,vn)=(u,v)．由步骤(1)可知(u,v)是非负有界的．

综上所述,解的存在唯一性得证．

3 解的长时间行为

引理5如果b>γm+a,那么方程组

(9)

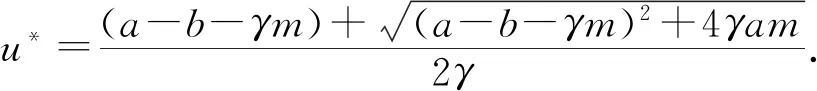
证明 该证明与文献[10]中定理4.6的证明过程类似,此处省略．

定理6设(u,v)是方程(1)的唯一解,如果b>γm+a,β/μ=u*,那么(u,v)满足limt→+∞(u(t,x),v(t,x,y))→(u*,1)．

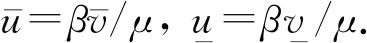
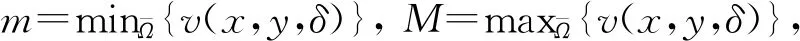
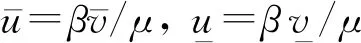
4 数值模拟分析

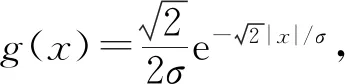
选取参数a=0.4,b=0.5,m=0.4,μ=0.5,β=0.4,γ=1/12,使其满足定理6中条件;D=10,d=100,即蚊虫在田野上的扩散速度比河流快;Lx=200,Ly=100,σ=25;步长Δx=Δy=1 m,Δt=0.001 d;考察5 000次迭代,即t≤5 d;初始条件为

其中δ=0.5．

图1和图2分别表示随着时间变化河流和田野区域中蚊虫的密度分布．不难看出,如果时间取得足够大,蚊虫的密度将趋向于稳定的数值,即limt→∞(u,v)→(β/μ,1)=(0.8,1),从而验证了定理6的结论．

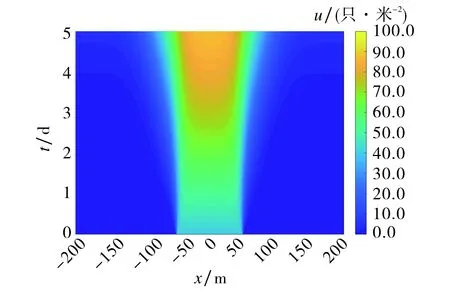
图1 预设参数值下河流蚊虫在不同时刻的密度分布Fig.1 Density distribution of mosquitoes at different time points on the river under preset parameters

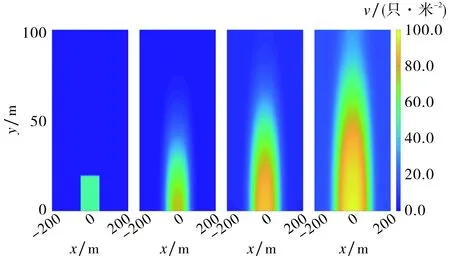
(a)t=0.0 d (b)t=2.0 d (c)t=3.5 d (d)t=5.0 d图2 预设参数值下田野蚊虫在不同时刻的密度分布Fig.2 Density distribution of mosquitoes at different time points in the field under preset parameters