末敏探测高速转台的静动态特性分析*

雷秉山，雷志勇，王泽民，李 静

(1.西安工业大学 机电工程学院，西安710021；2.西安工业大学 电子信息工程学院，西安710021)

末敏探测系统作为智能弹药工程的重要组成部分，是军事探测领域研究热点之一。末敏探测的研究主要通过高塔测试的方法实现对地面目标进行识别。为了模拟这种稳态扫描探测过程，作为装载探测系统的转台直接决定着末敏探测系统的主要探测指标上限。更高的扫描速度和装载更多元探测器的预研发展需求也需要设计出高转速下稳定性好的高速转台。因此，进行末敏系统实验转台的结构研究是配套末敏探测系统做好预研实验准备的主要基础条件之一。

近几年，转台在机载探测、舰载探测和车载探测等军用及民用领域都有广泛的应用[1]。转台作为光电探测系统的主要组成部分，直接影响着探测系统的动态精度和可靠性[2]。目前国内学者对转台的机械结构分析和拓扑优化设计开展了广泛的研究。文献[3]设计了一台应用于机载平台下的高精密单轴伺服转台，对结构的应力分布、位移分布和固有频率进行了分析，仿真结果表明转台设计符合安全性和动力学性能的要求，但该研究针对单轴转台中的负载基座进行模态分析，并未对单轴转台整体进行模型简化分析。文献[4]通过有限元仿真软件对主动防护发射转台进行了研究，通过施加载荷的方法模拟工程实际应用时，结构的负载和受力变化情况，得到结构的应力云图、变形云图和前6阶固有频率，虽然给出了求解固有频率的理论方程，但没有给出主动防护发射转台模型具体的固有频率理论计算值。文献[5]通过ADAMS仿真软件建立掘进机的结构模型，得到回转台结构的应力和应变云图，并进一步对结构进行了拓扑优化，实现了轻量化的指标要求，并更进一步对拓扑优化前后的掘进机模型的静力学进行了深层次的剖析，但没有给出拓扑优化后模型的模态分析结果。文献[6]提出函数全微分理论对用于惯导系统的转台的工作精度进行了分析，得到了转台误差灵敏度模型，找到了影响转台精度的关键误差源，文中提出的分析方法只适合目标跟踪类转台的理论分析。另外，许多学者对机械结构分析利用ANSYS Workbench等仿真软件进行结构力学分析[7-9]，但考虑了具体承载对象和应用场合等特定条件。基于这种特殊性，通过借鉴其他学者的研究经验，针对末敏探测实验转台进行理论与仿真分析，为末敏探测转台设计提供设计依据。

因此，在上述思想的基础上，考虑扫描探测所需扫描速度变化量，探测角度变化量和载荷变化量，建立末敏探测高速转台的静力学与动力学数学模型，并通过有限元分析使设计的转台能够满足高塔末敏探测实验指标要求。

1 转台系统总体结构

末敏探测的实验研究，主要通过将转台系统和探测系统架设在高塔上，从空中对地面目标进行探测。转台系统分为俯仰与回转二轴转台、转台测控系统和安装底座支架三部分组成。转台系统必须考虑便于固定安装，控制系统可以远距离监测与控制，安装基面可微调整等实际问题。保证测试人员可以安全快速的搭建好实验平台并可以离塔进行转台控制。

1.1 二轴转台结构

二轴转台的结构设计主要实现探测角度、探测转速和探测系统负载固定的功能要求，俯仰轴的俯仰范围为0°～70°，回转轴的转速为0～4 500 r·min-1。转台各轴系采用角接触轴承组成，俯仰轴上安装旋转编码器实现对旋转量的反馈调节，回转轴安装大于50信道的导电滑环。探测系统安装在方型负载内框中。二轴转台台体的结构剖视图，如图1所示。

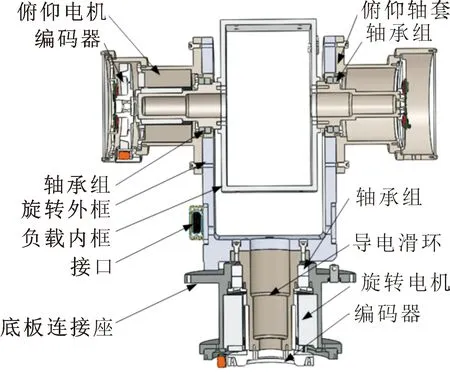
图1 二轴转台剖面图

根据指标要求，文中设计的二轴转台旋转外框为U型设计，负载内框采用O型设计，负载框体负责固定探测系统。考虑转台会绕中心轴高速旋转，其动平衡性能会影响转台的稳定性，故设计成左右对称结构，保证转台左右配重相同。转台整体框架结构是支撑转台的受力件，在满足负载能力外，框架结构刚性和转动惯量也要尽可能小，所以在框架结构材料选择上,转台总重量不能大于60 kg。为保证转台的机械稳定性，主轴零件的材料选用优质的合金钢40Cr材料，满足俯仰及回转两轴的强度和刚度要求。轴承组的选择，需要考虑负载重量，根据实验负载的变化范围，当负载重量小于3 kg时，速率范围为1°/s～21 600°/s，且负载重量等于3 kg时，最大速率为21 600°/s，此时的离心力最大，通过计算得到离心力F=mω2r=3×(21 600/180×π)2×0.005=2 131.8 N；当负载3～20 kg时，速率范围：1°/s～7 200°/s，且负载重量为20 kg时，最大速率为7 200°/s，此时的离心力最大，通过计算得到离心力F=1 579.1 N。转台方案采用上下各一对角接触球轴承支撑轴系，其额定负荷能力为9 700 kg。回转轴系及负载总的转动惯量约为I=0.28 kg·m2。根据实验要求，最大运动速率设定为21 600°/s，最大角加速度设定为1 080°/s2，力矩T为5.3 Nm。回转电机选用交流伺服电机驱动，型号为SCN164-045-016C。导电滑环总环数为50道，其中20道为信号环单芯屏蔽线，30道为电源环，滑环允许最高转速为4 000 r·min-1。

1.2 转台调平支架

根据末敏高塔现场环境情况，设计了一套转台调平支架，如图2所示，主要由调平底座、安装底座和支撑架结构组成。

图2 转台调平支架

调整底座水平使得转台安装面调整到所需的水平状态，然后用固定螺母将高速转台安装在调平底座上，调平底座固定在安装底座上，支撑架对安装底座提供支撑。

1.3 转台测控系统

转台测控系统，包含DSP控制板、电机驱动器、电气开关、电源、配套机箱和电缆等，完成实时控制计算、控制单元的管理、故障检测和外部通信等工作。电控系统为三环控制结构，即电流环、速率环和位置环，控制方案如图3所示。电流环在功率放大器内部实现，速率PID与位置PID由控制软件实现。

图3 控制系统结构

为了保证转台的控制精度，需要回转电机获得最大允许电流，从而加快动态过程。当电机过载甚至堵转时，限制电枢电流的最大值，起到快速自动保护作用。所以采用电流负反馈控制，将电机伺服控制电流取样后引入控制回路，使伺服电机能按控制规律获得最快最大的驱动电流。在电流环的基础上，再增加一个速度闭环回路用来构成局部反馈校正，由于调解器采用PI调节器，从而减少了摩擦等非线性的影响，提高了系统稳态精度。另外，速度环的存在还保证了在位置环发生故障的情况下，系统仍然能够闭环，不至于超速以出现故障。在位置环控制下，PWM功率放大器自身配有电流负反馈回路，对减小电气时间常数、拓宽系统频带、减小驱动部件的死区起重要作用。速度环起进一步拓宽系统频带、提高速率响应速度、抑制电机力矩波动和干摩擦等对系统的影响。

2 转台结构力学模型的建立

末敏探测高速转台是一套丰富而庞杂的系统。为了便于转台结构的力学特征分析，需要将结构进行适当的简化，形成一种分析静力载荷与振荡特性的理想化模型。为了研究转台的静力与振荡的机理，需要结合材料力学与动力学的理论分析方法，建立转台结构的数学模型,最终给出末敏探测高速转台的力学表达式。

2.1 高速转台的静力学模型

转台静力载荷的分析是有限元分析的重要部分之一。文中根据末敏探测高速转台上的探测系统负载等受力情况进行载荷的加载并对边界条件进行约束。末敏探测系统安装在转台的负载内框中，其静力载荷变化对起始扫描点位置的精确定位产生重要影响。因此需要建立转台的静力学的数学表达模型，为分析转台静压力变形对扫描起始点的定位精度影响提供理论依据[10]。

建立末敏探测高速转台的静力学模型时，需假设材料是均匀分布的，利用有限元分析法求解出在转台结构上划分的节点位移及节点应力。通用动力学方程为

(1)

假设转台所有物理量均不随时间而变化,可以根据式(1)得到转台线性结构静态分析的等效方程为

Mu=F,

(2)

式中：u为有限元节点位移矢量;F为转台的静力载荷。

通过对式(2)的求解，可得到各节点的位移矢量。根据位移插值函数，弹性力学分析中给出各节点的应力与应变表达式为

τet=Bu-τh,σ=Dτh,

(3)

式中：τet为由应力引起的应变；B为节点上的应变；u为节点的位移矢量；τh为热应变矢量；σ为应力矢量；D为弹性矩阵。

求解有限元表达式(3)，即可求出转台中单位节点相对应的应力值。在实际工程运用中，对于各节点的解算，是通过ANSYS软件对建立的模型进行有限元节点划分，然后对各个节点进行计算。

2.2 高速转台的动力学模型

对末敏探测高速转台的动力学模型的分析主要是对其模态进行分析建模，也就是求得高速转台结构的固有频率的表达式。因为外部载荷对高速转台的固有频率几乎没有影响，分析时不需考虑施加的外部负载。高速转台整体结构是一个多自由度系统，设转台轴线的横向自由振动为w(x,t),转台简化模型密度为ρ，x截面处的结构刚度为EI,截面面积为A，则转台模型的运动微分方程为

(4)

该偏微分方程的自由振动解为w(x,t)=W(x)T(t)，将此代入到转台的运动微分方程可得：

W(x)=C1cosβx+C2sinβx+C3coshβx+

C4sinhβx，

(5)

T(t)=Acoswt+Bsinwt，

(6)

转台模型的边界条件为

w(x=0)=0，

(7)

(8)

(9)

(10)

将边界条件式(7),式(8)代入式(5)可得到：

W(x)=C1(cosβx-coshβx)+

C2(sinβx-sinhβx)。

(11)

再将边界条件式(9)，式(10)代入式(5)中可得：

-C1(cosβl+coshβl)-C2(sinβl+sinhβl)=0。

(12)

-C1(-sinβl+sinhβl)-C2(cosβl+coshβl)=0。

(13)

要求式(12)，式(13)中C1和C2有非零解，则它们的系数行列式必为零，即:

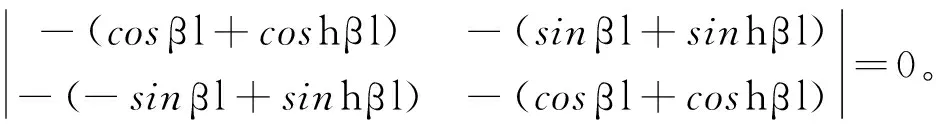
(14)

得到转台系统的频率方程为

cos(βnl)cosh(βnl)=-1。

(15)

该方程的根βnl表示转台系统的固有频率，转台系统的固有频率可表示为

(16)

通过查询机械设计手册中表格数据值[11]，可得到βnl的值，β1l=1.875 104，β2l=4.694 09，β3l=7.854 75，β4l=10.995 54，β5l=14.137 25，β6l=17.832 34。

将βnl的值代入式(16)，可得到转台模型前6阶固有频率的理论计算值。假设相对于βn的C2值表示为C2n，根据式(12)中C1n与C2n的关系可得:

(17)

最终可以得到高速转台模型的固有频率一般表达式为

Wn(x)=C1n[(cosβnx-coshβnx)-

n=1,2,…。

(18)

通过对高速转台动力学模型的建立，可以发现高速转台系统的固有频率与系统的边界条件有密切的关系。改变高速转台系统的结构和边界约束条件就能达到改变高速转台系统固有频率的目的，进而可合理的优化高速转台结构。为了验证本章节中提出的转台静与动力学理论模型的正确性，需要对高速转台进行有限元仿真分析。

3 高速转台结构的有限元分析

转台结构在静载荷作用下结构的应变与变形是静力学分析的重要步骤。考虑高速转台的结构特点，转台设计为轴对称结构并保证中心轴两侧的配重尽量一致。对转台上主要构件进行载荷的加载和边界条件约束的施加。载荷的施加主要包括：对转台框架底面施加约束，约束底面的六个自由度；对负载和转台主要构件组成的重力载荷计算；模拟回转电机工作状态下，转台高速旋转产生的惯性力矩，其中风阻和摩擦力矩造成的影响很微小，故不带入进行求解。

3.1 高速转台的有限元模型

建立高速转台的简化模型，将高速转台三维模型中不属于承载结构的外购设备包括探测负载、电机、编码器、驱动器等部件进行简化。通过查阅外购设备说明书中的重量，在仿真计算中施加相应的载荷，同时忽略螺栓和部分螺纹孔，将结构上的细节特征进行压缩处理。根据简化模型中各部件所用材料类型，在ANSYS Workbench中进行部件材料属性设置[12]参数见表1。

表1 材料属性

转台结构简化后零件数量为14件，其中大结构零件为左右俯仰轴套、俯仰框架、U型架和方位轴共5件，其余为俯仰轴承、轴承内外压圈等小结构零件共9件。确定出求解域，对其网格划分。划分时，考虑转台各零件不同材料，需要将其离散为实体单元，调节构件不同部位的网格密度，通过不同网格密度划分的对比，智能网格划分的方法解算出的结果与自定义划分相近。所以对转台采用智能网格模型的节点数为122 890，单元数为225 885，得到的转台有限元模型如图4所示，单元类型为Solid 45六面体单元。

图4 转台的有限元模型

3.2 高速转台静力学求解与结果分析

根据高速转台简化模型，对其进行边界条件的约束。负载内框架通过螺栓与俯仰轴相连接，外框架与回转轴承安装在一起。所以对回转轴上的轴承进行约束，对回转轴上的轴承的三个方向进行约束，限制它的运动。同时根据转台的载荷进行设置，增加重力载荷、探测系统载荷和惯性力矩载荷来对转台静力学进行分析。图5为高速转台简化模型在静力载荷作用下的位移形变图。从图5可看出，高速转台简化模型的最大变形出现在转台内框架底端平面，最大位移量为2.227 75×10-2mm，转台外框架部分位移小，转台左右两侧轴套结构形变量为1.265 3×10-2mm满足高速旋转下的结构载荷要求。但实际工程运用中，必须根据探测负载的载荷指标要求结合静力学仿真参数结果，通过添加加强筋对内负载框进行刚度强化。

图5 高速转台简化模型的位移变化云图

图6为高速转台简化模型在静力作用下的等效应力云图。

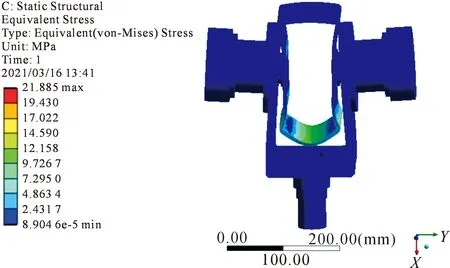
图6 高速转台简化模型的应力变化云图

从图6可看出，高速转台简化模型的最大应力为δmax=12.158×106Pa，最大应力区域出现在俯仰轴与内负载框连接处和内负载框底端面处。轴系的材料为40Cr材料的剪切许用应力为δmax=21.11×107Pa，其结合实际的工况，取一定的安全系数3，有δ<δmax/3=7.036×107Pa，可以得出在静载荷作用条件下对结构整体应力影响不大，结构强度满足设计要求。

3.3 高速转台动力学求解与结果分析

为了避免转台在带负载情况下，其固有频率与外界输入的激励频率一致，导致转台发生振荡。从而导致光电探测系统扫描轨迹线的跳跃变化，影响对地面装甲目标的轮廓解算。对高速转台简化模型进行模态分析，在通用动力学方程的基础上，假定结构材料为弹性材料，整体刚性不变和整体质量不变。同时，默认材料为线性分析求解，不考虑材料的非线性特性。

理论上，高速转台有无限多个固有频率，且固有频率值会随着阶数的增加而逐渐变大。在转台实际工程运用中，高阶模态振荡能量占比很低，对结构振频的影响不大，考虑转台自激振荡的频率不高，因此只分析转台较低阶模态的固有频率。本文通过在有限元模块中建立好的简化模型作为模态分析对象，不对转台模型施加结构载荷，设定转台的频率范围为0～10 000 Hz，使用Block Lanczos模块对转台进行提取[13]。图7为转台前6阶振型图，可以看出转台简化模型前6阶固有频率范围为121.63～805.83 Hz。高速转台系统的外部激励来源于回转电机运行时的振动，回转电机的额定转速为3 000 r·min-1，最高转速为5 000 r·min-1。电机转速与频率的关系方程为

n=60f，

(19)

式中：n为电机转速；f为电机振动频率。

根据式(19)求得回转电机按照最高转速5 000 r·min-1时的自激振频为83.3 Hz。而转台整体结构的一阶振动频率为121.63 Hz，比回转电机带来的外部激励的频率要大38.33 Hz,设计满足指标要求，不会发生共振。

通过高速转台前6阶固有频率有限元仿真结果与文中动力学数学模型计算的前6阶固有频率结果进行对比分析，分析结果见表2。由表2可看出，利用本文建立的高速转台固有频率表达式求出的前6阶固有频率与ANSYS Workbench仿真软件的仿真结果基本相符，其中前2阶的误差较低只有2.63%与1.95%，随着阶数的增加误差逐渐增大，最大误差出现在第3阶与第4阶，达到6.18%与5.82%。ANSYS Workbench仿真软件计算转台模型更接近于真实情况，适用于求解结构复杂的转台系统。而理论计算时，是将高速转台模型简化成具有轴向力的转轴模型，根据对转轴模型进行解算得出的前6阶固有频率，所以会与有限元仿真结果存在一定偏差。

表2 转台有限元仿真和理论计算的前6阶固有频率的对比

通过对图7中转台结构前6阶模态振型提取分析，得到模态振型：1阶时模态振型为左右轴套及框架绕z轴发生扭转振动；2阶时模态振型为左右轴套及框架绕x轴发生扭转振动；3阶时模态振型为左右轴套及框架在y轴方向上前后同向振动；4阶时模态振型为左右轴套及框架绕z轴发生扭转振动；5阶时模态振型为左右轴套及框架绕x轴发生扭转振动；6阶时模态振型为左右轴套及框架互为反向绕z轴发生扭转振动。

图7 高速转台简化模型的前6阶模态

4 结 论

1) 通过对高速转台模型边界条件的设置得到了固有频率表达式，计算前6阶固有频率为118.63～ 768.32 Hz。将高速转台简化模型导入仿真软件，选择Block Lanczos模块对转台进行提取，得到的前6阶固有频率为121.63～805.83 Hz，误差率均小于6.18%，建立的高速转台固有频率表达式合理。

2) 将探测负载、电机、驱动器等部件作为负载加载在简化的模型上进行分析，通过转台应力变化云图和位移变化云图看出最大应力值与位移量均分布在负载内框表面上。最大位移量为2.227 75×10-2mm，最大应力为δmax=12.158×106Pa，该应力值大于要求的安全系数值7.036×107Pa。

3) 仿真发现探测负载部件作为载荷对模型静力学计算结果影响较大，是造成最大应力和位移均分布在负载内框上的原因。进一步将关键的外协部件作为仿真分析的结构与主结构相关联，发现应力变化与位移变化分布，为高速转台结构拓扑优化提供参考依据。