面向多尺度决策形式背景的粒结构模型

陈应生，李进金，2，林荣德 ，陈东晓

1(华侨大学 数学科学学院 计算科学福建省高校重点实验室，福建 泉州 362021)2(闽南师范大学 数学与统计学院，福建 漳州 363000)

1 引 言

在分析大量复杂信息时，基于有限的认识能力，人们通常会将庞大复杂的信息按照各自特点划分为若干较为简单的块.被分出的每个块就可以当作一个信息粒，以信息粒为单位，来分析处理复杂信息，这种方法称为粒计算.自Zadeh[1，2]提出信息粒化的概念以来，粒计算得到了广泛的关注[3-5]，随着人工智能及大数据分析研究的不断深入，粒计算理论得到不断的完善和发展，并且在数据处理、机器学习、人工智能、图像处理、模式识别等领域中具有广泛的应用[6-13].

粗糙集是粒计算的经典模型，Yao在文献[9]提出的利用等价关系构造信息粒的方法被广泛的应用，由于人们处理信息的不同深度导致信息认识的不同粒度，Wu-Leung 在文献[14]首次提出了多尺度决策信息系统，通过粒度转换函数，给出了不同尺度间信息粒之间的转化方法，并讨论系统的知识获取和最优尺度的选择方法.随后，文献[15]提出不同属性拥有不同尺度的推广模型.文献[16]提出了多尺度多决策的信息系统模型，并详细讨论决策属性不同尺度间的粒度转化，以及基于决策优先的最优尺度选择.文献[17-19]系统研究了不完备的多尺度决策信息系统模型，结合证据理论方法，讨论了该系统的信息粒度、粗糙近似、知识提取和最优尺度组合的选择方法.

利用分区进行信息造粒，这种方法过于严格，为了拓宽其应用，很多学者提出了推广的模型，主要有覆盖粗糙集模型[20]、模糊粗糙集[21]、形式背景[22-29]等等，其中形式背景是一个典型的推广.文献[22]指出形式概念分析是由对象集、属性集以及它们之间的二元关系组成的完备格，通过二元关系定义算子，从而形成概念格.文献[23-26]研究了形式背景概念格的生成方法、属性约简以及决策形式背景的协调性和属性约简.文献[27]提出了粒协调的概念，讨论决策形式背景的粒协调性质.文献[28]系统比较决策形式背景的各种协调的关系.文献[29]讨论了概念格与覆盖粗糙集的关系.指出形式背景和覆盖粗糙集可以互相转化.

在复杂信息和庞大数据中，形式背景产生的概念格十分复杂，因此，简化概念，获得适当规模大小的概念格是形式背景分析的重要问题之一，本文把多尺度信息系统的粒度转化函数推广到形式背景上来，引入多尺度形式背景，研究该系统的性质，以此为基础，建立多尺度决策形式背景的理论框架，并研究它的协调性以及最优尺度选择.

本文后面的安排如下.第2节介绍形式背景与决策形式背景的基本知识、各种协调性、以及它们的区别与联系；第3节引入多尺度决策形式背景，并讨论其粒结构和不同粒度间的粒度转化关系、粗糙近似、不同尺度对应形式背景的各种协调关系；第4节引入多尺度决策形式背景，并研究各种协调的传递性，以及最优尺度选择，并给出具体的算例；最后，我们总结这篇文章.

2 相关工作与基础知识

针对多尺度形式背景问题，文献[30]研究了多标记形式背景下的粒规则，其中要求每个对象在第i个标记Li下的取值是唯一的，这样一个标记下的形式背景对应于论域的一个划分，标记的每个取值以及取该值的对象全体匹配构成一个粒标记概念，即对任意的y∈Li，(f-1(y)，y)是一个概念(这里f-1(y)表示取值为y的对象全体)，由于它满足f(f-1(y))=y.但对于集值信息系统或覆盖信息系统，对象的标记取值可能不唯一，这时任意的y∈Li，不一定满足f(f-1(y))=y，从而(f-1(y)，y)未必是一个概念.

Wu-Leung在文献[14]中首次建立多尺度标记信息系统的粒计算模型，引入一个粒转换函数来刻画不同尺度间的信息粒关系，但在具体的应用中，属性往往构成覆盖而不是划分，形式背景是对论域覆盖的深入研究，文献[29]中详细讨论覆盖与形式背景的联系.

为了使多尺度理论更适用于大数据和复杂信息的应用，本文把信息系统的粒度转换函数推广到形式背景上来，建立多尺度形式背景的粒计算模型.文献[30]中的多标记形式背景模型为本文的特殊情况.

为了简化表达，在本文中，我们把形式背景记为FC，决策形式背景记为FDC，多尺度形式背景记为MCFC，多尺度决策形式背景记为MCFDC.

本节我们介绍形式背景与决策形式背景的基本概念、性质和协调性.

2.1 形式背景

定义1[23].设(U，A，I)为一个形式背景(记为FC)，其中U={x1，x2，…，xn}为有限非空对象集，我们称之为论域，A={a1，a2，…，am}为有限非空属性集，I为U和A之间的一个二元关系，如果(x，a)∈I，则称x具有属性a，否则，称x不具有属性a.

如果把(x，a)∈I表示为1，把(x，a)∉I表示为0，则形式背景就可以表示为一个布尔矩阵，记之为MI=(cij)n×m，其中：

设X⊆U，B⊆A，定义如下运算规则：

X*={a∈A|∀x∈X，(x，a)∈I}，B*={x∈U|∀a∈B，(x，a)∈I}.容易得到：

X*={a∈A|X⊆a*}=∩x∈Xx*，B*={x∈U|B⊆x*}=∩a∈Ba*.

如果，∀x∈U，x*≠∅，x*≠A且∀a∈A，a*≠∅，a*≠U，则称(U，A，I)是正则的，下面我们所讨论的FC都是正则的.

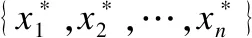
若X*=B，B*=X，则称(X，B)是一个概念，(U，A，I)的所有概念记之为L(U，A，I).

LU(U，A，I)表示L(U，A，I)的概念外延构成的一个格，LA(U，A，I)表示由L(U，A，I)的概念内涵构成的一个格.

显然，任意的X⊆U，(X**，X*)，是概念，同理任意的B⊆A，(B*，B**)也是概念，并且：

(X，B)=∪x∈X(x**，x*)，(X，B)=∩a∈B(a*，a**)

所以由对象粒概念(x**，x*)和属性粒概念(a*，a**)通过并交运算可以生成FC的全体概念格.

对于(X1，B1)，(X2，B2)∈L(U，A，I)，定义运算:

(X1，B1)∧(X2，B2)=((X1∩X2)，(B1∪B2)**)

(X1，B1)∨(X2，B2)=((X1∪X2)**，B1∩B2)

在文献[24，25]中，类似于粗糙集中的上下近似概念，对于任意的X⊆U，B⊆A，定义如下近似算子:X□={a∈A|a*⊆X}，X◊={a∈A|a*∩X≠∅}；B□={x∈U|x*⊆B}，B◊={x∈U|x*∩B≠∅}.

2.2 决策形式背景

定义2[25].设S=(U，A，I，D，J)为FDC，其中(U，A，I)与(U，D，J)是两个FC.

如果(X，B)∈L(U，A，I)，(Y，C)∈L(U，D，J)，X⊆Y，且Y≠U、∅，称“B→C”是一个命题.

本文*A，**A表示(U，A，I)下的运算，同理*D，**D表示(U，D，J)下的运算.

决策形式背景由于系统复杂，对于它的协调性讨论也是一个重要课题，下面介绍3种常用的协调性，并讨论他们之间的关系.

定义3.设S=(U，A，I，D，J)是一个FDC:

1)[25].∀(Y，C)∈L(U，D，J)，若存在(X，B)∈L(U，A，I)，满足X=Y，则称S是强协调的，记为L(U，A，I)≤L(U，D，J).

2)[25].∀(Yi，Ci)∈L(U，D，J)，若存在(Xi，Bi)∈L(U，A，I)，使Xi⊆Yi，且Yi≠Yj时，有Xi≠Xj，则称S是弱协调的，记为L(U，A，I)≼L(U，D，J).

3)[27].x∈U，若有x**A⊆x**D成立，则称S关于对象x是局部粒协调的，若S对所有对象都是局部粒协调的，则称S是粒协调的.

文献[28]详细讨论3种协调性之间的联系，

1)强协调可以推出弱协调，但反之不成立；

2)由粒协调不能推出弱协调，反之也不成立；

3)强协调可以推出粒协调，反之不成立.

针对弱协调的判断方法，文献[25]给出了弱协调的等价定义.

推论1.L(U，A，I)≼L(U，D，J)⟺存在单射f：LU(U，D，J)→LU(U，A，I)，满足对∀Y∈LU(U，D，J)，有f(Y)⊆Y.

特别地，如果LU(U，D，J)构成论域的一个划分时，则粒协调就可以推出弱协调.

定理1.设S=(U，A，I，D，J)是粒协调的FDC，且{d*D|d∈D}

构成论域U的一个划分，则有L(U，A，I)≼L(U，D，J).

证明：我们利用定义3的推论1来证明.

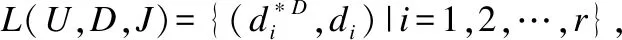
3 多尺度形式背景

3.1 多尺度形式背景

多尺度信息系统理论由Wu-Leung于文献[14]中首次提出，文献[15]提出了推广的模型.根据文献[14，15]的定义，对任意的属性a∈A，a的m个尺度记为a1，a2，…，am，其中ak：U→Vk，Vk为a在第k个尺度下的值域，并且对于1≤k≤m-1，存在一个满射gk，k+1：Vk→Vk+1，使得ak+1=gk，k+1∘ak，即对任意的x∈U，有ak+1(x)=gk，k+1(ak(x))，称gk，k+1为属性ak到ak+1的粒度转换函数.

上述定义要求ak：U→Vk是单值满射的，但在具体的应用中，ak：U→Vk往往是多值的，即ak：U→P(Vk)，其中P(Vk)是Vk非空子集的全体，同样的，我们要求对于1≤k≤m-1，也存在一个满射gk，k+1：Vk→Vk+1，使得ak+1=gk，k+1∘ak.

由此，我们提出如下多尺度形式背景的定义.

定义4.设(U，A，I)={(U，Ak，Ik)|k=1，2，…，m}为多尺度形式背景(记为MCFC)，其中A有m个尺度A1，A2，…，Am，相应地I也有m个尺度I1，I2，…，Im，并且每个(U，Ak，Ik)(k=1，2，…，m)都是一个FC，而且对任意的1≤k≤m-1，存在满射映射gk，k+1：Ak→Ak+1，使得对任意的∀x∈U，有x*Ak+1=gk，k+1(x*Ak)，gk，k+1称为属性集Ak到Ak+1的粒度转换函数.

定理2.设(U，A，I)为一个MCFC，则对任意的x∈U，k∈{1，2，…，m-1}，有x**Ak⊆x**Ak+1.

证明：由于x**Ak={y∈U|x*Ak⊆y*Ak}，对任意的y∈x**Ak，有x*Ak⊆y*Ak，故而x*Ak+1=gk，k+1(x*Ak)⊆gk，k+1(y*Ak)=y*Ak+1，由x**Ak+1={y∈U|x*Ak+1⊆y*Ak+1}，所以y∈x**Ak+1，因此x**Ak⊆x**Ak+1.

注：由于任一概念(X，Bk)∈L(U，Ak，Ik)，有(X，Bk)=∪x∈X(x**Ak，x*Ak)，所以(x**Ak，x*Ak)是(U，Ak，Ik)中最细的信息粒.

定理2表明，在MCFC中，对应于较小尺度的最细信息粒较为精细.

并且，由于x**Ak⊆x**Ak+1，所以“x*Ak→x*Ak+1”是一个命题，说明，在较大尺度下最精细的命题可以由较小尺度下的命题推出.

特别地，当多尺度形式背景每个尺度对应的背景构成论域的一个划分时，上述命题就是文献[30]定义的粒标记规则.

定理3.设(U，A，I)为MCFC，则以下结论成立.

1)|Ak|≤|Ak+1|，其中|Ak|表示Ak中属性的个数；

2)a∈Ak，b∈Ak+1若gk，k+1(a)=b，则a*Ak⊆b*Ak+1；

3)∀b∈Ak+1，x∈b*Ak+1，存在a∈Ak，使得x∈a*Ak⊆b*Ak+1；

4)∀b∈Ak+1，若(gk，k+1(b))-1=Bk，则b*Ak+1=∪a∈Bka*Ak.

证明：

1)直接由粒度转换函数gk，k+1的定义可得.

2)∀x∈a*Ak，有a∈x*Ak，由于gk，k+1(x*Ak)=x*Ak+1，所以b=gk，k+1(a)∈x*Ak+1，故而x∈b*Ak+1，因此a*Ak⊆b*Ak+1.

3)∀b∈Ak+1，有b∈x*Ak+1，由gk，k+1(x*Ak)=x*Ak+1，所以存在a∈x*Ak，使得gk，k+1(a)=b，由(2)得a*Ak⊆b*Ak+1，所以x∈a*Ak⊆b*Ak+1.

4)对任意的a∈Bk，有gk，k+1(a)=b，所以a*Ak⊆b*Ak+1，故而∪a∈Bka*Ak⊆b*Ak+1，另一方面，对∀x∈b*Ak+1，有b∈x*Ak+1，由于(gk，k+1(b))-1=Bk，存在a∈Bk，使得gk，k+1(a)=b，由b∈x*Ak+1和gk，k+1(x*Ak)=x*Ak+1，所以a∈x*Ak从而x∈a*Ak，所以x∈∪a∈Bka*Ak，故而b*Ak+1⊆∪a∈Bka*Ak，所以b*Ak+1=∪a∈Bka*Ak.

注：定理3说明

1)MCFC对应尺度k的形式背景(U，Ak，Ik)，任意的a∈Ak，(a*Ak，a**Ak)是一个概念，当Ak构成论域的一个划分时，有a**Ak=a，此时(a*Ak，a)就是文献[30]所提的标记概念.

2)若(gk，k+1)-1=Bk，则有b*Ak+1=∪a∈Bka*Ak，

所以，当每个尺度的属性集都构成论域的划分时，定义4就是文献[30]所提的多标记背景定义.

3)如果gk，k+1(a)=b，则 “a**Ak→b**Ak+1”是一个命题，当每个尺度的形式背景都构成论域 的划分时，有a**Ak=a，b**Ak+1=b，所以命题“a**Ak→b**Ak+1”简化为“a→b”就是文献[30]中所提的对象如果在属性a下的值相等，则在属性b下的值也是相等的.

定理4.设(U，A，I)为MCFC，则有以下结论成立.

1)任意(Y，C)∈L(U，Ak+1，Ik+1)，一定存在(X，B)∈L(U，Ak，Ik)，使得X⊆Y，即“B→C”是一个命题；

2)任意(X，B)∈L(U，Ak，Ik)，一定存在(Y，C)∈L(U，Ak+1，Ik+1)，使得X⊆Y，即“B→C”是一个命题.

证明：

1)任意的(Y，C)∈L(U，Ak+1，Ik+1)，满足Y*Ak+1=C，并且C*Ak+1=Y，对任意的b∈C，存在a∈A，使得a*Ak⊆b*Ak+1，所以Y=C*Ak+1=∩b∈Cb*Ak+1⊇∩a∈Ba*Ak=B*Ak，取(B*Ak，B**Ak)∈L(U，Ak，Ik)，X=B*Ak，即可.

2)任意的(X，B)∈L(U，Ak，Ik)，满足X*Ak=B，并且B*Ak=X，对任意的a∈A，存在b∈C，使得a*Ak⊆b*Ak+1，所以B*Ak=∩a∈Ba*Ak⊆∩b∈Cb*Ak+1=C*Ak+1，取(C*Ak，C**Ak)∈L(U，Ak+1，Ik+1)，Y=C*Ak+1即可.

定理4说明，在MCFC中，较大尺度规模下的一个结论，总可以由较小尺度下的条件推得.

3.2 多尺度形式背景的粗糙近似算子

MCFC对应尺度k的FC为(U，Ak，Ik)，∀X⊆U，Bk⊆Ak，根据近似算子的定义，有:

X□k={a∈Ak|a*Ak⊆X}，X◊k={a∈Ak|a*Ak∩X≠∅}；

B□k={x∈U|x*Ak⊆Bk}，B◊k={x∈U|x*Ak∩Bk≠∅}.

定理5.设(U，A，I)为MCFC，则以下结论成立:

1)gk，k+1(X□k)⊇X□k+1；

2)gk，k+1(X◊k)⊆X◊k+1；

3)如果gk，k+1(Bk)=Bk+1，则有B□k⊇B□k+1；

4)如果gk，k+1(Bk)=Bk+1，则有B◊k⊆B◊k+1.

证明：

1).对任意的b∈X□k+1，则有b*Ak+1⊆X，∀a∈(gk，k+1b)-1，则gk，k+1(a)=b，由定理3(2)，a*Ak⊆b*Ak+1，故而a*Ak⊆X，故而(gk，k+1(X□k+1))-1⊆X□k，因此gk，k+1(X□k)⊇X□k+1.

2)∀a∈X◊k，有a*Ak∩X≠∅，设b=gk，k+1(a)，由定理3(2)，a*Ak⊆b*Ak+1，故b*Ak+1∩X≠∅，因此gk，k+1(X◊k)⊆X◊k+1.

3)∀x∈B□k+1，有x*Ak+1⊆Bk+1，根据gk，k+1(x*Ak)=x*Ak+1以及gk，k+1(Bk)=Bk+1，故而x*Ak⊆Bk，所以x∈B□k，因此B□k⊇B□k+1；

4)∀x∈B◊k，有x*Ak∩Bk≠∅，由gk，k+1(x*Ak)=x*Ak+1及gk，k+1(Bk)=Bk+1，所以x*Ak+1∩Bk+1≠∅，故而x∈B◊k+1，从而B◊k⊆B◊k+1.

3.3 多尺度形式背景尺度间的协调关系

如果把(U，Ak，Ik，AK+1，Ik+1)当作一个FDC，由定理2有x**Ak⊆x**Ak+1，根据定义3粒协调的定义，有如下结论成立.

定理6.设S=(U，A，I)为MCFC，则(U，Ak，Ik，Ak+1，Ik+1)是粒协调的.

例1.(U，Ak，Ik，Ak+1，Ik+1)未必是弱协调的，如表1所示的MCFC(U，A，I)=(U，{A1，A2}，{I1，I2})，其中:

A1={a，b，c，d，e}，A2={g，h，k}

粒度转换函数g12：A1→A2为:

形式背景的布尔矩阵表如表1所示.

表1 多尺度决策形式背景1Table 1 Multi-scale formal context 1

经计算，L(U，A2，I2)={(U，∅)，(12，h)，(13，g)，(24，k)，(1，gh)，(2，hk)，(∅，A)}；L(U，A1，I1)={(U，∅)，(2，be)，(13，a)，(4，d)，(1，ac)，(∅，D)}，由于不存在单射f：LU(U，D，J)→LU(U，A，I)，满足对任意的Y∈LU(U，D，J)，有f(Y)⊆Y，所以，(U，A1，I1，A2，I2)不是弱协调的.

定理6及例1这表明多尺度形式背景较小尺度对于较大尺度，只能满足粒协调，不能满足弱协调，更不能保证强协调.

4 多尺度决策形式背景

定义5.设S=(U，A，I，D，J)为一个多尺度决策形式背景(记为MCFDC)，这里(U，A，I)={(U，Ak，Ik)|k=1，2，…，m}为一个MCFC，D≠Ai(i=1，2，…，m)，且(U，D，J)是一个FC.

由定义5可得，一个MCFDC包含m个FDC，把对应第k(k=1，2，…，m)尺度的FDC记为Sk=(U，Ak，Ik，D，J).

定理7.设S=(U，A，I，D，J)为MCFDC，(Y，C)∈L(U，D，J)，若(Xl，Bl)∈L(U，Al，Il)，使得Bl→C是一个命题，则对任意的k≤l，存在(Xk，Bk)∈L(U，Ak，Ik)，使得Bk→C也是一个命题.

证明：由定理4直接可得.

定理7表明，如果较粗的尺度规模下能够成立的，则在较细的尺度规模下也一定成立.

4.1 多尺度决策形式背景的协调性

设S=(U，A，I，D，J)为MCFDC，第k尺度的FDC记为Sk=(U，Ak，Ik，D，J)，首先我们讨论粒协调，由定理2及定理6，易得如下定理.

定理8.设S=(U，A，I，D，J)是MCFDC，则有以下结论成立.

1)Sk关于x∈U是局部粒协调的充要条件是x**Ak⊆x**D，Sk是粒协调的充要条件是对任意的对象都是局部粒协调的；

2)如果Sk关于x是局部协调的，则对任意的l≤k，Sl关于x也是局部协调的；

3)如果Sk是粒协调的，则对任意的l≤k，Sl也是粒协调的.

由定理8可得，MCFDC的粒协调满足传递性，例2说明MCFDC的强协调与弱协调并不一定满足传递性，例2.弱协调不一定具有传递性.

如表2所示的MCFDCS=(U，A，I，D，J)，其中(U，A，I)为例1中表1对应的MCFC，决策属性集为D={X，Y，Z}，系统对应的布尔矩阵为表2.

表2 多尺度决策形式背景2Table 2 Multi-scale formal decision context 2

由例1的结论，得(U，A1，I1，A2，I2)不是弱协调的，即L(U，A1，I1)≼L(U，A2，I2)不成立，由于L(U，A2，I2)=L(U，D，J)，所以L(U，A1，I1)≼L(U，D，J)不成立.

由例2说明，弱协调不一定具有传递性，同理可以得到强协调也不一定具有传递性.

特别地，当决策背景形成一个划分时，下面定理说明，弱协调也具有传递性.

定理9.设S=(U，A，I，D，J)是MCFDC，并且{d*D|d∈D}构成U的一个划分，如果L(U，Ak+1，Ik+1)≼L(U，D，J)，则有L(U，Ak，Ik)≼L(U，D，J).

证明：利用定义3的推论1来证明.

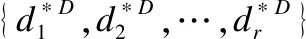
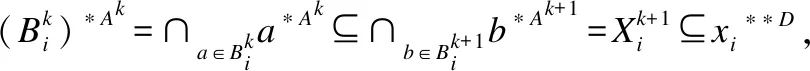
4.2 多尺度决策形式背景的最优尺度选择

设S=(U，A，I，D，J)是一个MCFDC，较小尺度对应的FDC所表达的知识的精度较高，但却需要花费较多时间和精力去了解知识，而较大的尺度虽然表达的知识比较粗糙，但却可以花费较少的时间和精力去了解知识，在具体的应用过程中，我们希望利用较少信息得到理想的决策，由此，提出MCFDC的最优尺度选择.

由于在多尺度决策形式背景中，强协调不具有传递性，粒协调具有传递性，在决策是划分的情况下，弱协调也具有传递性，所以本节只讨论保粒协调的最优尺度选择和保弱协调的最优尺度选择.

4.2.1 粒协调下的最优尺度选择

定义6.设S=(U，A，I，D，J)为一个MCFDC，若S1是粒协调的，则称S是粒协调的，若存在k∈{1，2，…，m}，使得Sk是粒协调的，但Sk+1不是粒协调的，则称k是粒协调最优尺度.

定义7.设S=(U，A，I，D，J)为一个MCFDC，x∈U，若存在k∈{1，2，…，m}，使得Sk关于x是局部粒协调的，但Sk+1关于x不是局部粒协调的，则称k是关于x局部粒协调最优尺度.

例3.求表3所示的MCFDC的保持粒协调得最优尺度.

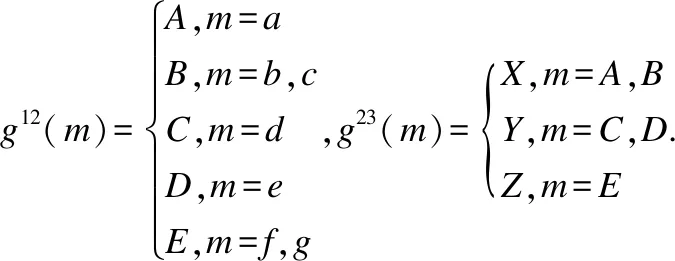
形式背景的布尔矩阵表如表3所示.

表3 多尺度决策形式背景3Table 3 Multi-scale formal decision context 3

经计算，可得：

1)1**D={1}，2**D=4**D={2，4}，3**D={3}；

2)1**A3={1，3}，2**A3=4**A3={2，4}，3**A3={3}；

3)1**A3={1}，2**A3=4**A3={2，4}，3**A3={3}.

所以尺度2是粒协调的最优尺度选择，并且该系统是粒协调的.对于局部粒协调，对象2，3，4局部粒协调的最优尺度是3，而对象1局部粒协调的最优尺度是2.

4.2.2 弱协调下的最优尺度选择

在MCFDC中，对于弱协调，通常是不保持传递性的，由定理9，当决策是划分时，弱协调也具有传递性，所以我们可以只讨论决策是划分时的保弱协调的最优尺度选择.

定义8.设S=(U，A，I，D，J)为一个MCFDC，并且L(U，D，J)构成论域的一个划分，若S1是弱协调的，则称系统S是弱协调的，更进一步，如果L(U，Ak，Ik)≼L(U，D，J)，但L(U，Ak+1，Ik+1)≼L(U，D，J)不成立，则称k是S的保弱协调的最优尺度.

例4.求表3所示的MCFDC的保弱协调的最优尺度.

经计算得:

L(U，D，J)={(∅，D)，(1M)，(24，P)，(3，Q)，(U，∅)}；L(U，A3，I3)={(∅，A3)，(13，Y)，(124，X)，(3，XY)，(24，XZ)，(U，∅)}.L(U，A2，I2)={(∅，A2)，(1，CD)，(13，D)，(234，B)，(3，ABD)，(24，BE)，(∅，A)}(U，∅)}.经计算，L(U，A3，I3)≼L(U，D，J)不成立，L(U，A2，I2)≼L(U，D，J)，所以第2尺度是保弱协调的最优尺度.

定理10.设S=(U，A，I，D，J)是一个MCFDC，当L(U，D，J)构成论域的一个划分时，并且系统S是粒协调的，如果k是粒协调的最优尺度，l是弱协调的最优尺度，则k≤l.

证明：由于决策构成一个划分，由定理1得，该多尺度决策形式背景也是弱协调的，所以存在弱协调的最优尺度，Sk是粒协调的，所以Sk也是广义协调的，所以k≤l.

5 总 结

多尺度信息系统的粒度转换函数刻画了多粒度信息从粗到细的特点，本文将这个粒度转换函数推广引入到FC中，建立了MCFC粒计算模型，以此来描述MCFC不同尺度之间的概念信息粒关系，不同尺度间粗糙近似算子的关系，以及不同尺度对应形式背景的协调性.在此基础上，引入MCFDC，并讨论它的协调传递性，通过分析，强协调和弱协调都不一定满足传递性，粒协调满足传递性，特别地，当决策是划分时，弱协调也满足传递性.最后，我们分别研究了MCFDC保持粒协调和弱协调的最优尺度选择，并给出具体的算例.本文建立了MCFDC的理论框架，推广了多尺度决策信息系统和多粒度形式背景的粒计算模型，未来，我们将研究MCFDC的规则提取和引入多尺度多决策的形式背景.