环形电流磁场分布及磁感线基于C++的数值模拟

李 超，洪 倩，杨雪冰,陈 锐,孙彦东,梁来力

(南阳理工学院 数理学院，河南 南阳 473000)

任意形状的通电线圈产生的磁场原则上都可以根据毕奥-萨伐尔定律进行求解，然而严格的解析解往往不能轻易地得到。哪怕对于简单的环形电流，一般教科书上也只是给出了中轴线上的磁感应强度分布，对于非轴线上的磁场，由于涉及复杂的椭圆积分[1]，很难得到解析解，这个时候借助计算机进行数值计算就显得非常合适。

1 环形电流的磁场分布

任意形状的载流线圈总可以等价为若干段电流元的叠加，每一段电流元在整个空间激发的磁场都遵循毕奥-萨伐尔定律[2]：

(1)

图1 环形电流示意图

(2)

考虑到环形电流产生的磁场对称性，选择柱坐标对电流元进行展开，可以得到：

(3)

空间某一个场点P可以表示为：

(4)

电流元到场点P的矢量可以表示为：

(5)

根据对称性，P点的磁感应强度分布也具有轴对称性，即当ρ和z一定时，任意φ角位置的磁感应强度的大小均相等。因此不妨将P点取在oxz平面，即P点的坐标满足φ=0，则此时根据(1)-(5)式联立可以解得P点磁感应强度沿x、y、z轴的分量为：

(6)

(7)

(8)

2 磁感应强度的数值模拟

(6)、(7)、(8)式即为任意点P的磁感应强度的分量形式，可以借助计算机辅助进行数值计算，既可以使用成熟的Matlab软件[3]，也可以使用更为基础的C++进行编程。

假设环形电流的半径a=0.1 m，通有的电流强度为I=1A，选择不同的(ρ,z)根据(6)、(7)、(8)式即可以计算得到不同空间位置的磁感应强度的分量，总的磁感应强度大小可以表示为：

(9)

在空间中随机选择一系列的点，通过数值计算得到的磁感应强度大小如表1所示。

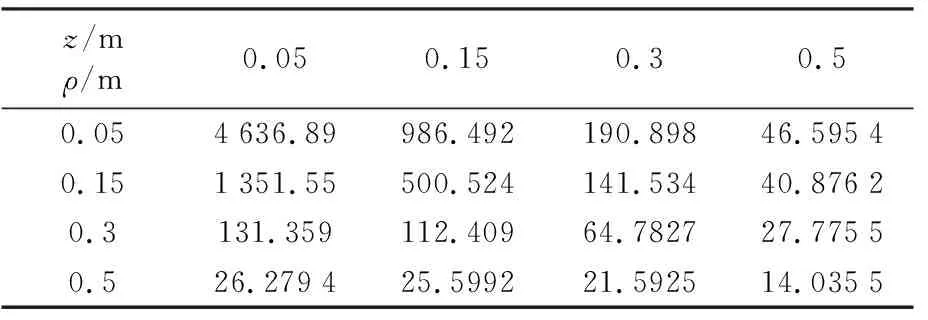
表1 不同空间位置(ρ,z)的磁感应强度大小(×10-9 T)

3 磁感线的描绘

3.1 磁感线的描绘方法

如图1所示，xz平面和环形电流存在两个交点，这两个交点即为圆环的一条直径。在这条直径上任意选择一系列点，并且令这些点相对圆心O对称，这样描绘出来的磁感线将呈对称分布。

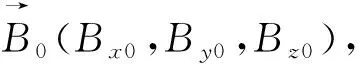
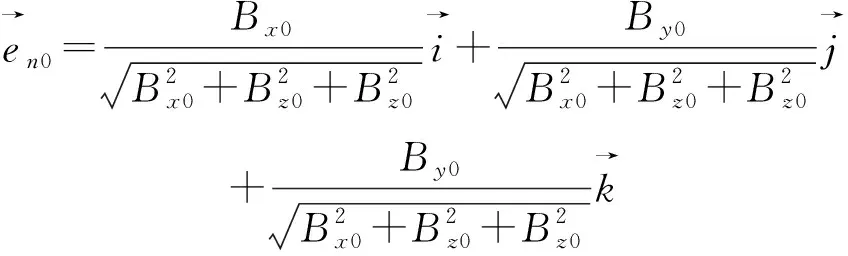
(10)

利用上式得到的单位矢量代入(11)式计算得到下一个点A1(x1,y1,z1)点的坐标：

(11)

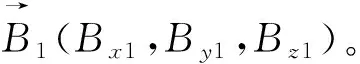
3.2 磁感线描绘方法的验证

为了验证上节介绍的磁感线描绘方法的可行性及正确性，可以选择一个已知的曲线用上述方法进行测试。不妨选择简单的幂函数：

y=x3

(12)

图2 磁感线描绘方法的验证

由于选择的步长为0.000 1，所以这些点分布非常密集，并且和真实的函数(12)对应的红色曲线完全重合，由此可见磁感线的描绘方法是完全可行的。

3.3 环形电流磁感线的描绘

前面研究了磁感线的描绘方法并对该方法的正确性给出了证明，下面将利用该方法得到环形电流的磁感线描绘。仍然取环形电流的半径为0.1 m，电流强度为1A。

由于环形电流的磁场符合轴对称分布，因此只需取xz平面为代表即可。如图3所示，左边红色点表示电流在该点是流出的，右边的红色叉号表示该点电流是流入的。在这两点之间对称的取11个点作为起点，每个点对应一条磁感线的分布，总共描绘了11条磁感线。

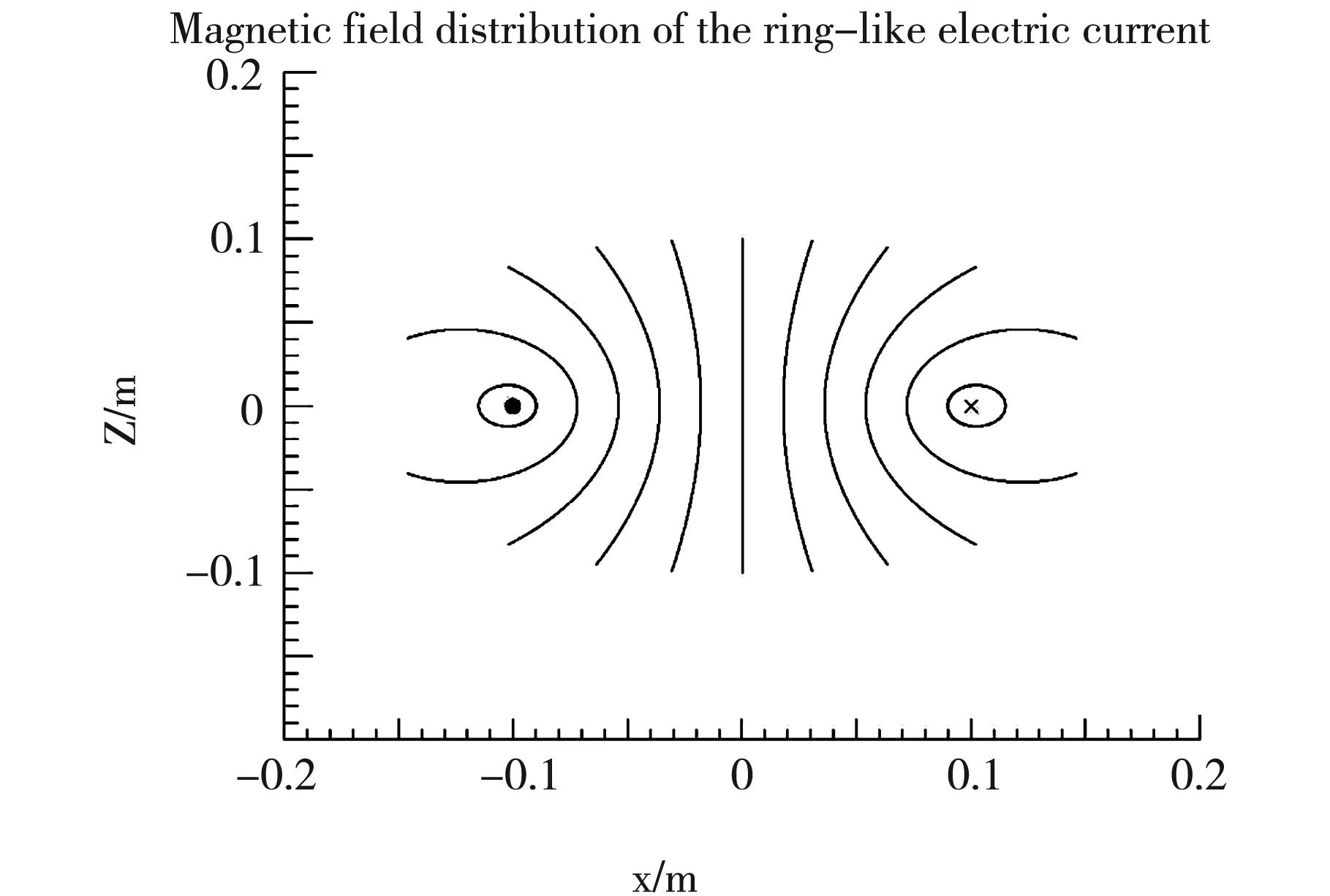
图3 环形电流磁感线的描绘

4 结 语

首先从毕奥-萨伐尔定律推导得到了环形电流在整个空间激发的磁场分布；进而选取了若干点对环形电流的磁场进行了数值计算；研究得到了磁感线描绘的一般方法并对该方法进行了验证；最后给出了环形电流在空间所激发磁场的磁感线描绘。由于该磁感线描绘方法具有一般性，因此可以拓展至其他任意类型的磁场分布。