基于FORTRAN的双色圆偏振激光场光电离的电子涡旋研究

韩轶凡，于伟威，韩斯宇，成珈仪，郭伊彤

(辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)

随着超短激光脉冲技术的发展，超短激光脉冲与原子、分子相互作用的光电子动力学研究受到了广泛的关注。近年来超短激光脉冲与原子、分子相互作用的光电子动力学研究取得了不错的进展，研究发现可以应用非次序双电离来说明相干电子动力学[1]；双色圆偏振阿秒紫外激光场中电子动量分布在同旋和反旋情况下都表现出涡旋结构[2]。利用两束含有时间延迟的反旋圆偏振阿秒脉冲使氦原子进行单光子电离，使其产生的光电子动量分布具有涡旋结构，两束脉冲间的时间延迟变化会使这个涡旋结构发生旋转[3]。光电子动量分布成为探索原子和分子结构的新工具[4]。研究发现双色圆偏振激光脉冲作用下He+的光电子动量分布呈现涡旋结构，在双色圆偏振激光场中，两束激光脉冲的相对相位发生变化会使涡旋发生旋转，并用阿秒微扰电离理论对结果进行了解释[5]。

实验上用两束具有时间延迟的反旋激光脉冲探测到钾原子多光子电离的光电子，得到三维光电子动量分布。在微扰极限下观察到了具有旋转对称性的电子涡旋[6]。理论研究发现双色反旋圆偏振激光场中激光脉冲旋向和角频率对He+光电子动量分布的涡旋结构有很大影响，并用阿秒微扰电离理论对研究结果进行了分析[7]。He+在双色圆偏振激光场中光电子动量分布不对称是由He+在双色圆偏振激光场中的光电离过程导致的[8]，光电子动量分布的涡旋结构在一个周期内会随两束激光脉冲之间的时间延迟的变化而旋转。然而以往的研究偏向于讨论原子或分子的电离过程对形成光电子动量分布的影响，对电子涡旋的轨迹和旋转方向的讨论很少。

激光与物质的相互作用不仅可以通过实验来求证，还能以计算机为工具，用理论模型和数值模拟来演示。利用FORTRAN语言模拟组合圆偏振激光场中He+光电子动量分布发现光电子动量分布受激光脉冲波长和旋向的影响[9]。本文基于FORTRAN语言编程，用计算机数值模拟双色反旋圆偏振激光场中He+光电子动量分布。这种方法既能避免进行操作复杂的实验，又能很好解决部分高校实验仪器不足或实验设备落后的问题。

1 理论方法

主要的理论方法是通过求解二维含时薛定谔方程研究双色反旋圆偏振激光场中He+光电子动量分布中的电子涡旋。研究过程中的计算与推导都要利用FORTRAN语言编程来实现，通过程序计算模拟得到我们所需的数据。二维含时薛定谔方程表示为

(1)

式中ψ(x,y,t)是随时间变化的电子波函数，px和py分别是电子在x和y方向的动量，Ex(t)和Ey(t)分别是x和y方向的激光场。软核库仑势V(x,y)为

(2)

软核参数为a=2和b=0.169，对应于He+的第一电离能为2a.u.。

两束激光脉冲表示为

(3)

(4)

E0是强度为0.12 a.u.(5×1014W/cm2)的激光脉冲的振幅，ω1和ω2为脉冲角频率，脉冲包络为f(t)=sin(2πt/T)，持续时间t=10τ且

1τ=2π/ω1。

本文研究中涉及的两种激光场分别为

E1,2=E1(t)+E2(t-Δτ)

(5)

E2，1=E1(t-Δτ)+E2(t)

(6)

用虚时演化法得到基态波函数，并用分裂算符法求解二维含时薛定谔方程。任意时刻波函数：

(7)

积分网格长度为409.6 a.u.，时间步长为0.05 a.u.，为了防止波包从边界反射而产生的非物理效应，在每个时间步，波函数乘以cos1/8面具函数，吸收范围为|x,y|=150 a.u.～|x,y|=204.8 a.u.。

当波函数传播到最后时刻tf时，最后时刻的波包为ψ(x,y,tf)，电离部分为[1-M(r)]ψ(x,y,tf)，面具函数如下式：

(8)

式中β=1 a.u.，设边界rB=15 a.u.。将电离波函数傅立叶变换到动量空间，得到光电子动量分布形式为：

D(px,py,tf)=|ψ(px,py,tf)|2

(9)

式中ψ(px,py,tf)可以写成：

ψ(px,py,tf)=

(10)

2 结果与讨论

本文研究了由两束反旋圆偏振激光脉冲组成的双色反旋圆偏振激光场下的He+光电离过程中的电子涡旋，用FORTRAN语言编程模拟He+的光电子动量分布。我们发现反旋圆偏振激光场中He+的光电子动量分布呈现涡旋结构。当激光脉冲频率ω2=ω1=2.28 a.u.时，此时λ2=λ1=20 nm，如图1(a)所示，由He+的光电子动量分布图可以看到在这种情况下动量分布呈双叶涡旋结构。图1(b)为电场的矢势图，我们用矢量势反映电子涡旋的旋向。He+在激光脉冲频率ω2=ω1=2.28 a.u.时发生单光子电离，此时电子涡旋的旋向先由外向内旋转，后由内向外旋。

图1 (a)和(b)：分别对应ω2=ω1=2.28 a.u.时，He+在双色反旋圆偏振激光场中的动量分布，矢势图

图2 (a)和(c)：分别对应由双色反旋圆偏振激光场E1,2(t)的光电子动量分布图和三维矢势图；(b)和(d)：分别对应于双色反旋圆偏振激光场E2,1(t)的光电子动量分布图和三维矢势图，频率ω1=1.14 a.u.，ω2=2ω1=2.28 a.u.

我们用双色反旋圆偏振激光场来研究激光发射顺序对光电子动量分布中电子涡旋的影响。图2(a)中激光场是由先发射的一束左旋圆偏振激光，经过时间延迟Δτ=5 o.c.再发射一束右旋圆偏振激光组成，图2(b)激光场的组成为先发射一束右旋圆偏振激光，经过时间延迟Δτ=5 o.c.再发射一束左旋圆偏振激光。我们发现含有时间延迟的双色反旋圆偏振激光场E1,2(t)和E2,1(t)下He+的光电子动量分布分别如图2(a)和(b)所示。其中，时间延迟Δτ=5 o.c.，ω1=1.14 a.u.对应脉冲波长λ1=40 nm，ω2=2ω1=2.28 a.u.对应脉冲波长λ2=20 nm。可以看出，He+的光电子动量分布呈现出三瓣涡旋结构。从矢势图中不难看出两个电子涡旋还是有区别的，即图2(a)中的电子涡旋由外向内旋转，而图2(b)中的涡轨迹由内向外旋转。

在本文中我们用双色反旋圆偏振激光场E1,2(t)和E2,1(t)中的矢量势来反映电子涡旋变化的规律，并绘制了三维矢量势图，分别如图2(c)和(d)所示。我们用两束激光脉冲的矢势轨迹来反映电子涡旋的轨迹，通过对矢势的分析，从图2(c)和图2(d)可以看出，矢量势的旋转方向都随着时间的增加先向左旋转，第二束激光发射后向右旋转，两个矢量势的轨迹略有不同，图2(c)中矢势随时间增加由外向内旋呈逐渐收缩的趋势，图2(d)中矢势的变化规律与图2(c)正好相反。

我们改变了激光脉冲的频率使ω1=0.76 a.u.，ω2=3ω1=2.28 a.u.，对应的激光脉冲波长变为λ1=60 nm，λ2=20 nm，其他参数不变。在这种情况下我们得到的结果如图3所示，图3(a)和(c)分别是双色反旋圆偏振激光场E1,2(t)的光电子动量分布图和三维矢势图，图3(b)和(d)分别是双色反旋圆偏振激光场E2,1(t)的光电子动量分布图和三维矢势图。从图中可以看到光电子动量分布呈现四瓣涡旋结构。可以用阿秒微扰电离理论来解释这一现象[3]。图3(a)的涡旋结构中的四个瓣都呈现出由外向内旋的特征，而图3(b)中的四个瓣都呈现出由内向外旋的特征。图3(c)和(d)分别显示了双色反旋圆偏振激光场E1,2(t)和E2,1(t)的三维矢量势。图3(c)所示的矢势轨迹随着时间的增加向内收缩，而图3(d)所示的矢势轨迹随着时间的增加而向外扩展，图3(c)和(d)可以分别解释图3(a)和(b)所示的电子涡旋轨迹特征。

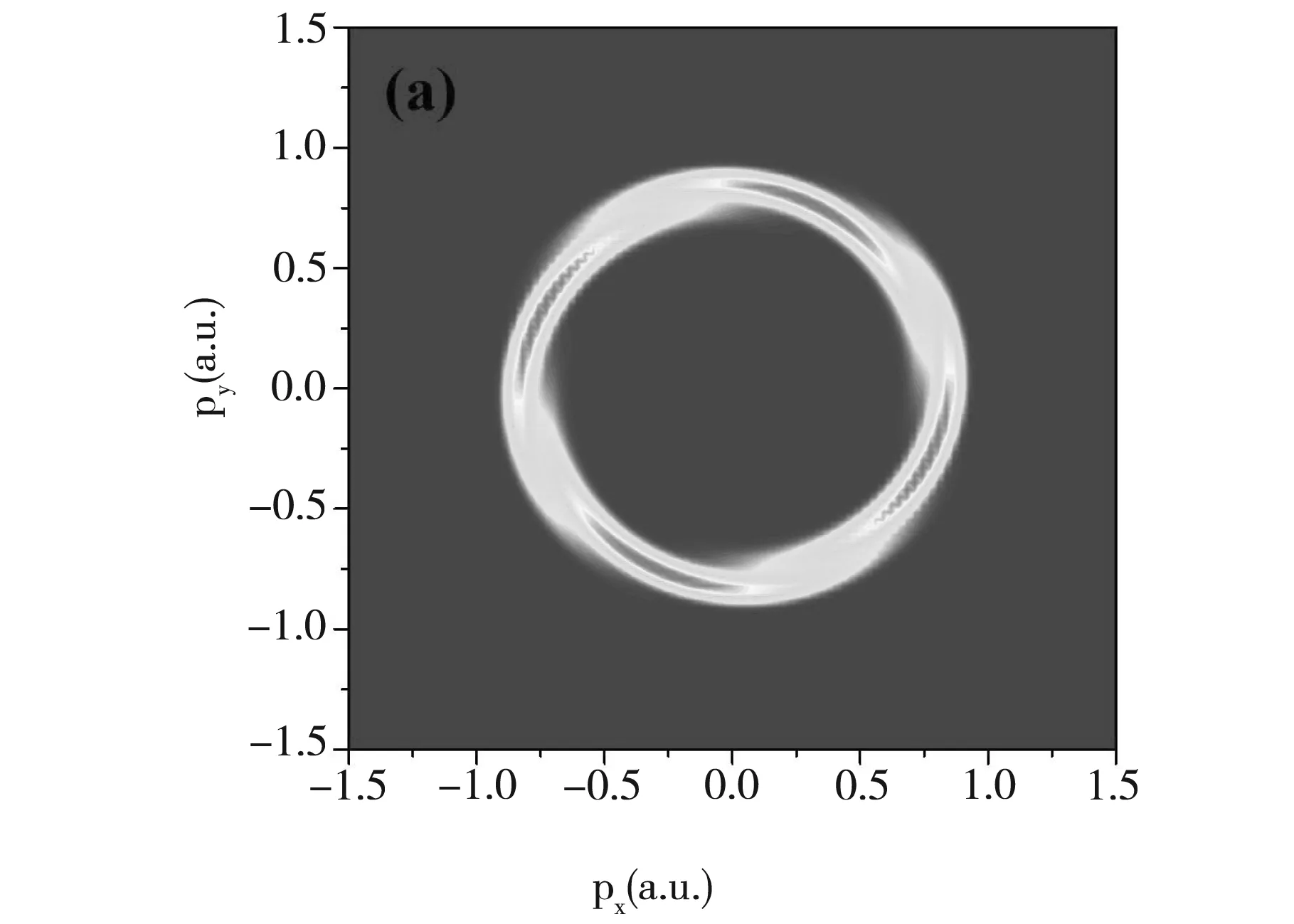
图3 (a)和(c)：分别对应由双色反旋圆偏振激光场E1,2(t)的光电子动量分布图和三维矢势图；(b)和(d)：分别对应于双色反旋圆偏振激光场E2,1(t)的光电子动量分布图和三维矢势图，频率ω1=0.76 a.u.，ω2=3ω1=2.28 a.u.

3 结 语

本文利用FORTRAN语言求解二维含时薛定谔方程，研究了ω2=ω1，ω2=2ω1和ω2=3ω1时双色反旋圆偏振激光场中He+光电离所产生的光电子动量分布及其电子涡旋。我们用两束激光脉冲的矢势轨迹来演示电子涡旋的轨迹，通过对矢势的分析发现在双色反旋圆偏振激光场中光电子动量分布呈涡旋结构。两束激光脉冲的时间延迟Δτ=5 o.c.，两束激光脉冲的发射顺序不同，He+光电离产生的电子涡旋的旋向不同，两束激光脉冲的发射顺序会影响电子涡旋，使其表现出由内向外扩展或由外向内收缩的相反趋势。