需求扰动信息不对称下的双渠道供应链生产定价决策
2021-07-07徐章一李文利丁龙晨芷
周 珺 徐章一 李文利 丁龙晨芷
(武汉理工大学物流工程学院 武汉 430063)
0 引 言
据艾瑞咨询的数据显示,2019年第三季度中国网络购物市场交易规模达2.3万亿元,较2018年同比增长22%.在“互联网+”和电子商务快速发展的背景下,很多企业越来越倾向于网上直销和传统零售渠道相结合的双渠道模式.
而随着供应链全球化、一体化的发展,生产运作所处的环境越来越复杂,对外部环境的变化也更加敏感,各种突发事件都会影响供应链的正常运行,导致市场需求的扰动.一般来说,零售商要比制造商能够更加准确得到市场需求的扰动信息.由于双渠道模式的运行,可能会加剧供应链的渠道冲突,损害零售商的利益,因此零售商对制造商的合作意愿会有所降低,需求扰动信息的共享程度也会有所削弱.需求扰动信息的不对称,还会产生偏离成本,因此,对于制造商而言,如何设计一套合理的契约机制,使得零售商真实地披露需求扰动信息,从而在考虑偏离成本的基础上制定最优的生产计划和定价决策尤为重要.
近年来,双渠道供应链的研究已取得大量理论和实证研究成果,这些成果主要集中在渠道选择、定价和协调三方面.在渠道选择和定价方面,Yang等[1-2]发现随着渠道竞争和冲突的加剧,零售价格和网上直销价格的定价竞争也愈演愈烈.张霖霖等[3]通过构建不同权力结构博弈模型探究双渠道价格一致策略.梁喜等[4]针对网上直销、代销和分销三种不同的双渠道模式进行制造商渠道选择和定价决策分析,研究表明在一定条件下网上直销和代销双渠道所获取的利润高于分销双渠道.王文宾等[5]构建了交叉销售下的制造商双渠道模型,并分析交叉销售效应对制造商定价的影响.在双渠道协调的研究方面,Wei等[6-7]通过改进的收入共享和成本分担契约对服务型制造商双渠道进行协调.唐润等[8]研究具有时间和温度等特殊因子的生鲜食品双渠道供应链,并设计批发价格契约对供应链进行协调.
目前,关于扰动管理的研究大多是基于扰动信息对称.彭静等[9]研究双渠道供应链下需求扰动对定价和生产决策的影响,并设计数量折扣契约、收益共享契约协调分散决策下的供应链系统.颜波等[10]考虑风险规避零售商主导下的供应链面临需求扰动时的最优决策,发现最优生产量在需求扰动下具有一定的鲁棒性.张玉春等[11]利用系统动力学方法设计收益共享契约,研究发现契约可以有效协调需求扰动下的闭环供应链.吴晓志等[12]考虑突发事件造成需求和生产成本的同时扰动,通过求解KKT条件得出不同扰动范围下的最优定价决策.
以上研究都是基于信息对称情况下的,但事实上,突发事件造成的市场需求扰动通常只有零售商能观察得到,而制造商无法获取准确的需求扰动信息.少数学者对信息不对称下的扰动管理进行了研究,黄松等[13]基于非线性需求函数,研究非对称信息下需求扰动对供应链的影响并设计契约显示机制.刘婷婷等[14]利用委托代理理论分析非对称生产成本对供应链效用的影响,并通过最优契约协调供应链.但以上文献所研究的供应链并不是双渠道供应链.
文中拟构建一个制造商双渠道为主导、零售商为跟随者的供应链,研究当突发事件造成市场需求扰动且扰动信息为零售商私有信息时,制造商如何设计契约机制,使得零售商真实地披露需求扰动信息,进而探讨需求扰动信息价值对供应链生产定价决策及性能的影响.
1 问题描述及基本模型
1.1 问题描述
制造商为主导的二级双渠道供应链的系统结构见图1.制造商不仅可以委托零售商进行产品的销售,以W的批发价卖给零售商,还可以以Pd的直销价直接销售给消费者.作为代理人的零售商则以Pr的零售价格卖给消费者.

图1 双渠道供应链系统结构
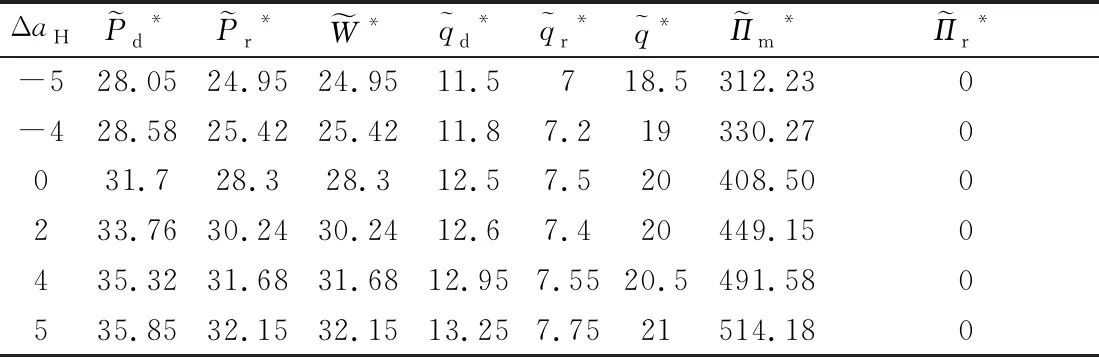
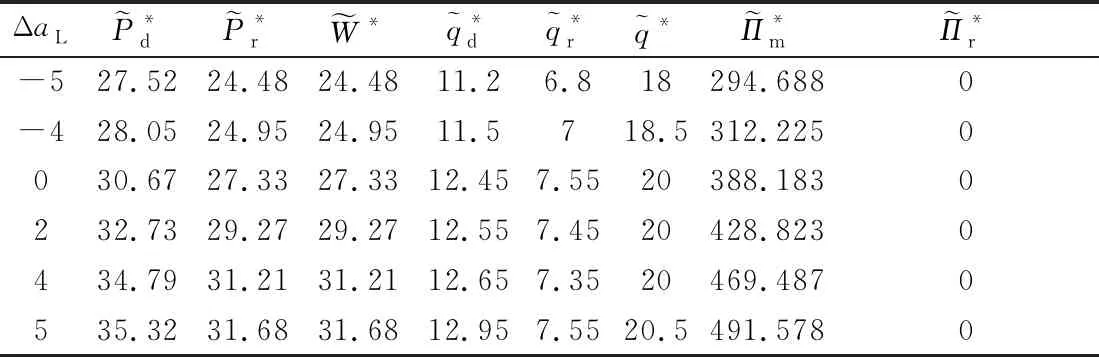
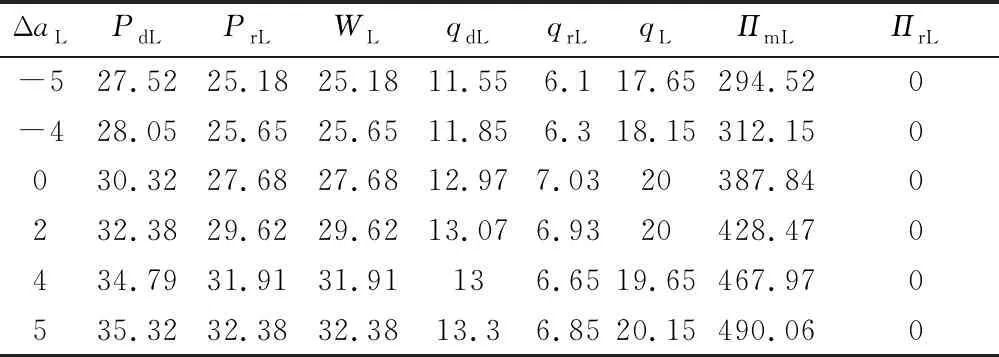
假定制造商和零售商之间构成Stackelberg博弈,制造商作为主导方,先制定产品的批发价格W、网上直销渠道价格Pd,零售商后决策零售价格Pr.双方都以自身利润的最大化为决策目标,设零售商的保留利润为零.制造商网上直销渠道和零售商传统零售渠道的需求函数分别为:qd=sa-Pd+λPr,qr=(1-s)a-Pr+λPd.其中,a为市场需求;s(0 当不存在需求扰动时,假设供应链所有信息对称,制造商生产成本为Cm,不考虑零售商销售成本、运输成本等成本,以制造商为主导的Stackelberg博弈模型为 maxπm=(W-Cm)qr+(Pd-Cm)qd s.t (Pr-W)qr≥0 约束条件表示零售商的利润不小于其保留利润.只有当约束条件为紧约束时,制造商的利润才能达到最大.通过逆向归纳法求导,容易得到无需求扰动时制造商和零售商的最优定价决策: 对应的最优订货量为 双渠道供应链总订货量为 此时,供应链的决策最优化问题可表示为 (1) (2) 定理1当需求发生扰动且扰动信息为对称信息时,双渠道供应链的定价和生产决策为 由式(2)可知,零售商的零售价格等于制造商的批发价格,因此零售商只能获得保留利润,而制造商获得整个渠道的利润.结合定理1可知,当需求扰动程度不大时,双渠道的最优生产数量随需求扰动的方向调整,但双渠道供应链的总生产数量与正常运营环境下的均衡决策一致,最优定价按需求扰动的方向进行调整.这表明初始的生产数量具有一定的鲁棒性.当需求扰动程度较大时,供应链的最优定价和生产决策都需要按照需求扰动的方向进行调整. 在供应链实际运作过程中,需求扰动信息一般为零售商私有,制造商无法获得准确的需求扰动信息.参考文献[15],假设制造商不知道市场需求扰动的大小,仅知道市场需求扰动有两种类型,分别为高需求扰动和低需求扰动,即Δa∈{ΔaH,ΔaL},且满足ΔaH>ΔaL.制造商虽然不知道需求扰动的真实信息,但知道ΔaH的概率为θ,ΔaL的概率为1-θ.其中:θ为制造商对于需求扰动情况的先验概率.将观察到高需求扰动的零售商称为高需求零售商,观察到低需求扰动的零售商称为低需求零售商.当市场需求发生扰动且扰动信息不对称时,双渠道的需求量和销售价格也会发生变化.当市场为高需求扰动时,关于价格的逆需求函数为 当市场为低需求扰动时,关于价格的逆需求函数为 式中:下标H、L分别为高需求扰动和低需求扰动. 对于制造商而言,需要设计一套合理的契约机制来诱导零售商通过选择契约披露真实的扰动信息.双方的博弈顺序为:①零售商观察到需求扰动为ΔaH或ΔaL;②制造商提供两种不同的批发价格契约{(qH,WH)}、{(qL,WL)}供零售商选择;③零售商根据观察到的需求扰动类型选择符合自身利润最大化的契约或者选择放弃.根据上述分析,制造商的决策问题为 maxπm=θ[(WH-Cm)qrH+(PdH-Cm)qdH-μ1(qrH+qdH-q*)+- μ2(q*-qrH-qdH)+]+(1-θ)[(WL-Cm)qrL+ (PdL-Cm)qdL-μ1(qrL+qdL-q*)+-μ2(q*-qrL-qdL)+] (4) 式中:不等式(5)、(6)表示激励相容约束,即高需求(低需求)零售商如实选择契约{(qH,WH)}({(qL,WL)})的利润不低于他模仿低需求(高需求)零售商选择契约{(qL,WL)}({(qH,WH)})所带来的利润.不等式(7)、(8)表示参与约束,即零售商选择契约时的利润不低于其保留利润. 由于ΔaH>ΔaL,不等式(5)和(8)仍然成立,但制造商利润将会增大,与WH(WL)是制造商的最优批发价矛盾.所以不等式(5)和(8)一定为紧约束.联立不等式(5)和(8),可得: (9) (10) 由式(9)~(10)可知:高需求零售商利用信息优势可以获得额外的信息租金.将式(9)、(10)代入目标函数式(4),分别对qrH+qdH≥q*且qrL+qdL≥q*、qrH+qdH≥q*且qrL+qdL≤q*、qrH+qdH≤q*且qrL+qdL≤q*三种情况进行讨论并通过求解可得定理2、定理3. 定理2当需求发生扰动Δa且扰动信息为高需求扰动时(ΔaH),双渠道供应链的定价和生产决策为 定理3当需求发生扰动Δa且扰动信息为低需求扰动时(ΔaL),双渠道供应链的定价和生产决策为 R1={(ΔaH,ΔaL)|ΔaL>(1-λ)r+2μ1(1-λ)} R2={(ΔaH,ΔaL)|ΔaH>2μ1(1-λ),(1-λ)r-2μ2(1-λ)<ΔaL≤(1-λ)r+2μ1(1-λ)} R3={(ΔaH,ΔaL)|-2μ2(1-λ)<ΔaH≤2μ1(1-λ),(1-λ)r-2μ2(1-λ)<ΔaL≤(1-λ)r+2μ1(1-λ)} R4={(ΔaH,ΔaL)|ΔaH>2μ1(1-λ),ΔaL≤(1-λ)r-2μ2(1-λ)} R5={(ΔaH,ΔaL)|-2μ2(1-λ)<ΔaH≤2μ1(1-λ),ΔaL≤(1-λ)r-2μ2(1-λ)} R6={(ΔaH,ΔaL)|ΔaH≤-2μ2(1-λ)} 为更好的验证需求扰动价值分析结果,结合算例,重点对需求扰动信息对称与不对称时的契约差异和利润差异两方面进行分析.主要参数赋值如下:a=50,ΔaH∈[-5,5],s=0.6,Cm=10,λ=0.5,μ1=3,μ2=2,θ=0.6,并令ΔaH-ΔaL=1.结合相关数据,不同扰动情形下的算例结果见表1~4. 表1 信息对称时高需求扰动供应链决策 表3 信息对称时低需求扰动供应链决策 表4 信息不对称时低需求扰动供应链决策 由表1~4可知,给定Δa,比较需求扰动信息对称与不对称的契约菜单: 不同扰动状态下的最优订货量和批发价见图3~4. 图3 高低需求扰动下最优订货量 图4 高低需求扰动下最优批发价 由图3可知,高需求零售商的定价、订货量与需求扰动信息对称时的相应范围的定价、订货量保持一致,这说明当市场为高需求扰动时,非对称需求扰动信息对供应链决策没有影响,高需求零售商的订货量也不会发生扭曲.而低需求扰动下,只有在(1-λ)r-2μ2(1-λ)<ΔaL≤(1-λ)r+2μ1(1-λ)时,最优订货量才与信息对称时一致.当扰动超出此范围,低需求零售商须通过减少订货量,提高零售渠道价格才能最大化供应链系统利润.这说明低需求零售商的订货量发生扭曲,从而影响供应链的整体效益. 由图4可知,制造商批发价格总体上随着订货量的增加而上升.由于生产计划具有一定的鲁棒性,市场需求的变化会影响制造商的定价决策.从图中可以发现,最陡峭的区间即为批发价的鲁棒区间.另外,当扰动信息对称时,高需求扰动下的批发价格总是高于信息不对称时的批发价格,而低需求扰动下则相反.这是由于高需求扰动时,零售商获得额外的信息租金;低需求扰动时,制造商向零售商提供更具吸引力的批发价以保证一定的订货量. 由表3~4可知,给定Δa,比较需求扰动信息对称与不对称的利润差异: 高需求扰动情形下的制造商和零售商利润见图5. 图5 高需求扰动状态下制造商和零售商利润 低需求扰动情形下的制造商利润见图6. 图6 低需求扰动状态下制造商利润 1) 当市场为高需求扰动时,非对称需求扰动信息对供应链决策没有影响. 2) 当市场为低需求扰动时,零售商订货量发生扭曲,只有当市场需求在一定范围内扰动时,需求扰动信息的不对称对双渠道供应链的订货生产不会产生影响. 3) 制造商根据需求扰动的范围设计不同的契约菜单供零售商选择,高需求零售商可以获得额外的信息租金,低需求零售商只能得到保留利润.由于制造商需要支付一部分信息租金以及承担订货量偏离造成的损失,因此信息不对称时的双渠道供应链利润小于信息对称时的利润,只有当需求扰动在一定范围时两种情形下的利润才相等. 未来将进一步研究需求扰动信息不对称时的供应链协调问题.1.2 基本模型
2 需求扰动信息对称下双渠道供应链决策
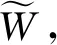
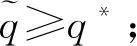
3 需求扰动信息不对称下双渠道供应链决策
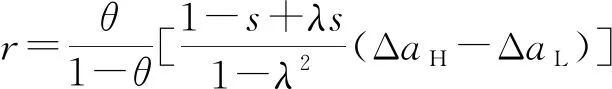
4 需求扰动信息价值分析
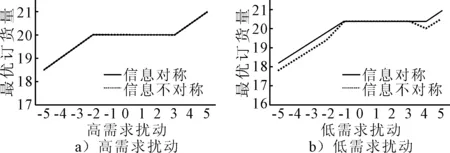
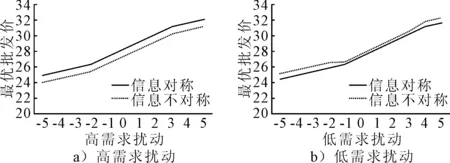
4.1 需求扰动信息对称与不对称下契约差异分析
4.2 需求扰动信息对称与不对称下利润差异分析

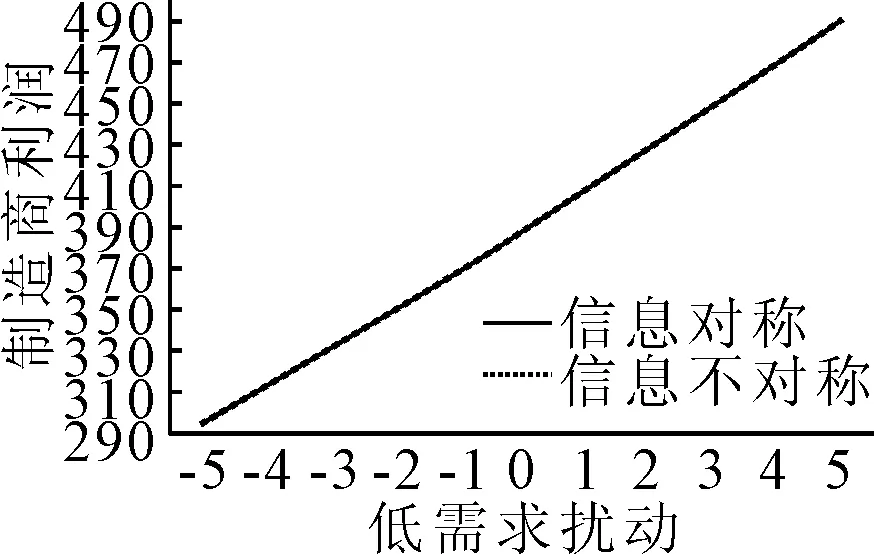
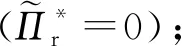
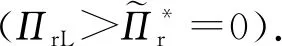
5 结 论
