轻质超高性能混凝土(LUHPC)梁抗弯性能试验

刘沐宇 赵 刚 丁庆军 张 强

(武汉理工大学道路桥梁与结构工程湖北省重点实验室1) 武汉 430070) (中铁大桥勘测设计院集团有限公司2) 武汉 430050)

0 引 言

高强混凝土已经广泛应用于土木工程结构，但其自重大、抗裂性能差等缺点制约了桥梁结构的跨越能力和耐久性能，高性能混凝土的轻质化研究是当前重要的研究热点.本课题组制备了一种轻质超高性能混凝土(lightweight ultra-high performance concrete，LUHPC)，它的基本力学性能为：抗压强度大于110 MPa，劈裂强度大于12 MPa，弹性模量大于3.8×104MPa，表观密度小于2 100 kg/m3.LUHPC作为一种新材料，对其展开抗弯性能分析十分必要.

目前许多学者已经开展了关于RPC梁、UHPC梁抗弯性能的研究.郑文忠等[1]进行了6根钢筋混凝土梁受弯性能试验，研究表明:RPC试验梁的开裂弯矩明显大于普通混凝土梁，计算其极限抗弯承载力应考虑受拉区RPC的拉应力贡献.孙明德等[2]开展了20根RPC梁抗弯试验，试验表明正截面抗弯计算应考虑受拉区钢纤维的拉结作用.文献[3-5]研究了超高性能混凝土梁正截面抗弯性能，结果表明超高性能混凝土梁的抗弯承载力计算应适当考虑受拉区拉应力的贡献；文献[6-8]研究了UHPC梁的裂缝发展规律及开裂弯矩的计算方法.研究表明:UHPC梁的开裂弯矩明显大于普通混凝土梁.LUHPC梁的抗弯性能和极限承载力计算公式目前没有针对性研究[9-11].

文中以配筋率、钢筋强度为变化参数，设计制作16根LUHPC梁，配筋率为0.3%、2.3%、4.2%、6.8%、8.7%，钢筋强度为HRB400、HRB500，同时制作了7根高强混凝土梁作为对比梁，开展LUHPC梁抗弯性能试验.研究了LUHPC梁的破坏形态、荷载-挠度曲线、配筋率和钢筋强度对于极限承载力、开裂弯矩和延性的影响规律，同时依据承载能力极限状态下跨中截面混凝土实测应变分布规律，提出了将受压区应力图形简化为三角形，并考虑受拉区混凝土拉应力贡献的抗弯承载力计算修正公式.

1 LUHPC梁抗弯试验方案

1.1 LUHPC材料性能

材料性能测试见图1，轻质超高性能混凝土以及高强混凝土配合比见表1，材料物理力学性能实测值见表2.

图1 LUHPC材料性能测试以及梁体浇筑

表1 LUHPC和高强混凝土配合比

本课题组研制的轻质超高性能混凝土的基本物理力学性能见表2.LUHPC立方体抗压强度大于110 MPa，劈裂抗拉强度大于12 MPa，弹性模量大于3.8×104MPa，密度小于2 100 kg/m3，表明LUHPC材料能够减小结构自重，同时也具有很好的物理力学性能.

表2 LUHPC和高强混凝土的基本力学性能

1.2 试验梁模型设计

以配筋率、钢筋强度为设计变量制作了16根LUHPC梁，同时制作了7根高强混凝土梁作为对比，各梁尺寸均为150 mm×250 mm×2 000 mm.为消除试验误差，每种配筋率的LUHPC梁制作两个.试件配筋率为0.3%、2.3%、4.4%、7.1%、8.8%.纵向钢筋采用HRB400、HRB500，为避免正截面计算时受压钢筋的影响，架立钢筋在跨中截断，试验梁编号以及设计参数见表3.

表3 梁体配筋表

1.3 加载方案及测点布置

试验采用四点对称加载，压力机施加的荷载即为本次试验所需采集的力，试验加载方式参照GB/T20152—2012《混凝土实验方法标准》进行，采用分级加载的方式，每级荷载预估为极限荷载的10%.在试验开始前首先进行预加载，用以消除个部件接触不均匀.为防止梁端点锚固破坏，两边各留100 mm，计算跨径为1 800 mm.现场加载图见图2a)，验梁模型配筋图、加载测点布置示意图见图2b).

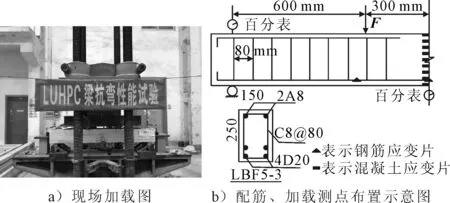
图2 现场加载图及试件横截面配筋详图

在梁体跨中截面沿梁高方向等距布置9个应变片用以测量各个加载阶段下截面应变分布.分别在纵向钢筋的三分点、中点布置钢筋应变片，测量钢筋的应变.在梁体的跨中和支点处布置位移计，测量各级荷载作用下竖向挠度.用裂缝观测仪记录每级荷载作用下裂缝的发展情况.

2 试验现象描述

16片LUHPC梁均发生弯曲破坏，经过计算，LUHPC梁配置HRB400级钢筋，当配筋率为小于0.33%时，发生少筋破坏，为 0.33%～8.21%时为适筋破坏，大于8.21%时为超筋破坏.本文给出三种典型的破坏模式实物图，见图3.

图3 LUHPC梁三种典型破坏破坏形态图

1) 试件LBF4-1发生少筋破坏.破坏始于受拉钢筋屈服，受压区LUHPC并没有压碎，破坏时在梁体跨中形成一条宽度约为5 mm的主裂缝.由于钢纤维的桥接作用，少筋梁开裂后并不会马上破坏，开裂荷载约为破坏荷载的70%.少筋梁的破坏经历了两个阶段：弹性工作阶段、钢筋屈服破坏阶段.弹性阶段：加载初期荷载-挠度曲线的斜率接近直线，并没有裂缝的开展；钢筋屈服破坏阶段：此阶段梁体出现第一条裂缝，开裂后的荷载-挠度曲线有明显的转折点，这意味着梁体的抗弯刚度有较大的变化，但是由于钢纤维的桥接作用，荷载可以继续增大，最后梁体破坏，表现出一定的延性.

2) 试件LBF4-2、LBF4-3、LBF4-4、LBF5-2、LBF5-3、LBF5-4均发生适筋破坏，这种破坏的主要特征是钢筋首先屈服，受压区LUHPC被压碎.适筋梁的破坏分为3个阶段：弹性工作阶段、裂缝发展阶段、钢筋屈服破坏阶段.弹性阶段：加载初期，荷载-位移曲线呈线性增长，此阶段并没有裂缝开展；裂缝的发展阶段：随着荷载的继续增加，梁底出现了第一条裂缝，此时梁体的刚度并没有明显减小，出现裂缝后钢筋承担的拉应力占比逐渐增大，随着荷载的继续增加，逐渐形成3～5条主裂缝，荷载挠度曲线斜率逐渐减小，当荷载超过到极限荷载的50%～65%时不会有新裂缝开展；破坏阶段：此阶段钢筋逐渐屈服，裂缝延梁高迅速发展，挠度急剧增大，受压区LUHPC压碎，荷载挠度曲线的斜率逐渐接近0，梁体因无法继续承担荷载而破坏.

3) 试件LBF4-5发生超筋破坏，梁体破坏始于受压区LUHPC被压碎，受拉钢筋并没有屈服，跨中截面受拉区最大裂缝宽度约为1 mm，破坏时挠度约为11 mm.超筋梁的破坏经历了三个阶段：弹性阶段、裂缝发展阶段和破坏阶段，前两个阶段与适筋梁相似，经历破坏阶段时纵向受拉钢筋并没有屈服，破坏始于受压区LUHPC被压碎，无法承担压应力.

3 LUHPC梁抗弯性能分析

3.1 LUHPC及钢筋应变分析

跨中混凝土应变分布规律是承载能力极限状态下简化应力分布模式的重要依据，23片试验梁在各级荷载作用下跨中混凝土应变均满足平截面假定，其中两片梁的应变变化规律见图4a)～b).由图4a)～b)可知：适筋梁破坏时，受压区轻质超高性能混凝土的压应变约为2 800×10-6；梁体在各个受力阶段下的截面应变分布接近平截面；由图4c)可知，跨中钢筋的荷载-钢筋应变曲线在梁体达到屈服之前，一直呈线性关系增长，在梁体出现第一条裂缝时，钢筋的应变-荷载曲线无明显转折点，梁体屈服之后，曲线有明显转折点，此时钢筋的应变约为(2 500～2 800)×10-6，钢筋同时达到了屈服强度.

图4 LUHPC及钢筋应变变化规律图

3.2 荷载-挠度曲线

荷载-挠度曲线可以直观的反应梁体破坏形态上的差别，本文给出典型配筋率梁的荷载-挠度曲线，并将相同配筋率下的LUHPC梁和高强混凝土梁为一组做出荷载-挠度曲线，见图5.

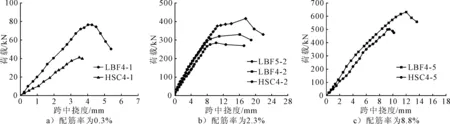
图5 少筋、适筋、超筋梁荷载-挠度曲线

由图5a)可知:LUHPC少筋梁的承载力比高强混凝土的大，同时破坏时表现出一定的延性，LUHPC梁的荷载挠度曲线斜率较大，这是因为钢纤维的掺入，使得梁体的抗弯刚度比高强混凝土大.

由图5b)可知:在相同配筋率下，承载力排序为：LBF5-2>LBF4-2>HSC4-2；LUHPC梁的荷载-挠度曲线的斜率比高强混凝土的大，这表明钢纤维的掺加能够提高梁体的抗弯刚度；配置不同强度钢筋的LUHPC梁的荷载-挠度曲线斜率无明显差别，这表明钢筋的强度不会显著影响梁体的抗弯刚度.

由图5c)可知:LUHPC梁的极限承载力比高强混凝土梁大；当梁体达到屈服荷载时，荷载挠度曲线斜率立刻变为负数，即两者的破坏形态都呈现脆性破坏.

3.2 配筋率、钢筋强度与LUHPC梁开裂弯矩和极限承载力的关系

图6为2种钢筋强度和5种配筋率对开裂弯矩、极限荷载的影响关系图.

图6 配筋率、钢筋强度与开裂荷载和极限承载力关系图

由图6a)可知:LUHPC梁的开裂弯矩随着配筋率的增大而增大；配置HRB500和配置HRB400钢筋开裂弯矩基本相同，即当配筋率相同时，钢筋强度对开裂弯矩没有显著影响，这是因为达到开裂荷载时，纵向钢筋没有屈服的原因所致.由图6b)可知:在适筋范围内，LUHPC梁的极限承载力随着配筋率的提高而提高，当配筋率为2.3%、4.2%、6.8%，钢筋为HRB400级时，LUHPC梁的极限承载力提高了26.9%～35.7%；LUHPC梁的极限承载力随着纵向钢筋强度提高而提高，相同配筋率下，HRB500级钢筋与HRB400级相比，LUHPC梁的极限承载力提高了10.5%～28.5%；相同配筋率下LUHPC梁的极限承载力比高强混凝土梁大.

3.4 配筋率与延性系数之间的关系

为了明确配筋率对于延性系数的影响规律，本文计算了其延性系数，并将延性系数与配筋率影响关系做成图，见图7.由图7可知，LUHPC梁的延性明显优于高强混凝土梁，这表明在混凝土中掺加钢纤维可以提高混凝土梁的延性；在适筋和超筋范围，延性系数随着配筋率的提高而减小.

图7 配筋率与延性系数关系图

4 LUHPC梁抗弯承载力计算修正公式

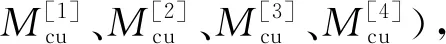
图8 极限状态下五种截面应力简化图式

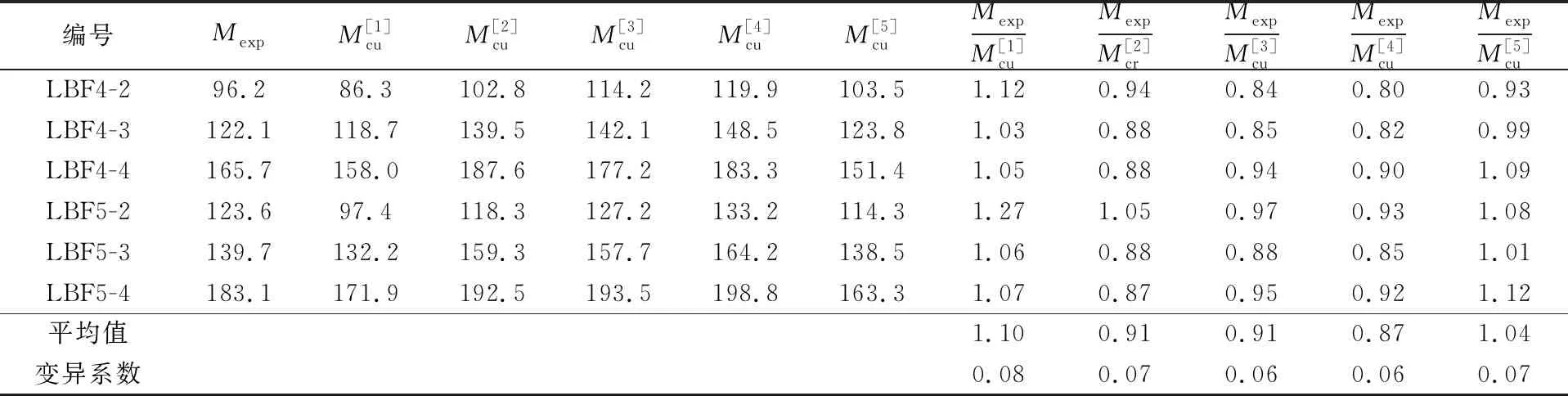
表4 LUHPC梁抗弯承载力试验值与各规范规程计算值 单位/kN·m

由图4a)～b)可知:适筋梁在承载能力极限状态下受压区顶端实测压应变为2 800×10-6，小于LUHPC峰值应变，对应的应力应变关系仍处于线性上升阶段，因此将受压区应力图形简化为三角形是合理的；极限状态下钢筋合力点下部混凝土由于裂缝开展较大，不能承受拉应力，因此受拉区的高度为(h0-c)，本文简化图式见图8e).根据力大小和合力点不变的原则，等效后将受拉区应力图形简化为矩形，拉应力的贡献为kftu，折减系数为k.适筋情况下，对受压区合力点取矩，极限状态的力平衡方程和弯矩平衡平衡方程为

(1)

(2)

式中：ftu为LUHPC的抗拉强度，取75%的劈裂抗拉强度；k为抗拉强度折减系数；h0为截面高度；fy为钢筋极限强度；fc为LUHPC轴心抗压强度；c为受压区高度；ρs为配筋率.

5 结 论

1) 当配筋率为2.3%、4.2%、6.8%，钢筋为HRB400级时，LUHPC梁的极限承载力提高了26.9%～35.7%，在相同配筋率下LUHPC梁的开裂弯矩和极限承载力均高于高强混凝土梁，其延性明显优于高强混凝土梁，配筋率为0.3%时，为少筋破坏，8.7%时为超筋破坏，适筋梁破坏时，裂缝分布呈现细而密的特点.

2) 相同配筋率下，HRB500级钢筋与HRB400级相比，LUHPC梁的极限承载力提高了10.5%～28.5%，开裂弯矩比较接近.

3) 将受压区应力图形简化为三角形，受拉区应力图形简化为矩形，其中抗拉强度的折减系数k为0.65，提出了LUHPC梁的极限承载力计算修正公式，试验值与理论计算值吻合较好，平均误差为4%，本文提出的计算公式具有较好的计算精度.