装配式T梁纵向连接方式比较及其影响因素研究
2021-07-07王沛源王向阳
任 鹏 王沛源 王向阳
(武汉理工大学交通学院1) 武汉 430063) (天津天怡建筑规划设计有限公司2) 天津 300110) (武汉理工大学土木工程与建筑学院3) 武汉 430070)
0 引 言
装配式T梁在高速公路桥中应用越来越多,其裂缝或者其他结构破坏往往发生在连接处,而现阶段对于装配式T梁的纵向连接受力性能研究较为缺乏[1-6].因此,分析各种纵向连接接缝结构的力学性能有助于装配式结构桥梁的发展,对桥梁设计也提供了一定的理论支持.
文中采用ANSYS软件建立装配式T梁模型,以某高速公路装配式桥梁为背景,通过改变连接接缝构造,对比分析不同纵向连接形式下的受力影响因素问题,以此得到较优的纵向连接构造.
1 工程概况
以某高速公路2×40 m装配式T梁桥为工程背景,此桥梁上部结构为变截面T梁,横向布置五片T梁,截面尺寸见图1.
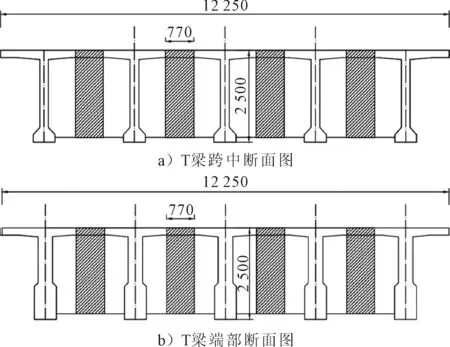
图1 桥梁断面图 (单位:mm)
混凝土均都采用C50型号混凝土;桥面铺装采用8 cm厚沥青混凝土.预应力钢筋采用抗拉强度标准值fpk=1 860 MPa,公称直径d=15.2 mm的低松弛高强度钢绞线.
2 装配式T梁纵向连接模型
2.1 纵向连接形式
装配式梁常用和新型的纵向连接构造形式主要有以下几种:竖直接缝、斜接缝、L形或阶梯形接缝、齿块形接缝,见图2[7-13].
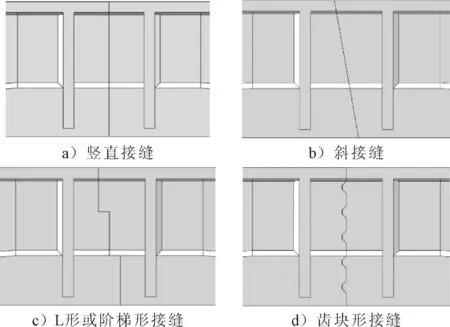
图2 纵向连接接缝示意图
2.2 纵向连接模型
1) 混凝土建模 使用SOLID95单元模拟桥梁的混凝土结构,桥梁的混凝土结构有限元模型见图3.
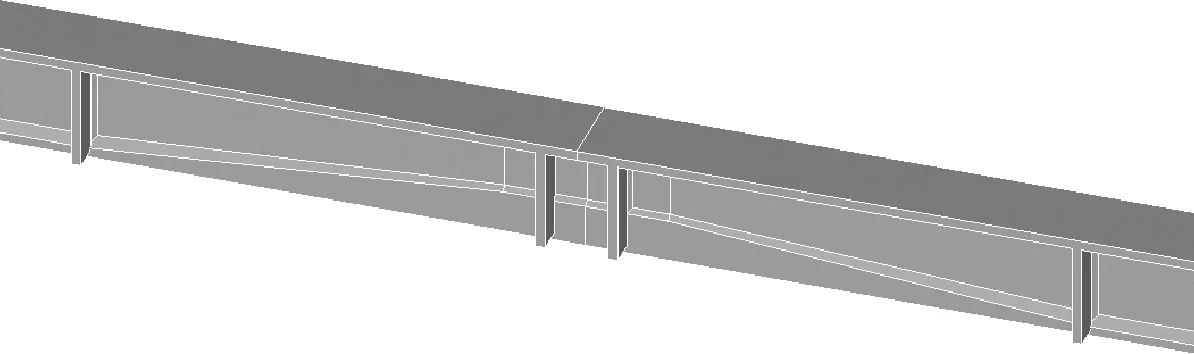
图3 混凝土实体模型
2) 预应力钢筋建模 在ANSYS软件中采用“实体力筋法”进行预应力的模拟.预应力钢筋建模的实常数见表1.
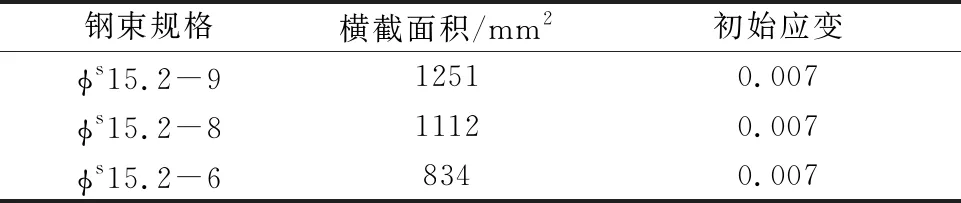
表1 预应力钢筋实常数
3) 纵向连接接缝处理 为了使纵向连接的湿接缝的受力性能区分于预制混凝土T梁,对湿接缝的相邻混凝土采用约束方程法进行刚性连接,使相邻的预制T梁在湿接缝截面自由度相同并且相邻节点通过刚性连接,即受到的变形与应力相同,以此分析不同接缝形式下的接缝处力学性能.
3 纵向连接影响因素计算分析
3.1 斜接缝影响因素分析
对于斜接缝的影响因素主要为倾斜角度的影响,对比分析的为5°、7.5°、10°、12.5°、15°五种倾斜角度.其连接接缝的应力云图见图4.
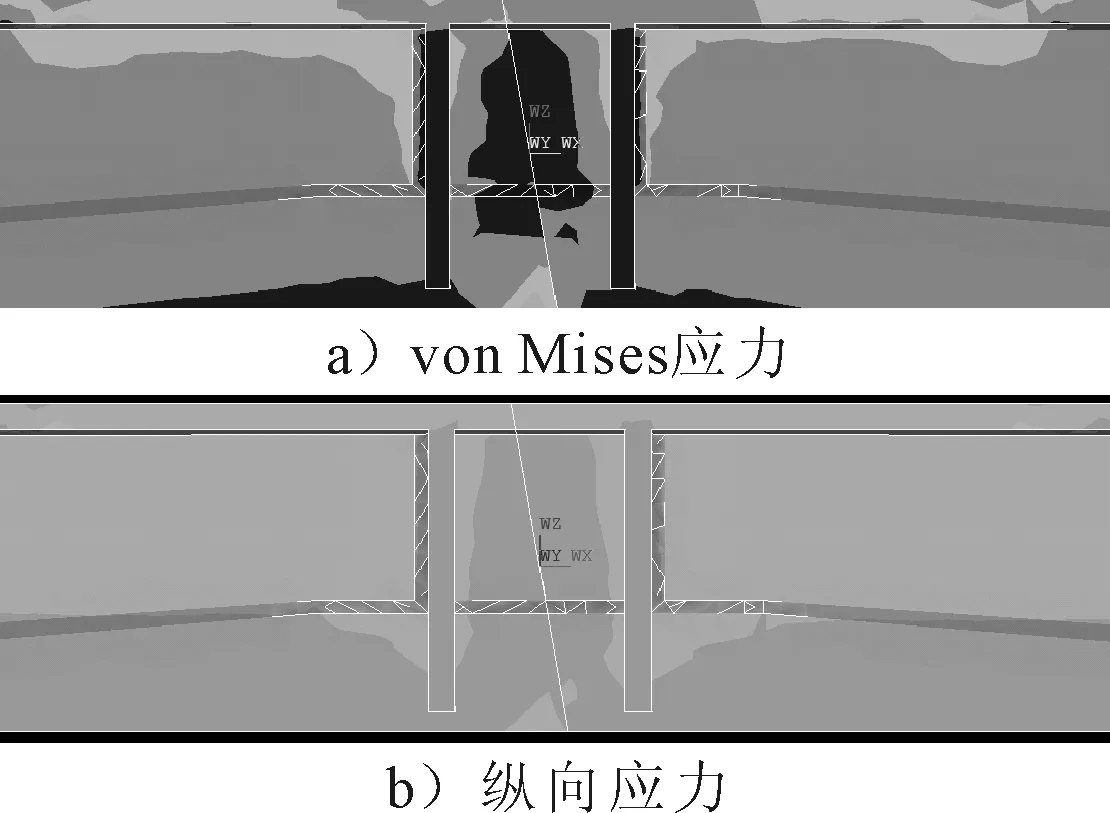
图4 斜接缝应力云图
1) 竖向最大变形分析 通过对五种模型竖向变形云图与最大竖向变形分析,其结果几乎相同.最大竖向变形均在T梁的跨中位置附近,距离跨中截面偏向T梁端部1 m处.结果见表2.

表2 竖向最大变形
由表2可知,随着倾斜角度的增加,其跨中附近最大竖向变形无明显变化.
2) 连接接缝处上、下缘纵向正应力分析 对五种模型的纵向应力云图与连接处上、下缘应力分析,得知不同的倾斜角度对于连接处上、下缘的应力有明显影响,其具体结果见表3.
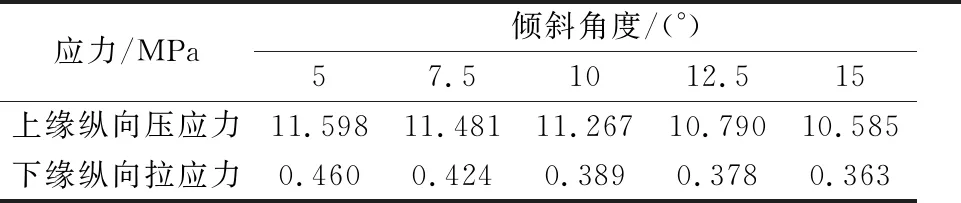
表3 连接处上下缘应力
由表3说明,随着连接接缝的倾斜角度的增加,其上下缘的纵向正应力均有所减小.过总体应力变化与减小幅度来看,改变斜接缝的倾斜角度是有利于改善装配式T梁的受力性能.
3) 腹板应力分析 对五种模型的应力云图与计算数据分析,得知不同的倾斜角度对于腹板的应力有明显影响,具体结果见表4,为了使结果对比明显,以5°的斜接缝为类比项,其他倾斜角度的斜接缝为对比项,对比图为图5.

表4 腹板应力
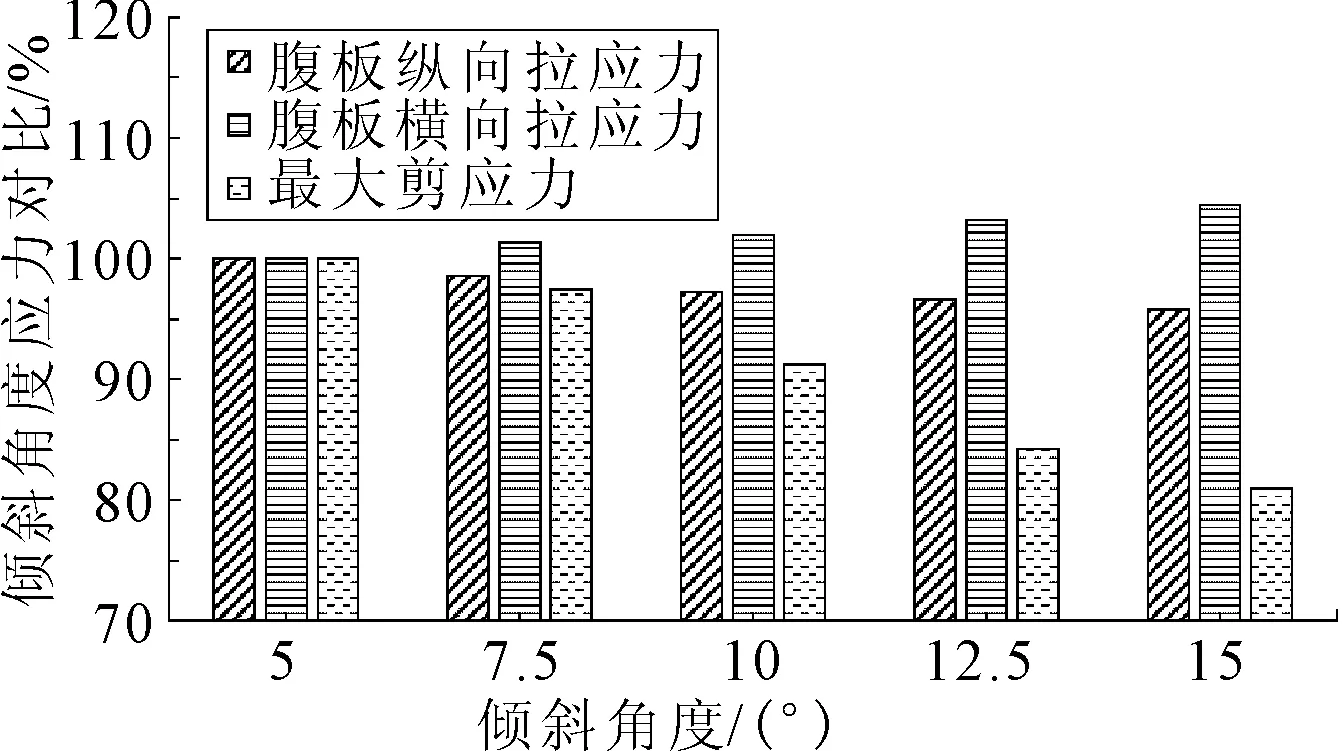
图5 连接处腹板应力对比图
由表4和图5可知,横向压应力随着倾斜角度的增大而有所增加,增幅约为4.3%;纵向拉应力随着倾斜角度的增加有所减小,减幅约为4.4%.最大剪应力随着角度的增大而减小,并且减小幅度较大,约为19%.
通过剪应力与腹板正应力的分析得知,剪应力减小,斜接缝的倾斜角度使得一部分的剪切应力由相互连接的斜截面承担,一部分剪应力由连接面挤压应力的形式表现,从而使得剪应力有所减小.
随着倾斜角度的增加,连接上、下缘的纵向正应力与腹板剪应力等关键应力均有所减小. 为了分析在斜接缝倾斜角度大于15°时的受力性能,对20°的斜接缝进行有限元模拟,对几种关键应力的计算分析见表5.

表5 20°斜接缝应力 单位: MPa
由表5可知,当倾斜角度大于15°时,在斜接缝的倾斜角度从15°增加至20°,其应力降幅已经趋于稳定,对于斜接缝的受力性能的影响较小,但是会增加施工难度与施工工期,不利于装配式T梁的施工.
综上所述,考虑以上因素与实际施工中操作难度,斜接缝连接形式应选择15°为较优选择.
3.2 L型或阶梯型接缝影响因素分析
3.2.1阶梯面数量影响性分析
选择200 mm的阶梯面宽度,分别对单阶梯面、双阶梯面与三阶梯面进行有限元模拟,对三种模型分别命名为L1、L2与L3.具体连接形式见图6,其应力云图见图7.
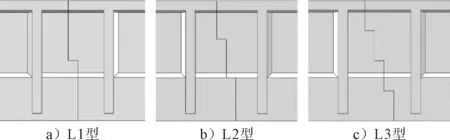
图6 阶梯形接缝种类

图7 L形或阶梯形接缝应力云图
1) 连接接缝处应力分析 通过对三种模型应力云图与应力数据分析,得知三种连接方式对装配式T梁的连接处受力性能有一定的影响,具体分析结果见表6.
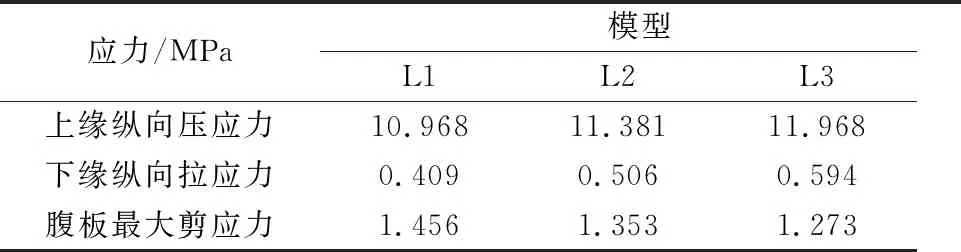
表6 连接接缝处应力
由表6可知,改变阶梯数量,影响最大的为下缘纵向拉应力,最大值与最小值的差距幅度在大约45%;其次为腹板剪应力,差距幅度在大约12%;上缘纵向压应力差距幅度最小,约为9%.
2) 阶梯面应力分析 L形或阶梯形接缝的阶梯面是延T梁纵向的水平面,是阶梯形接缝连接形式与其他连接形式的最主要的结构区别,主要分析应力为三种:湿接缝截面的最大剪应力、延阶梯面法向方向的竖向压应力与延T梁纵向的拉应力,具体分析结果见表7.
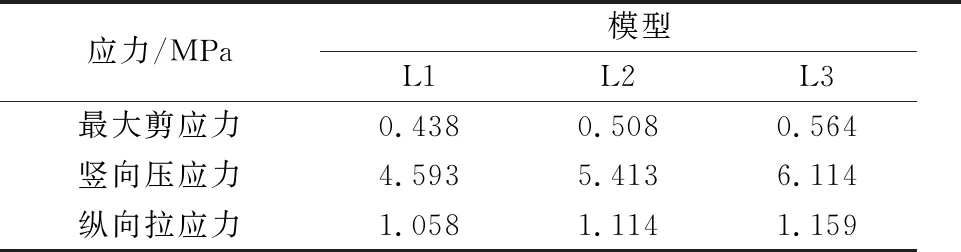
表7 阶梯面应力
由表7可知,三种主要应力都会有所增加:竖向压应力增加幅度最大,为33.1%;其次为最大剪应力,为28.8%;增加幅度最小的为纵向拉应力,为9.6%.
3.2.2阶梯面宽度影响性分析
选择L1型连接形式为有限元模拟的形式,设置五种模型的阶梯面宽度分别为100,150,200,250和300 mm,分别命名为L100,L150,L200,L250,L300型.
1) 连接接缝处应力分析 通过对五种模型的应力云图与应力数据分析,得知五种连接方式对装配式T梁的连接处受力性能有较大的影响.具体分析结果见表8.
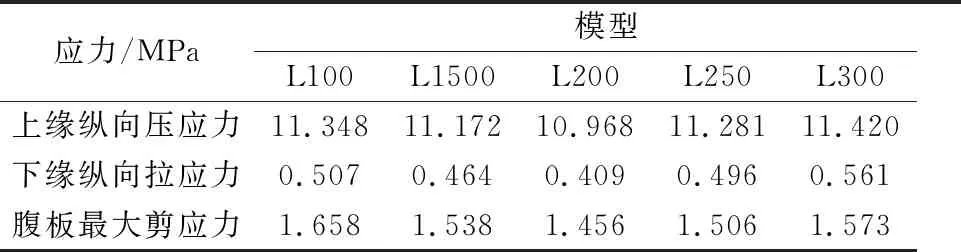
表8 连接接缝处应力
由表8可知,随着阶梯面宽度的增加,三种主要应力均呈现先减小后增加的趋势,尤其以下缘纵向拉应力与腹板剪应力的增减幅度最为明显,上缘纵向压应力数据变化幅度较小.
2) 阶梯面应力分析 对五种模型应力云图与应力数据分析,得知五种连接方式对装配式T梁的连接处阶梯面的受力性能有较大的影响,具体结果见表9.
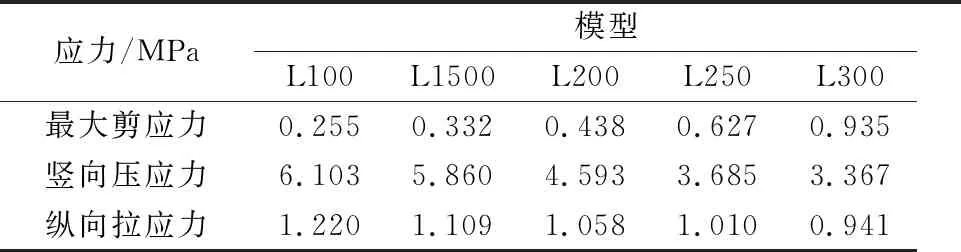
表9 阶梯面应力
由表9可知,随着阶梯面宽度的增加,延阶梯面方向的最大剪应力会有明显的增加,最大值约为最小值的4倍;竖向压应力的变化也较大,最大值约为最小值的2倍.
3.2.3L形或阶梯形接缝影响因素分析总结
通过实际情况与模型的分析得知,阶梯面这种特殊构造承担了原本接缝承担的剪应力与大部分的竖向与纵向正应力. 在施工条件允许与实际情况良好的情况下,L2型即双阶梯形为较优选择;但一般来说,为了防止连接处出现拉应力破坏与简易施工,L1型为较优选择.
在阶梯面宽度较小时,阶梯面不能够承担连接处的所有应力,其抗剪性能未能充分发挥其作用,因此其剪应力值较小.
综上所述,L200型即阶梯面宽度为200 mm的L形接缝连接形式,为改善装配式T梁的受力性能较优的选择.
3.3 齿块型接缝影响因素分析
根据之前相关研究表明,齿键的倾斜角度应与混凝土剪切破坏裂缝(与水平面为45°夹角)一致,齿键构造见图8.
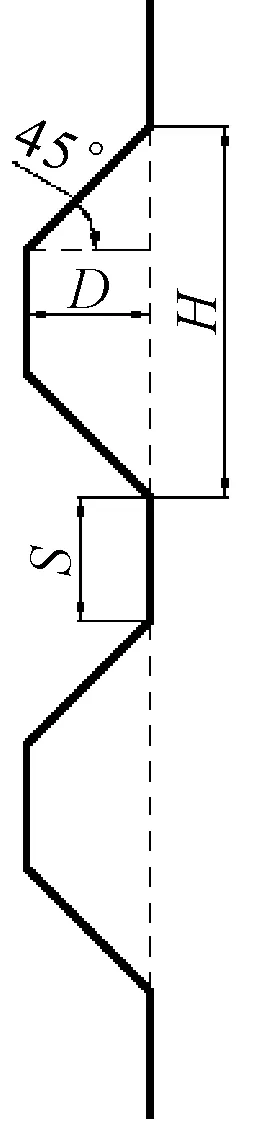
图8 齿键构造示意图
根据实际工程要求与有限元模型模拟需求,选择深度为70,75和80 mm的齿键,分别将其命名为D70、D75与D80型.为了对比不同齿键间距的性能,选取D70与D75型,改变其间距大小,分别使间距S为1/2、1与3/2的齿键深度进行有限元模拟对比分析.不同的齿块形接缝连接类型见表10.

表10 模型编号
通过对七种模型的分析得知,其竖向最大变形与跨中截面应力无明显差别,因此,下面将对连接处应力与齿键应力进行重点分析.其应力云图见图9.
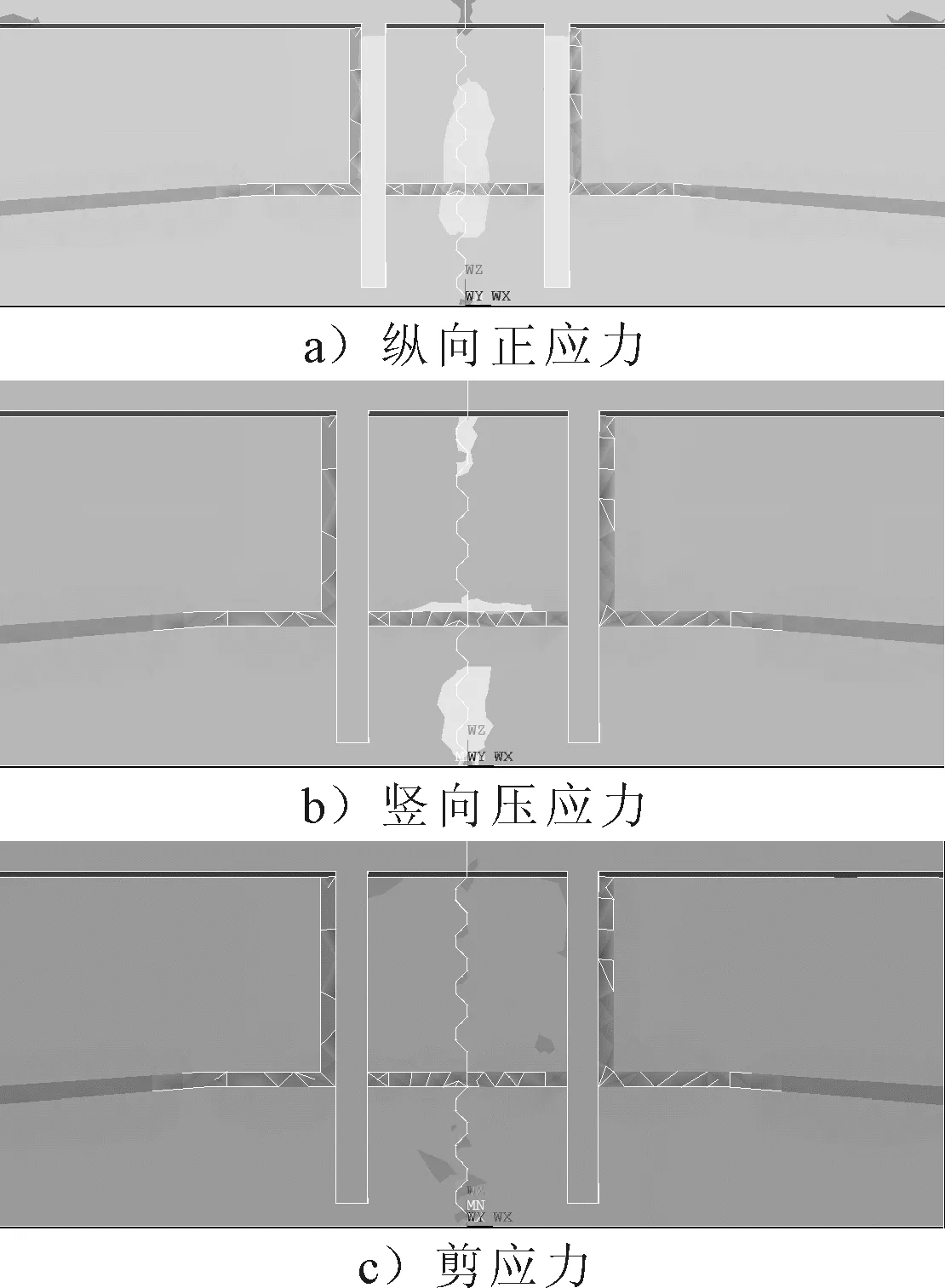
图9 齿块形接缝应力云图
3.3.1齿键深度影响性分析
选择齿键间距都为S=D的D70-1、D75-1与D80-1三种模型进行对比计算分析,并且将其齿键编号按从上缘至下缘分别编号为α1~α7.
1) 连接接缝处应力分析 通过对三种模型的应力云图与应力数据分析,得知三种连接方式对装配式T梁的连接处受力性能有一定的影响.具体分析结果见表11;为了显示其各种应力的增减幅度与比例,使D70-1型为类比项,其余两种为对比项(以下相同).
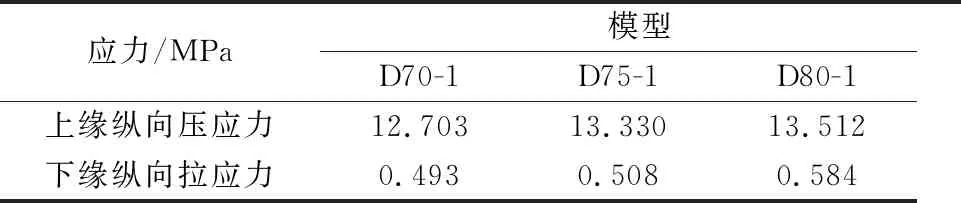
表11 连接接缝处应力
由表11可见,改变齿键的深度对装配式T梁的连接处的上、下缘应力影响较小,但纵向正应力都呈现增加的趋势.
2) 齿键应力分析 对三种有限元模型的七个齿键的应力数据进行分析,将上缘至下缘的齿键应力绘制成图10.
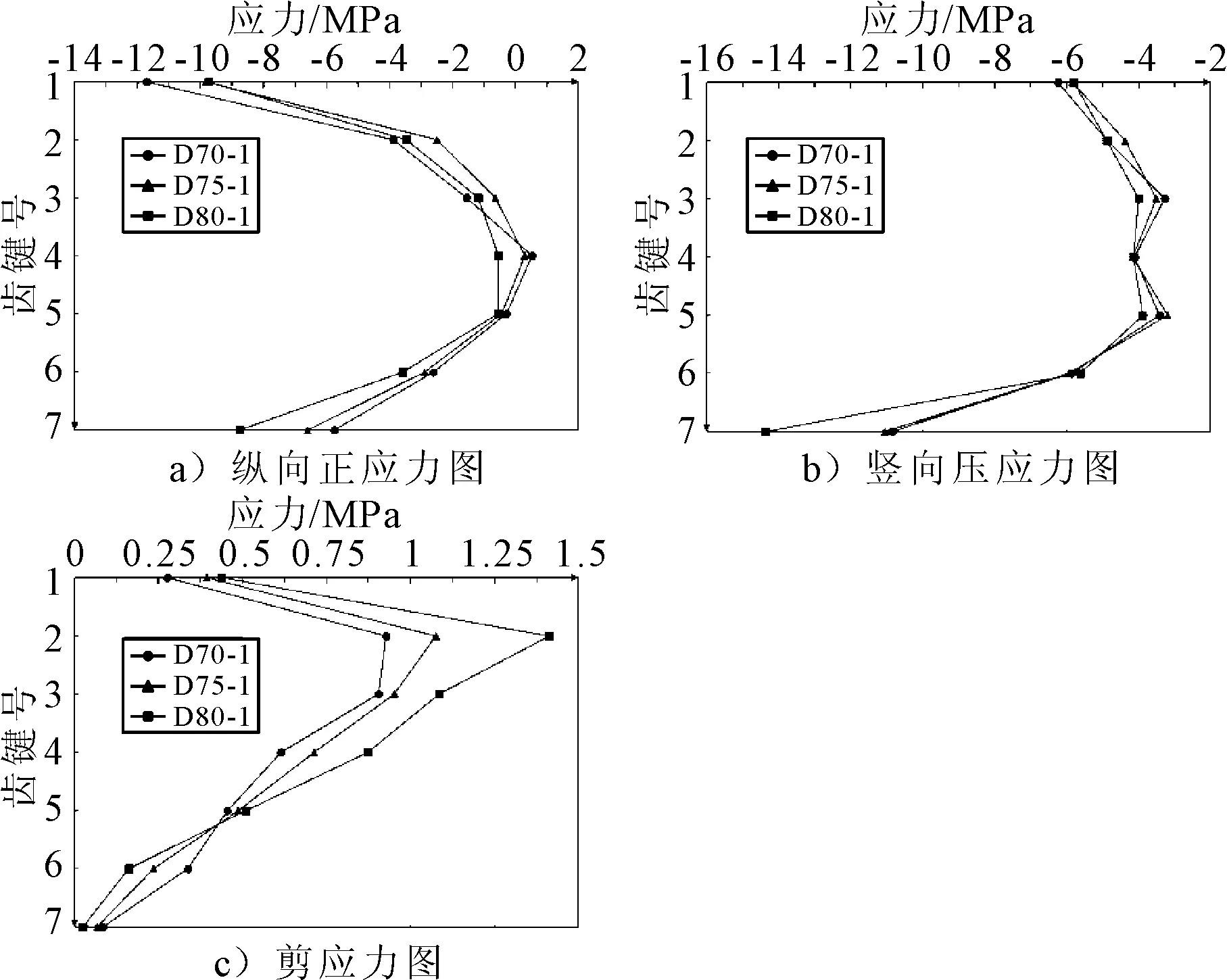
图10 齿键应力图
由图10可知:不同的齿键深度对于齿键的受力性能是有明显的影响.由齿键应力图所示,在纵向与竖向应力图中,α1与α7应力变化最明显;剪应力图中极大值变化最为明显,使其对比结果明显,见图11~12.
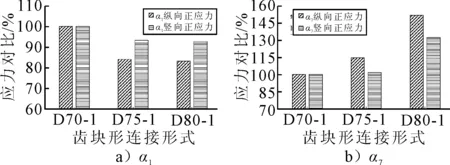
图11 齿键α1与α7应力对比图
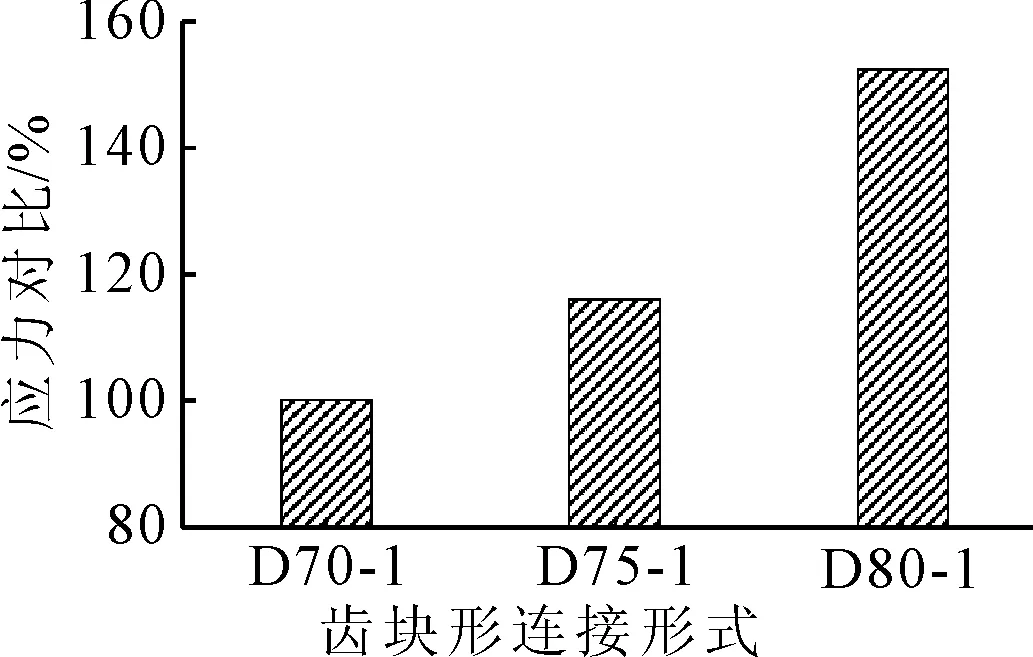
图12 齿键最大剪应力对比图
由图11a)可知,靠近上缘的α1应力最大,在α4处应力值最小,对实际模型的变形分析可知,此处为腹板受拉区域;但在齿键深度D大于80 mm时,腹板受拉区会消失.由图11b)可知,靠近下缘的α7应力最大,在α4处应力出现突变,此处为T梁腹板截面变形处,变化处易出现应力集中.由图11c)可知,上缘附近齿键α1应力随着齿键深度增加而减小;下缘附近的齿键α7应力随着齿键深度增加而增大,并且变化较大.随着齿键深度的增加,齿键的最大剪应力增加幅度较为明显,极值之间的差距为50%.
3.3.2齿键间距影响性分析
选择具有相同齿键数量的D70-1/2、D70-1、D70-3/2与D75-1/2、D75-1、D75-3/2两组有限元模型进行对比计算分析.
1) 连接接缝处应力分析 通过对D70与D75两组六种模型的主应力云图与应力数据分析,得知六种连接方式对装配式T梁的连接处受力性能有一定的影响.具体分析结果见表12.
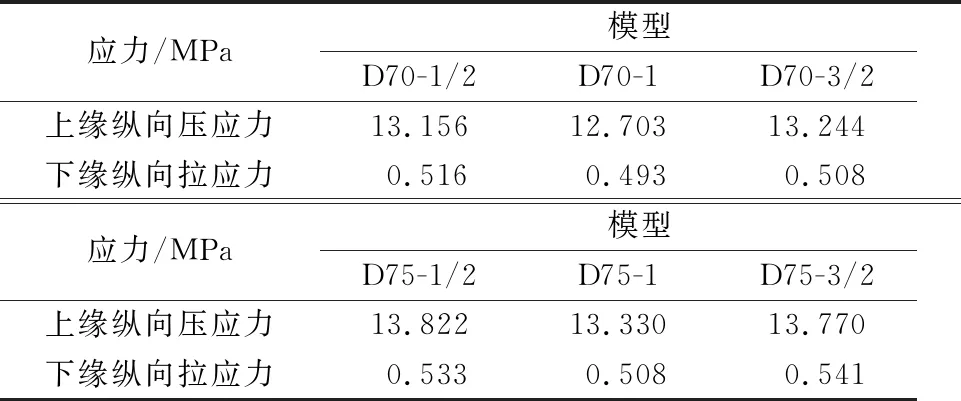
表12 连接接缝处应力
由表12可知,改变齿键间距对于连接处的应力影响较小,D70型应力变化在3%~5%之间;D75型应力变化在4%~6%之间.但是,无论是增加齿键间距还是减小齿键间距,其上下缘的应力都会有一定值的增加,因此,需要通过结合其他细部构造共同分析.
2) 齿键应力分析 通过对六种有限元模型的分析计算,从计算结果中筛选并汇总七个齿键的应力数据,将上缘至下缘的齿键应力见图13~15.
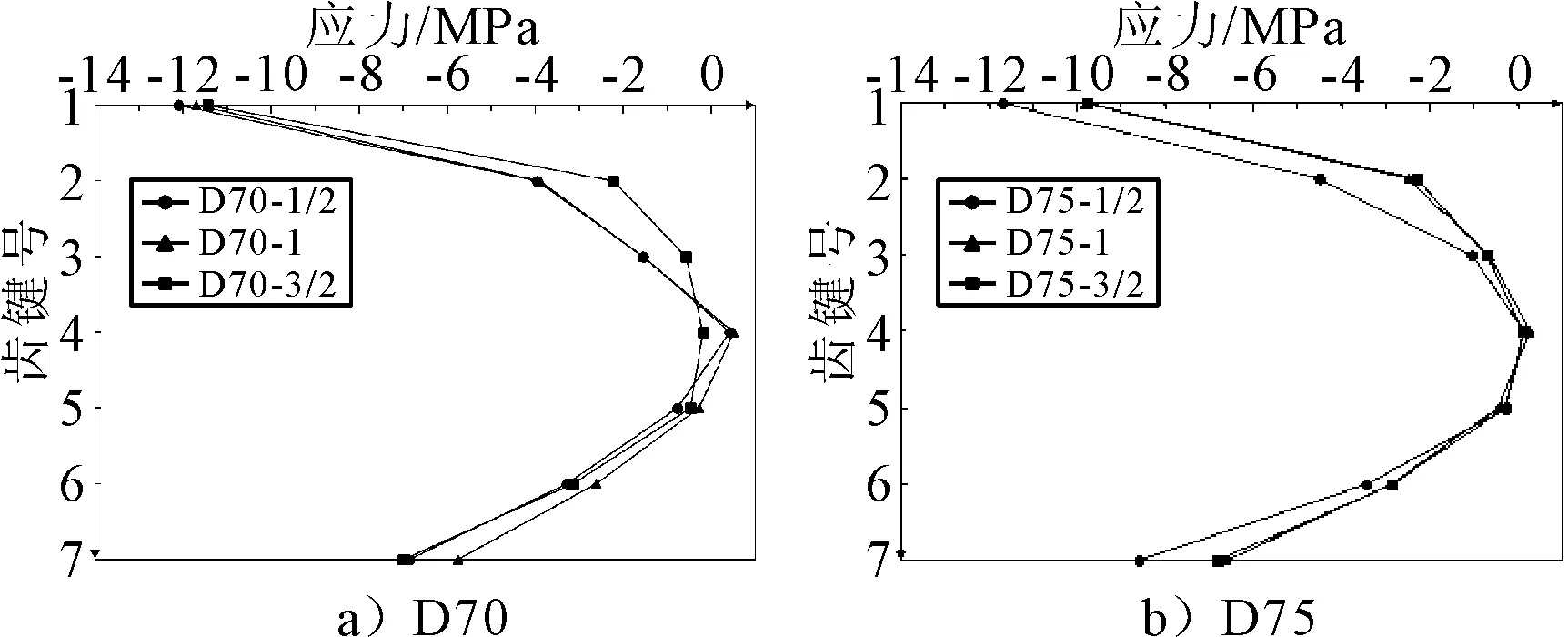
图13 纵向正应力
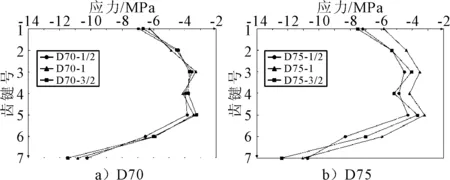
图14 竖向压应力
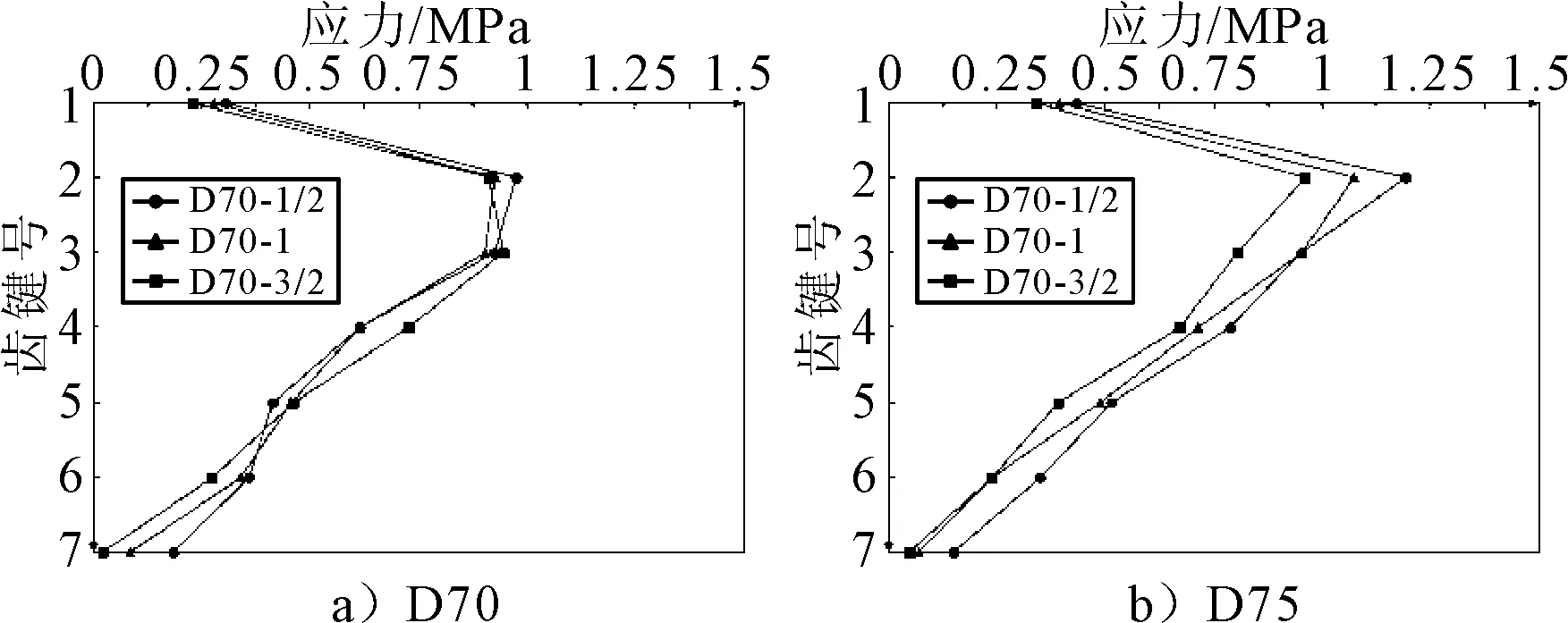
图15 剪应力
六种模型的齿键应力图与上以节相似,根据上一节的分析内容,将S-1/2为类比项,其他两项为对比项,做对比图见图16~18.
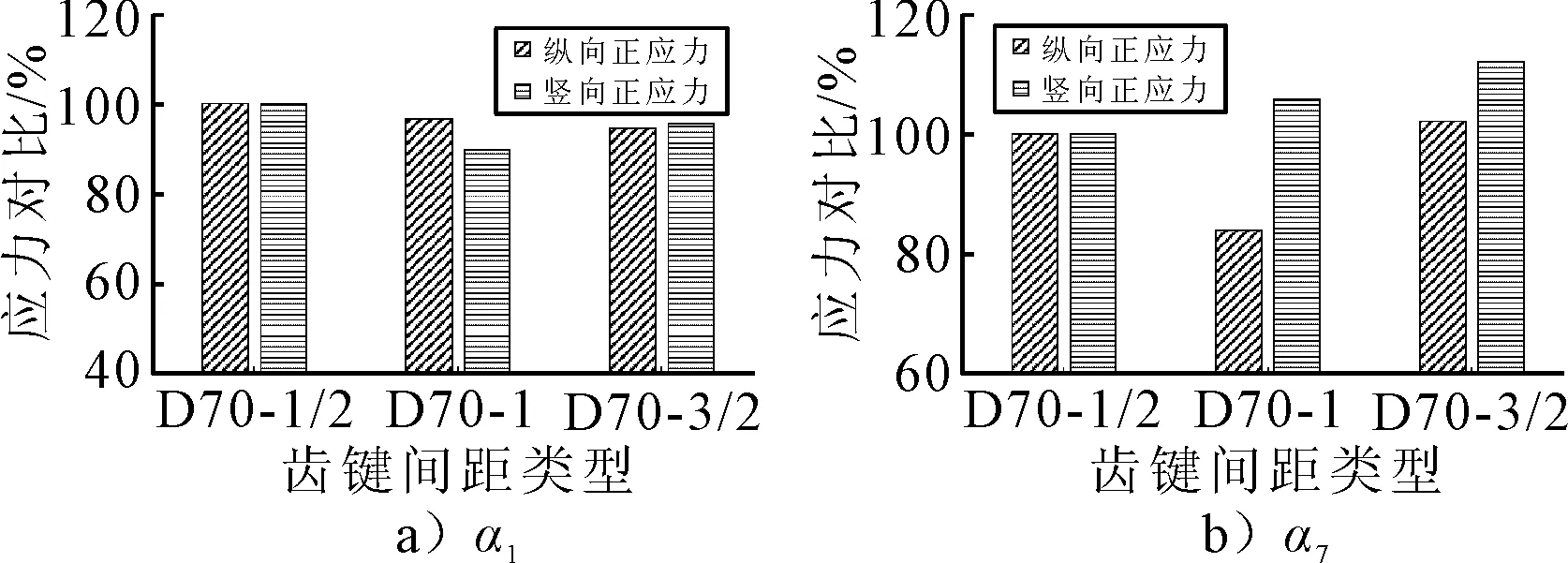
图16 D70型齿键α1与α7应力对比图
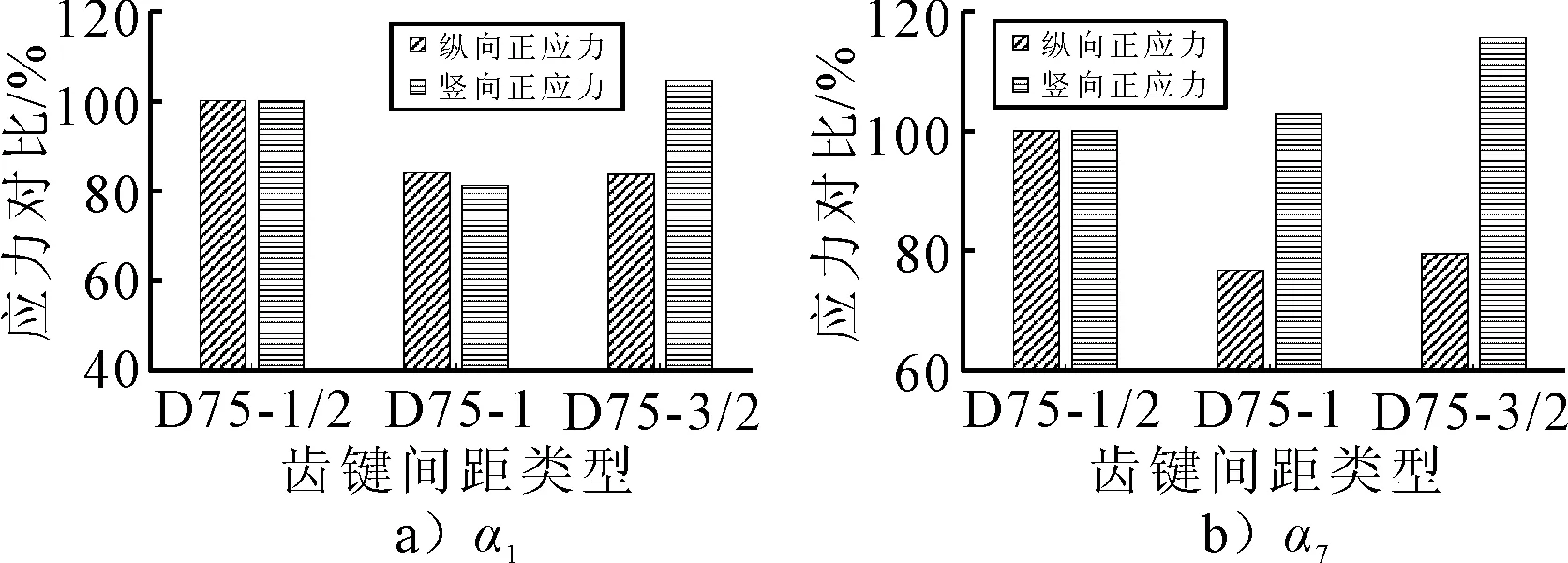
图17 D75型齿键α1与α7应力对比图
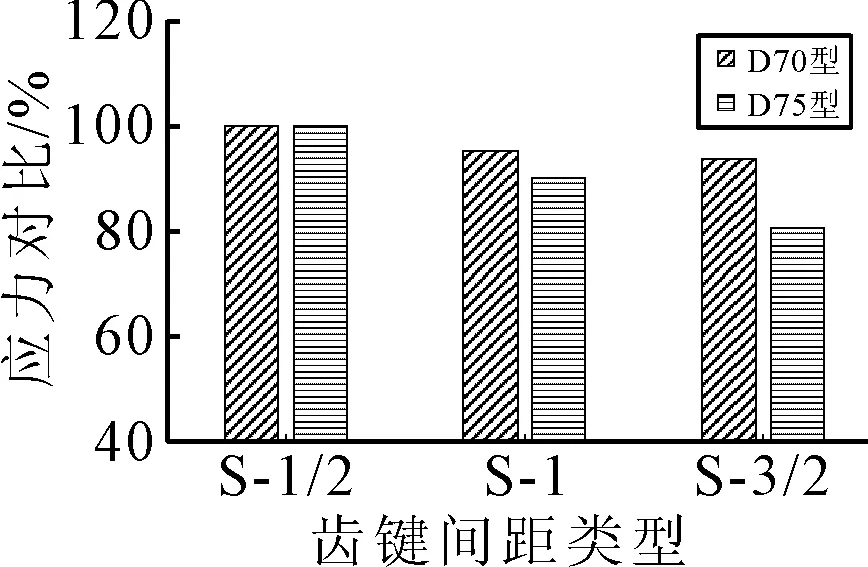
图18 齿键最大剪应力对比图
由图16可知:α1的应力随着齿键间距的增加而减小,但减小幅度较小;下缘附近的齿键α7应力变化最为明显,且都呈现S-1型的应力较小.由图17可知:α1的应力变化较为明显,都呈现S-1型应力较小;α7应力随着齿键间距的增加而增加,但增加幅度相比α1的变化幅度较小.由图18可知:两种类型的接缝的最大剪应力都呈现随着齿键间距增大而减小的趋势,并且D75型相比D70型的变化幅度较大.
3.3.3齿块形接缝影响因素分析总结
1) 齿键深度的增加使得连接处上、下缘应力与最大剪应力都有一定值的增加,齿键的应力在下缘附近也显著增加,但齿键深度较小不能解决腹板受拉区域的问题,因此选择75 mm型齿键.
2) 改变齿键间距,当间距S等于深度D时,连接处上下缘的应力最小.其主要原因为,改变齿键间距,使得阴阳面的齿键形状不一致,导致其受力变形有一定的差别.
3) 齿键间距的增加,使得齿键的最大剪应力有一定值的减小,D70型减小幅度约为3%,D75型减小幅度约为10%.较小的齿键间距,使得齿键较为密集,局部会有应力集中问题,但有利于承担T形截面中性轴处的最大剪应力.
综上所述,对于此装配式T梁,一般来说,齿键间距等于齿键深度的构造对于改善装配式T梁的受力性能为最佳的选择;也可根据实际工程情况进行适当改变,但应该使S/D在1与3/2之间变化.
4 结 论
1) 随着倾斜角度的增加,其连接细部的主要应力都有所较小,但局部变形会变大,所以在考虑施工难度与安全性原因,15°的倾斜角度为较优选择.
2) 随着阶梯面数量的增加,剪应力会减小但拉应力有一定的增加;阶梯面宽度的过小,使得阶梯面不能完全发挥其作用,而过宽会使重要应力增加;所以选择单阶梯面200 mm宽度的L形接缝为较优选择.
3) 齿键深度的过小无法解决腹板附近产生的拉应力问题,而过大使得下缘应力增加较大;齿键间距过小导致齿键密度增加,应力集中问题严重,而间距过大使得下缘附近齿键应力明显增加;综上考虑,选择齿键间距与深度相等的75 mm深度齿键(厚度为225 mm)类型为较优选择,并且施工种尽量选择齿键间距与深度比为1~3/2的齿键类型.
