压电获能振子的力学建模与参数敏感性分析
2021-07-07徐业鹏
陈 明 徐业鹏 黄 丹
(河海大学力学与材料学院 南京 211100)
0 引 言
波浪能是一种储量丰富的可再生清洁能源[1],但传统的机械式波能发电装置往往存在体积庞大、易腐蚀和依赖地形等问题[2-3],限制了其推广应用.而压电式波能发电基于压电材料的机电转换特性,可以大幅简化装置结构,且具有耐腐蚀、强度高和成本低等优良特性,适合在海洋环境中工作,因而极具潜力[4-5].
压电振子是压电获能领域中应用最广的一种基本发电单元,一般由压电薄膜和基板复合而成,其结构简单、体积小,适用于各种复杂工况.近年来,针对各种类型压电振子发电的相关研究[6-7]越来越多,并取得系列成果.Wang等[8]设计了一种高灵敏度的多层垂直蝶形压电发电装置,可用于道路预警标识的供电;宁艺文等[9]设计了一种PVDF压电悬臂梁发电装置,可以有效收集一定风速范围内的风能发电;郭磊[10]设计了一种克服振源不稳定问题的多压电振子阵列式宽频振动能量采集器.然而,已有研究更多关注于新型压电获能装置的设计,而对获能机理与建模相关的研究相对较少.Vinayaga等[11]曾研究了压电振子的电能输出与参数的关系;Lee[12]提出一种压电层合板理论,推导了悬臂梁式压电层合板表面电荷与中性面上各点位移的关系,Wu等[13]基于该理论设计出一种兼具有较高获能效率和较低机械传动能量损失的小型浮标式压电获能装置.压电振子获能相关的机理性研究通常受限于各种理想假设,例如规则形状与规律激励,对于形状不规则压电振子、非规律性外部激励作用下的压电获能机理研究较少.
文中基于力电耦合方程构建了规则形状压电振子表面电荷的连续求解模型,并结合有限元思想构建压电振子形状不规则情况下的离散求解模型,研究压电振子的发电机理.在验证模型求解精度的基础上,分析了各关键参数对振子发电效率的影响.
1 模型与方法
1.1 基本方程
弹性压电材料具有介电性和弹性两种性质,因此压电方程是耦合方程,为
(1)
式中:T为应力;S为应变;D为电位移;E为电场强度;cE为弹性矩阵;e为压电常数矩阵;ε为介电常量矩阵.
压电方程根据其力学与电学边界条件可分为四类,式(1)是第二类压电方程,其适用于机械夹持和电学短路的边界条件[14].
1.2 连续模型
图1为压电获能装置示意图,其中振子与拨片视为铰接,以广泛使用的矩形截面悬臂梁式压电振子为例(上表面贴有z方向极化的压电片),压电振子简图见图2.

图1 压电获能装置示意图

图2 压电悬臂梁简图
根据高斯定理可得压电材料表面电荷为
(2)
假设中性面位移为u0(x方向),v0(y方向),w=w(x,y,t)(z方向),悬臂梁厚度为h,上表面压电片区域为Ω,无外电场(E1=E2=E3=0),则压电片表面电荷为
q(t)=
(3)
根据实际情况,若忽略悬臂梁的水平位移,则电荷表达式可简化为
(4)
式(4)即为压电振子表面电荷与中性面位移的关系.
当压电振子厚度不是恒定值时,式(4)可变为
(5)
1.3 离散模型
电位移的积分面为压电振子上表面,故可建立位于x-y平面的求解电荷的二维离散模型.本离散模型基于有限单元法思想,采用四边形八结点等参单元进行离散,单元的局部编号和单元在积分面的分布见图3.

图3 单元局部编号及积分面
作为标量,电荷可写为求和形式
(6)
式中:i为单元编号;qi(t)为每个单元的电荷量.
每个单元上的电荷量为
(7)
式中:Ωi为单元区域.
转化为局部坐标下的表达式
(8)
(9)
式中:Hm,Hn为积分权重;ξm,ηn为高斯积分点.
采用等参单元,位移模式与坐标变换具有相同的形函数N={Nj},由此可得整体坐标与局部坐标的关系、位移与局部坐标的关系
(10)
式中:xj,yj为结点的平面坐标.
(11)
式中:wj为结点的z方向位移.根据式(11)易知本模型只能采用高次等参单元.
1.4 电流的近似求解
由压电振子的离散模型可以近似求得每个单元上的电荷量,通过电荷叠加即可得到每一时刻压电振子表面的电荷总量.
假设每个时间节点tk=t0+kr(k=0,1,2…n)上的电荷量为q(tk),不考虑能量损失,则电流可用三点数值求导公式求得
式中:t0为初始时刻;r为时间步长.
2 模型验证
2.1 验证算例

中性面位移由梁的挠曲线计算求得.其与坐标关系满足
(13)
(14)

图4 压电振子尺寸及挠度曲线
2.2 精度验证
理论解通过压电层合理论计算得到,数值解由本文离散模型计算得到,两组解的对比见表1.由表1可知,本文模型计算结果具有较高的精度,相对误差在0.5%以内.

表1 计算结果比较
在求得压电振子的电荷变化规律后,根据上文的电流近似求法,可以得到压电振子各个时刻的电流值及电流输出曲线,见表2和图5.由图5可知:数值解与理论解吻合良好,且电流都与时间呈余弦关系,波浪波峰波谷处由于电荷变化率低,电流约为零,而半周期时刻液面变化速度最快,因此电流达到最大值.

表2 各个时刻的电流值

图5 周期性电流输出
2.3 电荷分布分析
除电荷总量和电流时间曲线外,还可以得到一个周期内压电振子上表面的电荷变化规律,波浪处于波谷及波峰时的云图见图6.

图6 压电振子的电荷分布
波谷时刻,上表面受到拉伸,压电振子上表面主要分布的是负电荷,固定端的电荷量最为密集,向自由端逐渐稀疏并趋近于零.
波峰时刻,自由端位移达到最大值,上表面受到挤压,同样地,固定端由于弯矩和应变最大,产生了密集的正电荷,沿x正方向电荷逐渐稀疏,直至趋近于零.根据模拟结果分析,由于波浪在短时间内近似看为简谐波,故波峰波谷对压电振子的影响仅为产生的电荷正负不同,而绝对数值无差异,与理论解吻合.
压电振子的设计通常需要考虑材料利用率及成本,压电振子的自由端附件电荷量几乎为零,故可考虑不设置压电片,可参考模拟结果选取电荷的收集范围,既保证发电效率又节省材料.
3 参数分析
3.1 等截面压电振子
图7为电流峰值与压电振子长度的关系曲线.由图7可知,电流峰值随压电振子的长度增加而增加,且曲线斜率增加,主要是由于长度增加后固定端弯矩增加,压电片应变及面积均增大,产生的电荷量显著增多.当限制了发电装置的大小及内部空间后,应尽量增加压电振子的长度以增加装置的发电效率.
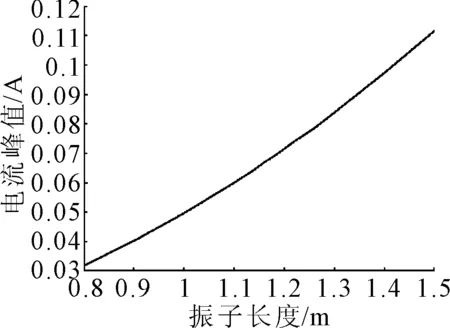
图7 电流峰值与长度的关系
电流峰值与振子厚度的关系见图8.由图8可知,电流峰值随压电振子的厚度增加而减小,这主要是由于厚度增加后,振子的抗弯刚度增大,在同等大小的力作用下,振子的竖向位移减小,应变减小.故在不影响强度的基础上应尽量减小其厚度.
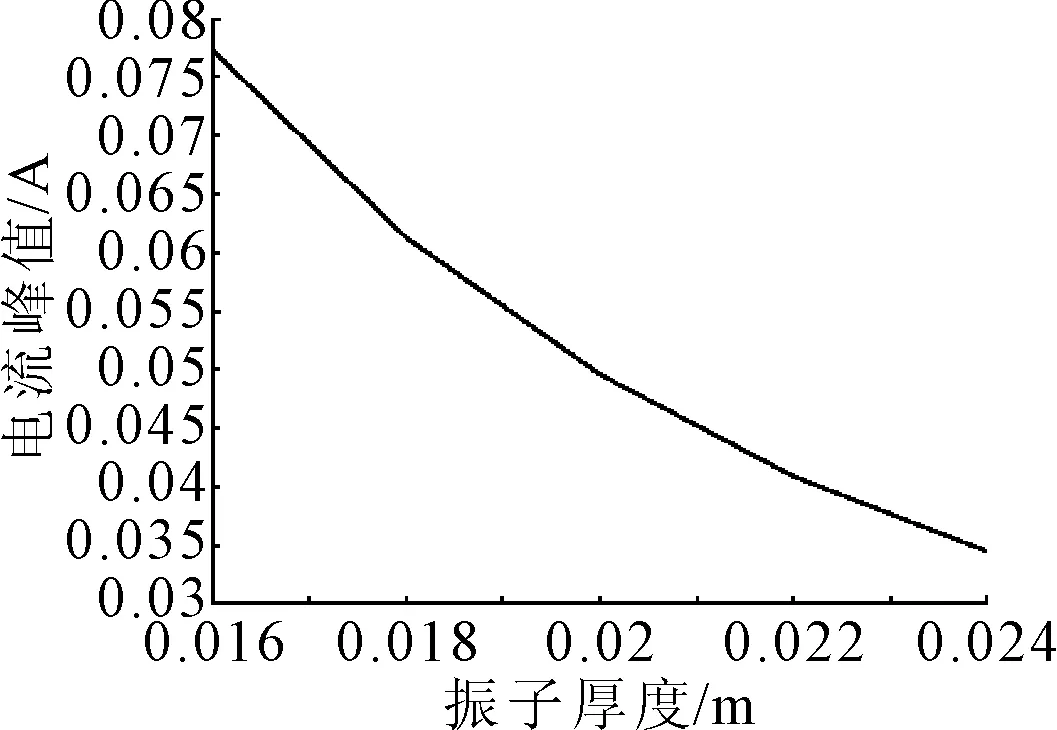
图8 电流峰值与厚度的关系
图9为电流峰值与波浪频率的关系曲线.由图9可知,电流峰值随波浪频率的增加而线性增加,这是由于仅改变频率时,压电振子上表面产生的电荷量是不变的,频率增加即增大电荷的时间变化率.故压电发电装置在波浪频率高处发电效率明显提高.

图9 电流峰值与波浪频率的关系
图10为电流峰值与振子宽度的关系曲线.由图10可见,电流峰值随压电振子宽度的增加而线性增加.该曲线表明振子在单位宽度的发电效率是恒定的,增加宽度与增加振子的数量具有同样的效果.在本文的计算中,波浪力与宽度呈线性关系,故宽度增加不会改变挠度,即电荷密度不随宽度变化,总面积增加,电荷总量增加,输出电流增加.

图10 电流峰值与宽度的关系
3.2 变截面压电振子
相比等截面压电振子,变截面压电振子在同等激励下具有更大的位移,同时也具有更高的材料利用率.变截面压电振子简图见图11.
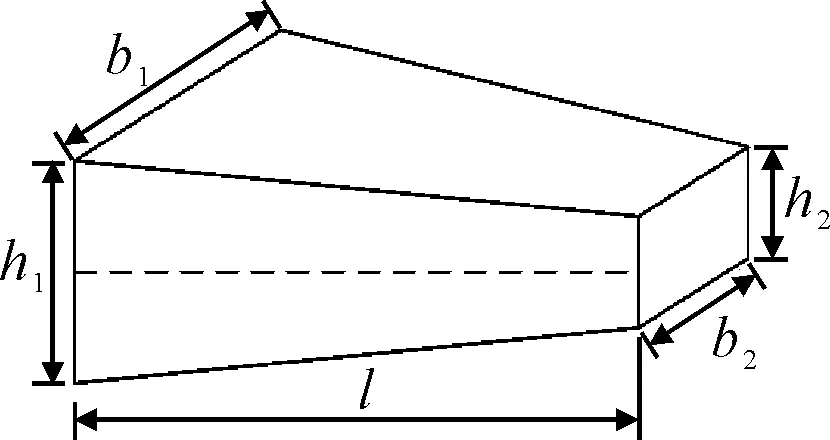
图11 变截面振子简图
基于本文构建的离散模型,采用与2.1相同的材料参数与外荷载(波浪周期取5s),研究变截面压电振子自由端厚度和宽度对电流峰值大小的影响,结果见表3~4.

表3 电流峰值随宽度的变化

表4 电流峰值随厚度的变化
由表3可知:电流峰值随自由端宽度变化无明显变化,其值在0.049 A上下波动.随着振子自由端宽度的减小,其抗弯刚度也随之减小,在同样大小的激励下,振子的挠度及上表面应变增大,压电效应显著增强.同时,当振子自由端宽度减小时,上表面面积减小,此时电位移积分面减小,收集的电荷减少.在上述两种因素的影响下,产生的电荷、电流整体呈稳定趋势.
由表4可知:在宽度一定的情况下,自由端厚度越小,输出电流的峰值越高.虽然厚度影响振子表面的应变,但厚度对抗弯刚度的影响更大,该变化规律与3.1的结论一致.
图12为三种变截面振子的输出电流峰值与自由端厚度的关系,三种振子的几何参数见表5.由图12可知,B振子的自由端厚度即使减小至0.01 m,其输出电流峰值仍低于自由端厚度不变的A振子,所以在保证强度的情况下,固定端越薄越有利于获能,也越节省材料.A、C两种振子自由端宽度不同,但电流峰值曲线贴合良好,表明对于变厚度振子,宽度的影响仍然可以忽略.

表5 压电振子的几何参数 单位:m

图12 电流峰值与自由端厚度关系
4 结 论
1) 本文构建的求解压电振子表面电荷的模型可以实现波浪作用下压电振子的电荷电流高精度求解.
2) 广泛使用的悬臂式压电振子在波浪荷载作用下,越接近固定端电荷密度越高,自由端约为零.压电振子在液面处于波峰波谷时的输出电流为零,在水平高度时输出电流最高,在一周期内近似为交流电.
3) 等截面压电振子的电流峰值随振子长度增加而增大,随厚度增加而减小,与振子宽度和波浪频率变化呈线性关系.
4) 变截面压电振子的电流峰值随自由端厚度的减小而增大,随自由端宽度的减小无明显变化.
