考虑级差贡献的航道PPP项目投融资决策方法
2021-07-07符雪剑周红梅石圣雅
符雪剑 周红梅 肖 浩 石圣雅
(武汉理工大学交通学院 武汉 430063)
0 引 言
近年来,公私合作模式(public-private-partnership,PPP)在我国交通基础设施建设领域发挥了重要作用.与公路、铁路、机场等交通基础设施相比,航道投资主体单一、投资效率不高、融资困难,国内外通常的融资办法是以政府投资为主,多渠道筹集资金,对于许多地方政府财政难以负担的航道项目采用PPP模式建设成为一种有效可行的路径.文中考虑不同类型航道对区域经济贡献和影响不同由大到小可分为高等级航道,地方重要航道和地方一般航道,且水运基础设施建设属于不可逆投资项目,其不确定性高、投资额度巨大、盈利性不明显.因此,在PPP项目投融资模式决策过程中必须要考虑航道项目的级差贡献,从项目的等级属性和自身真实价值出发,减少决策的主观偏好和外界环境的影响,选出最佳的投融资模式.
PPP项目是近年研究的热点,但对于PPP项目投融资模式决策研究不多.Schaufelberger等[1]对亚洲、北美的若干PPP项目实际案例进行分析,提出PPP项目的自身属性、投融资渠道、风险在PPP模式选择中起关键作用.Khalil[2]先构建了PPP模式的决策指标体系,再通过运用层次分析法对PPP模式进行选择.杨卫华等[3]构建出PPP模式的三级分类结构,在所有权转移效益、经营权控制程度、公私合作程度的三维框架内,结合公共项目的自身属性找出PPP模式选择的路径.Zhang等[4]提出项目成本、VFM效果、进度和产品是选择PPP模式的标准.
物有所值(VFM)是国际通行的PPP项目评估标准,VFM评价是PPP项目前期决策的核心.我国的VFM评价的应用与实践仍处于不断探索的过程中,刘雪婷等[5]专门构建了针对城市地下综合管廊PPP项目物有所值定量评价模型.张家诚[6]考虑不确定性,将传统PPP项目VFM评价确定性点决策推向分布式区间决策.潘鹏程等[7]将直觉模糊集引入VFM评价中,建立了考虑社会效益基于直觉模糊集的物有所值评价决策模型.值得注意的是,目前研究PPP模式决策的影响因素或标准,都是从具体项目的自身属性出发,运用定性或定量单一方面论述其合理性.
鉴于水运基础设施(港口、航道工程)投融资的特殊性,文中经梳理相关文献并结合财政部《PPP物有所值评价指引》,构建了考虑极差贡献的航道PPP项目评价指标体系,引入区间直觉模糊集定量决策中的满意度、不满意度、犹豫度,为解决主观经验确定指标权重带来评价结果失真的不足,运用前景理论精确得出评价指标全局最优权重值,以得分函数与精确函数的得分进行排序,形成一套更加贴近实际的决策方法.
1 区间直觉模糊数与前景理论相关定义
1.1 区间直觉模糊集理论相关概念
1.1.1区间直觉模糊集的概念
设X是一个非空集合,则称
A={(〈x,μA(x)〉,νA(x))/(x∈X)}
(1)
为直觉模糊集,其中μA(x)和νA(x)分别为X中元素x属于A的隶属度μA:X→[0,1]和非隶属度νF:X→「0,1⎤,且满足条件0≤μA(x)+νA(x)≤1,∀x∈X.此外,1-μA(x)-νA(x)表示X中元素x属于X的犹豫度.
Atanassov[8]将Zadeh的模糊集进行了推广,给出了区间直觉模糊集的概念.A={〈〈x,μA(x)〉,νA(x)〉│x∈X}为区间直觉模糊集,其中μA(x)⊂[0,1],νA(x)⊂[0,1],且满足条件max(μA(x)+νA(x))≤1,∀x∈A.
1.1.2区间直觉模糊数与运算法则
由X中元素x构成区间直觉模糊集的基本组成部分中隶属度与非隶属度所组成的有序区间对称为直觉模糊数.一般将其形式简记为([a,b],[c,d]),其中:[a,b]⊂[0,1],[c,d]⊂[0,1],b+d≤1,∀x∈X.
运算法则[9]设α1=([a1,b1],[c1,d1])和α2=([a2,b2],[c2,d2])为任意两个区间直觉模糊数,可得如下运算法则
距离公式[10]设α1=([a1,b1],[c1,d1])和α2=([a2,b2],[c2,d2])为任意两个区间直觉模糊数,则
|c1-c2|+|d1-d2|)
(3)
为区间直觉模糊数α1与α2之间的距离.
1.1.3区间直觉模糊数的集成算子[11]
设αj=(μ(Aj),ν(Aj))(j=1,2,3,…,n)为一组区间直觉模糊数,且设IFWG:Θn→Θ(为全体直觉模糊数的集合Θ),若
(4)

1.1.4区间直觉模糊数的比较方法
运用区间直觉模糊数的得分函数与精确函数来比较α1和α2的大小.
区间直觉模糊数的得分函数可以较好地反应直觉模糊数的大小,设α=([a,b],[c,d])为区间直觉模糊数.则得分函数[12]:
(5)
式中:δ(α)∈[-1,1],显然,δ(α)越大,则α越大.当δ(α)=1,α取最大值([1,1],[0,0]);δ(α)=-1,α取最小值([0,0],[1,1]).
特殊情况下,若取α1=([0.4,0.5],[0.4,0.5]),α2=([0.2,0.3],[0.2,0.3]),则δ(α1)=δ(α2)=0,得分函数无法对α1和α2进行比较,为解决这类特殊情况,下面给出一种精确函数:
设α=([a,b],[c,d])为一个区间直觉模糊数,则精确函数:
(6)
式中:η(α)∈[0,1],η(α1)和η(α2)分别为α1和α2的精确度.特殊情况下,当δ(α1)=δ(α2),则
1) 当η(α1)<η(α2),规定α1小于α2,记为α1<α2.
2) 当η(α1)=η(α2),规定α1等于α2,记为α1=α2.
1.2 前景理论相关概念
前景理论(prospect theory)[13]在考虑决策者心理和行为的基础上,用前景价值作为决策依据,前景价值W是由价值函数与权重函数共同构成,即
(7)
式中:ψ(p)为权重函数;p为产生概率,其表达式为
(8)
价值函数υ(Δx)以结果的实际价值为自变量,其幂函数表达式为
(9)
式中:λ为参考点;α,β,θ为风险系数,α,β分别为风险偏好和风险厌恶程度;θ为风险规避系数(一般认为θ>1);Δx为xi到参考点λ的距离;价值函数表现出特征有:收益与损失不是绝对概念,是相对参考点而言,当决策者面对正向收益时通常表现为风险规避,面对损失时风险偏好;决策者对损失比收益的心理波动更大.
2 考虑级差贡献的航道PPP项目投融资方案决策方法
2.1 问题描述
在实际的航道PPP项目投融资过程中,不同等级的航道项目,往往面临多套投融资方案的选择.高等级航道项目考虑更多的是项目社会公益性贡献,而投资收益偏低,而地方重要航道或一般航道,则考虑更多的是风险识别、投资收益与可融资性,航道等级属性不同就决定了对投融资方案决策的差异性.VFM是国际通行的PPP项目评估标准,在构建评价指标体系过程中,要考虑航道项目的特殊性来制定相应的二级评价指标,且根据航道等级不同确定指标权重范围.将前景理论引入到区间型多属性决策中来,解决属性权重信息不完全、决策者对各投融资方案存在一定的主观偏好的问题.引入区间直觉模糊集解决专家评估过程中的满意度、不满意度和犹豫度的问题,利用区间直觉模糊集的集成算子,得到决策矩阵中相应于各方案的综合区间直觉模糊值,通过区间直觉模糊数的排序方法,选出相对最佳融资方案.
2.2 决策途径
2.2.1航道PPP项目评价指标体系构建
依据《PPP物有所值评价指引(试行)》的规定,VFM的评价指标分为三大类,包括基本评价指标6项、补充指标和社会公益性评价指标,构建适用于航道项目的二级评价指标体系,并且根据决策成员的专业能力与内在经验确定不同等级航道项目的二级评价指标权重范围(即高等级航道μj1、地方重要航道μj2、地方一般航道μj3),见表1.

表1 航道PPP项目评价指标体系
2.2.2决策者评价信息处理
决策者在熟悉了项目的基本情况、资金测算、可行性实施方案,依据航道PPP项目的评价指标体系对各投融资方案X={x1,x2,…,xm}进行评价.假设有关投融资方案xi在各指标[μ1,μ2,…,μn]下的评估信息经过统计处理可以表示成直觉模糊数αij=([aij,bij],[cij,dij]),即i方案在j指标下的评价得分,则可构成区间直觉模糊矩阵Ak=(αij)m×n.由于在航道PPP项目评价指标体系中仅存在效益型指标,没有成本型指标,则无需对评价信息矩阵规范化处理,即Ak等于规范化矩阵Rk.
2.2.3基于前景理论计算各评价指标的全局最优权重值
根据航道项目的自身等级属性,匹配相应的评价指标权重信息,针对评价的指标权重信息不完全的问题,本文提出一种基于前景理论的权重计算方法,选取两种形式的理想融资方案作为双参考对象.
max[(ai2,bi2),(ci2,di2)],…,
max[(ain,bin),(cin,din)]},i∈m
最不利融资方案:
min[(ai2,bi2),(ci2,di2)],…,
min[(ain,bin),(cin,din)]},i∈m
然后,根据区间直觉模糊集的距离公式即式(3)求得各融资方案xi分别到最佳融资方案与最不利融资方案的距离集.
max[(ai1,bi1),(ci1,di1)]),d([(ai2,bi2),(ci2,di2)],…,
max[(ai2,bi2),(ci2,di2)],…,d([(ain,bin),(cin,din)],
max[(ain,bin),(cin,din)]},i∈m
与
min[(ai1,bi1),(ci1,di1)]),d([(ai2,bi2),(ci2,di2)],…,
min[(ai2,bi2),(ci2,di2)],…,d([(ain,bin),(cin,din)],
min[(ain,bin),(cin,din)]},i∈m
(10)
(11)
由式(10)~(11)可得到方案的正前景矩阵W+与负前景矩阵W-,各方案的综合前景值为正前景值与负前景值之和.
对于各融资方案xi而言,其真实前景值总是越大越好,然而方案的对比只有同一个标准下才能区分出来.因此,假设决策者对每一个投融资方案没有偏好,各方案之间公平竞争,存在一组确定的权重μi=(μ1,μ2,…,μn),使各投融资方案的综合前景值最大,因此可以设定目标函数.
maxW=(W1(x1),W2(x2),…,Wm(xm)) (12)
(13)

2.2.4利用集成算子计算各投融资方案的区间直觉模糊值
利用加权算数平均算子,将评价信息规范化矩阵Rk与指标权重向量μj进行集结:
i=1,2,…,m
(14)
集成决策矩阵D中第i行第j列的所有元素αij(j=1,2,…,n),从而得到方案xi的区间直觉模糊值αi(i=1,2,…,m).
2.2.5利用得分函数与精确函数进行排序
分别利用区间直觉模糊数的得分函数与精确函数计算αi的得分函数值δ(αi)和精确函数值η(αi),进而根据各区间直觉模糊数的得分对方案xi进行排序,从而得到最佳方案.
3 算例分析
在湖南省某地方重要航道工程项目中,拟采用PPP模式,对该项目的具体投融资模式进行评估决策,该航道PPP项目备选投融资模式X={x1,x2,x3,x4},其中x1为船闸收费+民营资本,x2为流域综合开发,x3为特许经营权+民营资本,x4为其他(银行贷款、发行债卷).其中流域综合开发,包括砂石特许经营、沿线土地租赁等.该航道PPP项目的评价指标体系与各指标权重范围μj2见表1,可视化后见图1.

图1 地方重要航道PPP项目的评价指标与各指标的权重范围
具体决策程序如下:
步骤1将该航道PPP项目的4种投融资模式(x1、x2、x3、x4)在各评价指标下的决策信息经过统计处理后,可表示为区间直觉模糊数,进而构成评价得分信息矩阵.该项目的评价指标体系的10个指标均属于效益型指标,本案例中社会公益型指标也为正,因此不需要将评价信息矩阵规范化操作,即Ak=Rk,见表2.

表2 决策者评价得分信息矩阵Ak=Rk=(αij)n×m
步骤2确定两种形式的参考点
由式(5)~(6)对4种融资模式在各评价指标下的评估信息得分进行比较,确定最佳理想融资方案(参考点一)与最不利理想融资方案方案(参考点二)的得分信息.结果见表3.

表3 两种形式的理想融资方案得分信息
步骤3由式(3)求得各融资方案xi分别到最佳融资方案与最不利融资方案的距离集.
max[(ai1,bi1),(ci1,di1)]),d([(a12,b12),(c12,d12)],…,
max[(ai2,bi2),(ci2,di2)],…,d([(a1n,b1n),(c1n,d1n)],
max[(ain,bin),(cin,din)]}=
(0.320,0.354,0.605,0.398,0.205,
0.517,0.214,0.409,0.212,0.335)
同理:
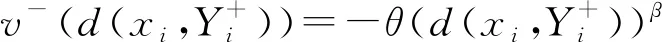
得到最佳理想融资方案前景价值矩阵W+:

得到最不利理想融资方案前景价值矩阵W-:

步骤5将上述前景价值矩阵W+与W-及式(7)~(8)代入目标函数(13),价值及权重函数参数取值说明:由于缺乏实验数据,根据过往文献[14-15]的参数取值适用于交通领域基于前景理论的方案决策,故本文取值分别为:γ=0.61,δ=0.69,α=0.88,β=0.88,θ=2.25,代入以上参数,求解非线性规划目标函数模型,可以得到具体属性指标权重值.
(0.023 3,0.201 4,0.207 6,0.157 6,0.027 5,
0.043 3,0.101 7,0.106 9,0.100 3,0.030 4)
步骤6利用加权算数平均算子集成决策矩阵Ak=(αij)n×m的第i行的所有元素,从而得到各融资方案的区间直觉模糊值.
步骤7利用得分函数与精确函数对αi进行排序
δ(α1)=0.299 4,δ(α2)=0.366 2
δ(α3)=0.270 2,δ(α4)=0.223 9
对应的四种投融资方式排序为:x2>x1>x3>x4,因此,最佳投融资方式为x2流域综合开发,其包括砂石特许经营、沿线土地租赁等模式.
4 比较分析
如果该项目为高等级航道项目,同理,可得到各融资方案的区间直觉模糊值.
利用得分函数与精确函数对αi进行排序
δ(α1)=0.268 4,δ(α2)=0.286 2,
δ(α3)=0.233 9,δ(α4)=0.327 4
对应的四种投融资模式排序为:x4>x2>x1>x3,因此,最佳投融资方式为x4其他(银行贷款、发行债券).可以看出由于不同类型的航道PPP项目对区域经济的影响和贡献不同,对评价指标权重的限制不同,导致投融资模式决策存在一定差异.
5 结 束 语
当前对于航道PPP项目投融资方案的决策,主要依赖于专家和政府部门的专业能力和经验判断,没有考虑到评价指标的适用性与模糊性.传统的多属性决策方法对于指标权重的确定多针对评价指标属性的考量,如层次分析法、组合赋权法、模糊熵等,而没有从项目本身特征和决策者自身心理活动考虑.本研究考虑了不同等级航道对社会的影响和贡献,将基于区间直觉模糊集的多属性决策方法拓展运用到航道PPP项目投融资决策中,以国际通行的PPP项目评估标准物有所值(VFM)为依据,构建了专用的评价指标体系和指标权重范围.引入前景理论充分考虑到当决策者面对投融资方案所带来的收益与损失会表现出不同的敏感性,选取两种极端形式的参照点,用区间直觉模糊集的距离公式测度到参考点的距离.以各融资方案的综合前景值最大化为目标函数,求得全局最优权重,进而得到各融资方案的区间直觉模糊值并进行科学排序.本研究进一步丰富和拓展了区间直觉模糊集多属性决策的应用范围,为航道PPP项目投融资决策提供了新思路.
